航空声纳浮标多基地探测阵型性能分析*

杜向辉 王永恒 刘 亭

（1.海装武汉局 武汉 430064）（2.中国航空工业集团公司洛阳电光设备研究所 洛阳 471009）

1 引言

航空反潜具有反应速度快、搜潜效率高、攻潜效果好的特点，在反潜战中发挥着重要作用。航空平台与水面舰艇、潜艇等其他搜潜装备配合使用能够有效提高海军搜攻潜效能。目前，现代新型安静型潜艇的噪声级已降低至海洋环境噪声级的水平，未来必将不断增强自身“隐、快、多、小”的声隐身特性［1～3］。为了有效探测水下目标，基于传统单传感器有人平台的探测方式正朝着多基地、多平台和无人化的方向发展。国外海军已经开始向无人平台为中心的反潜战概念发展，重点增加了无人反潜战传感器和平台的投资［4～6］。

航空声纳浮标采用多基地探测方式可以很好地应用于未来无人化航空平台中，利用其优异的灵活性、良好的隐蔽性和丰富的目标信息可以有效探测潜艇、UUV等水下目标，达到威慑敌方目标，掌握战场态势，占据战场主动权的目的。

国外无人机平台结合航空声纳完成潜艇探测的代表为英国超级电子（Ultra Electronics）公司。在公开发表的资料中，其新型反潜作战模式通常以作战决策中心为核心，首先通过侦查情报得到敌方目标的可能位置，然后启用无人机携带多枚航空声纳浮标在指定区域进行部署，实现对水下目标的探测、定位和跟踪，最终利用有人或者无人平台完成对目标的精确打击。

针对反潜巡逻机应召搜潜实际使用中面临的问题，国内相关学者和专家重点对多基地声纳浮标布阵模型及其搜潜效能进行分析和研究，主要涉及探测阵型设计，包括线形阵、圆形阵、方形阵、弧形阵和三角阵等；布阵算法及其优化；搜潜概率模型建立等内容［7～11］。上述发表的论文中，针对确定浮标阵型下的声学探测性能分析论述相对偏少。本文针对航空声纳浮标的多基地探测阵型的声学性能进行论述分析，主要涉及探测面积和定位误差。

2 无人机多基地浮标探测阵型

国内相关学者研究的浮标布阵阵型多集中于线形阵、圆形阵、方形阵、弧形阵和三角阵，但是航空平台（如直升机、无人机、巡逻机）在实际使用中由于飞机速度高，当采用圆形阵、弧形阵等特殊阵型进行布放时，给飞行员的航路控制会带来一定的不便，且这些探测阵型并未针对浮标多基地探测模式进行过优化设计，因此有必要参考和借鉴国外的多基地浮标探测阵型，通过对其仿真分析，得到其理论上的声学探测性能。

2.1 “田字格”探测阵型

近年来，英国超级电子公司的无人机浮标采用“田字格”探测阵型完成对指定区域的水下目标拦截、探测和定位，其阵型示意图如图1所示，其中圆圈代表接收浮标，星形代表发射浮标。根据其无人机自身的浮标携带能力，本探测阵型共包含21枚接收浮标和3枚发射浮标，其最小接收阵型为“田字格”形式，即1枚发射浮标和9接收浮标，发射浮标和中心的1枚接收浮标位置相同。从平台使用投放的角度来看，该阵型等同于3条平行的直线阵，飞机平台不会涉及复杂的航路规划和飞行操作，因此有利于实际应用，确保了执行效率。

图1 “田字格”探测阵型示意图

2.2 “十字”探测阵型

从图1所示的探测阵型可知，一次探测任务的最小探测单元为10枚浮标，如果该区域没有目标，则会造成浮标费用的增加，而且会浪费飞机平台的总任务时间。因此，从提高探测效率和降低运行成本的角度考虑，本文将上述阵型进行一定方式简化，即将最小探测单元进行简化为1声源浮标和5接收浮标的“十字”形式，其示意图如图2所示，其中圆圈代表接收浮标，星形代表发射浮标。暂不考虑探测性能，图2所示的探测阵型相比图1可以减少10枚接收浮标，因此可以有效节省探测成本。

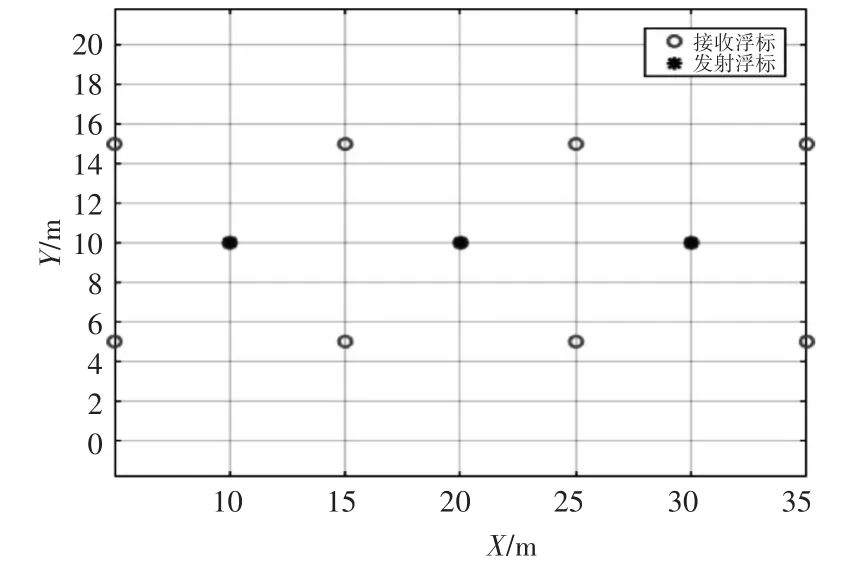
图2 “十字”探测阵型示意图

为了定量分析“十字”探测阵型和“田字格”探测阵型在探测性能的差异，需要对两种布放阵型的探测范围和定位误差进行建模和仿真分析。

3 不同阵型探测面积分析

3.1 多基地探测面积分析方法

由于多基地的探测定位范围可以看作是多个双基地探测范围的并集，因此需要对双基地的探测定位范围进行分析。

根据主动声纳方程，双基地声纳的声纳方程如下：

其中，SL双为发射声源级；TS为目标强度；TLTS为信号从发射机到目标的传播损失；TLSR为信号从目标到接收机的传播损失；NL为环境噪声谱级；GS为接收空间增益；GT为处理时间增益；DT为系统检测阈。

将上式变形如下：

在此忽略海水声吸收系数α对传播损失的影响，故公式进一步简化：

其中：rT为发射站到目标的距离；rR为目标到接收站的距离；R2=10(SL双+TS-NL+GS+GT-DT)/15是常数，该数值由声纳系统参数来确定。

查阅数学手册可知，方程（3）为卡西尼卵形线的定义式。一般定义为双基地浮标系统的等效半径。因此双基地声纳的探测区域为由发射站和接收站为焦点的卡西尼卵形线所包围的区域，而多基地探测范围则是全部双基地覆盖范围的并集。

对于卡西尼卵形线，其形状与焦点间距D（基线长度）相关。图3给出了双基地声纳系统等效作用距离R=10km时，不同基线长度下双基地声纳探测范围曲线，即发射站位置不变，调整接收站位置。从图中可以看出：当发射站位置固定时，随着基线长度D的增大，整个探测范围向接收站的方向扩展。但是随着D的增大，整个探测范围在基线轴垂直方向上产生压缩，即探测的范围在减小。当基线长度大于2被作用范围时，双基地的探测范围退化为两个独立的区域。因此在进行多基地布阵时，需要根据浮标探测范围合理设计基阵形状和位置。

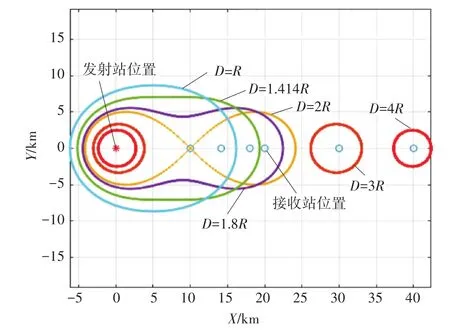
图3 双基地声纳在R不变，不同基线长度D下的探测范围

结合上一节中的探测阵型，选用两种基线长度，即D=R和D=1.414R，对探测性能进行仿真。其中“田字格”仅有一种阵型，“十字”探测阵型有D=R和D=1.414R两种探测阵型。

3.2 不同探测阵型的探测面积仿真分析

3.2.1 “田字格”探测阵型的探测面积

“田字格”阵型中每个子单元中心的声源浮标与周围9枚接收浮标分别组成双基地，其每个双基地的探测范围如图4（a）所示，发射浮标与接收浮标的布放间距分别为D=0、D=R和D=1.414R三种。整个探测阵型共包含三个子探测单元，分别由红色、粉色和黑色曲线表示。“田字格”整体的探测范围是由全部双基地探测范围的并集组成，具体探测范围的黑白图如图4（b）所示。

图4 “田字格”探测阵型探测面积示意图

3.2.2 “十字”探测阵型的探测面积

“十字”阵型中每个子单元中心的声源浮标与周围5枚接收浮标分别组成双基地，发射浮标与接收浮标的布放间距分别为D=0和D=1.414R，整个探测阵型共包含三个子探测单元，分别由红色、粉色和黑色曲线表示，其每个双基地的探测范围如图5（a）所示。“十字”阵型整体的探测范围是由全部双基地探测范围的并集组成，具体探测范围的黑白图如图5（b）所示。当发射浮标与接收浮标的布放间距分别为D=0、D=R时，整体探测范围图如图6所示。

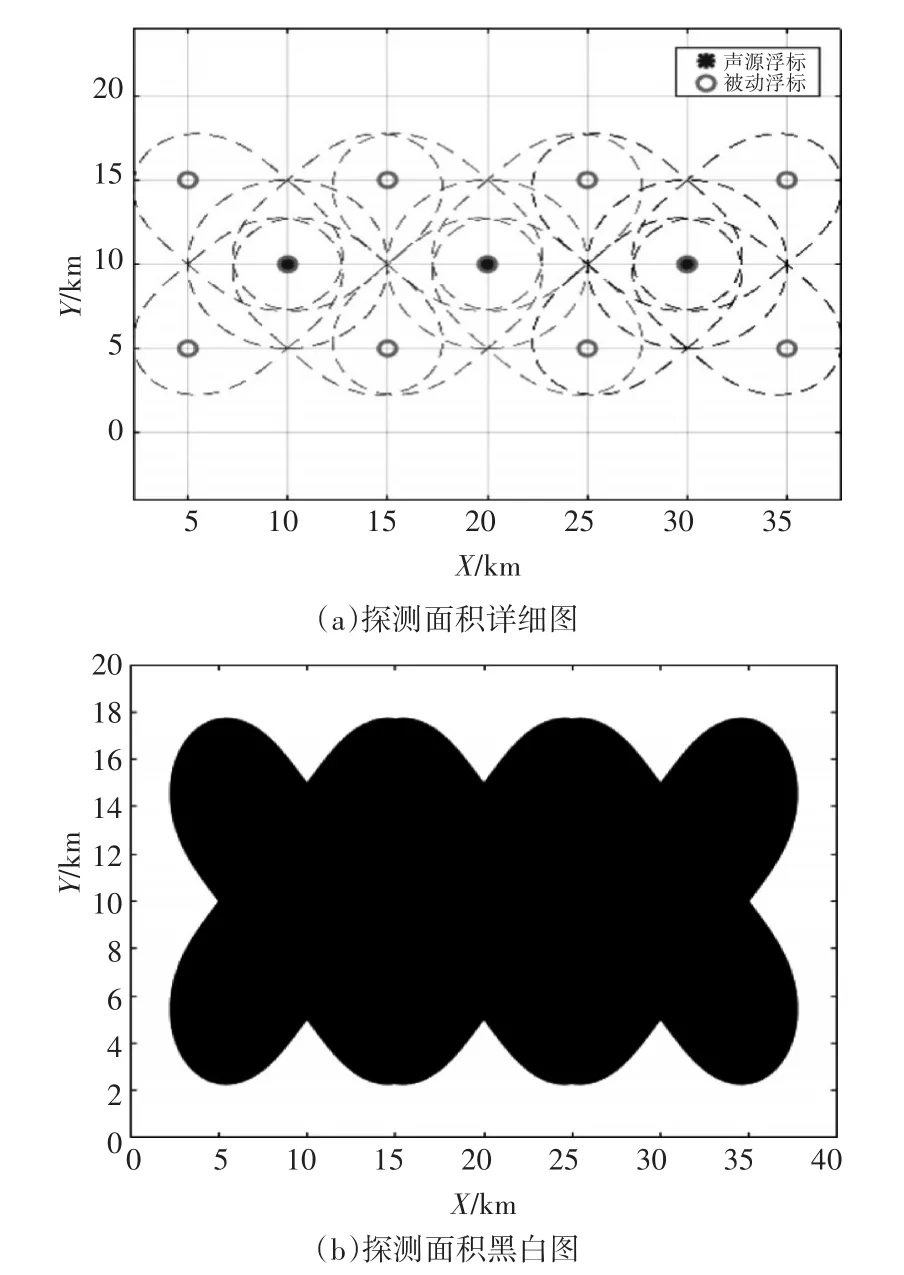
图5 “十字”探测阵型Ⅰ探测面积示意图

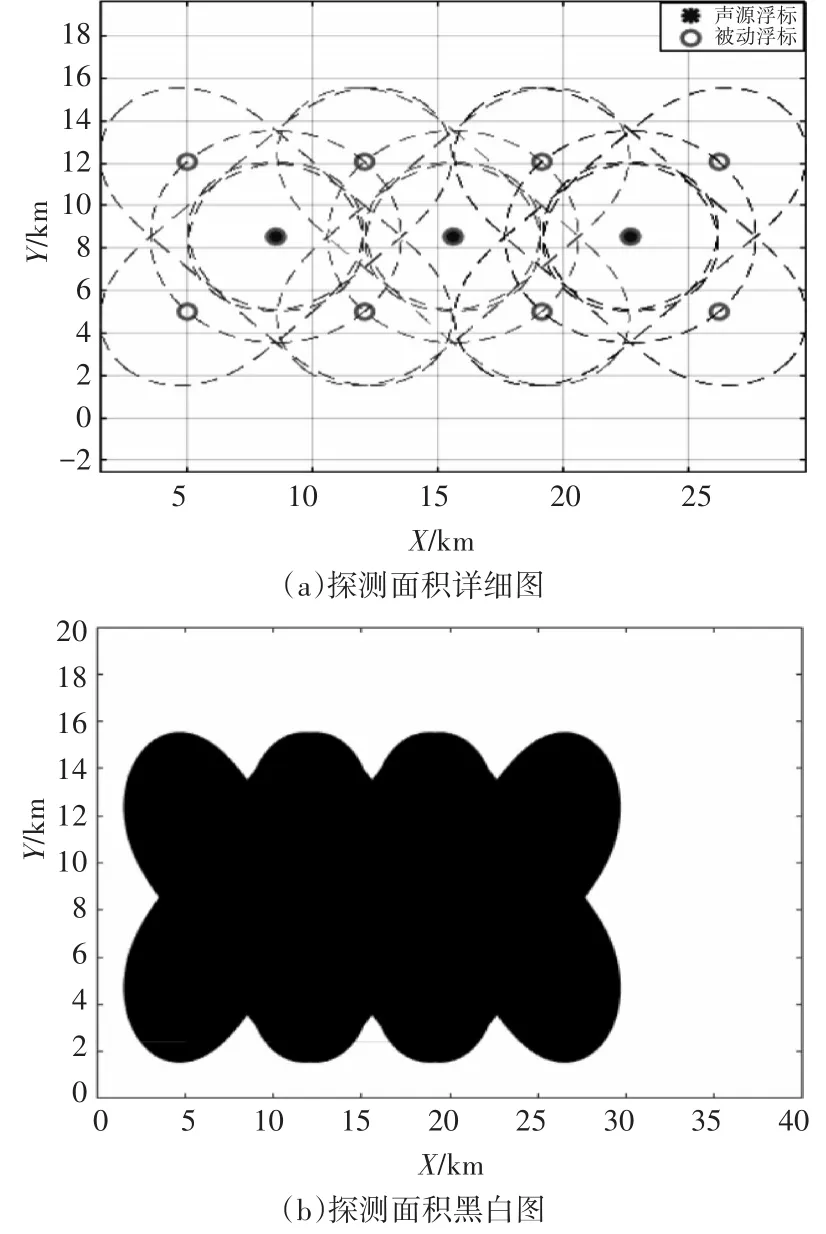
图6 “十字”探测阵型Ⅱ探测面积示意图

3.2.3 小结

仿真中多基地浮标中声源浮标与接收浮标的等效作用距离R为5km，按照“田字格”探测阵型、“十字”探测阵型Ⅰ和“十字”探测阵型Ⅱ计算得到的探测面积为534.755km2、470.1675km2和348.1450km2。将计算结果与作用距离半径建立关系，得到表1的计算结果。从归一化探测面积结果可知：“十字”探测阵型Ⅰ和“十字”探测阵型Ⅱ相比“田字格”探测阵型，其探测面积缩小至原始面积的87.92%和65.10%。

表1 不同阵型探测面积

4 不同阵型定位误差分析

本文重点关注T-Rn类型多基地声纳浮标系统，即一个声源浮标和n个被动定向浮标，其中声源浮标和被动定向浮标具有自身位置信息。图7给出的是T-R3多基地探测定位解算的坐标系示意图。其中，rΣi=rT+rRi为声源发射的信号进过目标散射后到达第i个被动定向浮标的总传播距离，θRi为每个被动定向浮标测量得到的目标角度。

图7 多基地声纳探测定位解算坐标系示意图

4.1 多基地定位误差分析方法

根据图7给出示意的坐标系，给出T-R3型多基地声纳浮标系统的定位解算原理。考虑到声纳作用距离通常要高出探测目标深度一个数量级以上，即目标的垂直向的俯仰角很小，故只在水平坐标内考虑定位。以发射站为原点建立二维直角坐标系，有如下的定位方程成立：

其中 i=1，2，3 xT=yT=0。

4.1.1 双基地解算算法

根据双基地的工作特点，利用三角形边长的余弦定理，可得如下方程：

在得到rRi之后，容易求得在双基地探测方式下的目标位置坐标为

4.1.2 平均算法

对于多基地定位解算最直接的算法是将各个双基地的目标位置解算结果进行平均处理，可以利用式（6）得到的各个双基地的解算结果进行平均处理得到最终的目标定位结果。

式中：x(i)、y(i)为第i个有效接收站方程的解，n为存在有效解的接收站数目。

4.1.3 基于数学变换的线性最小二乘算法

为了充分利用多个被动定向浮标存在的冗余信息，现采用最小二乘法来求解目标的定位问题，其实现原理为将测量方程进行一定的数学变换，消去二次项得到一组新的线性方程组。将式（4）消去二次项得到：

利用两个接收基站的测量结果消掉发射站到目标的距离，则有如下等式成立：

因此，可以得到如下线性方程组：

其中相关的系数矩阵如下：

现简化式（10）为EX=F，采用伪逆法完成对目标位置的估计，则有：

4.2 不同探测阵型的定位误差仿真分析

二维多基地声纳系统的目标定位误差可以用定位误差的几何解释（Geometrical Dilution of Precision，GDOP）来表示，即。其中，分别为二维笛卡尔坐标系内x方向和 y方向的目标定位解算位置方差。对于上一节分析的三种阵型，假定相邻发射声源之间不会产生声学影响，定位误差的分析可以直接分析各自探测阵型其最小探测单元的定位误差。

仿真条件：双基地探测距离5km，测向精度5°，测距精度为112.5m，仿真的距离间隔0.1km，蒙特卡洛次数500次，采用最小二乘算法进行多浮标下的水下目标定位解算。

4.2.1 “田字格”探测阵型的定位误差

图8给出的是“田字格”探测阵型中的最小单元的整体探测范围、定位误差三维图以及误差数据的统计分布结果。结合图 8（a）和图8（b）可知：探测范围中双基地覆盖范围最多的区域定位误差最低，图8（b）中四个角存在定位盲区（黄色区域），主要是由于此时系统只能按照双基地模式进行目标的定位解算，因此在发射浮标和接收浮标的连线出存在一定范围的定位盲区。

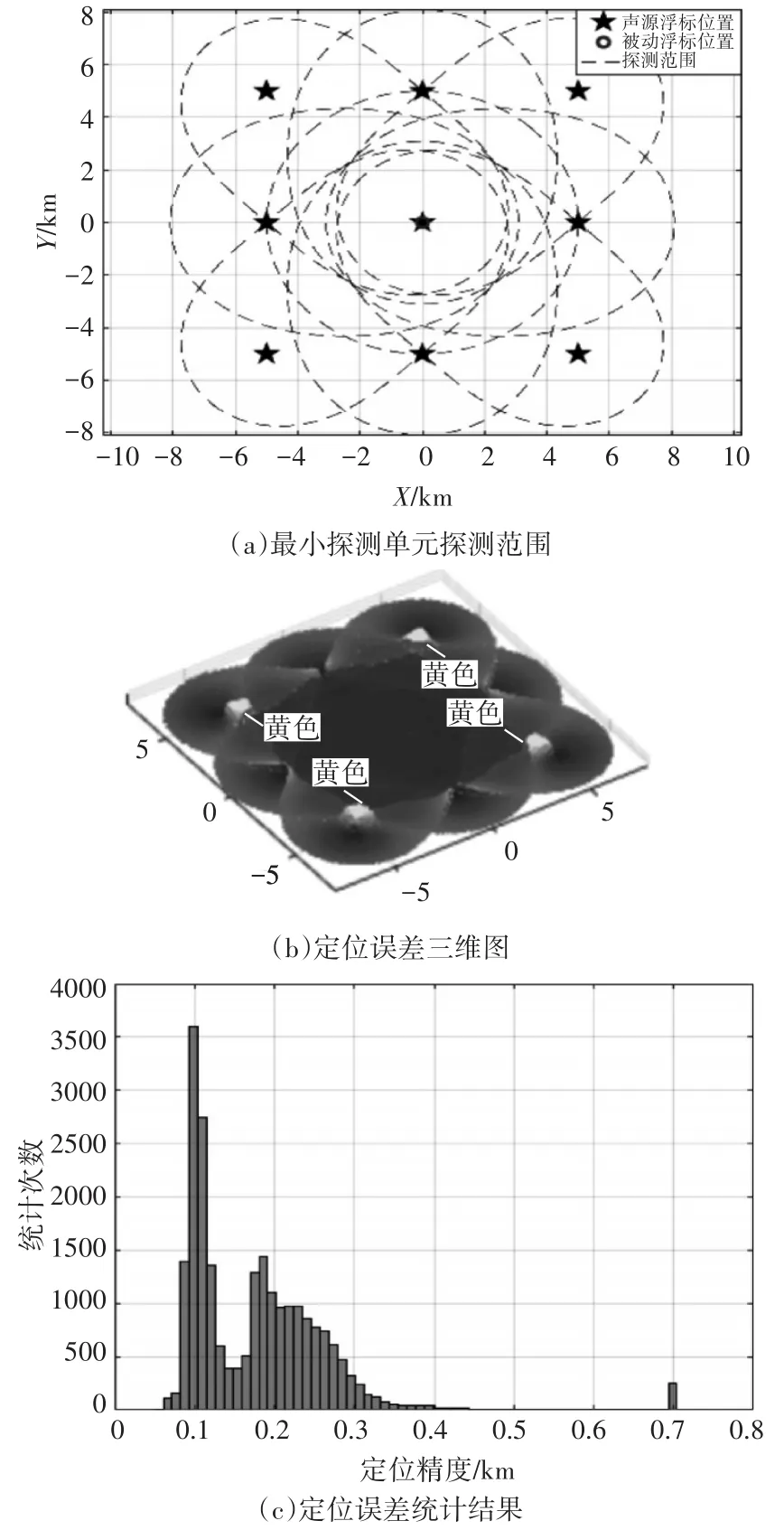
图8 “田字格”探测阵型定位误差结果

4.2.2 “十字”探测阵型Ⅰ的定位误差

“十字”探测阵型Ⅰ（D=1.414R）的探测定位误差如图9所示。相比于“田字格”探测阵型，由于参与定位解算的浮标数量减少了10枚，其定位解算的冗余信息减少了4个距离信息和4个方位信息，因此定位结果中盲区的面积有所扩大，相同位置的定位误差有一定降低，具体数值如图9（c）所示。

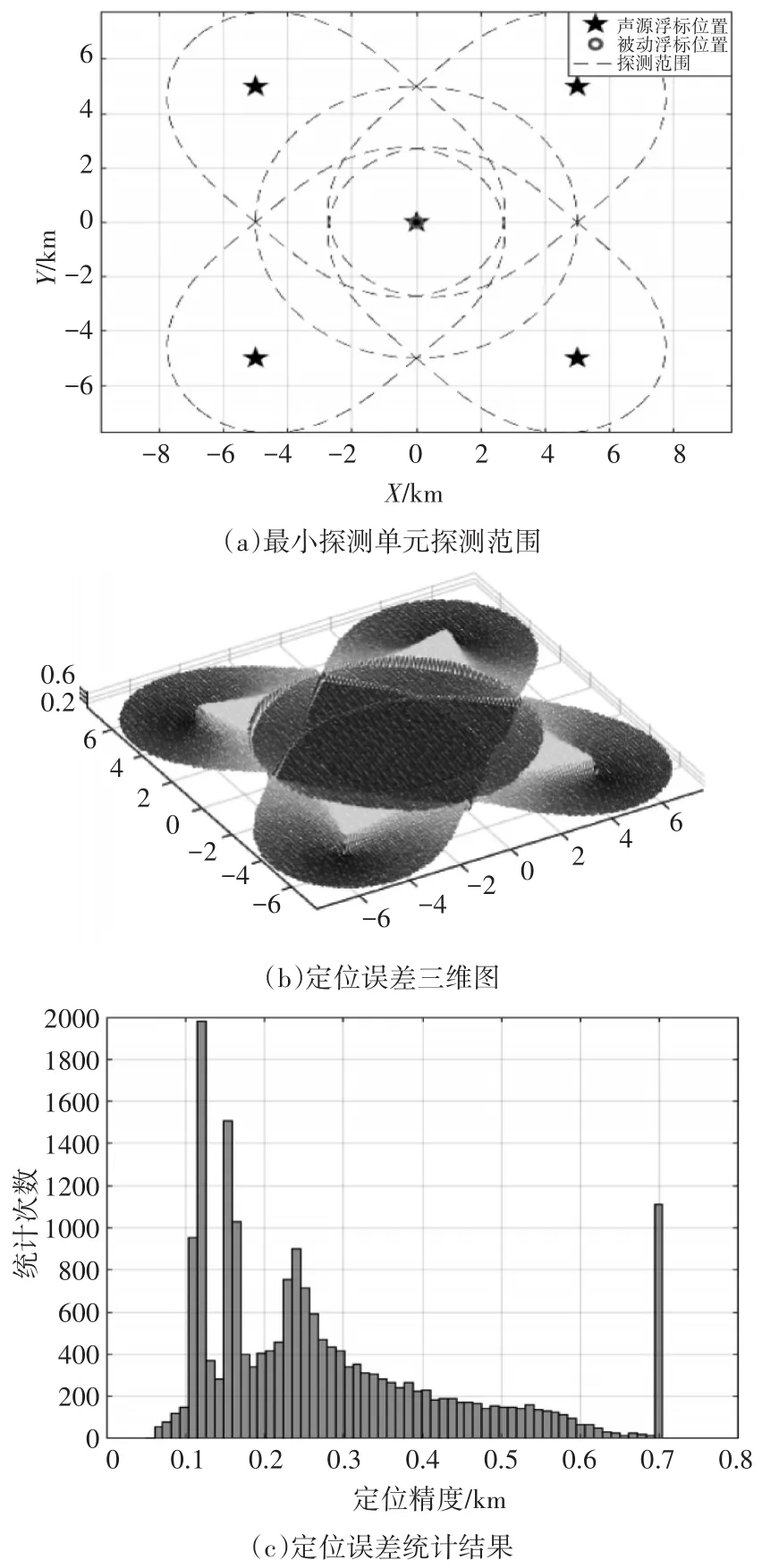
图9 “十字”探测阵型Ⅰ定位误差结果

4.2.3 十字”探测阵型Ⅱ的定位误差

“十字”探测阵型Ⅱ（D=R）的探测定位误差如图10所示。相比于“十字”探测阵型Ⅰ，本探测阵型使用的浮标数量相同，但定位误差盲区已经消失，其原因是由于中心接受浮标与发射浮标组成的双基地定位信息有效避免了定位盲区，具体数值如图10（c）所示。当然，该探测阵型是以牺牲探测面积来换取定位误差的改善。

图10 “十字”探测阵型Ⅱ定位误差结果

4.2.4 小结

对上述三种阵型得到的定位误差仿真数据按照100m误差间隔进行统计，具体结果如表2所示。从数据统计结果可知：“田字格”探测阵型的定位误差性能优于“十字”探测阵型Ⅰ优于“十字”探测阵型Ⅱ。

表2 不同探测阵型的定位误差统计结果对比

5 结语

本文给出了两种常用的航空声纳浮标多基地探测阵型，即“田字格”探测阵型和“十字”探测阵型，两种阵型的探测性能对比如表3所示。在固定的探测范围下，“田字格”探测阵型可以得到最大的探测面积和最优的定位误差，但消耗的浮标数量最多；“十字”探测阵型Ⅰ相比“田字格”探测阵型，探测面积浮标数量减少10枚，探测面积减少为87.92%，定位误差升高；“十字”探测阵型Ⅱ相比“田字格”探测阵型，探测面积浮标数量减少10枚，探测面积减少为65.10%，定位误差升高但要优于“十字”探测阵型Ⅰ。

表3 不同探测阵型下探测性能对比

在航空声纳浮标进行多基地探测时，可以首先采用“十字”探测阵型对水下目标进行初步探测；当探测到水下目标，需要进行精确打击时，航空平台可以补投浮标，形成“田字格”探测阵型，以此来提高对水下目标的打击命中率。