基于快速模糊聚类的动态多直方图均衡化算法

江巨浪，刘国明，朱 柱，黄 忠，郑江云

（安庆师范大学电子工程与智能制造学院,安徽安庆 246133）

1 引言

对比度增强技术被广泛用于改善图像视觉质量、提高机器视觉对图像关键特征的感知能力［1，2］.在对比度增强的各类方法中，直方图均衡化（Histogram Equalization，HE）因其简单性和有效性得到广泛应用.该方法利用图像直方图信息确定灰度级映射函数，通过自动拉伸图像动态范围获得较高对比度.传统HE算法容易导致过度扩展高频灰度级区间而产生过度增强，以及过度合并低频灰度级而引起细节丢失.同时，HE 算法的输出图像平均亮度是与原图像亮度无关的恒定值，容易导致图像真实感丢失与视觉效果不自然［3，4］.

针对HE 算法的过度增强与细节丢失问题，基于修改直方图的方法被提出［5］.该方法通过限制高频灰度级的压倒性优势，改善了图像中高频度灰度级所在区域的过度增强与低频度灰度级所在区域的细节丢失.由于修改后的直方图幅度受到限制，该方法在保留图像细节的同时也减弱了图像整体增强效果.为了解决这一矛盾，研究者们提出了多种不同策略以控制与平衡直方图中高频和低频灰度级的增强率［6～9］.多直方图均衡化是改进HE算法的另一种有效途径.该方法将图像直方图分割为多个子直方图，让图像增强在每个子直方图中独立进行，避免了高幅值子直方图对低幅值子直方图动态范围的过度压缩，达到避免过度增强与保持细节的目的.多直方图均衡化的另一个功能是在一定程度上保持了原图像亮度.双直方图均衡化方法最早被提出，在确定直方图分割阈值的策略上提出了一些典型算法，包括亮度保持的双直方图均衡化算法（Brightness preserving Bi-Histogram Equalization，BBHE）［10］、二元子图像直方图均衡化算法（Dualistic Sub-Image Histogram Equalization，DSIHE）［11］、最小平均亮度误差的双直方图均衡化算法（Minimum Mean Brightness Error Bi-Histogram Equalization，MMBEBHE）12］、基于阈值和优化的直方图均衡化算法（Thresholded and Optimized Histogram Equalization，TOHE）［13］、基于最大熵模型的双直方图均衡化算法（Maximum Entropy Model based Bi-Histogram Equalization，MEMBHE）［14］、基于模糊分割的双直方图均衡化算法（Fuzzy-based Histogram Partitioning for Bi-Histogram Equalization，FHPBHE）［15］.这些算法具有一定的图像亮度保持能力，在不同程度上改善了过度增强与细节丢失，比传统的HE 算法能够获得更自然的增强效果.基于进一步提高图像增强质量的需要，多直方图均衡化方法被提出.子直方图数量与分割阈值是多直方图均衡化的两个关键问题，对图像增强结果直接产生重要影响［16］.直方图分割数量越多，越有利于保留图像亮度以及图像局部细节，但太多的子直方图使图像增强效果明显减弱.此外，如果分割直方图的阈值选择不当，会导致子直方图内部存在主导性灰度级成分，进而导致过度增强.目前，多直方图的分割阈值选择方法大体可分为两类.一类方法是由用户指定子直方图分割数量，其中的典型算法包括递归均值分割的直方图均衡化算法（Recursive Mean Separate Histogram Equalization，RMSHE）［17］、递归的子图像直方图均衡化算法（Recursive Sub-Image Histogram Equalization，RSIHE）［18］、递归分割与加权的直方图均衡化算法（Recursively Separated and Weighted Histogram Equalization，RSWHE）［19］、基于图像聚类的多直方图均衡化算法［20］.在这些算法中，没有对直方图分割数量提出一个最优的选择方案，需要用户自行选择.另一类方法能够自动确定直方图分割的数量，典型算法包括四元动态直方图均衡化算法（Quadrants Dynamic Histogram Equalization，QDHE）［21］、动态直方图均衡化算法（Dynamic Histogram Equalization，DHE）［22］、基于熵的动态子直方图均衡化算法（Entropy-based Dynamic Sub-Histogram Equalization，EDSHE）［23］、基于曝光区域的多重直方图均衡化算法（Exposure Region-based Multi-Histogram Equalization，ERMHE）［24］.

多直方图均衡化方法通过对直方图分割与独立的均衡化处理，显著改善了高值直方图区域的过度增强与低值直方图区域的细节退化.然而，现有的多直方图均衡化算法尽管对于某些特定类型的图像取得了令人满意的效果，但仍然缺乏对不同亮度特征的图像的普适性.对此，本文提出一种基于快速模糊聚类的动态多直方图均衡化算法.通过采用直方图加权的模糊C-均值聚类（Fuzzy C-Means，FCM）与最优Davies-Bouldin Index（DBI）标度量方法，实现对直方图的快速自动分割.在子直方图均衡化过程中，综合运用直方图裁剪与动态范围分配方法，避免直方图均衡化引起的过度增强与细节退化.通过与现有同类算法的性能比较，验证该算法在处理不同亮度图像时的整体性能的优越性.

2 算法描述

2.1 直方图分割

采用图像聚类方法，将原图像分割为若干子图像，并依据每个子图像的灰度区间对图像直方图进行分割.使用DBI指数作为聚类质量好坏的评价指标，以确定最佳聚类个数.

2.1.1 基于直方图加权的FCM快速聚类

FCM 作为一种无监督聚类算法，在图像聚类中得到广泛应用［25］.采用FCM 算法对图像进行聚类时，如果将所有像素灰度值直接作为数据样本将会使聚类过程十分耗时，且运行时间随图像尺寸增大而急剧增加.本文将图像的所有灰度级及其频度共同作为待聚类的数据样本，构造一种基于直方图加权的FCM 图像快速聚类算法.由于样本数目是一个与图像尺寸无关的常向量（即数字图像常用的256 个灰度级），算法效率得到大幅度提升，并且完全不受图像尺寸增加的影响.令数据样本为图像X的所有灰度级构成的向量G={G1,G2,…,Gn}，图像灰度直方图为h={h1,h2,…,hn}，其中n=256.令图像聚类个数为c，聚类中心为V={V1,V2,…,Vc}.用一个n×c的矩阵U=[μi,j]n×c描述聚类结果.其中μi,j∈[0,1]，表示第i个样本Gi属于第j类的隶属度.对于∀i，有=1；对 于∀j，有1 ＜.基于直方图加权的FCM 算法通过迭代运算对以下目标函数进行优化：

该目标函数在传统FCM 算法基础上增加了一个基于灰度直方图h的权重因子.b为模糊指数，通常取值为2.令f分别对μi,j与Vj的偏导数为0，可获得使目标函数为极小值的优化迭代公式.

采用直方图加权的FCM 快速聚类算法，将图像分割为c类，具体步骤如下.

Step1输入图像，计算直方图h，令G={0,1,2,…,255}.

Step2输入聚类数c.设定迭代停止阈值ε.

Step3令迭代次数k=1.用随机值初始化矩阵U(k)，用式（2）计算聚类中心V(k)，用式（1）计算目标函数f(k).

Step4k=k+1.用式（3）计算矩阵U(k+1)，用式（2）计算聚类中心V(k+1).

Step5若‖V(k+1)-V(k)‖＜ε，则迭代过程结束.否则，返回Step4.

Step6按照最大隶属度原则确定样本G中的每个灰度级所属类别.根据灰度值对图像像素进行分类.

2.1.2 图像聚类个数的选择

聚类个数的合理选择，是获得高质量图像聚类结果、提高直方图分割合理性的关键.本文采取遍历不同聚类个数的方式，选择对应于最优图像聚类质量的聚类个数.考虑算法效率与便捷性，选择DBI作为图像聚类质量评价指标［26］.DBI基于类内散度与类间距离的综合度量对聚类质量进行评价，其数值越小表明聚类质量越好.DBI的计算式如下：

式（4）中，DWi为第i类的所有样本到其聚类中心的平均距离，DCij为第i类中心到第j类中心的距离.通过遍历不同聚类个数并计算对应的DBI值，从中选择对应于最小DBI的聚类个数，作为最佳聚类个数c.将c值的遍历范围设为2～6，采用基于直方图加权的FCM算法对图像girl 进行聚类与直方图分割（图1），表1 记录了不同聚类个数对应的DBI 值.数据显示，c=3 对应于最小的DBI 值，表明其对应于图像girl 的最优聚类结果.此时，在图1（c）中原图像像素被大致划分为3个类别：深色的头发与领结；灰色的脸部、衣服与背景；相对较亮的衣领.由最小DBI确定的最佳c值对应于相对合理的聚类结果，最佳c值通常随图像不同而改变.

表1 图像聚类个数c与对应的DBI值

图1 对应于不同c值的图像聚类及直方图分割

2.2 子直方图裁剪与动态范围分配

使用修改直方图方法，可以控制子直方图均衡化的增强率，以有效避免子图像的过度增强与细节退化.本文参考BHEPL 算法［8］，采用子直方图均值作为幅度极限对子直方图进行裁剪.对于第i个子直方图hi，假设其灰度级区间为[Gi1,Gi2]，幅度极值Ti的计算公式为

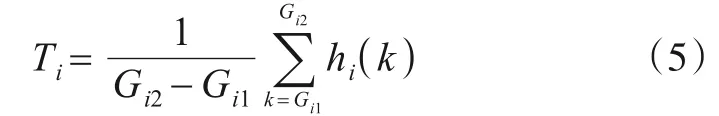
式（5）中，k为灰度级，k∈[Gi1,Gi2].通过裁剪，使子直方图hi中小于Ti的部分得到保留，大于Ti的部分被限幅.裁剪后的子直方图为，则

对于每个子直方图，根据其原有灰度范围与像素占比分配新的动态范围.对于子直方图hi，动态范围spani=Gi2-Gi1+1，采用下式计算hi在输出图像中的动态范围：

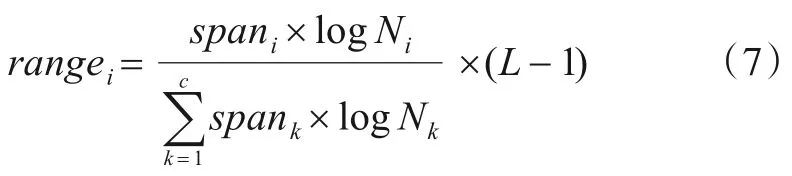
式（7）中，L为图像灰度级个数.Nk表示第k个子直方图包含的像素数量.一方面，式（7）使幅值较大的子直方图的动态范围在输出图像中得到放大，以确保图像主体部分的对比度有更明显的增强；另一方面，又通过引入对数运算使这种放大作用受到限制，以避免图像中非主体部分的细节退化.

2.3 整体算法描述

本小节描述了基于模糊聚类的动态多直方图均衡化算法，并将其命名为FCDMHE（Fuzzy Clustering based Dynamic Multi-Histogram Equalization）算法.首先遍历不同取值的聚类个数c（本文设置为2～6），对图像进行FCM 快速聚类，并根据聚类结果的DBI 值最小原则确定最佳聚类个数.然后依据子图像的灰度区间对图像直方图进行分割.对每个子图像，在完成直方图裁剪之后再进行独立的直方图均衡化处理，并映射到新的灰度级动态范围.最后合并所有子图像的直方图均衡化结果，得到输出图像.FCDMHE算法描述如下.

3 实验结果与分析

图2 是用于算法性能测试的8 幅图像.为了考察FCDMHE 算法对不同图像亮度特征的适应性，测试图像包括中等亮度图像girl 与logic IC、低亮度图像butterfly 与airplane U2、高亮度图像penguin 与aerial、亮度不均匀图像street 与moon.在图2 的每幅图像下方绘制了FCDMHE算法对图像直方图的分割结果.可以看出，对应于最优DBI的图像聚类个数（即直方图分割的数量c）不是一个固定的值，随图像不同而变化.在现有直方图均衡化算法中，选择较为典型的HE，RMSHE［17］，RSWHE［19］，DHE［22］，EDSHE［23］和FHPHE［15］算法，与FCDMHE 算法进行图像增强结果比较.其中，HE 算法不对直方图进行分割；FHPHE 算法的子直方图个数c=2；RMSHE 与RSWHE 算法的递归深度r由用户选择，在此选择为r=2，即c=4；DHE、EDSHE 与FCDMHE 算法的c值都是根据具体图像计算确定的，随图像不同而变化.在对比算法的实验中，HE 算法采用开源代码，RMSHE、RSWHE 与EDSHE 算法代码由本文依据原文献算法复现，DHE 与FHPHE 算法代码由文献作者提供.

下文从以下3 个方面对算法性能进行评价：（1）基于视觉效果的主观评价；（2）基于性能指标的客观评价；（3）算法运行时间.

3.1 主观评价

为了从视觉效果上验证FCDMHE 算法对不同图像亮度特征的适应性，在图2 中选择具有不同亮度特征的4 幅测试图像，采用不同算法得到的增强结果见图3～6.图3 是对中等亮度图像girl 的增强结果.HE和FHPHE 算法在人物面部、衣服上产生了过度增强，在背景区域产生了明显噪声.DHE 算法增强的人物面部失真，背景存在可见的噪声.RMSHE，RSWHE 与FCDMHE 算法都获得了较为自然的增强效果.图4 显示了不同算法对亮度偏低且动态范围小的图像butterfly 的增强结果.RSWHE 算法的增强效果不明显；RMSHE 算法增强的画面背景出现不自然的人工痕迹；HE和FHPHE 算法使花朵与背景产生了不同程度的过度增强，并且在蝴蝶左侧翅膀的偏暗区域丢失纹理；DHE、EDSHE 与FCDMHE 算法使画面中的蝴蝶翅膀、花朵与背景都获得了适度增强，视觉质量较好.图5 显示了高亮度图像penguin 的增强结果.HE 与FHPHE 算法产生了过于强烈的明暗变化与不自然的视觉效果；DHE 算法的图像亮度整体偏暗；RMSHE，RSWHE 与EDSHE 算法对于企鹅腹部与雪地的纹理没有明显的增强效果；观察FCDMHE 算法增强的图像，企鹅的腹部轮廓、腹部绒毛、雪地纹理都得到了适度增强，没有出现不自然的人工痕迹.图6 是对亮度不均匀图像street 的增强结果，原图像中左侧的背光建筑物与右侧明亮天空形成强烈的亮度反差.图像增强结果表明，只有FCDMHE 算法使建筑物的门柱轮廓变得清晰可见，增强效果优于其他算法.

图2 用于算法性能测试的8幅图像

图3 中等亮度图像girl的对比度增强结果

图4 低亮度图像butterfly的对比度增强结果

图5 高亮度图像penguin的对比度增强结果

图6 中等亮度图像street的对比度增强结果

图像增强的视觉效果表明，只有FCDMHE 算法在4 种亮度特征的图像增强中全部获得了较为理想的结果，而其他算法仅在部分测试图像上获得成功.FCDMHE 算法在有效增强图像细节的同时，没有出现过度增强导致的人工痕迹，处理的图像具有自然的视觉效果，对于各种亮度特征的图像具有较好的普适性.

3.2 客观评价

客观评价采用图像对比度、图像信息熵与NIQE（Natural Image Quality Evaluator）三种性能指标.

（1）图像对比度计算采用Wu给出的定义［27］，即

式（8）中，L为图像的灰度级个数；xi表示第i个灰度级；Pi是灰度级xi的分布概率.图像增强目的是适当提高对比度.图像增强后的对比度不是越大越好，因为过高的对比度往往对应于过度增强的结果.

（2）图像信息熵的计算式为

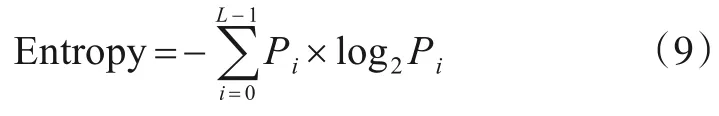
由于直方图均衡化会引起灰度级合并，图像信息熵随着灰度级个数减少而有所降低.图像增强后的信息熵越大，代表丢失的灰度级个数越少且图像细节保留越多.

（3）NIQE 是Mittal 等人提出的一种无参考图像质量评价指标［28］.该算法构造了一组“图像质量感知”特征并将它们拟合成一个多元高斯模型，利用待评价图像的特征模型参数与预先建立的模型参数之间的距离评估图像质量.NIQE 的值越小，代表图像质量越好.

采用不同算法对图2 的8 幅图像进行增强处理，将输出图像的3种性能参数分别统计于表2～表4.表的最后一行是处理所有图像的性能参数平均值.在表的每一行，对性能参数相对最好的3个数值使用了深色底纹与粗体字，用于突出显示相对较大的对比度与信息熵、相对较小的NIQE 值.从表2 数据看，HE 算法处理所有图像的对比度平均值最大，而视觉效果显示其容易产生过度增强；FCDMHE 算法增强图像的对比度值处在所有算法的中间位置，主观评价结果表明其对比度增强效果是适中的.表3 与表4 的数据显示，FCDMHE 算法处理每一幅图像的性能参数排名都位列所有算法的前3 名.该算法处理所有图像获得的平均信息熵最大，比位列第2、第3 名的RSWHE 与RMSHE 算法分别提高了0.20%与1.85%，表明其更好地保留了图像细节；该算法处理所有图像获得的平均NIQE 值最小，比位列第2、第3 名的RMSHE 与EDSHE 算法分别降低了2.38%与5.03%，表明其增强的图像视觉质量更高，视觉效果更自然.因此，客观性能指标表明，FCDMHE 算法对各种亮度特征的图像具有最好的普适性.

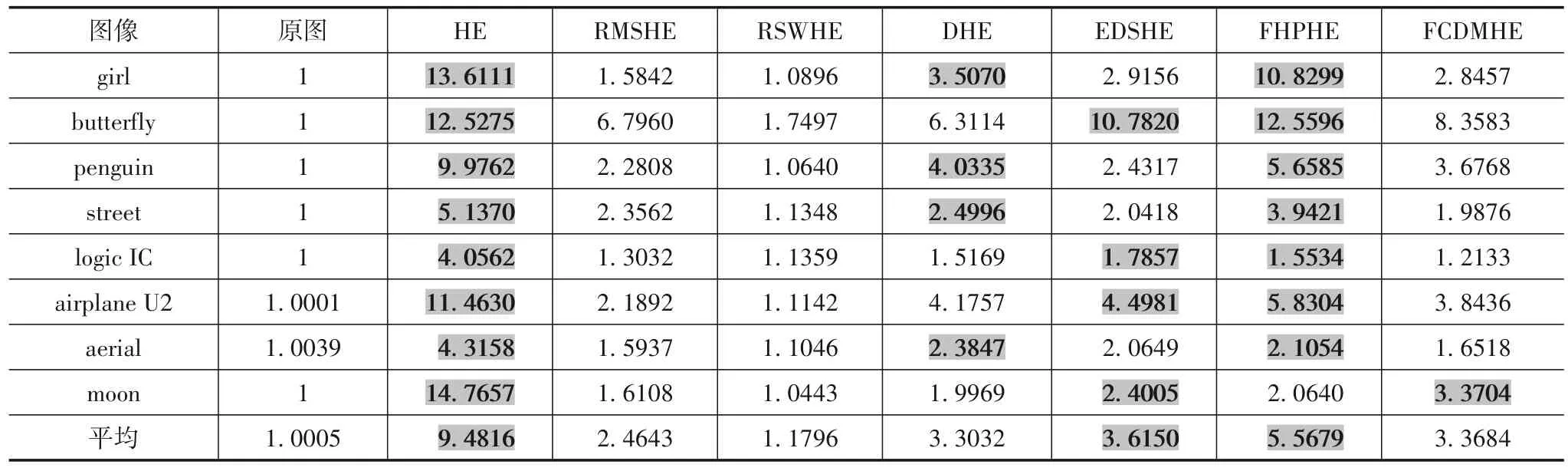
表2 图像对比度统计

表3 图像信息熵的统计

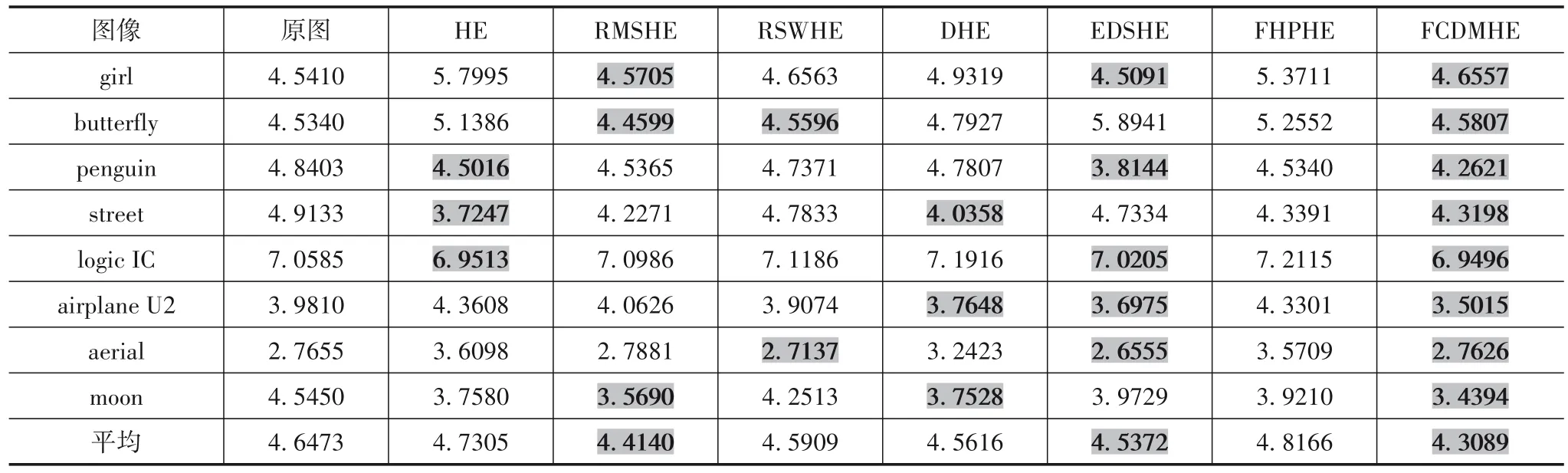
表4 图像NIQE的统计

3.3 算法运行时间

本实验中，采用MATLAB2016a 编程，CPU 为Intel Core（TM）i5-9400f，内存为4 GB，图像尺寸为512×512.在以上不同算法中，HE算法运行时间最短，为0.011 s；EDSHE 算法的运行时间最长，为0.3061 s.FCDMHE 算法运行时间为0.2806 s.由于该算法在遍历5 种聚类个数的图像聚类过程中，采用直方图加权的FCM 聚类算法极大加速了聚类过程，使其能够满足实时处理要求.

4 结论

由于现有的直方图均衡化算法对不同亮度图像的普适性不强，该文提出了一种基于图像聚类的动态多直方图均衡化算法.该算法基于图像聚类方法对直方图进行分割，图像聚类个数按照图像聚类质量评价指标的最优化原则确定.在子直方图均衡化过程中，综合运用直方图裁剪与动态范围分配方法，有效避免了过度增强与细节丢失.实验结果验证了上述措施的有效性，同时表明该算法适用于各种亮度特征的图像增强，能够获得较为稳定的视觉质量，算法效率满足实时要求.