几类最优重根循环码的构造

黄素娟，孙中华，朱士信

（1.合肥工业大学数学学院,安徽合肥 230601；2.智能互联系统安徽省实验室,安徽合肥 230009）

1 引言

循环码是一类重要的线性码，许多高效的纠错码都是循环码，如Golay 码和RS码等.重根循环码作为一类特殊的循环码受到广泛关注.Chen［1］在其博士论文中研究了码长为2n（n是奇数）的二元重根循环码的最小距离（相关结论亦可查阅文献［2］）.Gastagnoli 等人［3］证明了重根循环码的最小距离可以用一组单根循环码的最小距离来表示，并证明了重根循环码是渐进坏的.基于这一理论，编码学者们确定了几类重根循环码的最小距离（参阅文献［4～6］和它们的引用）.van Lint［7］通过(u|u+v)构造证明了码长为2n（n是奇数）的二元重根循环码可以通过两个码长为n的二元循环码来构造，并构造了参数为[2m-2，2m-m-3，4]的最优二元循环码.然而，由于重根循环码是渐进坏的，此后关于重根循环码最优性的讨论相对较少.

最新的研究结果表明，重根循环码在量子纠错码和符号对码的构造中有重要作用.以重根循环码为载体，文献［8～11］构造了几类参数优的量子重根循环码，文献［12］构造了几类参数好的非二元量子同步码.文献［13］和文献［14］，利用重根循环码的代数结构，确定了几类重根循环码的最小对距离，由此构造了几类有最大符号对距离的符号对码，从而说明重根循环码在符号对读信道上有较好的纠错能力.重根循环码的纠错能力是这两类应用中的一个关键点，因此，分析重根循环码的纠错能力并探讨它的最优性，是一个有趣的问题.

一个p元[n，k，d]线性码C称为距离最优的是指不存在参数为[n，k，≥d+1]的p元线性码.码C称为维数最优的是指不存在参数为[n，≥k+1，d]的p元线性码.本文基于循环码的代数的结构，首先，构造了几类最小距离是4 的距离最优二元重根循环码，特别地，其中一类距离最优码也是维数最优的线性码；其次，构造了一类最小距离是3 的距离和维数都是最优的非二元重根循环码；最后，构造了两类最小距离是4 的距离最优非二元循环码.本文的研究结果表明，重根循环码可以产生小距离的最优线性码.

2 预备知识

设p是一个素数，Fp是p阶有限域.设n是一个正整数，是Fp上n维行向量空间.的每个k维子空间称为一个码长为n且维数为k的p元线性码，记作[n，k].设x∈，向量x的Hamming 重量定义为x非零分量的个数，记作wt(x).设x，y∈，向量x和y的Hamming 距离定义为x-y的Hamming 重量，记作dist(x，y)，即dist(x，y)=wt(x-y).一个p元[n，k]线性码C的最小距离定义为

码长为n、维数为k和最小距离为d的p元线性码，记作[n，k，d].一个p元[n，k，d]线性码的三个参数满足球包界［15］：

对于p＞3元[n，k，d]线性码，文献［16］证明

一个码长n的p元线性码C称为循环码是指对任意 的(c0，c1，…，cn-1) ∈C，有(cn-1，c0，…，cn-2) ∈C.定义映射

则码长为n的p元线性码C是循环码当且仅当σ(C)={σ(c)|c ∈C}是商环R的理想.众所周知，商环R是主理想环，因此，对于每个码长为n的p元循环码C，存在唯一的多项式g(x) ∈Fp[x]使得g(x)|(xn-1) 且C=g(x)R=(g(x))，g(x)称为码C的生成多项式，并且码C的维数dim(C)=n-deg(g(x)).设n=peℓ，其中e和ℓ是非负整数且gcd(ℓ，p)=1.记ordℓ(p)为p模ℓ 的阶，即使得pl≡1(mod ℓ)的最小正整数.设ordℓ(p)=m，则在Fpm上存在一个ℓ次本原单位根α.设Zℓ=是整数模ℓ 的剩余类环.定义Zℓ上等价关系～：i～j⇔∃s∈Z，ips≡j(modn).用Λ表示等价类构成的集合，则

其中cl(i) 表示i所在的等价类.对于0 ≤i≤n-1，Fp[x]上以αi为根的次数最低首一多项式称作αi在Fp上的极小多项式.容易验证，αi在Fp上的极小多项式为(x-αj) ∈Fp[x].进一步可证，式（4）为xℓ-1 在Fp[x]上的不可约分解且xn-1=(xℓ-1)pe=当e=0 时，码长为n的p元循环码称为单根循环码；当e≥1 时，码长为n的p元循环码称为重根循环码.对于单根循环码的最小距离有如下著名的界［15］.

引理1设p是一个素数，n是一个正整数且gcd(n，p)=1.设α是一个n次本原单位根.设C是一个码长为n且生成多项式为g(x)的p元循环码.如果存在整数b，c1，c2且gcd(c1，n)=gcd(c2，n)=1使得

是g(x)的根，则码C的最小距离d(C) ≥δ+s.

当s=0 时，引理1 称为BCH 界.对于重根循环码的最小距离，Gastagnoli等人［3］提出了如下理论.

设xℓ-1 在Fp[x] 上的不可约分解为xℓ-1=m1(x)m2(x)…mr(x)，则码长为n的p元循环码C的生成多项式可唯一表示为g(x)=其中0 ≤si≤pe，i=1，2，…，r.对于0 ≤t≤pe-1，定义

引理2码长为n且生成多项式为g(x)=的p元重根循环码的最小距离d(C)=min{Pt·d()|0 ≤t≤pe-1}.

3 主要结果

基于重根循环码的代数结构，本节构造了几类最优码.

3.1 二元最优重根循环码

下面构造最优二元重根循环码.对任意的正整数ℓ，记v2(ℓ)表示ℓ 的2-进制展开中非零项的最高次幂，即如果v2(ℓ)=i，则ℓ 的2-进制展开为ℓ0+ℓ12+…+ℓi-12i-1+2i.

定理1设ℓ 是奇数且ℓ ≥3，e是正整数，则存在参数为[2eℓ，2eℓ-2e-1-ordℓ(2)-1，4]的二元重根循环码C(e，ℓ).当v2(ℓ2)-ordℓ(2) ≥2e-1-2e+2 时，C(e，ℓ)是距离最优的二元线性码.

证明设α是F2扩域上的ℓ次本原单位根，m(x)是α在F2上的极小多项式.设C(e，ℓ)是码长为n=2eℓ 且生成多项式为m(x)的二元重根循环码，则

首先，证明d(C(e，ℓ))=4.设是码长为ℓ 且生成多项式为(x+1)m(x)的二元循环码.因为α0，α1，α2是(x+1)m(x)的零点，由BCH 界，d()≥4.设是码长为ℓ且生成多项式为x+1的二元循环码，则d(Cˉ1)=2.容易验证P：=min{Pt：2e-1+1 ≤t≤2e-1}=4.由引理2，d(C(e，ℓ))=min{d()，2d()，P}=4.

最后，证明C(e，ℓ)的最优性.假设存在参数为[2eℓ，2eℓ-2e-1-ordℓ(2)-1，≥5] 的二元码，由球包界（1），

而不等式左端

矛盾.因此，C(e，ℓ)是距离最优的二元线性码.

注1定理1 的距离最优约束条件是充分的.通过计算机搜索，定理1可以产生39个码长不超过256的距离最优二元重根循环码，其中36 个码长满足定理1 中的约束条件，与码表［17］比较，36个距离最优二元码中有11 个码是维数最优的.详见表1.其中带#的码表示不满足约束条件的最优码，带*的码表示维数最优码.由此可以看出，尽管重根循环码是渐近坏的，但仍存在小距离的最优重根循环码.

表1 最小距离是4的最优二元重根循环码

由定理1，可以得到一系列最小距离是4 的最优二元线性码.下面给出几类具体的最优二元重根循环码.

推论1设m，e是正整数且m≥max{2e-1-2e+3，2}，则存在参数为[2m+e-2e，2m+e-3·2e-1-m-1，4]的距离最优二元重根循环码.特别地，当e∈{1，2}时，参数为[2m+e-2e，2m+e-3·2e-1-m-1，4]的二元重根循环码也是维数最优码.

证明设ℓ=2m-1，则v2(ℓ2)=2m-1且ordℓ(2)=m.由定理1，存在参数为[2m+e-2e，2m+e-3·2e-1-m-1，4]的距离最优二元重根循环码.

假设存在参数为[2m+e-2e，k≥2m+e-3·2e-1-m，4]的二元线性码.由界（2），1+n-1 ≤2n-k-1，即2m-1 ≤2n-1-e-k≤.当e∈{1，2} 时，m+2e-1-e-1=m-1，所以2m-1 ≤2m-1，矛盾.故参数为[2m+e-2e，2m+e-3·2e-1-m-1，4]的距离最优码也是维数最优码.

推论2设e是正整数，m是偶数且m≥2e-1-2e+6，则存在参数为

的距离最优二元重根循环码.

所以v2(ℓ2)=2m-4.由定理1，结论成立.

推论3设m是正偶数且e∈{1，2，3，4}，则存在参数为[3(2m+e+2e)，3·2m+e+5·2e-1-2m-1，4]的距离最优二元重根循环码.

证明设ℓ=3(2m+1)，则ordℓ(2)=2m且v2(ℓ2)=2m+3.当e∈{1，2，3，4}时，

由定理1，结论成立.

推论4设m≥3 是正奇数且e∈{1，2，3，4}，则存在参数为[3(2m+e-2e)，3·2m+e-7·2e-1-2m-1，4]的距离最优二元重根循环码.

证明设ℓ=3(2m-1)，则ordℓ(2)=2m.当m=3时，v2(ℓ2)=8；当m≥5 时，v2(ℓ2)=2m+3.容易验证，当e∈{1，2，3，4} 时，v2(ℓ2)-ordℓ(2) ≥2e-1-2e+2.由定理1，结论成立.

推论5设m是正整数且e∈{2，3}，则存在参数为[2m+e+2e，2m+e+2e-1-2m-1，4]的距离最优二元重根循环码.

证 明设 ℓ=2m+1，则 ordℓ(2)=2m且v2(ℓ2)=2m.当e∈{2，3}时，v2(ℓ2)-ordℓ(2) ≥2e-1-2e+2.由定理1，结论成立.

3.2 非二元最优循环码

本小节将构造几类非二元最优码.

定理2设p是一个奇素数，m是一个正整数，λ≥2且λ|(p-1)，则存在参数为

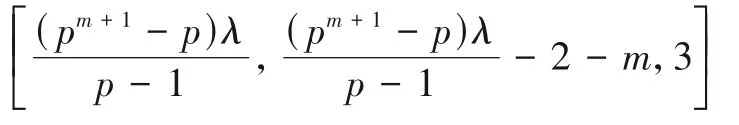
的距离和维数都是最优的p元重根循环码.

证明设ℓ=，α是Fp扩域上的ℓ 次本原单位根，m(x)是α在Fp上的极小多项式.设C是码长为n=pℓ 且生成多项式为(x-1)2m(x)的p元重根循环码，则dim(C)=n-2-m.

设是码长为ℓ 且生成多项式为(x-1)m(x)的p元循环码.因为α0和α1是(x-1)m(x)的零点，由BCH界，d()≥3.设是码长为ℓ且生成多项式为x-1的p元循环码，则d(Cˉ1)=2.容易验证，

下面讨论码C的最优性.由球包界（1）推出，不存在参数为[pℓ，pℓ-2-m，≥5]的p元线性码.假设存在参数为[pℓ，pℓ-2-m，4]的p元线性码，由界（3），1+(n-1)(p-1) ≤pn-1-dim(C)=pm+1，矛盾.因此，C是距离最优的p元循环码.同理，假设存在参数为[pℓ，k≥pℓ-1-m，3]的p元线性码，由球包界（1），1+n(p-1) ≤pn-k≤pm+1，矛盾.因此，码C是维数最优的p元循环码.

由定理2推出，存在如下最优的p元重根循环码.

推论6设p是一个奇素数且m是正整数，则

（i）存在参数为[pm+1-p，pm+1-p-2-m，3]的距离和维数都是最优的p元重根循环码；

（ii）存在参数为

的距离和维数都是最优的p元重根循环码；

（iii）如果p≥5，存在参数为

的距离和维数都是最优的p元重根循环码.

例1当p=3时，定理2构造了一类参数为[3m+1-3，3m+1-5-m，3]的最优三元循环码.对于短码长，表2给出了它们的生成多项式，与码表［17］比较，定理2 证明存在最优重根循环码.

表2 最小距离是3的最优三元重根循环码

例2当p=5时，定理2构造了两类最优五元循环码，它们的参数分别为[5m+1-5，5m+1-7-m，3]和对于短码长，表3 给出了它们的生成多项式，与码表［17］比较，定理2 证明存在最优重根循环码.

表3 最小距离是3的最优五元重根循环码

下面构造最小距离是4的最优p元循环码.

定理3设p是一个奇素数，m和n是正整数，n|(p2m-1)且n＞pm+1.设gcd(pm+1，n)=τ，λ=且ordλ(p)=s，当

时，存在参数为[n，n-1-2m-s，4]的距离最优p元循环码.

证明因为n|(p2m-1)且n＞pm+1，则ordn(p)=2m.设α∈是一个n次本原单位根，m(x)是α在Fp上的极小多项式，则deg(m(x))=2m.设(x)是在Fp上的极小多项式，下证deg((x))=s.显然，deg((x)) 是使(pm+1)(pl-1) ≡0(modn) 成立的最小正整数.注意到

于是deg((x))=s.设C是码长为n且生成多项式为g(x)=(x-1)m(x)(x) 的p元 循 环 码，则dim(C)=n-1-2m-s.

一方面，因为α0，α1，αpm，是g(x)的零点，由引理1，d(C) ≥4.另一方面，假设存在参数为[n，n-1-2m-s，≥5]的p元线性码.由球包界（1），

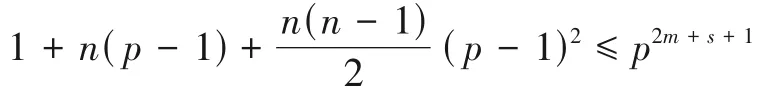
由此推出

矛盾.因此，C是最小距离为4的最优p元循环码.

由定理3推出，存在如下最优的p元循环码.

推论7设p是一个奇素数且m是一个正整数，则

（i）对任意的n|(p2-1)且n＞p+1，存在参数为[n，n-4，4]的距离最优p元循环码；

（ii）如果m≥2，对任意的e|(p-1)，s≥2 且s|m，存在参数为

的距离最优p元循环码；

（iii）对任意的ℓ|(p2-1)且ℓ ≥p+1，存在参数为[(p2+1)ℓ，(p2+1)ℓ-7，4]的距离最优p元循环码；

（iv）对任意的e|(p2-1)且e＜p2-1，存在参数为的距离最优p元循环码；

（v）如果p≥5 且m≥4，对任意的e|(p2-1)，存在参数为的距离最优p元循环码；

（vi）如果m≥3，存在参数为

的距离最优三元循环码；

（vii）如果m≥5，存在参数为

的距离最优三元循环码；

（viii）如果p≥5，对任意的ℓ|(p-1)且ℓ ≥2，存在参数为[(pm+1)ℓ，(pm+1)ℓ-2-2m，4]的距离最优p元循环码.

证明（i）～（viii）的证明类似，下面仅给出（v）的证明，其余略去.

由定理3，存在参数为[n，n-1-3m，4]的距离最优p元循环码.

下面构造最小距离是4的最优p元重根循环码.

定理4设p是一个奇素数，m和ℓ 是正整数，ℓ|(p2m-1)且ℓ ＞pm+1.设gcd(pm+1，ℓ)=τ，λ=且ordλ(p)=s，当

时，存在参数为[pℓ，pℓ-2m-s-3，4]的距离最优p元重根循环码.

证明与定理3类似，可证ordℓ(p)=2m.设α∈是一个ℓ 次本原单位根，m(x)是α在Fp上的极小多项式，且(x) 是在Fp上的极小多项式，则deg(m(x))=2m且deg((x))=s.设C是码长为pℓ且生成多项式为(x-1)3m(x)(x)的p元循环码，则dim(C)=n-3-2m-s.与定理3 类似可证，C是参数为[pℓ，pℓ-2m-s-3，4]的距离最优p元线性码.

由定理4推出，存在如下最优的p元重根循环码.

推论8设p是一个奇素数且m是一个正整数，则

（i）对任意的ℓ|(p2-1)且ℓ ≥(p+1)，存在参数为[pℓ，pℓ-6，4]的距离最优p元重根循环码；

（ii）如果m≥2，对任意的e|(p-1)，s≥2 且s|m，存在参数为

的距离最优p元重根循环码；

（iii）对任意的ℓ|(p2-1)且ℓ ≥p+1，存在参数为[(p3+p)ℓ，(p3+p)ℓ-9，4]的距离最优p元重根循环码；

的距离最优三元重根循环码；

（viii）如果p≥5，对任意的ℓ|(p-1)且ℓ ≥2，存在参数为[(pm+1+p)ℓ，(pm+1+p)ℓ-4-2m，4]的距离最优p元重根循环码.

注2定理3 和定理4 构造了两大类最小距离是4的最优p元循环码，其中定理4 构造了距离最优的重根循环码，从而说明重根循环码可以产生小距离的最优码.通过计算机搜索，本文构造了9 个码长不超243 的距离最优三元码，其中3 个码是维数最优码，详见表4，其中带*的码表示维数最优码.与码表［17］比较，本文构造了最优循环码.

表4 最小距离是4的最优三元循环码

注3当定理3 和定理4 的最优约束条件不满足时，仍可以构造达到码表［17］的最优码，下面举例说明.

例3设α是F3上不可约多项式x6+2x5+2x+2的根，则α是一个56 次本原单位根.设η=α28，则η在F3上的不可约多项式为x+1.设C1是码长为56 且生成多项式为(x-1)(x+1)(x6+2x5+2x+2)的三元循环码，由定理3的证明可得，C1是一个参数为[56，48，≥4]的三元循环码.由Magma 计算得，d(C1)=4.与码表［17］比较，C1是目前已知的最优三元线性码.设C2是码长为168 且生成多项式为(x-1)3(x+1)(x6+2x5+2x+2)的三元重根循环码，由定理4 的证明可得，C2是一个参数为[168，154，4]的三元重根循环码.与码表［17］比较，C2是目前已知的最优三元线性码.

4 结论

本文主要研究了重根循环码的纠错性能，并基于重根循环码构造了一系列最优的线性码.主要结果如下：（1）构造了几类最小距离是4 的最优二元重根循环码，特别地，构造了一类维数和距离都是最优的二元重根循环码，这一结果可以视作文献［7］中例3 的推广；（2）构造了一类最小距离是3的距离和维数都是最优的非二元重根循环码；（3）构造了两大类最小距离是4 的距离最优的非二元循环码.这些研究结果表明：重根循环码中存在小距离的最优线性码.自然地，是否存在最小距离大于4 的最优重根循环码是一个值得进一步研究的问题.文献［13］和文献［14］基于重根循环码的代数结构和最小Hamming 距离，确定了几类循环码的对距离，构造了几类极大距离可分符号对码，从而说明重根循环码有较好的纠正错误的能力.下一步将研究本文构造的最优码的对距离，从而构造参数优的符号对码.