适当扩充教材内容 满足不同发展需要

【摘 要】对教材内容进行适当扩充，可以在一定程度上满足不同水平学生的学习需要。《百分数的认识》的教学内容可以从百分数从何而来、如何展开以及去往何处这三个方面来进行扩充，这将有助于学生扩展认知结构，形成多角度看问题的意识，发展综合素养。

【关键词】小学数学;扩充内容;适合发展;《百分数的认识》

【中图分类号】G623.5  【文献标志码】A  【文章编号】1005-6009（2022）01-0064-05

【作者简介】王九红，南京市天正小学（南京，210037）党支部书记、校长，正高级教师，江苏省数学特级教师，江苏省“333高层次人才培养工程”第二层次培养对象。

【背景】

《义务教育數学课程标准（2011年版）》要求：人人获得良好的数学教育，不同的人在数学上得到不同的发展。从课堂教学层面来看，要落实这一理念，教师需要在教学目标、教学内容、教学方法等方面综合考虑，统筹实施。学生的学业水平和认知能力各具特点，这使得班级学情具有复杂性，而教科书是依据课程标准兼顾全国普遍学情编写的，因而需要教师根据实际情况进行具体处理。

综合考虑本班学情和百分数的知识特点等各方面因素之后，笔者将苏教版六上《百分数的认识》一课的教学目标设定为：引导学生通过自主探究，理解百分数的产生、意义及其与分数的关系，发展逻辑思维能力。因为学生已经学习过分数，有一些与百分数相关的生活经验，所以本节课适当扩充教材内容，适度提高教学目标要求。

【教学过程及分析】

一、引入

板书课题。

师：大家对百分数了解吗？我们今天来深入学习它。提出一个问题有时比解决一个问题更重要。大家来说一说，关于百分数，你想学什么？

生：什么是百分数？百分数怎么来计算？为什么要学百分数？百分数有什么用？百分数与别的数之间怎么转化？……

二、探究

（一）探究百分数从何而来

1.分析“谁的表现好”。

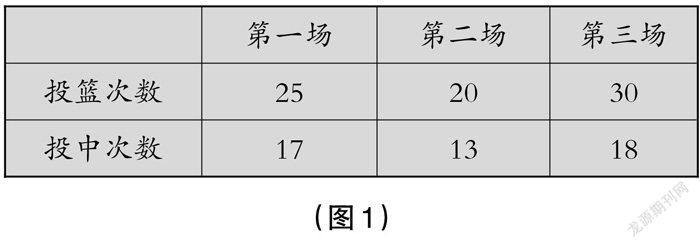
师（出示下页图1）：学校篮球队参加了三场比赛，王老师记录了其在这三场比赛中的投篮情况。根据投篮情况，你觉得球队在哪一场比赛中的表现好一些？理由是什么？

生1：我觉得第二场表现好些，第二场投中的次数虽然少，但投中的精准率高一些。

师：精准率是什么意思？

生1：比如说投了5个，5个都进了，精准率最高，一个都没中精准率最低。

师：有道理！但是三场都没有全中啊，你怎么知道第二场精准率高呢？

生1：我把它化成分数来算的，第一场投中的次数占投篮次数的[1725]，第二场[1320]，第三场[1830]。[1320]比其他两个分数都大，所以第二场精准率最高。

师（板书[1725]、[1320]、[1830]）：[1320]最大，第二场精准率最高，你们同意吗？

生2：我觉得第一场的精准率比第二场高一些。[1725]和[1320]换算成同一个单位，就是[68100]和[65100]。

师：大家有没有别的想法？（停顿一会儿）我觉得第三场表现好一些，这有没有道理？

生3：打球投球准很重要，但投中的次数也很重要。第三场投中的次数比其他两场都多，所以我觉得第三场表现也很好。

师：有道理！你们怎么看？比赛是以什么为标准来判定胜负的？

生：得分多。

师：对啊，谁得分多谁就赢，第三场进了18个球，是最多的，你能说不好吗？还有没有不同的想法？

生无人回答。

师：我现在又觉得第二场表现好了，这有没有道理？

生：有！因为第一场投25次，但只进了17次，投丢了8次。第三场投30次只中了18次，投丢了12次。第二场只投丢了7次。

师：你说第二场好，我说第三场好，他说第一场好，大家怎么看待这事儿？是的，三场比赛各有各的好，第一场精准率最高，第二场投丢的最少，第三场投进的最多。

苏霍姆林斯基说，不要让任何一个儿童在低于他才能的水平上学习。我们践行的原则，是每一个学生在学习中都应达到他力所能及的成就。为此，本节课对教材例题进行了两处改造：一是将“可以怎样比较这三场比赛的投篮情况？”改为“根据投篮情况，你觉得球队在哪一场比赛中的表现好一些？理由是什么？”，这一改变增强了问题的复杂性，拓展了学生的思维空间，有助于促进学生辩证思维的发展;二是将例题中的16改为17，这一“小动作”将教科书“陌生化”了，给课堂制造出了一个小惊喜——事先预习过的生1出错，引发了不同的意见。

2.探究百分数从何而来。

课件出示：从投中次数占比投篮次数的情况来看，学校篮球队在哪一场比赛中的投球水平更高一些？

师：对于投球来说，什么最重要？

生1：看谁投中的多，因为比赛看得分高低。

生2：得分多固然很重要，但如果你投的次数比别人多得多，并不能说明你投篮水平高。

师：你是说不能只看投中的次数，还要看投了多少个，对吧？

生3：我觉得应该看精准率。

师：精准率在篮球比赛中的术语叫得分率。看得分率，理由是什么？

生：因为你得分率高意味着你投中的多。

师：得分率高投中的就多，在什么情况下？

生：投的次数一样多的时候。

师：投的次数一样多，得分率越高，投中的次数就越多。现在，从得分率来看，哪一场的表现更好一些？

生：应该是第一场。因为三场比赛的得分率分别是[17/25]、[13/20]、[18/30]，把它们化成以100为分母的分数后分别是[68/100]、[65/100]、[60/100]，[68/100]最大，所以第一场的表现最好。

师：为什么要把它们的分母都变成100呢？

生：为了方便比较大小，100是25、20和10的最小公分母。

师：如果不这样，还有没有别的方法来比较它们的大小呢？

生：不用100也可以，只要保证它们的分母是公倍数就行。

师：分母是公倍数就行，200行不行？（行）300行不行？（行）只要分母是它们的公倍数就可以。在它们的所有公倍数中，100最小，最简便。我们如果不用这种方法，还有没有别的方法来比较？

生：可以把每个分数值都算出来，就是用分子除以分母化成小数，比较小数。

师：对，还可以化成小数来比较。大家算一下，能口算吗？

生：分子、分母都乘以4，就是[68/100]，就是0.68.

师：哈，你还是先变成分母是100的分数再化成小数。竖式计算比较麻烦，这样方便。其实，小数就是一个分母为100的分数。17÷25=0.68，0.68的小数单位是什么？0.01或[1/100]，它的分母是不是100？

要讓学生成为知识的主人，最好的办法就是让他们基于自己的需要进行建构。在分析“在哪一场比赛中的表现好一些”之后，教学活动聚焦“在哪一场比赛中的投球水平更高一些”这一问题，引导学生认识到以投中数占投球总数的分数值作为评判标准是最好的方式，且将分数的分母统一成100更便于比较。此时，学生不仅初步建构出了百分数的概念，还认识到百分数的分母是100只是一种选择，其他公倍数也可以做分母。占比结果也可以用小数表示，它与百分数表示的实质是一致的。

（二）学习百分数是什么

1.百分数的读写。

师：百分数有专门的表示符号。（板书：“%”）我们可以用这个百分号来表示这些数。（68%、65%、60%，大家一起读）大家发现百分数的读法与分数的读法有什么区别了吗？（百分数的读法中省略了“一”，更简洁）

2.百分号的来历。

师：一个符号的产生是有历史渊源的。百分号是怎么来的呢？

课件出示图2。

师：在美元里，分叫什么？（cent）“分”和“百”是怎么联系上的？不管是美元还是人民币，1元都是多少分？（100分）百分号就是这样演变来的。

3.百分数的意义。

师：百分号专门用于表示百分数，那什么是百分数呢？请大家一并回答这几个问题——（1）什么是百分数？（2）百分数与分数有什么关系？请画图表示。（3）百分数为什么要用“%”来表示？（4）已经有了分数，为什么还要学百分数？

生1：百分数就是分母是100的分数。

生2：我觉得百分数的概念并不是百分之几，而是一个数占另一个数的百分之几。

师：“占”是什么意思？

生：就是两个数相比较。

师：是的，所以百分数又叫百分比、百分率，它表示两个数之间的关系。分母是100的分数不是用来表示关系的，有这样的情况吗？

生：有，比如说[3/100]吨，它就是0.03吨，不是百分数。

师：分母为100的分数不一定是百分数，百分数的分母一定是100。想一想，什么是百分数？

生：表示一个数是另一个数的百分之几的数，叫作百分数。百分数又叫百分比或百分率。

师：哈，你说的和课本上一模一样。（出示课本上的定义）“是”就是刚才同学说的“占”，它表明两个数之间的关系不是增加或减少的关系，也不是倍数关系。老师是用什么表示“占”的？（出示图3）

生：分数线。

4.百分数与分数的关系。

师：百分数与分数之间有什么关系？能画图来表示吗？

生1展示图4。

师：这幅图，你能用一个词来表示它们的关系吗？

生1：包括，分数包括百分数。

师：“包括”，嗯，非常好！

生2：我觉得应该是“属于”。

师：谁属于谁？

生2：百分数属于分数。

师：数学上有一个词叫包含，分数包含百分数，百分数包含于分数。老师画了这样一幅图。（出示图5）图中增加了什么内容？

生：增加了一条竖线。分成两部分，一边表示数量，一边表示关系，而且把百分数分在了表示关系的那一边。

师：这条竖线将分数分成了两个不交叉的部分，要么表示数量，要么表示关系。余下的两个问题怎么回答？

生：我觉得用百分号来表示是为了跟普通的分数区分开。不这样写，它就有可能表示数量。要表示关系的话，用分数没有用百分数好。

师：表示关系的话，用分数没有用百分数好，是这样吗？大家请看。（出示图6）你有什么感觉？

生：用分数表示的那一栏看起来很乱，很难比较;用百分数表示的那一栏很清楚，一目了然。

师：所以，我们通常用百分数来表示占比的统计。

“什么是百分数”是本节课的核心内容，教材只编有百分数的意义、百分号和百分数的读写。此处的扩充，一是图文并茂、直观形象地呈现了百分号的演变过程，凸显了百分号的价值和百分数的优点;二是引导学生认识到分数既可以表示数量又可以表示关系;三是直观地呈现了百分数与分数的关系，不仅深化了学生对百分数意义的理解，还使学生学到的知识结构化更强。

三、强化

（一）基本练习

1.根据统计，某地学生的近视情况如图7所示，请你选一个百分数说说它表示的意义，并说说你有什么发现，对此有什么想法。

2.在生活中，你还见过哪些百分数？说说下面这段文字中的百分数的含义：我国新产业、新业态、新商业模式的“三新经济”快速发展。2012年到2019年，“三新”经济增加值占GDP的比重由14.8%提高到16.3%。

（二）知识拓展

1.认识十分数（折数、成数）、千分数（‰）、十万分数。

2.以“百分数”为主题写一篇数学小短文，不少于300字;文体不限，说明文、记叙文、议论文、诗歌都可以。

练习强化阶段的内容扩充主要立足于百分数去往何处，即选择百分数在实际生活中的应用。其目的是深化学生对知识的理解，培养学生的综合素养。具体做法分为三个层次。一是通过中小学生近视条形统计图和“三新经济”数据来加深学生对百分数的理解。二是让学生认识到百分数是一种表示占比的统计量，除了它，还有十分数（折数、成数）、千分数（‰）、十万分数等。百分数之所以使用最为普遍，是因为它的精确度比较适中。十分数比较笼统，千分数和万分数等则适用于占比份额较小的情况。从统计量的角度将它们呈现出来，有助于学生理解知识本质、扩展认知范围。三是通过以“百分数”为主题的短文写作来巩固和发展学生对百分数的认识，思维和想象空间较大，既有助于学生的个性化学习与表达，又有助于学生将数学知识与其他知识有机地融合起来。

总之，本节课的内容扩充包含三个方面，即百分数“从何而来”“如何发展”和“去往何处”。“从何而来”解决的是学习百分数的需要问题，这是让学生知道知识的来龙，其教学通常安排在课的开始阶段。“如何发展”解决的是百分数是什么、它与哪些知识相关联、它们之间有什么样的逻辑关系等问题，其教学通常安排在课的探究环节。“去往何处”解决的是百分数有什么用的问题，是让学生明白知识的去脉，其教学通常安排在课的强化阶段。

进一步看，为学生提供丰富多样的学习内容能满足不同水平学生的学习需要。正如苏霍姆林斯基所言，要防止差生落后的现象，就必须让天赋高、有才能的学生在他们力所能及的那些学科上和创造性活动领域里超越大纲的界限。当然，教师要依据学生的需要，为他们提供丰富多样的学习内容，而不能简单地增加数量和难度，否则就会导致学生学不了、不想学的问题产生。另外，教师也不能颠倒过来，以完成更多的内容为目的而采取硬性灌输的教学方式，使课堂沦落为刷题场、训练营。

3137500589221