一种新的基于正弦自适应权重的模拟退火粒子群优化算法
2022-03-16甘地
甘 地
(中南大学机电工程学院,湖南 长沙 410000)
粒子群算法[1]是模拟群体智能所建立起来的一种算法,最早在1995 年由美国的Eberhart 和Kennedy 两人提出。由于它运行逻辑简单、需要调试的参数少、容易实现,因此受到大量学者的研究与应用。如今,在NP 问题求解、图像处理[2]、人工神经网络建模[3]和车辆路径优化[4]等领域时常可以见到对粒子群算法的使用。然而粒子群优化算法也存有一些缺点,如,易陷入局部最优解,运行末期收敛速度减缓、收敛精度低等。为改善这些缺陷,学者们进行了大量的研究。文献[5]将研究重心放置在粒子群算法的惯性权重上,提出一种按正弦变化惯性权重的粒子群优化算法。文献[6]提出对惯性权重的自适应变化方案,即自适应权重的粒子群算法。文献[7]在研究了细菌觅食算法(BFO)的特点后,将BFO 算法中的趋化和迁徙算子引入粒子群算法,提出了PSO-BFO 混合算法。文献[8]将模拟退火的思想融入粒子群算法中,提出了基于模拟退火的粒子群算法。上述文献通过改善权重系数,或将粒子群算法与其他算法相结合,或多或少地对算法性能进行了加强。
本文在分析了粒子群算法的优缺点,以及模拟退火算法的运算原理后,将模拟退火的思想引入粒子群算法中,提出基于模拟退火的粒子群算法。基于惯性权重对算法运行效果的重要作用,提出一种正弦自适应变化的惯性权重。该算法结合了粒子群优化算法的全局搜索能力模拟退火算法的一定概率跳出局部最优解的优点以及正弦自适应变化的惯性权重,改善了粒子群算法易陷入局部最优解的问题,增强了运算末期的收敛速度和收敛精度。
1 标准粒子群算法
Eberhart 博士和Kennedy 博士基于对鸟群觅食行为的学习和模拟,创建了粒子群优化算法。该算法的核心思想是在问题求解空间中,通过个体间信息互相流通,使得群体的运动逐渐从无序演化为有序,从而求解出最优值。在运算前,粒子群算法会初始化若干个粒子,每个粒子都代表目标函数的一个解,具有位置向量和速度向量。将粒子的位置向量带入目标函数,求得的值被称为粒子的适应度值。在每次迭代中,群体中粒子位置的更新会受到自身历史最优解和群体当前最优解的影响,有朝向这两个最优解移动的趋势,从而确定粒子在下一次迭代时的位置和速度如何改变,并更新自身历史最优解以及群体当前最优解。最终通过不断地迭代,寻得目标函数的最优值。
假设在一个D 维空间中有N 个粒子,粒子i 在t 时刻的位置为xi(t)=[xi1(t),xi2(t),...xiD(t)],飞行速度为vi(t)=[vi1(t),vi2(t),...viD(t)]。将粒子i 的位置xi带入目标函数得到适应度值,对比该粒子历史最佳适应度值,得到该粒子从迭代运算以来的历史最优解,记为pi=(pi1,pi2,…piD)。比较空间中所有粒子的个体最优解,取最小的那个粒子的位置作为整个粒子群迄今为止的群体最优解,记为pg=(pg1,pg2,...pgD)。粒子群算法对粒子速度和位置的更新采用以下公式:
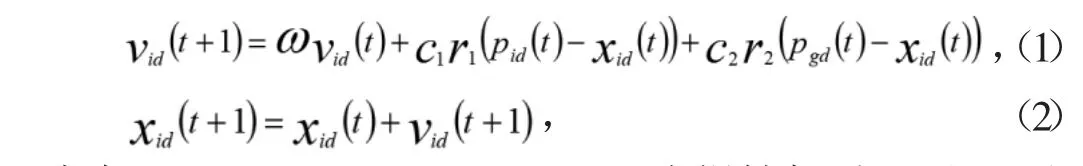
式中:i=1,2,3...N;d=1,2,3...D;ω 为惯性权重因子;C1和C2为学习因子,也称加速因子,一般取负数;r1和r2为两个介于[0,1]的随机数;
上式中,公式1 为速度更新公式,公式2 为位置更新公式。其中速度更新公式分为3 个部分,第1 部分是惯性部分,粒子受惯性影响,会向着粒子上一时刻的速度方向移动;第2 部分是自我认知部分,由于受到自身历史最优位置的影响,粒子有回到该位置的倾向;第3 部分是社会认知部分,粒子处在种群中,受到当前最优粒子的吸引,有去到当前最优粒子位置的趋势。种群中的粒子通过公式1 和2 进行更新,经过多次迭代,逐渐向全局最优解靠近,最终在粒子空间中搜索到函数最优解。
2 模拟退火算法
1953 年,N.Metropolis 等人提出模拟退火算法,随后S.Kirkpatrick 等人在1983 年首次将其引入组合优化问题的求解之中。由于一般组合优化问题类似于物理中固体的退火过程,从而以此为出发点引出该算法。算法起初给定一个较高的温度T0,随机生成一个初始解,然后采用Monte-Carlo 迭代求解策略不断产生新解,利用Metropolis 准则有一定概率接收较差的解的方法,判断是否用产生的新解代替上一代的旧解,并在迭代过程中不断降低退火温度,最终得到问题的最优解。Metropolis 准则定义了在某个温度T 下物体从状态i 转移到状态j 的能量概率:
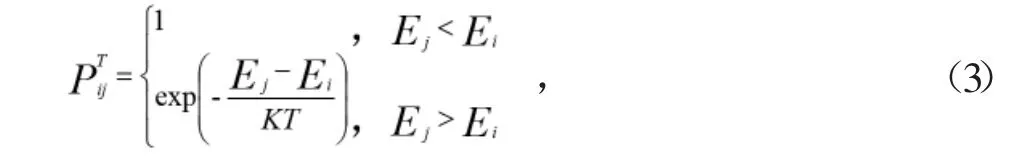
式中:Ei和Ej分别为固体在状态i 和j 下的内能;K 为玻尔兹曼常数。
全局搜索算法一般都会有陷入局部最优解的问题的存在,而模拟退火算法采用Metropolis 准则,使得算法在搜索运行过程中有接收较差解可能性,从而有利于算法跳出局部最优解,克服该问题。然而,模拟退火算法收敛速度慢、参数调整困难等缺点,使其应用并不普遍。
3 基于模拟退火的粒子群算法
3.1 正弦自适应权重
惯性权重是粒子群算法中需要调节的重要参数。惯性权重值越大,粒子在更新过程中的搜索步长越大,全局搜索能力越强;反之,粒子的局部搜索能力越强。因此为提高粒子的搜索能力,使用正弦自适应权重的策略如下:
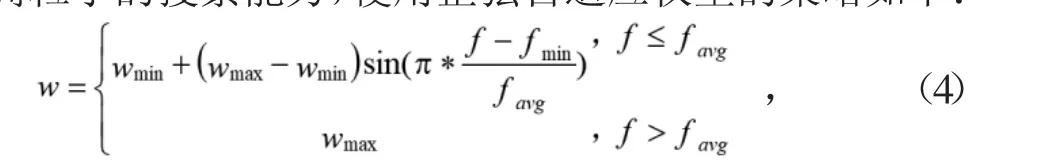
式中,wmax和wmin为惯性权重的最大值与最小值;f 为粒子的当前适应度值;favg为当前全部粒子的平均适应度值;fmin为当前全部粒子适应度值的最小值。
正弦变化的惯性权重[5]让算法在运算初期能够有较小的权重值,粒子具有较强的局部搜索能力,使得粒子获得个体最优解。在算法运行的中期,随着正弦函数的变化特性,权重值慢慢变大,粒子开始进行全局最优解的搜索。而在算法运行的后期,惯性权重又慢慢变小,粒子进行细致的局部搜索,寻找该区域的最优解,及全局最优解。自适应变化是指在每一次迭代过程中,以每个粒子的适应度值和所有粒子的平均适应度值的大小做判断,决定该粒子的权重该如何变化的方式。引入正弦自适应权重策略,有利于粒子在局部和全局空间中动态的搜索。
3.2 算法流程
由于粒子群算法存在易陷入局部最优解的问题,而模拟退火算法具有一定概率接收较差解的特性,因此将其与粒子群算法进行融合,提出基于正弦自适应权重的模拟退火粒子群算法,该算法融合方式有利于改善粒子群算法的全局搜索能力。采用正弦自适应权重策略,提高收敛速度和精度。该算法基本流程如下:
(1)设置种群大小N、粒子维度D,初始化粒子的速度和位置;
(2)计算每个粒子的适应度值fitness(xt),并将每个粒子的个体最优解存储在pi中,所有粒子中的全局最优解存储在pg中;
(3)设置初始温度T0=pg/ln5;
(4)根据式(4)对惯性权重进行更新;
(5)依据公式1 和2 对粒子进行更新,并计算适应度值fitness(xt+1);
(6)采用模拟退火算法的Metropolis 机制,若fitness(xt+1)
(7)进行退温操作Tt+1=0.9*Tt;
(8)判断是否满足终止条件,如果满足则输出pg;否则,转到第4 步。
4 仿真实验
为验证上述基于正弦自适应权重的模拟退火粒子群算法(SASAPSO)的性能,采用文献[1]的4 个基准函数对其进行测试,并与标准粒子群算法(PSO)、一种改进的粒子群算法[9](SAPSO)和基于自适应权重的粒子群算法[6](AWPSO)进行仿真实验比较。分别利用这4 种算法对每个基准函数进行50 次最优值求解,通过实验仿真得到4 种算法下各个基准函数的平均适应度值与迭代次数的关系。
4 个基准函数如下。

其仿真结果如图1、图2、图3、图4 所示。
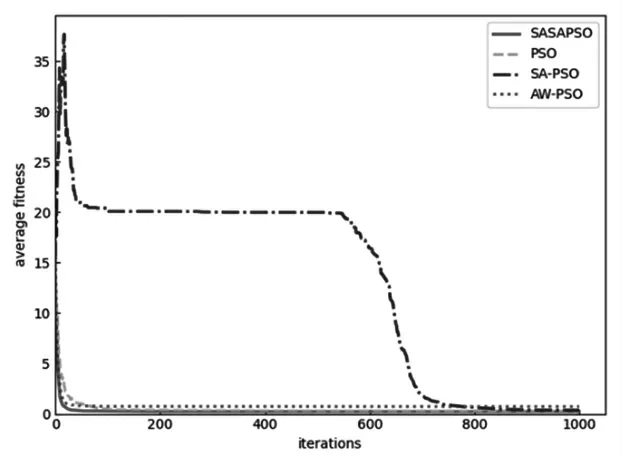
图1 Griewank 函数的迭代曲线
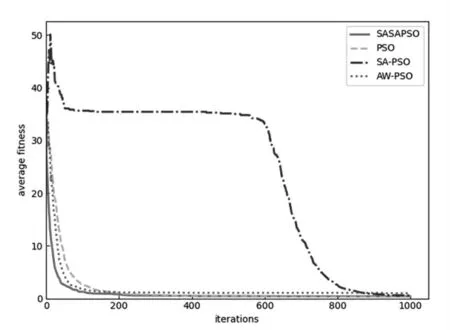
图2 Rastringin 函数的迭代曲线
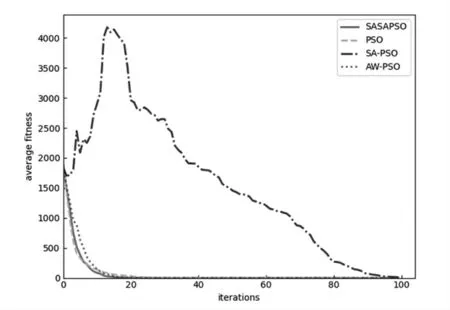
图3 Sphere 函数的迭代曲线
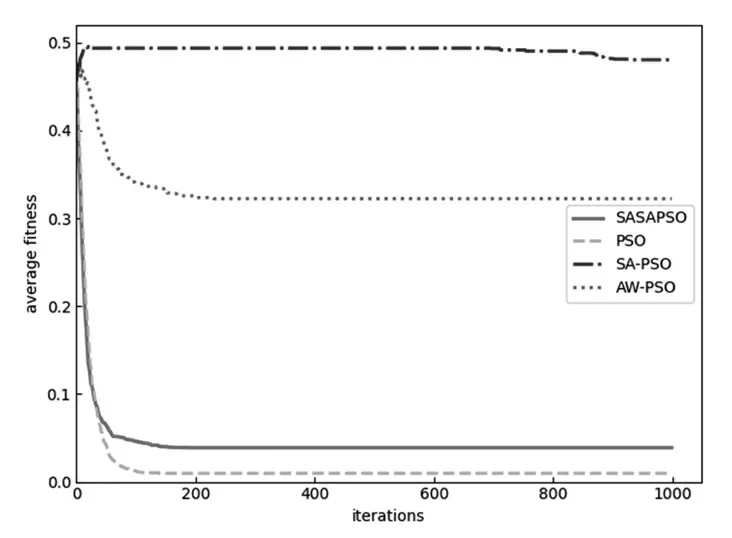
图4 Schaffer 函数的迭代曲线
由图示可以看出,在Griewank 函数的迭代曲线中,SASAPSO 算法收敛到最优值的迭代次数为20 次,收敛的迭代次数略大于AW-PSO 算法,但SASAPSO 算法的收敛精度是4 个算法中最高的;在Rastringin 函数的迭代曲线中,SASAPSO 算法收敛到最优值的迭代次数为100次,是4 个算法中最少的,并且收敛精度最高;在Sphere函数的迭代曲线中,4 个算法的收敛精度相当,但SASAPSO 算法收敛到最优值的迭代次数为18 次,是4 个算法中最少的;在Schaffer 函数的迭代曲线中,AW-PSO 算法和SASAPSO 算法收敛到最优值的迭代次数同为200次,但SASAPSO 算法的收敛精度明显高于AW-PSO 算法。因此,综合4 个算法在4 个测试函数下的仿真结果,SASAPSO 算法的收敛速度和收敛精度是4 个算法中最高的。
5 结论
本文提出的基于模拟退火的粒子群算法(SASAPSO),以粒子群算法为主体框架,为改善粒子群算法易陷入局部最优解的问题,引入模拟退火机制,增强了粒子群算法的全局搜索能力。采用正弦自适应惯性权重的策略,有效地提高了算法的收敛速度和收敛精度。在4 种基准函数的仿真测试下,与他人提出的3 种算法进行对比。仿真结果表明,SASAPSO 算法的收敛速度和收敛精度更高。
