基于矩阵光学的多程激光放大器准直系统模型分析
2022-03-16高光波孟繁禹
唐 玮,高光波,孟繁禹
(中国航空制造技术研究院,北京 100024)
当前多程放大技术成为高功率固体激光装置的主要发展方向,随着多程放大技术的实现,高功率固体激光装置的光路结构更复杂、光学元器件更多。如果采用人工调整光路,存在工作量较大,速度较慢、重复性较差、且精度低等问题。为了对激光光路进行调试和维护,建立光路准直的数学模型和调整方案很有必要[1-2]。
矩阵光学采用矩阵代数方法研究光学问题,具有处理问题简单和便于计算机求解的优点,易于获得解析解。用矩阵光学方法,建立了多程放大自动准直系统的远、近场光斑偏移量与调整量的解析表达式;验证了该自动准直系统光路原理及调整方法的可行性。以某型放大器为例进行分析,四程增益设计指标>200倍,考虑到机械结构件因振动和小温度变化产生的光束角漂移量,该放大系统的准直调整关联性大,调整难度高[3-5]。
1 多程放大系统的光学原理
本研究所述的多程放大系统,均以四程放大为例,通过多程偏振态的控制,实现了放大介质的多次重复利用。其光学原理设计如图1所示。其光路传递过程如下。

图1 光学原理图Fig.1 Optical schematic diagram
(1)输入的种子光为竖直偏振,经过反射镜M1和偏振分光棱镜PBS1,经过磁光隔离器FR1和旋转半波片HP,其偏振方向由竖直偏振方向改变为水平偏振方向,通过偏振分光棱镜PBS2后注入到前级空间滤波器1中,依次经过前级增益介质和前级空间滤波器2后,实现第1程放大。
(2)第1程放大光经过磁光隔离器FR2和反射镜M2后再次经过磁光隔离器FR2,其偏振方向由水平偏振转变为竖直偏振方向,光路依次经过前级空间滤波器2、前级增益介质、前级空间滤波器1、实现第2程放大。
(3)第2程放大激光通过偏振分光棱镜PBS2和反射镜M3、M4后返回,再次通过偏振分光棱镜PBS2、前级空间滤波器1、前级增益介质、前级空间滤波器2实现第3程放大,此时偏振方向仍为竖直方向。
(4)第3程放大激光经过磁光隔离器FR2和反射镜M2后,再次经过磁光隔离器FR2,其偏振方向由竖直偏振转变为水平偏振方向,依次经过前级空间滤波器2、前级增益介质、前级空间滤波器1,实现第4程放大。
由于系统振动、温度热漂移、结构件时效等因素影响,激光光路会存在一个随时间改变的漂移,因而该激光器必须具备能够对光路进行调整的准直系统[6-8],尤其是对焦斑相对于滤波小孔的位置进行调整。在前级光束满足准确注入的条件下,该激光准直系统需要通过调整M2、M4两片反射镜,实现激光远近场的准直要求。
综上所述,可以看出,该激光系统的准直调整关联性大,调整难度高。通过建立系统数学模型,探讨上述反射镜之间的关系,利用远、近场的反馈,准确、高效地实现准直调整[9-10],是多程放大系统的重要任务之一。
2 多程放大准直系统数学模型建立
通过研究多程放大系统的特点,应用矩阵光学原理,建立放大准直系统的数学模型。该模型采用笛卡尔坐标系,从左至右的z轴是系统的主光轴,同时也是光线的传播方向。在近轴光学的条件下,光学系统是绕z轴旋转对称的,因此对一条特定的光线而言,仅需考虑与z轴垂直的x轴方向的特性。光线方向定义为:沿z轴逆时针方向为正,顺时针方向为负。因此,该光线在z位置的光束信息可以用两个参数表示:该光线到z轴的距离x(z)和光线与主光轴的夹角θ(z)。近轴光学条件下

则该光线的参数可以表示为

进一步的,在柱坐标系条件下,i点光束的信息可以表示为

式中,ri表示光束上i点相对于光轴的位置;θi表示光束上i点相对于光轴的夹角[1]。
图2描述了单个滤波器4f系统的数学模型。透镜L1和R1实现共焦,其焦距分别为f1和f2,Φ1所在位置为滤波小孔。激光光束自系统的左侧进入近轴透镜L1,自右侧R1出射,经过平面反射镜M1反射后回到原光路。若M1失调,镜面与主轴的失调角为Δθ4,依照上文的分析,该系统的光学矩阵Ai可以写作
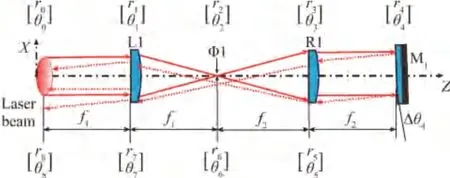
图2 单个滤波器数学模型Fig.2 Single filter mathematical model
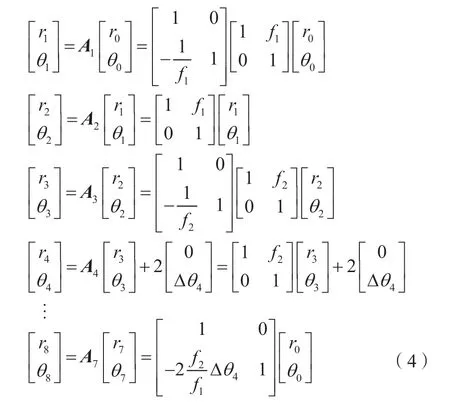
返回光矩阵(A5~A8)的形式与入射光相同,区别在于光学矩阵的前后顺序,此处不重复描述。为了使焦斑能够准确地通过滤波小孔,需要满足A8=A0,即
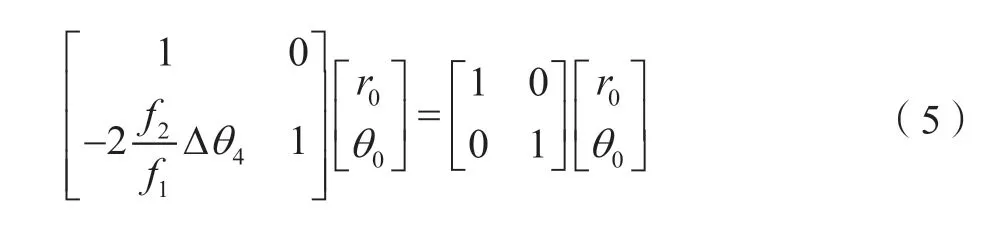
只需要顺时针调整M1镜,使得Δθ4=0,即可完成该滤波器的准直,这一数学模型的结论和实际光路的调整方式也是符合的。
利用前面的模型,对多程放大系统参数进行矩阵化处理,如图3所示。这里的光路计算均按近轴、透镜按照薄透镜、半波片按照薄透镜进行近似;磁光隔离器、偏振分光棱镜等按照折射率为n的光学平板处理。模型分析如下。
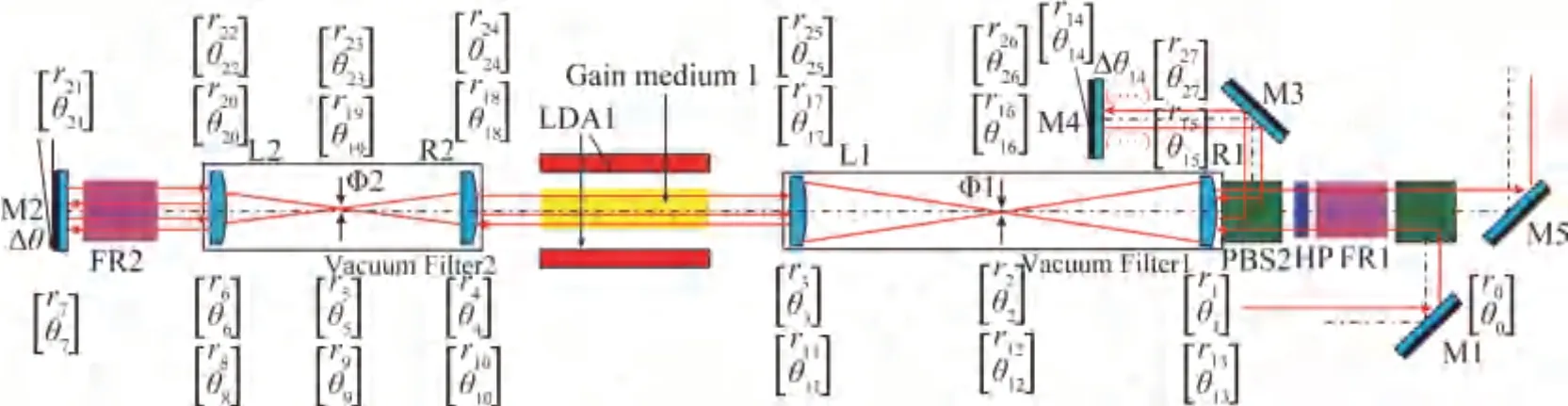
图3 多程放大准直系统模型Fig.3 Model of auto-alignment system for multi-pass amplifier system
系统入射点的光学矩阵为

经过M1、PBS1、FR1、HP、PBS2传输到R1处,此时光学矩阵为

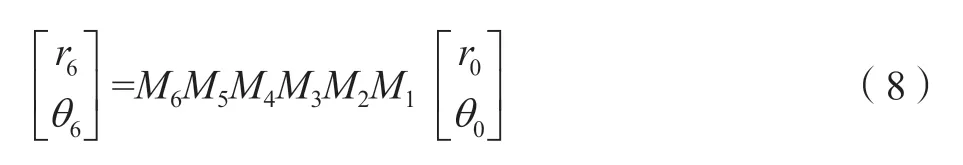
式中,
经过计算、化简后得到如下表达式
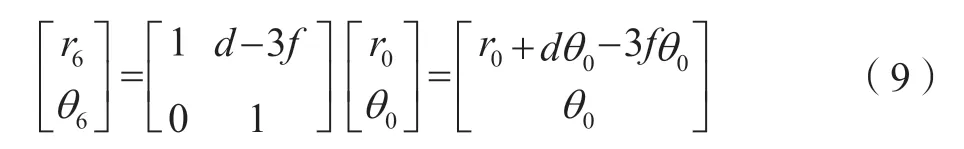
式中,d为透镜的位置;f为透镜的焦距。
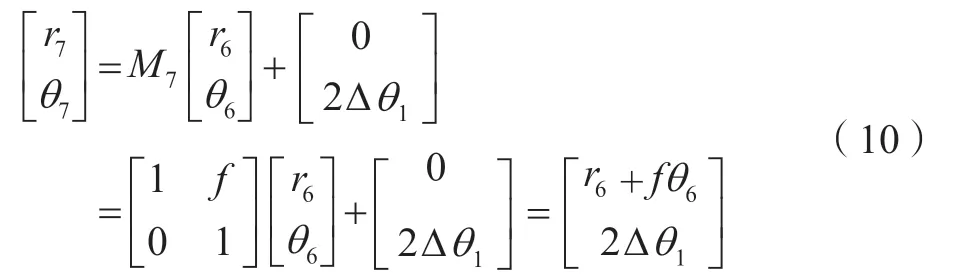

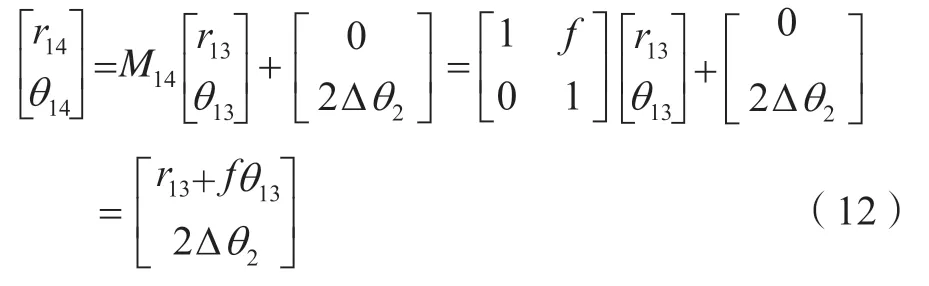
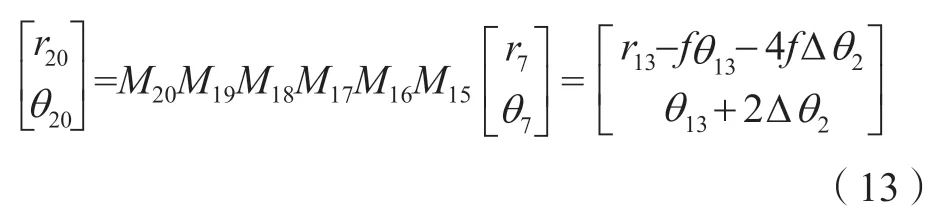
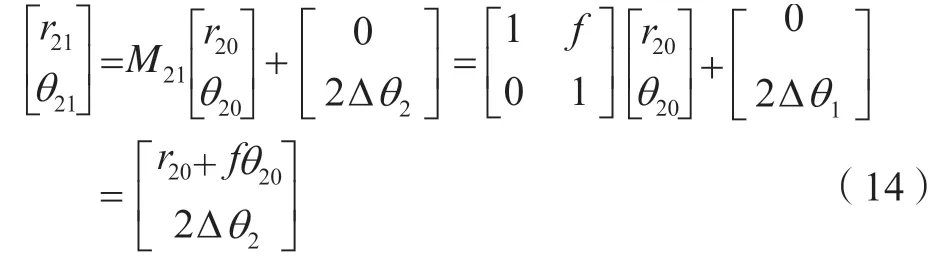

3 多程放大准直系统数学模型分析
由式(9)的计算结果可知,对于第一程光束而言,其输出为

影响因素为r0、θ0、d和f,当滤波器透镜的焦距f与输入位置d一定时,精确调节M1,第1程光束准确穿过前级空间滤波器1和前级空间滤波器2的光阑,第1程光束就具有唯一性;由式(11)的计算结果可知,对于第2程光束而言,其输出为

影响因素为r6、θ6、d和f,当滤波器透镜的焦距f与输入位置d一定时,精确调节M2与主光轴的失调角θ1,实现第2程光束准确穿过前级空间滤波器2和前级空间滤波器1的光阑。同理,调节M4与主轴的失调角θ2,实现第3程光束准确穿过前级空间滤波器2和前级空间滤波器1的光阑,第四程光束不需要调节就可以满足要求。
4 试验装置
多程放大器的作用主要是增益提取,根据设计指标,四程增益为200多倍,采用了单通四程放大器。试验装置如图4所示。

图4 多程放大器试验装置图Fig.4 Diagram of multi-pass amplifier test equipment
在实际的调节过程中,通过调整M1可满足第1程光束要求,然后再调整M2与主光轴的失调角θ1,使光束位置满足要求,满足第2程光束要求,调节M4与主轴的失调角θ2,第3程光束就具有唯一性;第4程光束不需要调节就可以满足要求。整个装调过程与理论分析的结果具有一致性。
多程放大器的四程光能量及光斑分布如表1所示,满足指标要求。
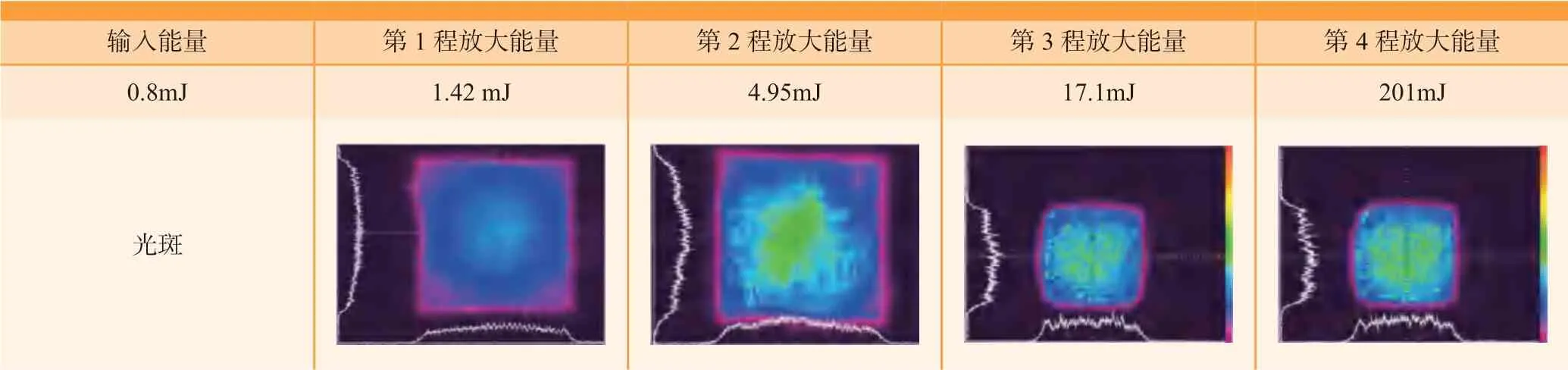
表1 多程放大器的四程光能量及光斑分布Table 1 Four-process amplifier energy and facula distribution of multi-pass amplifier
5 结论
本研究用矩阵光学方法,建立了多程放大自动准直系统数学模型;分析了实物装调的方式方法,验证了该自动准直系统光路原理可行性,该自动准直系统光路已在样机上得到验证,证明调试方法合理有效,满足了系统指标。
