水下非正交声学角反射器声散射特性研究

谢涛涛, 罗 祎, 肖大为

水下非正交声学角反射器声散射特性研究

谢涛涛, 罗 祎, 肖大为

(海军工程大学 兵器工程学院, 湖北 武汉, 430033)

水下角反射器具有较强的远场声散射特性, 由于存在生产装配误差, 标准正交金属角反射器无法满足各板面绝对垂直, 因此生产误差是对角反射器声散射特性产生影响的重要因素。文中研究非正交角反射器的声散射特性, 利用夹逼定理思想改变标准角反射器平板之间的夹角为90°、85°和80°, 并进行定性分析; 采用结构建模软件ANSYS依次对非正交二面角、三面角反射器进行模型构建及网格划分; 再利用声学仿真软件SYSNOISE根据结构有限元+流体边界元的方法对其远场声散射特性进行仿真, 并与标准正交角反射器在相同的载荷条件与声场条件下的声散射特性进行对比, 得到声波不同入射角度下的目标声散射强度以及目标强度随入射声波频率的变化规律。仿真结果表明, 正交角反射器声散射特性优于非正交角反射器, 正交二面角反射器优于三面角反射器, 二面角反射器生产误差在2°以内不会对声散射特性造成实质性影响。

水下角反射器; 生产误差; 结构有限元; 流体边界元; 声散射; 目标强度

0 引言

角反射器由金属板材或者覆盖金属的其他材料与非金属组成, 具有结构简单、回波能力强、造价低等优点, 最初用于雷达电磁波对抗领域[1-3]。水下角反射器作为一种无源声反射装置, 在声波入射其表面时, 不仅会产生镜面反射, 还会产生绕射、透射和远场散射, 因其较好的声散射特性, 可作为声学假目标对主动声呐进行诱骗[4-6]。

金属平板是构成角反射器的基础, 相互垂直的金属板构成的角反射器反声性能较好, 但水下角反射器在实际加工条件下并非相互垂直, 声波入射到角反射器时经过多次反射回到入射声源处, 而角反射器平板间角度的变化会直接影响到角反射器的声回溯特性, 使得声波反射方向无序化, 从而减小了声源处所能接收到的目标强度。由于生产工艺的限制, 满足各平板之间相互垂直的条件, 无疑会极大地增加水下角反射器的生产成本。因此, 研究水下非正交角反射器的声散射特性具有重要意义。

毕亚峰等[7]结合Biot流体理论进行了基于变换声学的角反射器分析; 张小凤等[8]结合“柱的方法”研究了水下充气圆柱的声散射特性; 魏克难等[9]通过耦合声学边界元法(boundary element method, BEM)分析了水中弹性球壳的声散射特性; Zeidan[10]采用解析法分析了有限长加肋柱状结构的声散射情况; 陈鑫等[11-12]通过流固耦合的方法对水下标准二面角反射器的声散射特性进行了研究, 结合声束弹跳法验证了SYSNOISE软件仿真数据的准确性, 并对产生的误差进行分析, 认为加工角度误差使得角反射器平面不垂直会对角反射器声散射特性造成较大影响。

文中以正交角反射器为基础, 通过结构有限元+流体边界元的方法, 分别对不正交弹性二面角和三面角的声散射特性进行研究, 分析角度误差对角反射器声散射特性的影响, 得出不影响角反射器声散射特性的加工误差范围。

1 有限元-边界元基本理论

1.1 有限元法简介

有限元法的基本概念是用较简单的问题代替复杂问题后再求解。它将求解域看成是由许多称为有限元的小的互连子域组成, 对每一单元假定1个合适的(较简单的)近似解, 然后推导求解这个域总的满足条件(如结构的平衡条件), 从而得到问题的解。

有限元法实际上就是求解下面的方程

另一方面如果能知道模态, 通过模态叠加, 就可以得到声腔的反应

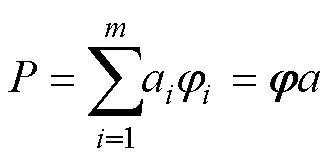
这样就转化为求解系数向量的问题, 通过求解下列方程得到特征值向量

1.2 BEM简介

BEM又称边界积分方程法, 是将待求解问题的微分方程变成边界上的积分方程, 再引入边界上的有限个单元将积分方程离散, 得到只含有边界上节点未知量的方程组, 并进行数值求解。由于BEM是将区域上的控制方程转化为沿着区域边界的积分方程, 因此只需要定义边界上的单元, 结合边界条件求解, 这样就使处理问题的维数降低一维, 可以有效地将复杂的三维几何模型简化为二维图形。与同样复杂的完整三维有限元模型相比, 该模型更小、更易于创建和检验, 并在更短的时间内得出结果。但BEM所建立方程组的系数矩阵稠密, 而且一般非对称, 矩阵元素分量的计算量很大, 增加了计算时间。由于BEM所利用的微分算子基本解能自动满足无限远处的条件, 因而BEM特别便于无限域以及半无限域问题。BEM又可分为直接BEM和间接BEM。

1) 直接BEM的系统方程为

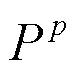
2) 间接BEM的系统方程为

1.3 有限元耦合间接边界元

在求解空气中结构的声散射问题时, 由于空气的特性阻抗较之于结构阻抗十分微小, 基本可以忽略空气对于结构振动的影响。但对于水中结构, 由于水的声特性阻抗是空气的100多倍, 且固体的结构阻抗和水的特性阻抗相差1个数量级, 会产生流体与结构之间的耦合振动, 因此不能忽略水的阻抗作用。因此水中结构的声散射问题实质上是对流体结构振动的复合问题, 需进行声振耦合计算, 使用结构有限元+流体边界元的方法对问题进行分析解决。

在物理坐标系中, 直接边界元流体模型和有限元结构模型的耦合系统方程如下

2 模型构建及分析流程

文中采用ANSYS和SYSNOISE软件相结合的方式对不标准水下声学角反射器的声散射特性进行了仿真分析。SYSNOISE善于处理复杂结构的振动声学问题, 但没有有限元及边界元模型网格生成的前处理功能。因此, 先采用ANSYS进行模型构建及网格划分, 而后将网格模型以*.cdb的格式输出。SYSNOISE则负责导入此网格文件, 继而进行结构-声耦合后处理, 具体流程见图1。

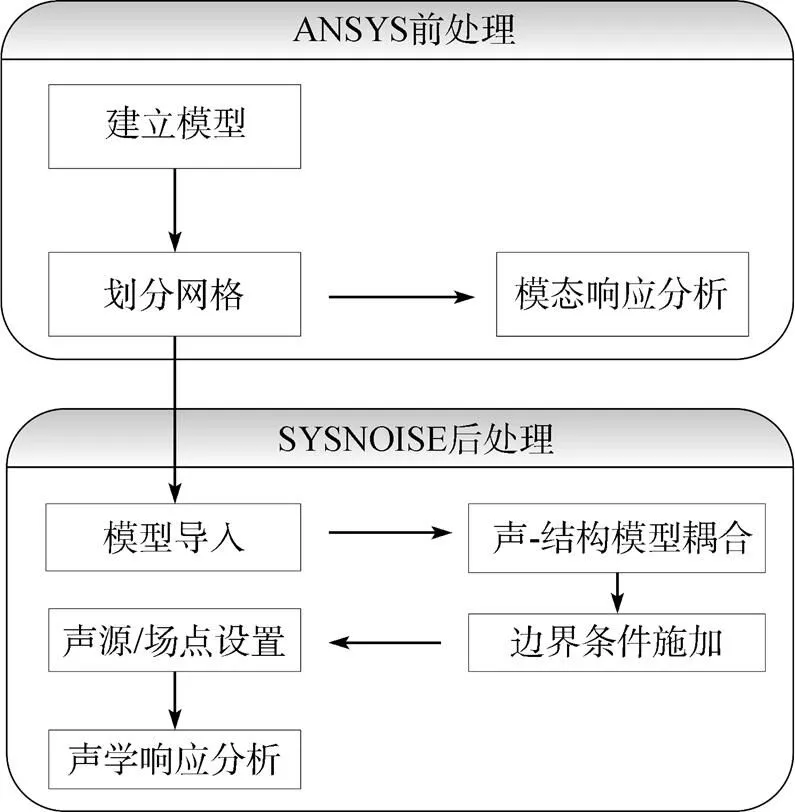
图1 仿真分析流程图

2.1 ANSYS模型前处理

在ANSYS模型前处理中, 为了减少计算误差, 在建模时需通过布尔运算实现对复杂结构的精确建模。水下角反射器属于薄壁结构, 采用SHELL181类型单元对模型进行网格划分, 为了保证计算精度, 网格大小划分小于入射声波波长的1/6, 网格法线方向一致。二面角反射器及三面角反射器结构网格模型如图2和图3所示。

图2 二面角反射器网格划分图

图3 三面角反射器网格划分图

弹性金属板的声散射特性与金属板厚度和入射波频率有关, 利用MATLAB软件对水下弹性板声反射系数进行研究, 考虑到金属密度及实验所用信号发生器最高可输出15 kHz声波, 因此分析0～20 kHz内0～20 mm厚弹性金属板的反射系数, 如图4和图5所示。

图4 弹性金属板反射系数随入射波角度及频率变化

图5 反射系数随金属板厚度变化曲线

由图可知, 弹性金属板反射系数随入射波频率增大而增大, 入射波频率在12 kHz时, 反射系数趋近于1。入射波频率为15 kHz时, 反射系数随金属板厚度增大而增大, 在板厚超过10 mm时, 反射器系数大于0.85, 在板厚为18 mm时, 反射系数趋近于1; 考虑到金属的密度及角反射器体积, 取角反射器厚度为10 mm。

完成模型构建与网格划分后, 将网格数据输出为*.cdb文件, 便于导入SYSNOISE软件中进行声学后处理分析。

2.2 SYSNOISE声学后处理

在SYSNOISE中进行声-结构耦合处理时, 需要先将结构模型的分析类型定义为FEM Structure, 导入模型网格后进行检查及材料属性定义; 流体边界元模型需定义为BEM Indirect, 同理在模型网格导入后仍需定义流体材料属性及耦合面, 最后完成有限元结构模型与流体边界元模型的耦合。

为了使计算满足远场条件, 定义声源距离声场中心100 m, 声源入射波为平面波, 入射声波幅值为1 Pa, 频率设定为0～15 kHz, 方向为声场中心方向。场点与声源的位置相同, 满足收发合置的条件。

定义求解频率范围和步长, 对模型网格和场点上的声学量, 如声压、声强和振速等参数进行计算。场点计算完成后重置声源, 再对场点进行一次运算, 此时得到的计算结果是散射声场的声学量, 不含入射声场。根据需要提取指定场点在某频率范围内的计算结果, 绘制该场点的频率响应函数曲线。

3 仿真算例分析

3.1 弹性非正交二面角声散射特性分析

标准二面角反射器是由2块矩形金属板相互垂直构成(如图6所示), 当声波入射时, 由于方向回溯特性, 可产生较为理想的后向反射。

图6 标准二面角反射器示意图

平板互不垂直时, 构成了非正交二面角反射器, 通过研究非正交角反射器的声散射特性, 分析加工误差对角反射器带来的影响。

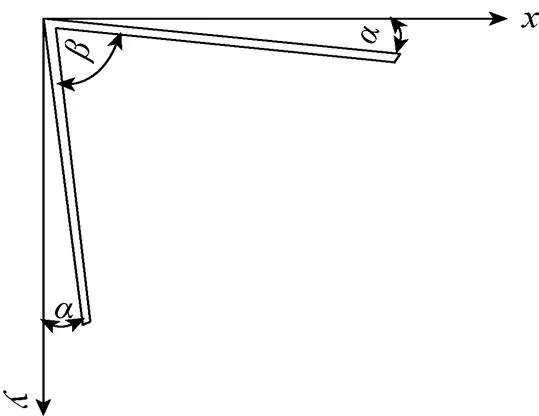
图7 非正交二面角反射器示意图

在入射声波属性一致的前提下, 分析图8～图10可以得出如下结论。

图8 不同入射频率下90°二面角反射器目标强度随入射角变化曲线

1) 二面角反射器对入射声波具有较强的频率特性, 目标强度随入射声波频率的增大而增大;

2) 二面角反射器目标强度随平板间误差角变化明显, 误差越大, 目标强度越低, 且波动性越强;

图9 不同入射频率下85°二面角反射器目标强度随入射角变化曲线

图10 不同入射频率下80°二面角反射器目标强度随入射角变化曲线

3)目标强度随声波入射角变化规律基本一致, 高频声波入射时, 始终在45°处取得最大目标强度。

基于二面角反射器对入射波的频率特性, 将15 kHz高频下二面角反射器目标强度进行提取对比, 如图11所示, 可知:

1) 正交角二面反射器目标强度在相同入射条件下大于非正交二面角反射器, 90°正交角反射器目标强度比85°二面角反射器大6 dB;

2) 正交角反射器散射宽度优于非正交角反射器, 在入射角为30°～60°范围内具有较强的目标强度值;

3) 90°二面角反射器随入射波角度改变目标强度变化较小, 稳定性强, 85°和80°非正交角反射器则波动性较大。

图11 不同夹角下15 kHz二面角反射器目标强度随入射角变化曲线

综上所述, 二面正交角反射器声散射特性优于非正交角反射器, 在相同入射条件下具有更强的目标强度与散射宽度。

3.2 弹性非正交三面角反射器散射特性分析

标准三面角反射器是由3块三角形板相互垂直构成的(如图12所示), 声波在入射后可在一定象限内形成较强的散射声场, 因此工程上常用多个三面角反射器组合来制作具有较大散射宽度的角反射器。

图12 标准三面正交角反射器

非正交三面角反射器(如图13所示), 是改变轴方向2个反射面Ⅰ、Ⅱ之间的夹角, 使其两面夹角依次也为90°、85°和80°。

图13 非正交三面角反射器

三面角反射器结构参数和分析参数与3.1节相同, 仿真结果如图14～图16所示。

图14 不同入射频率下90°三面角反射器目标强度随入射角变化曲线

图15 不同入射频率下85°三面角反射器目标强度随入射角变化曲线

图16 不同入射频率下80°三面角反射器目标强度随入射角变化曲线

在相同的入射条件及载荷条件下, 可知:

2) 非正交三面角反射器最大目标强度值无固定点, 频率曲线波动性较强, 而正交角反射器则在45°处取得最大值。

同理, 将三面角反射器高频入射波下频率与误差角数据进行提炼可以得到如下结论, 如图17所示。

图17 不同夹角下15 kHz三面角反射器目标强度随入射角变化曲线

1) 正交角三面反射器目标强度值在相同入射条件下大于非正交三面角反射器, 90°正交角反射器目标强度值比85°二面角反射器大3 dB;

2) 正交三面角反射器散射宽度优于非正交角反射器, 在入射角为25°～65°范围内具有较强的目标强度;

3) 正交三面角反射器随入射波角度改变目标强度变化较小, 稳定性强, 80°非正交角反射器则波动性极大, 无明显变化特征。

由上述分析可知, 在相同结构和流体材料属性及入射声源条件下:

1) 正交角反射器的声散射特性优于非正交角反射器, 角反射器板间夹角增大, 目标强度与散射宽度急剧减小;

2) 正交二面角反射器目标强度大于正交三面角反射器, 但散射宽度略小。

图18 86°～90°二面角反射器目标强度随入射角变化曲线

4 结论

针对水下弹性非正交角反射器的特点, 运用结构有限元+流体边界元的方法, 结合仿真软件ANSYS与SYSNOISE对非正交角反射器的声散射特性进行了仿真, 对非正交弹性二面角反射器与非正交弹性三面角反射器的散射声场进行仿真分析, 得到以下结论:

1) 正交角反射器声散射特性强于非正交角反射器;

2) 水下角反射器目标强度变化随着入射波频率的增加而增大, 且最大值出现在入射角度为45°附近;

3) 相同几何尺寸下二面角反射器声散射特性更强, 目标强度值大于三面角反射器, 散射宽度略小于三面角反射器;

4) 二面角反射器加工误差控制在2°以内时, 角反射器声散射特性并不会发生较大变化, 且2°的误差相比于绝对垂直, 更容易实现生产加工, 具有较为重要的实际意义。

受篇幅所限, 文中仅对弹性二面角与三面角反射器的非正交形态进行了分析, 对于刚性情况下非正交夹角的角反射器, 异型面构成角反射器仍需进一步研究。

[1] 汤广富, 李华, 甘荣兵, 等.海战场环境下角反射器干扰分析[J].电子信息对抗技术, 2015, 30(5): 39-45, 84.

Tang Guang-fu, Li Hua, Gan Rong-bing, et al.Analysis of Corner Reflector Under Naval Battle Field[J].Electronic Warfare Technology, 2015, 30(5): 39-45, 84.

[2] 张志远, 赵原源.新型二十面体三角形角反射器的电磁散射特性分析[J].指挥控制与仿真, 2018, 274(4): 138- 142.

Zhang Zhi-yuan, Zhao Yuan-yuan.Analysis of Electromagnetic Scattering Characteristic for New TypeIcosahedrons Triangular Trihedral Corner[J].Command Control & Simulation, 2018, 274(4): 138-142.

[3] 赵虎辰.一种X波段全向雷达角反射器阵列设计[J].河北省科学院学报, 2019, 36(1): 30-33.

Zhao Hu-chen.Design of an X-Band Omnidirectional Radar Angular Reflector Array[J].Journal of the Hebei Academy of Sciences, 2019, 36(1): 30-33.

[4] 徐海珠, 袁延艺, 刘雄厚, 等.线阵声诱饵对抗智能鱼雷尺度识别效果分析[J].舰船科学技术, 2017, 39(5): 135-138.

Xu Hai-zhu, Yuan Yan-yi, Liu Xiong-hou, et al.On Performance Analysis of Linear Array Decoy in Confronting Smart Torpedo[J].Ship Science and Technology, 2017, 39(5): 135-138.

[5] 陈建青, 赵俊杰.一种尺度目标模拟器的模拟逼真度分析[J].鱼雷技术, 2014, 22(6): 442-446.

Chen Jian-qing, Zhao Jun-jie.Fidelity Analysis of a Scale Target Simulator[J].Torpedo Technology, 2014, 22(6): 442-446.

[6] 罗祎, 文无敌, 陈鑫．一种水下目标尺度特征无源模拟优化方法[J]．海军工程大学学报, 2018, 30(1): 98-102．

Luo Yi, Wen Wu-di, Chen Xin.A Passive Simulating Optimization Method of Measure Characteristic of Underwa- ter Object[J].Journal of Naval University of Engineering, 2018, 30(1): 98-102．

[7] 毕亚峰, 贾晗, 杨军.基于变换声学的角反射器的设计[J].应用声学, 2019, 38(1): 52-57.

Bi Ya-feng, Jia Han, Yang Jun.The Design of Acoustical Corner Reflector Based on Transformation Acoustics[J].Applied Acoustics, 2019, 38(1): 52-57.

[8] 张小凤, 赵俊渭, 王尚斌, 等.水下物理目标声反射器研究[J].兵工学报, 2004, 25(5): 600-603.

Zhang Xiao-feng, Zhao Jun-wei, Wang Shang-bin, et al.A Study on Underwater Passive Sound Reflectors[J].Acta Armamentarii, 2004, 25(5): 600-603.

[9] 魏克难, 李威, 雷明, 等.基于耦合边界元法的水下目标低频声散射特性[J].舰船科学技术, 2014, 36(10): 32- 36.

Wei Ke-nan, Li Wei, Lei Ming, et al.The Low-frequency Acoustic Scattering Characteristics Study on Underwater Targets by the Coupled Boundary Element Method[J].Ship Science and Technology, 2014, 36(10): 32-36.

[10] Zeidan N I.GNSS Receivers for Weak Signals[A].The GNSS Technology and Applications Series[M].1rd ed.London, UK: Artech House, 2006.

[11] 陈鑫, 罗祎.水下刚性角反射器散射特性[J].声学技术, 2019, 38(3): 278-283.

Chen Xin, Luo Yi.Acoustic Scattering Characteristics of Underwater Rigid Corner Reflector[J].Technical Acoustics, 2019, 38(3): 278-283.

[12] 陈鑫, 罗祎, 李爱华.水下弹性角反射器声散射特性[J].兵工学报, 2018, 39(11): 2236-2242.

Chen Xin, Luo Yi, Li Ai-hua.Acoustic Scattering Characteristics of Underwater Elastic Corner Reflectors[J].Acta Armamentarii, 2018, 39(11): 2236-2242.

Analysis of Acoustic Scattering Characteristics of Underwater Non Orthogonal Acoustic Corner Reflectors

XIE Tao-tao, LUO Yi, XIAO Da-wei

(College of Weaponry Engineering, Naval University of Engineering, Wuhan 430033, China)

Underwater corner reflectors possess strong far-field acoustic scattering characteristics, and because of the assembly error, the standard orthogonal metal corner reflector cannot meet the absolute vertical of each plate.The production error is an important factor that affects the sound scattering characteristics of corner reflectors.The acoustic scattering characteristics of non-orthogonal corner reflectors were studied.The pinch theorem idea was used to change the angle between standard corner reflectors (90°, 85°, and 80°), and a qualitative analysis was performed.The structural modeling software ANSYS was used to model and mesh the non-orthogonal dihedral and trihedral corner reflectors.The acoustic simulation software SYSNOISE was used to analyze the acoustic scattering characteristics of non-orthogonal dihedral and trihedral corner reflectors.Furthermore, far-field acoustic scattering characteristics were simulated and analyzed by the structural finite element and fluid boundary element methods.The acoustic scattering characteristics were compared with standard orthogonal corner reflectors under similar loading and acoustic field conditions.The acoustic scattering intensity of the target under different incident angles of sound waves and variation law of the target intensity with the frequency of the incident sound waves were obtained.The results showed that the acoustic scattering characteristics of orthogonal corner and orthogonal dihedral corner reflectors were better than those of non-orthogonal corner and trihedral corner reflectors, respectively.The production error of the dihedral corner reflector was less than 2° and will not have a substantial impact on the acoustic scattering characteristics.

underwater corner reflector; production error; structural finite element method; fluid boundary element method; acoustic scattering; target strength

谢涛涛, 罗祎, 肖大为.水下非正交声学角反射器声散射特性研究[J].水下无人系统学报, 2022, 30(1): 94-101.

TJ630; TB566

A

2096-3920(2022)01-0094-08

10.11993/j.issn.2096-3920.2022.01.012

2020-08-14;

2021-03-29.

谢涛涛(1995-),男, 硕士, 主要研究方向为兵器工程.

(责任编辑: 杨力军)