考虑混合信息表征和属性交互的目标导向新产品开发方案选择方法
2022-03-15张新卫同淑荣
张新卫, 李 靖, 冯 琼, 同淑荣
(西北工业大学 管理学院,陕西 西安 710072)
0 引言
目标值表示一项决策目标或属性被期望达到的水平,是个人和组织决策中的重要影响因素[1,2]。在一些产品选择决策中,顾客不仅会考虑产品属性值的绝对水平,而且会考虑属性值达成目标值的相对水平。将目标值融入到基于产品属性的方案选择中,考虑属性值达成目标值的情况,对于企业选择更具比较优势的产品开发方案具有重要意义。
针对目标导向的产品开发方案评价或选择问题,国内外学者已做了相应研究,主要分为基于前景理论(或累积前景理论)和基于目标导向决策分析的方案选择。基于前景理论的方案选择考虑了产品属性值与参照点之间的相对关系,以及决策者的行为,例如,参照点依赖、损失规避和敏感性递减等。姜艳萍等通过比较新产品开发方案与竞争产品绩效确定了前景参考点,提出基于前景理论的新产品开发方案选择方法[3]。在考虑群体参照点情况下,张晓等提出基于前景理论的多属性决策方法,用于设计方案的评价[4]。Ying等基于累积前景理论和混合信息多属性决策方法提出了新产品概念的选择方法[5]。在基于目标导向决策的产品方案选择方面,决策者的效用依赖于属性值是否达成目标值。在目标值表示为概率密度时,Bordley等提出目标导向的多属性偏好分析方法,并用于大型集成电路测试仪的方案评价[1]。在属性值和目标值均表示为语言值时,Yan等利用模糊目标导向的决策分析,结合优先集成算子对手工艺品进行感性评价[6]。围绕决策者对目标值的不同偏好类型,Yan等基于Choquet积分和λ模糊测度提出模糊目标导向的非可加多属性决策分析方法,并与Bordley等的方法进行比较[7]。此外,目标导向决策分析也被用于服务设计等[8]。Bordley等指出,目标导向的多属性偏好函数与多属性效用函数具有战略等价性;同时,目标导向的方法对于产品开发和环境管制等问题是更加自然的选择[1]。
在基于目标导向决策分析的方案选择中,对混合信息表征的目标值考虑还较少。然而,在新产品开发中,属性值和目标值往往具有不确定性,可能表示为清晰数、区间值、语言值和概率密度等形式,导致混合信息表征广泛存在。有必要将混合信息表征的属性值和目标值进行统一化表示,进而计算目标达成概率。另外,产品多属性之间通常存在交互。然而,在目标导向决策研究中,提出需要评定2n(n为属性个数)个参数以决定多属性偏好函数,导致属性个数多时参数评定十分困难[1]。在产品开发方案评价中,或是不考虑属性交互并采用线性加权的方式,或是利用λ模糊测度仅考虑属性之间的一类交互作用,即正交互或负交互,使得评价结果产生偏差[7]。因此,属性交互的建模和分析应在准确性和复杂性之间取得平衡,在此基础上进行各属性目标达成概率的集结。
针对目标导向的新产品开发方案选择问题,考虑属性值和目标值表示为清晰数、区间值、模糊数、语言值或概率密度的情形,将区间值、模糊数或语言值表示的属性值和目标值统一转化为概率密度,结合决策者对属性的效益型、成本型和固定型偏好,利用目标导向的决策分析方法评定目标达成概率。在此基础上,针对属性交互,以及k-可加模糊测度在建模属性交互时具有柔性和准确性的特点[9,10],利用k-可加模糊测度和Choquet积分对各属性的目标达成概率进行集结。最后,以集成电路测试仪的方案评价为例,开展应用研究。
1 问题描述
设A={a1,…,ai,…,am}为新产品开发方案集,其中ai表示第i个方案;X={X1,…,Xj,…,Xn}为方案属性集,其中Xj表示第j个属性;X′=(xij)m×n为决策矩阵,其中xij表示第i个方案的第j个属性值;T={t1,…,tj,…,tn}为目标值集,其中tj表示第j个属性的目标值;pij(xijtj)表示xij达成tj的概率。
由于新产品开发过程的复杂性和不确定性,xij和tj往往具有模糊性和不确定性,可以具有不同表达形式,例如,清晰数、区间值、概率密度、模糊数和语言值等。决策者对不同属性具有不同的偏好类型,包括效益型偏好,成本型偏好和固定性偏好。同时,多属性之间往往存在交互,其交互类型可以是互补或替代交互,并且交互强度不一。
本文的研究问题是:在考虑xij和tj的混合信息表征以及属性的不同偏好类型基础上,如何计算xij满足tj的概率pij(xijtj);并在考虑属性交互的情况下,如何获取方案ai达成T的程度,进而支持不同产品开发方案的排序和选择。
2 理论基础
2.1 目标导向决策分析
目标导向决策分析认为,当属性值xij确定能达成目标值tj时,xij的效用为1;当xij确定不能达成能tj时,xij的效用为0;当xij能否达成tj不确定时,xij的期望效用v(xij)可以通过属性值达成目标值的概率衡量[1]:
(1)

在期望效用理论中,xij的期望效用通过公式(2)衡量:
(2)
2.2 模糊测度和Choquet积分
定义1[10]设X={X1,…,Xj,…,Xn}为属性集,P(X)为X的幂集,若集函数μ:P(X)→[0,1]满足如下条件:(1)μ(Ø)=0,μ(X)=1;(2)对任意的S,Q⊆X,S⊆Q⟹μ(S)≤μ(Q)。则称μ为定义在P(X)上的模糊测度。其中,μ(Xj)表示{Xj}本身的重要程度;μ(S)和μ(Q)分别表示属性集S和Q的重要程度。
定义2[10]对任意Q∈P(X),μ(Q)的默比乌斯变换可定义为:
(3)
其中,|Q|和|S|分别代表属性集S和Q的势。
μ(Q)和mμ(Q)之间能够相互转换。对任意Q∈P(X),μ(Q)可由默比乌斯表达式表示:
(4)
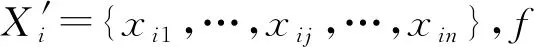
(5)
其中,下标(j)表示在f(xij)上的排序,使得f(xi(1))≤f(xi(2))≤…≤f(xi(n));Q(j)={X(j),X(j+1),…X(n)};Q(n+1)=Ø。

(6)
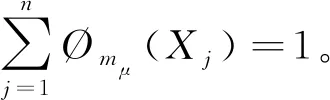
(7)
属性之间的交互程度通过交互指数进行衡量。基于默比乌斯变换的属性Xi和Xj的交互指数表示为[10]:
(8)
为了减轻决策者评定模糊测度μ的工作量,Grabisch提出了k-可加模糊测度。
定义4[10]对任意的k∈{1,…,n},任意的Q,S∈P(X),|Q|>k,|S|=k,若满足mμ(Q)=0并且存在至少一个S满足mμ(S)≠0,则模糊测度μ是k-可加模糊测度。
3 基于目标导向决策和k-可加模糊测度的新产品开发方案选择方法
3.1 方法框架
针对新产品开发方案中属性值和目标值的混合信息表征,将不同的表达形式都转化为概率密度。在考虑属性的效益型偏好、成本型偏好和固定型偏好基础上,利用目标导向决策分析对各个属性值满足目标值的程度进行概率衡量。
在给定属性交互方向或强度,属性总体重要度等信息的条件下,利用最小方差方法进行k-可加模糊测度的识别。以目标达成概率和模糊测度为输入,利用Choque积分算子进行非可加集成,并计算Choquet积分值作为方案排序和选择的标准。提出基于目标导向决策和k-可加模糊测度的新产品开发方案选择框架,如图1所示。

图1 基于目标导向决策和k-可加模糊 测度的新产品开发方案选择框架
3.2 评价方法的步骤
(1)新产品开发方案信息的确定。在方案评价之前,需要确定可行的方案集A={a1,…,ai,…,am},属性集X={X1,…,Xj,…,Xn},以及各个方案的属性值xij,并构建决策矩阵X′=(xij)m×n。对于属性集X={X1,…,Xj,…,Xn},需要识别对应的目标值集T={t1,…,tj,…,tn}。

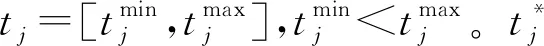
当tj为模糊数时,表示Xj的目标值信息外延模糊,没有精确含义,并通过具有隶属函数的模糊子集表示,tj的一般形式可表示为[7]:
(9)


(10)

当tj为语言值时,表示Xj的目标值是模糊数,具有语言形式。不失一般性,设tj∈L,L={lp|p=0,1,…,E},L表示包含E+1个语言值的语言值集,E通常为偶数,lp表示语言值。例如,某一语言值集{很好,好,中,差,很差}由“很好”、“好”等5个语言值组成。为了方便计算,通常将语言值lp转化为三角模糊数。lp的三角模糊数表示和对应的概率密度表示可分别由等式(9)和等式(10)获得。
(3)三种属性偏好下目标达成概率的衡量。在三种不同的属性偏好下,目标达成概率pij(xijtj)的衡量需要采用不同的计算方法。此外,经过步骤(2)的转化过程,属性值和目标值均可用清晰数或概率密度表示。因此,在每一种属性偏好下,属性值与目标值的比较存在4种情形:清晰数与清晰数、清晰数与概率密度、概率密度与清晰数、概率密度与概率密度之间的比较。
当决策者对属性具有效益型偏好时,属性值越大越好。pij(xijtj)变为pij(xij≥tj)。当xij与tj均为清晰数时,xij≥tj表示目标达成概率为1,反之,目标达成概率为0。当xij为清晰数,tj为概率密度时,pij(xij≥tj)表示为:
(11)
当tj为清晰数,xij为概率密度时,pij(xij≥tj)可表示为:
(12)
当xij与tj均表示为概率密度时,pij(xij≥tj)表示为:
(13)
当决策者对属性具有成本型偏好时,属性值越小越好。pij(xijtj)变为pij(xij≤tj)。当xij与tj均为清晰数时,xij≤tj表示目标达成概率为1,反之,目标达成概率为0。当xij为清晰数,tj为概率密度时,pij(xij≤tj)表示为:
(14)
当tj为清晰数,xij为概率密度时,pij(xij≤tj)表示为:
(15)
当xij与tj均表示为概率密度时,pij(xij≤tj)表示为:
(16)
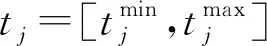
(17)
当tj为清晰数,xij为概率密度时,pij(xij≌tj)为pxij(tj)。当xij与tj均表示为概率密度时,pij(xij≌tj)表示为:
(18)
(4)k-可加模糊测度的识别。目前,关于模糊测度的识别方法包括最小方差法和最小二乘法等[10]。基于最小方差法的模糊测度识别需要的决策者偏好信息相对最小二乘法等要求低:该方法不需要决策者提供对方案的整体效用感知;只需提供属性之间的交互方向或交互强度、不同方案之间的排序、属性的整体重要度或排序等信息。因此,利用最小方差法进行k-可加模糊测度的识别,其最优化函数可表示为:
(19)
其中,限制中第1个不等式和第2个等式是k-可加模糊测度时mμ必须满足的条件。限制中的其余条件是可选条件,依赖于决策者给出的初始偏好信息:Cmμ(ai)-Cmμ(aj)≥δc表示方案ai比aj更优;Ømμ(Xi)-Ømμ(Xj)≥δφ表示属性Xi比Xj更重要;Imμ({Xi,Xj})≥δI或Imμ({Xi,Xj})≤-δI表示属性Xi和Xj之间的存在正交互或负交互;δc,δφ,δI分别表示决策者主观定义的非负无差异阈值。此外,还可添加属性总体重要度、属性交互强度等可选条件。实际上,通过该方法识别了μ的默比乌斯变换mμ,可利用等式(3)和(4)在mμ和μ之间进行相互转换。
(5) 新产品开发方案Choquet积分值的计算。基于弱可隔离公理,Krantz等提出了可分解模型[10]:u(x)=F(u1(x1),…,(un(xn))。其中,x=(x1,…,xn)∈X,ui(xi)单属性效用函数,F是集结函数。在考虑属性交互的情况下,基于模糊测度的Choquet积分集结算子是一种合适的集结函数,要求单属性效用函数ui(xi)之间是相称的[19]。属性的目标达成概率pij(xijtj)=ui(xi)都在[0,1]之间,并且不同属性的同一目标达成概率值具有一致的解释,满足相称性。因此,利用可分解模型和基于模糊测度的Choquet积分对不同属性的目标达成概率进行集结。
根据步骤3和4获得的信息,利用等式(5)对方案各属性值的目标达成概率进行集结,计算方案ai的Choquet积分值,公式如下:
(20)
其中,下标(j)表示在pij(xij≥tj),j=1,…,n上的排序,使得pi(1)(xi(1)≥t(1))≤pi(2)(xi(2)≥t(2))≤…≤pi(n)(xi(n)≥t(n));Q(j)={X(j),X(j+1),…,X(n)};Q(n+1)=0。
4 算例
4.1 方法应用
某公司开发了一种大规模集成电路测试装备的新方案a1(OR9000)[11]。相对于市场上已有测试装备a2(J941)和a3(Sentry50),该公司希望获得潜在工业顾客对a1的评价情况。通过信息收集,识别了技术(XT)、经济(XE)、软件(XS)和供应商支持(XV)等4大类评价指标,包括17个与测试装备相关的产品和服务属性。属性、属性权重、偏好类型和不同方案的属性值由文献[11]给出。
在该例子中,三个不同装备的属性值都是清晰数。目标值的设定依赖于市场上已有方案a2和a3的属性值。决策者可以将目标值设定为方案a2和a3在各属性的偏好最小值、偏好最大值或区间[min(x2j,x3j),max(x2j,x3j)]内的任一可能值。此时,可根据实际情况利用区间数、模糊数或概率密度表示目标值。例如,属性X1的目标值t1的一种模糊数表示是(96,256,256,256),则a1达成目标值t1的概率可用等式(11)计算:
(21)
各属性的模糊目标值和区间目标值如表1第3列和第4列所示。在模糊目标值下,a1,a2和a3三个方案的目标达成概率如表1第5列、第7列和第8列所示。在区间目标值下,a1,a2和a3三个方案的目标达成概率如表第6列、第7列和第8列所示。

表1 方案的目标达成概率
例子中有17个产品和服务属性,需要评定的模糊测度值有217=131072个。为了减少计算量,利用层次建模的思路,首先考虑技术、经济、软件和供应商支持4个指标内部属性之间的交互关系,并利用Choquet积分将指标内部的不同属性进行集结;然后,考虑4个指标之间的交互关系,并利用Choquet积分将4个指标进行集结。经过分析,决策者认为技术和经济指标之间存在补充交互,经济和软件指标之间存在补充交互,技术和软件指标存在替代交互;软件指标内部X11和X12,X13和X14之间存在替代交互。将所有识别的属性交互关系用等式(8)进行表示,并将决策者评定的各个属性权重作为Shapley值,进而利用等式(19)求得模糊测度μ的默比乌斯变换mμ。
当k=2时,4个指标对应的μ,mμ和Imμ如表2所示。在2可加模糊测度下,三个指标及以上的Imμ以及mμ均是0;两个指标之间的Imμ以及mμ相等。当指标集仅包含单个指标时,可得mμ=μ,且Imμ与Shapley值相等。同时,由于指标之间存在交互,单个指标的μ值与Imμ不一致。

表2 当k=2时指标集的模糊测度、默比乌斯变换和交互指数
通过等式(20)对3个方案进行基于Choquet积分的多指标集结,计算Choquet积分值。在2可加模糊测度下,当目标值为选定的模糊值时,Cμ(a1)=0.587;Cμ(a2)=0.591;Cμ(a3)=0.8。当目标值为满足一致分布的区间值时,Cμ(a1)=0.64;Cμ(a2)=0.591;Cμ(a3)=0.8。通过以上分析,可以得到该公司开发的方案a1明显劣于市场上的方案a3;a1是否优于市场上的方案a2取决于目标值的不同信息表征及其对应的概率密度。因此,为了提高装备的竞争力,应停止对a1继续进行开发,或者需要会对a1进行改进。当k=1,3,4时的评价结果如表1所示。
4.2 比较和分析
Bordley等提出了目标导向的多属性偏好分析方法,并将方法用于该算例[1]。其研究利用市场上的方案a2和a3的属性值设定目标值,并且目标值被设定为清晰数。其中,效益型属性的目标值定义为tj=max(x2j,x3j),成本型属性的目标值定义为tj=min(x2j,x3j)。当a1的属性值x1j优于目标值时,目标达成概率为1;反之,目标达成概率为0。例如,方案a2和a3在引脚能力X1的属性值分别是96和256。由于X1是效益型属性,因此,目标值设定为256。同时,由于x11=160<256且x21=96<256,因此,方案a1和a2的目标达成概率都是0。各个方案的目标达成概率见表1的第10列、第11列和第12列。在此基础上,Bordley等利用线性加权集成计算方案a1、a2和a3的价值,分别是0.514,0.584和0.82。
然而,该属性的偏好类型是单调递增的,属性值160的效用在一定程度上应大于96的效用,并且目标值也并不必须固定在256。本文将Bordley等的目标设定方法一般化,目标值可以表示为区间值、模糊值和概率密度等形式,并且可以区分不同属性值的不同目标达成概率,例如,在目标值是区间值且满足一致分布时,属性值160的目标达成概率是0.4,而属性值96的目标达成概率是0。同时,在考虑属性交互的情况下,利用k-可加模糊测度和Choquet积分对目标达成概率进行集结。属性独立下的线性加权集成是k-可加模糊测度和Choquet积分的特殊化,即k=1的情形。因而,本文的方法比线性加权集成更具一般性,能够对属性交互进行准确和柔性地建模。
5 结论
本文提出一种考虑混合信息表征和属性交互的目标导向的新产品开发方案选择方法。在新产品开发中,属性值和目标值存在不确定性,导致属性值和目标值由清晰数、区间值、模糊值和语言值等混合信息表征。为此,将由区间值、模糊值、语言值表示的属性值和目标值统一表示为概率密度。结合属性的三种偏好,计算目标达成概率,并作为单属性效用的衡量。针对属性交互的问题,在识别属性交互方向或强度、属性重要度或排序、部分方案排序等信息下,利用最小方差法识别k-可加模糊测度,并利用Choquet积分对目标达成概率进行集结。将方法用于大型集成电路测试仪的开发中,并与已有研究成果开展比较和分析,验证了方法的有效性。方法具有以下特点:(1)将混合信息表征的属性值和目标值表示为清晰数或概率密度,并衡量属性值达成目标值的概率,是一种基于概率的方法;(2)目标达成概率属于[0,1],确保了不同目标达成程度的可比较性,避免了归一化的需求;(3)基于k-可加模糊测度和Choquet积分能够考虑k个属性之间的交互及其交互强度对方案评价的影响,比线性加权集结具有更高的准确度和柔韧性。
