考虑n中连续取k失效准则的树状系统可靠性求解方法

2022-03-15崔利荣

运筹与管理 2022年2期

杨奥, 崔利荣

(1.中国航空综合技术研究所,北京 100028; 2.青岛大学质量与标准化学院,山东青岛 266071)

0 引言

自20世纪50年代可靠性科学诞生起，可靠性理论飞速发展，对航空、航天、军事、能源等重大工程的发展起到了不可替代的作用[1]。同时，随着可靠性理论的发展，可靠性模型分析方法也发展众多，但随着系统可靠性模型越来越复杂，传统方法如组合法、全概率公式法、递推方程法和矩生成函数法等在系统可靠性评估与分析中往往效率不高[2]，给系统可靠性评估和系统可靠性分析带来了一定的困难。

在20世纪90年代Fu和Koutras[3]提出有限马尔可夫嵌入法一度成为计算系统可靠性研究热点。该方法可作为解决系统可靠性评估、部件重要度分析、故障率函数计算和新可靠性试验分析的优秀工具[4]。如Koutras[5]、赵和崔[6]等人均利用该方法解决了许多与可靠性相关的问题，尤其对于复杂冗余系统可靠性求解，有限马尔可夫嵌入法已取得较为广泛的应用。

另一方面，网络系统作为系统可靠性研究领域中的重要分支，一直被各路学者广泛关注。XingLiu-dong曾多次讨论多阶段系统[9,10]和网络系统可靠性[9,10]，马洪伟[11]研究了随机交通网络的网络渐进联通可靠性。吕靖[12]则引入不确定变量研究了原油海运网络连通可靠性。或者将网络系统可靠性作为优化问题的优化要素，如吕彪[13]研究了考虑路网可靠性和空间公平性的次优拥挤收费模型。树状系统作为网络系统中的一部分在生活中随处可见，如运输系统，网络信息传输，中央仓库分货系统等。但现阶段关于网络可靠性研究较少，其中日本研究员Aki曾在1999年[14]和2016年[15]分别发表论文探究用游程及概率母函数法求解树状系统，但该方法要求各网络节点工作概率相同，具有一定实际应用的局限性。因此，结合现阶段在系统可靠性应用广泛的有限马尔可夫嵌入法，本文提出基于变形有限马尔可夫嵌入法的n中连续取k树状系统可靠性求解方法。填补这一研究领域空白。

1 树状系统建模

现阶段关于树状系统可靠性研究通常从确定图入手，如Aki[14]。但针对确定的树状系统可靠性求解难以进行算法复杂度分析，同时无法对随机树系统进行有效的可靠性求解。因此本文给出一种更一般的树状图表示形式。

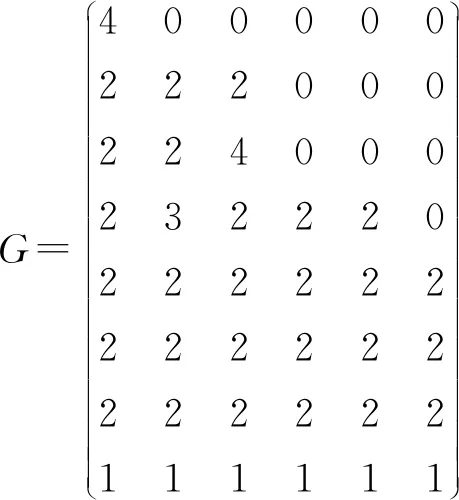
设T为一有向树，V为节点向量，表示T中全部节点，树中节点按层序遍历编号，vi表示其中编号为i的节点。定义树T包含三类参数：树T的层数l；层-节点向量A=[a1,a2,…,al]1×l，其中，aj表示第j层节点总数，a1通常取1；父-子节点矩阵Gl×max{A}，其中G(α,β)=k表示第α层第β个节点共有k-1个子节点，其中，对于矩阵第l行有

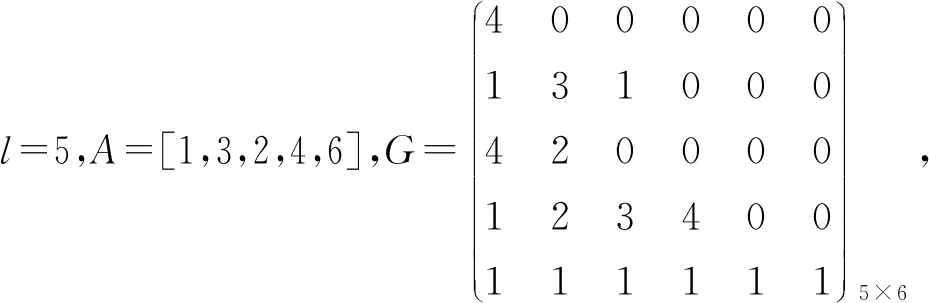
图1 树T1示意图

现讨论给定树Tn上任一节点vt的子节点搜索模式。

设ch(vt)={vt1,vt2,…vtz}表示vt的子节点集合。若G(αt,βt)=1，则vt为叶节点(子节点数为0)；若G(αt,βt)≠1有

(1)

(2)

通过公式(1)与公式(2)可确定任一给定节点vt的子节点集合ch(vt)。因此，按本文树状图定义模式可实现节点定位及子节点查找。现讨论递归树形式。

定义1对于确定树Tn(l,A,G)以其中任意一非叶节点vt开始及延其传播方向上全部节点组成的树状结构称为Tn的子树，记作subTn(vt)，其中vt为subTn(vt)的根节点。若vt为叶节点subTn(vt)为叶节点本身。

定义2树Tn(l,A,G)的根节点为vk，vk的子节点分别为vk1,vk2,…,vkz。利用1中子树定义，将树Tn(l,A,G)表示为:

Tn(vk)={vk|subTn(vk1),subTn(vk2),…,subTn(vkz)}

(3)

因此，利用式(3)对子树进行表示，可得到树的递归形式。

以树T1为例。用递归形式表示树T1。

T1={v1|subT1(v2),subT1(v3),subT1(v4)}；

subT1(v3)={v3|subT1(v5),subT1(v6)}；

subT1(v5)={v5|subT1(v7),subT1(v8),subT1(v9)}；

subT1(v6)={v6|subT1(v10)}；

subT1(v8)={v8|subT1(v11)}；

subT1(v9)={v9|subT1(v12),subT1(v13)}；

subT1(v10)={v10|subT1(v14),subT1(v15),subT1(v16)}

2 树状系统可靠性求解

根据第1节定义，若存在一有向树T，且T上任一节点vt(1≤t≤sal)处存在唯一二元部件Xt与之对应，则称由全体Xt组成的系统为树状系统，记作Tsys(X[1,sal])，其中X[1,sal]为树状系统中全部部件组成的集合。

常见的系统失效形式有以下几种:

1)n中连续取k失效准则：当系统中存在连续k个或k个以上部件失效时，系统被视为失效。

2)n中取k失效准则：当系统中存在k个或k个以上部件失效时，系统被视为失效。

3)(n,f,k)失效准则：当且仅当在系统中有f或f以上个单元失效或有连续k个或连续k个以上部件失效时，系统被视为失效。

本文主要对第一种失效形式展开讨论。其中，对于树状系统sal中连续取k失效准则要求失效零部件分布满足有向树传播方向。以第1节树T1为例，给出一种T1-sys(X[1,16])连续取k(k=3)连续失效示意图，如图2所示。其中，“●”表示部件失效。

图2 一种T1-sys(X[1,16])失效模式

现讨论在给定失效准则下树状系统sal中连续取k可靠性计算公式。

考虑sal个单元1,2,…,sal组成的一个树状可靠性系统。假设每个单元假设每个单元有两种状态：工作状态和失效状态。系统的状态完全取决于它的单元的状态，因此系统共由2sal种可能的状态。根据可靠性系统的特点，定义一个齐次马尔可夫链{X(t),t=0,1,…}，再将系统可靠性问题转化为马尔可夫链的问题，依据马尔可夫链的已知结果，给出可靠性问题的结果。其中对于线性系统，已有学者利用马尔可夫嵌入法给出可靠性计算方法。

对于一个由n个单元组成的线性系统X，给定参数k及各单元在马尔可夫链上的一步转移概率pij(t)=P{X(t)=j|X(t-1)=i}(1≤i≤n)，构造相应的转移概率矩阵Λ(t)=(pij(t))(k+1)×(k+1)，其中p(k+1)j=0,(j≠k+1),p(k+1)(k+1)=1。因此，得到嵌入马尔可夫链的可靠性系统的一般公式[2]为

(4)

其中，π=(π0,π1,…,πk)1×(k+1)表示该马尔科夫链的初始概率，向量U的作用是将系统处于工作状态的概率进行求和，从而得到系统可靠度。通常对于一个新系统，π=(1,0,…,0)；U=(1,1,…,1,0)1×(k+1)。

将(4)式第一项展开，

(5)

设Am=[0,0,…,1,0,…,0]1×(k+1)，其中第m项为1(1≤m≤k+1，余下同)，Am表示系统初始状态向量。

(5)式可改写为

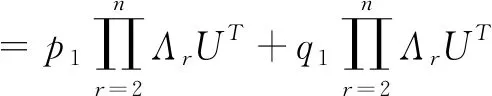
(6)

因此，(6)式可改写为

Rsys(X,k)=R1(X[1,n],k)

=[p1,q1][R1(X[2,n],k),R2(X[2,n],k)]T

(7)

式(7)表明系统X[1,n]可靠度可拆解为X1部件状态向量与X[2,n]系统与对应的状态可靠度的内积。将(7)式推广到一般，对n中连续取k失效准则，若给定线性系统X[i,j]初始状态为m及参数k有系统可靠度为

Rm(X[i,j],k)

=[pk,qk][R1(X[i+1,j],k),Rm+1(X[i+1,j],k)]T

(8)

式(8)称作线性系统可靠性迭代公式。将其推广到树状系统。对于树状系统，在父节点状态确定的条件下，子节点状态相互独立，即子树系统状态相互独立。因此，树状系统可靠度可表示为根节点部件的状态向量与余下子树系统可靠性的积。

设存在一树状系统Tsys(X[i,j])，其中，Xi为树的根节点处部件。Rm(Tsys(X[i,j]),k)表示树状系统Tsys(X[i,j])在给定参数k及初始状态为m的可靠度，有

Rm(Tsys(X[i,j]),k)

(9)

其中，Rm(subT(Xr),k)，表示以vr为根节点所构成的子树系统，且当前状态m时的系统可靠度。当树状系统为线性系统时式(4)依然成立。特别地，当子树系统为叶结点时，即subT(Xlf)=Xlf，有

(10)

其中，对于任意系统X，当m=k+1时

Rm(X,k)=0

(11)

对于系统X层数lX，当lX满足lX+m≤k时

Rm(X,k)=1

(12)

综上，利用树状系统迭代公式(9)与式(4)、式(10)、式(11)与式(12)可对任意树状系统连续取k模型进行可靠性计算。下文给出数值算例。

3 数值算例

本章通过几类典型例子对算法应用加以说明。

3.1 完全树系统

完全树系统是部件排布满足完全树形式的可靠性系统。现给出一完全二叉树系统T2(l,A,G)，其中l=5，A=[1,2,4,8,16]

有树T2如图3所示。

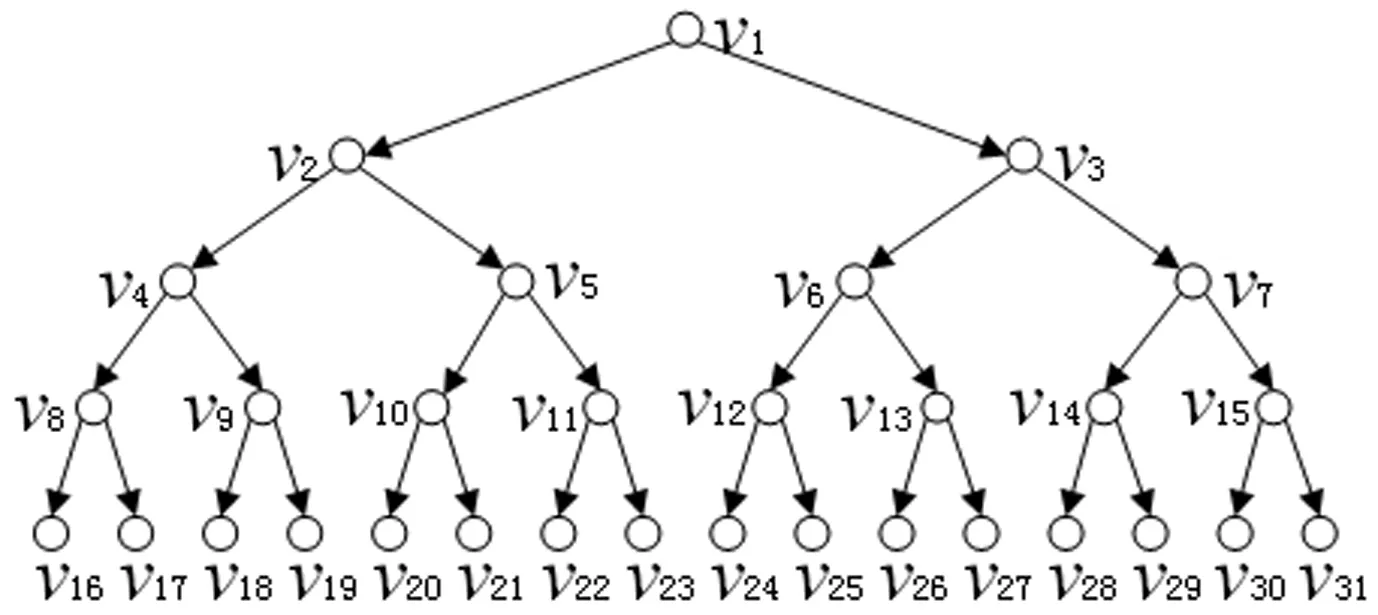
图3 完全树系统T2示意图

其中，对于部件Xi(1≤i≤31)，有工作状态概率为pi=1-0.01i，给定初始状态m=1，k=4，利用第2节公式可得树状系统T2的系统可靠度为

R1(Tsys(X[1,31]),4)

由于subT(X2)与subT(X3)结构完全一致，因此仅对subT(X2)的可靠性展开求解。现直接给出可靠度计算结果，其中，第四层全部节点为根节点的子树系统可靠度如表1所示。

表1 第四层全部节点为根节点的子树系统可靠度

利用表1数据计算以第三层全部节点为根节点的子树系统可靠度，如表2所示。

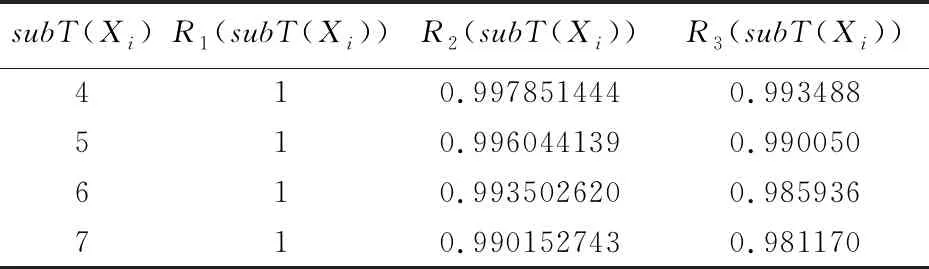
表2 第三层全部节点为根节点的子树系统可靠度

利用表2数据继续计算得到以第二层全部节点为根节点的子树系统可靠度，有

R1(subT(X2),4)=0.999878081637186
R2(subT(X2),4)=0.999672055888000
R1(subT(X3),4)=0.999511580343489
R2(subT(X3),4)=0.999021124753600

因此，树状系统T2系统可靠度为

R1(Tsys(X[1,31]),4)

=0.999382759329300

3.2 长链条系统

长链条系统是指包含多个子树为线性系统的树状系统，一般常见于管道运输，微波信号传输等系统。现给出一树状系统T3(l,A,G)，其中l=8，A=[1,3,3,5,6,6,6,6]

树T3如图4所示。

图4 T3长链条系统示意图

其中，对于部件Xi(1≤i≤36)，有工作状态概率为pi=1-0.01i，给定初始状态m=1，k=5，有树状系统T3的系统可靠度为

R1(Tsys(X[1,36]),5)

其中，对于子树系统subT(X2)为线性系统，因此可直接利用公式(4)计算出系统可靠度。现直接给出可靠度计算结果，其中，subT(X14)和subT(X15)系统可靠度如表3所示。

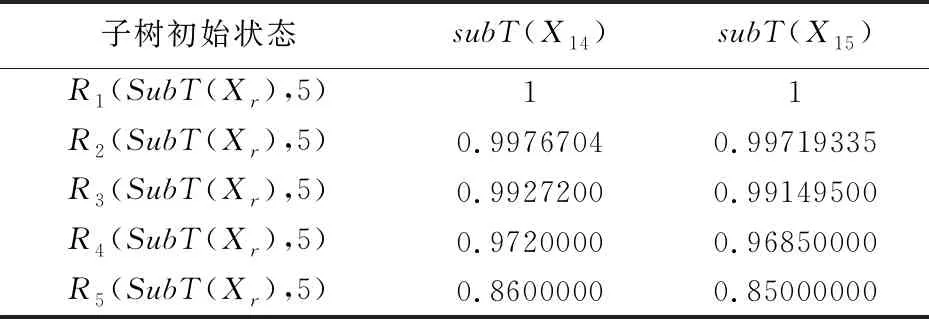
表3 subT(X14)和subT(X15)系统可靠度

迭代计算得

R1(subT(X3),5)=0.999474172768361,
R2(subT(X3),5)=0.999440090884361

同理可计算出

R1(subT(X4),5)=0.998471715071798,
R2(subT(X4),5)=0.998353251697900

因此，树状系统Tsys(X[1,36])系统可靠度为

R1(Tsys(X[1,36]),5)=0.997773770874255

3.3 一般(随机)树系统

一般树系统又称随机树系统，即通过生成随机树的方式生成树状系统。本文生成一随机树T4(l,A,G)，其中l=8，A=[1,3,7,11,9,7,1,1]

有树T4如图5所示。

图5 T4随机树系统示意图

其中，对于部件Xi(1≤i≤40)，设工作状态概率为pi=1-0.01i。给定初始状态m=1，k=3。直接给出树状系统T4的系统可靠度为

R1(Tsys(X[1,40]),3)=0.793062318995683

4 讨论

4.1 算法复杂度分析

本章对本文提出的算法运算复杂度进行分析，即考虑在给定树状系统结构参数G和失效准则参数k下算法需要进行的加法运算次数与乘法运算次数。

将公式(9)展开得

Rm(Tsys(X[i,j]),k)

(13)

定义矩阵内元素求和函数sum(·)。其中，sum(N)=n，表示对矩阵N内非零元素求和，求和结果为n。

定义矩阵内非零元素个数和函数count(·) 。其中，count(N)=c，表示对矩阵N内非零元素个数求和，矩阵非零元素个数和为c。

由式(13)可知，计算Rm(Tsys(X[i, j]),k)时需进行2·(iq-i1)次乘法运算，1次加法运算。当给定失效准则参数k(k≥1)时，由式(12)可知，对一般树状系统需对式(13)计算k次(m分别取1,2,…,k)。因此，由G′可知，对于树状系统Tsys(X[1,sal])求解可靠度时需进行2k·sum(G′)次乘法，k·count(G′)次加法。即算法乘法复杂度为O(2k·sum(G′))；加法复杂度为O(k·count(G′))，分别为子节点数量矩阵G′和失效准则参数k的线性阶。

以图5中树T4为例，有

其中，sum(G′)=39;count(G′)=20。因此，对于给定k=3，利用本文算法计算由T4组成的树状结构可靠度需进行2×3×39=234次乘法运算；3×20=60次加法运算。

现讨论两类特殊树状系统：线性系统与完全h叉树系统。

对于线性系统，有sum(G′)=l-1；count(G′)=l-1。因此，对于给定k有线性系统算法乘法复杂度：O(2k(l-1))；加法复杂度：O(k(l-1))。

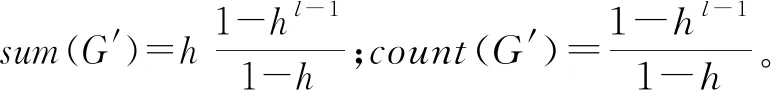
4.2 算法对比

现阶段关于树状系统可靠性的研究较为有限，其中日本学者Aki[14]用条件概率母函数法成功求解了树状系统连续取k失效准则和(n,f,k)失效准则。在此本文针对n中连续取k失效准则，对Aki提出的算法与本文算法进行对比。

本文引用Aki 1999年论文[14]中所构造的树状的系统，设存在一树状系统T5(l,A,G)，其中l=4,A=[1,3,6,8]

有树T5如图6所示。

图6 树状系统T5示意图

设给定系统中零件工作概率pi=p(1≤i≤18)，失效准则参数k=3。分别采用本文算法和条件概率母函数法对树状系统T5的可靠性进行求解，结果如表4所示。

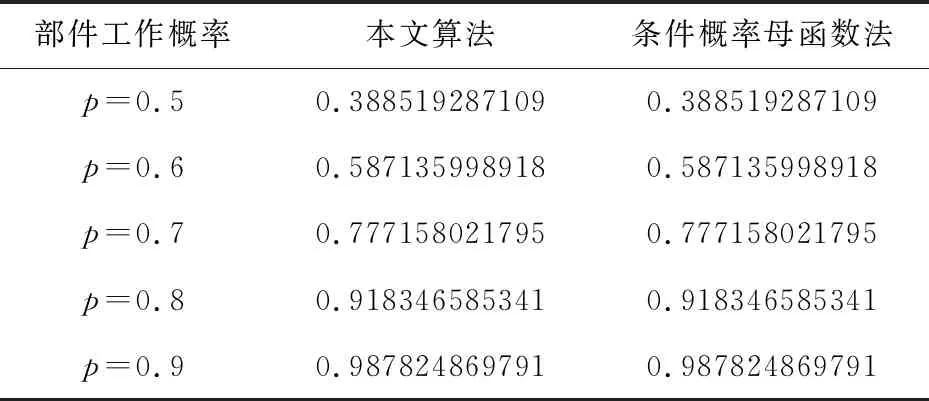
表4 部件工作概率为p时两类算法计算系统可靠度

由表4可以看出，本文算法与条件概率母函数法在求解树状系统连续取k可靠度问题上结果完全一致，从侧面印证了本文算法的正确性。现在从算法复杂度和算法适用情况两个方面讨论此两种算法的使用效果。

算法复杂度方面，本文算法运算复杂度在第4.1小结中已有讨论，乘法复杂度与加法复杂度分别为树子节点数量矩阵G′和失效准则参数k的线性阶。对于条件概率母函数法，在采用本文树状系统定义的条件下，其求解树状系统n中连续取k失效概率准则系统可靠度的运算复杂度与本文算法一致。但应用条件概率母函数法时，需对失效准则参数k进行讨论(分k=1和k>1两种情况)，而本文算法则实现了k取值时公式的统一，减少了算法空间复杂度。

算法适用情况方面，条件概率母函数法需要求根节点下所有子节点工作概率相同，否则算法运算复杂度趋近于各单元状态穷举。而本文算法复杂度是部件工作概率的线性阶，即不同部件的概率取值不影响算法运算复杂度。因此，本算法在求解树状系统考虑n中连续取k失效准则的系统可靠性问题上有更好的适应性。