基于熵和关联系数的概率对偶犹豫模糊多属性决策方法
2022-03-15苏冰杰卢方元
苏冰杰, 卢方元, 朱 峰
(1.厦门大学 经济学院,福建 厦门 361001; 2.郑州大学 商学院,河南 郑州 450001; 3.郑州大学 管理工程学院,河南 郑州 450001)
0 引言
犹豫模糊集[1]可以有效地包含多个不同的隶属度,目前已经被成功地应用到经济管理决策问题中,但却认为每一个隶属度发生的概率是一致的。为了有效地测量不同隶属度的概率,Zhang等[2]定义了概率犹豫模糊集。概率犹豫模糊集不仅给出了每一个隶属度发生的概率,同时解决了决策群体的意见存在不一致的情况,已经引起了国内外学者的广泛关注[3~6]。由于决策过程中存在非隶属度信息,Hao等[7]根据对偶犹豫模糊集[8]和概率犹豫模糊集提出了概率对偶犹豫模糊集,不仅给出了多种隶属度和非隶属,也考虑了二者的概率,与概率犹豫模糊集相比包含的信息更全面,更符合实际情况。
目前,概率对偶犹豫模糊集的研究引起了越来越多学者的关注。Hao等[7]首次定义了概率对偶犹豫模糊熵,但熵的公理化定义和计算公式存在缺陷。Garg等[9]定义了2种概率对偶犹豫模糊集距离测度和一系列概率对偶犹豫模糊集结算子,但是需要根据实际需求进行人为添加数据。Garg等[10]首次提出了概率对偶犹豫模糊集的关联系数,但并未考虑数据的负相关情况。考虑到概率对偶犹豫模糊元的概率存在未知的情况,Garg等[11]基于最大熵原理提出了概率确定模型,然后与概率对偶犹豫模糊麦克劳林对称平均(PDHFMSM)算子结合建立多属性决策模型。Ren等[12]提出了概率对偶犹豫模糊AHP方法,并基于VIKOR方法提出了概率对偶犹豫模糊多属性决策模型。Liu等[13]对概率对偶犹豫模糊集进行了拓展提出了区间概率对偶犹豫模糊集。
以上文献表明,概率对偶犹豫模糊多属性决策问题研究还有待完善。鉴于此,本文研究了属性值为概率对偶犹豫模糊元,属性权重完全未知的多属性决策问题。本文首先提出概率对偶犹豫模糊熵,其次考虑到目前概率对偶犹豫模糊关联系数存在的缺陷,基于熵测度和信息特征向量定义了概率对偶犹豫模糊集的关联系数。最后本文将概率对偶犹豫模糊集的熵测度和关联系数结合运用到属性权重完全未知的多属性决策问题中,并通过具体案例进行了验证分析。
1 预备知识
定义1[7]设一个非空集合为X,则在X上的一个概率对偶犹豫模糊集(PDHFS)为
A={

若X={x},则A退化为α={h(p),g(q)},一般称α为概率对偶犹豫模糊元(PDHFE),且h(p)中的元素γλ|pλ按照隶属度γλ从小到大排列,g(q)中的元素ηλ|qλ按照非隶属度ηλ从小到大排列。α的补集为αc={g(q),h(p)}。
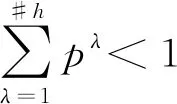
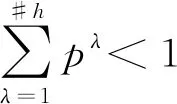
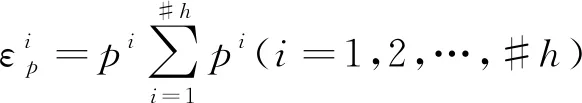
为了使隶属度集合和非隶属度集合的元素个数和概率信息保持一致,本文根据调和概率语言集[14]提出内部调和概率对偶犹豫模糊元。

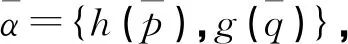
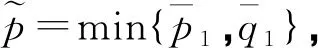
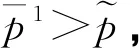

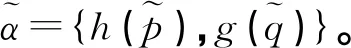
定义4[7]设任意2个概率对偶犹豫模糊元分别是α1,α2,则
(1)若score(α1)>score(α2),则α1>α2;(2)若score(α1)=score(α2),则
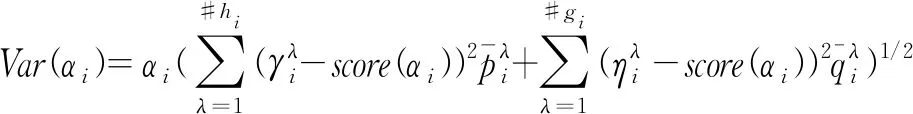

根据例1可知内部调和概率对偶犹豫模糊元中隶属度集合和非隶属度集合在元素个数和概率信息完全一致,对于后续的计算和研究更为方便。
2 概率对偶犹豫模糊元的熵和信息特征向量
2.1 概率对偶犹豫模糊熵
为了测量概率对偶犹豫模糊元的信息不确定性,本文在概率犹豫模糊熵[3]和对偶犹豫模糊熵[15]的基础上提出了概率对偶犹豫模糊熵的公理化定义和计算公式。
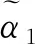
(1)0≤e(α)≤1;
(2)当e(α)=1且仅当α={{0|0},{0|0}};
(3)e(α)=0当且仅当α={{0|1},{1|1}}或α={{1|1},{0|1}};
(4)e(αc)=e(α);



(1)
其中函数f:[0,1]3→[0,1]满足:(1);f(x,y,z)=1⟺x=y=z=0:(2);f(x,y,z)=0⟺x=y=z=1:(3)f(x,y,z)在x,y,z∈[0,1]上为单调递减函数。
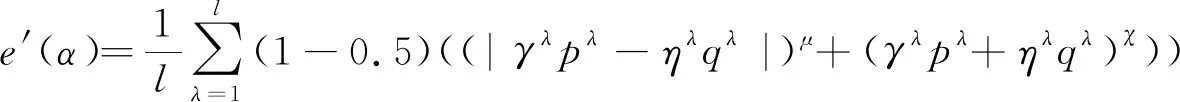
例2设2个概率对偶犹豫模糊元α1={{0.2|0.6,0.6|0.4},{0.3|0.4,0.4|0.6}}和α2={{0.2|0.3,0.6|0.2},{0.3|0.2,0.4|0.3}},分别采取和分别计算得到
e′(α1)=e′(α2)=0.7043 对于一个概率对偶犹豫模糊元,它包含的最主要的信息是值的大小与不确定性程度,这也是在具体应用中人们普遍关心的问题。本文基于文献[16]提出概率对偶犹豫模糊信息特征向量。 定义7设一个概率对偶犹豫模糊元为α={h(p),g(q)},其中h(p)={γλ|pλ|λ=1,2,…,#h}和g(q)={ηλ|qλ|λ=1,2,…,#g},则称二维向量(s(α),e(α))为的信息特征向量,记作 vec(α)=(s(α),e(α)) (2) 其中s(α)=0.5(1+score(α))代表α的大小,e(α)代表α的熵。 基于犹豫模糊关联系数[17,18]和定义7,本文定义概率对偶犹豫模糊集的关联系数。 (1)A和B的期望关联系数 (3) (2)A和B的熵关联系数 (4) (3)A和B的综合关联系数 ρt(A,B)=aρs(A,B)+(1-a)ρe(A,B)) (5) 其中a∈[0,1]。 性质1设2个概率对偶犹豫模糊集A和B,二者的综合关联系数ρt(A,B)满足 (1)-1≤ρt(A,B)≤1; (2)ρt(A,B)=ρt(B,A); (3)ρt(A,A)=1。 考虑到权重的重要性,本文提出概率对偶犹豫模糊集的加权关联系数。 (1)A和B的加权期望关联系数 (6) (2)A和B的加权熵关联系数 (7) (3)A和B的加权综合关联系数 ρwt(A,B)=aρws(A,B)+(1-a)ρwe(A,B)) (8) 其中a∈[0,1]。很容易证明ρwt(A,B)满足性质1。 设参与评价方案集Y={yi|i=1,2,…,m},属性集C={cj|j=1,2,…,n}和属性权重w={w1,w2,…,wn}T,其中属性权重完全未知。其相关决策步骤如下: 步骤2根据熵权法计算属性cj的权重为: (9) 步骤4根据公式(8)分别计算各个方案与y+和y-的加权关联系数ρwt(yi,y+)和ρwt(yi,y-),其中 (10) (11) 步骤5根据文献[18]得到方案yi(i=1,2,…,m)的贴进度CIi,其中 (12) 其中 一般CIi越大代表yi越好。 在一个智能医疗服务平台下,一名患者寻求理疗医生的治疗和帮助,在服务平台下进行挂号预约。在该网络平台下患者根据医生的声誉(c1)、收费(c2)、专业水平(c3)、治疗效果(c4)从4名理疗医生yi(i=1,2,3,4)选择一名合适自己的理疗医生进行治疗,其中收费(c2)为成本型属性,其余属性均为利益型。评价结果如表1所示。 表1 评估信息矩阵D 步骤1由于收费(c2)为成本型,为了计算方便,本文按照第4节中的步骤1对矩阵D进行处理,得到概率对偶犹豫模糊多属性决策矩阵M。 表2 概率对偶犹豫模糊多属性决策矩阵M 步骤4利用公式(10)、(11)和(12)获得每个方案的贴进度,其中参数a=0.5。 其计算结果分别是CI1=1,CI2=0.6630,CI3=0,CI4=0.2977。因此最终的排序结果为y1≻y2≻y4≻y3。即理疗医生y1最适合。 本文研究了属性权重完全未知的概率对偶犹豫模糊多属性决策问题,首先提出了概率对偶犹豫模糊集的熵,然后定义了考虑熵的概率对偶犹豫模糊关联系数,最后将二者结合建立了一种新的决策方法,并通过具体案例进行了验证分析。考虑到目前关于概率对偶犹豫模糊集的集结算子研究甚少,因此在后续的研究中重点关注其他类型的概率对偶犹豫模糊集结算子。
e(α1)=0.3733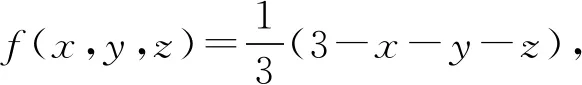
2.2 概率对偶犹豫模糊信息特征向量
3 概率对偶犹豫模糊集的关联测度
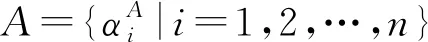

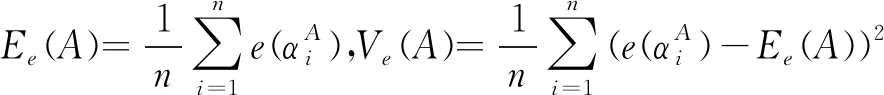
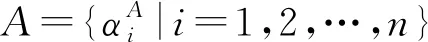
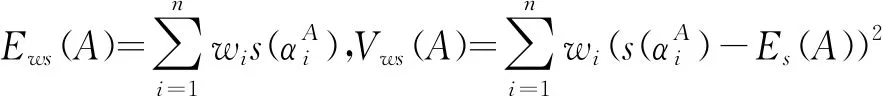
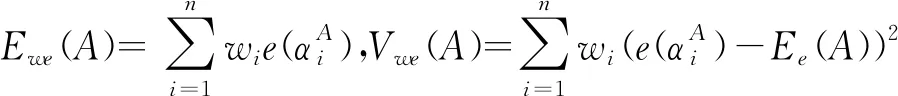
4 构建决策模型

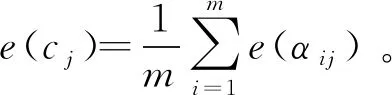
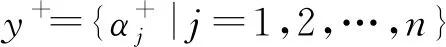
5 案例分析



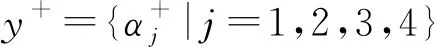
6 结论
