基于改进NAD方法的频率域声波逆时偏移
2022-03-15郎超刘少林杨晓婷徐锡伟
郎超,刘少林,杨晓婷,徐锡伟
1 北京信息科技大学理学院,北京 100192 2 应急管理部国家自然灾害防治研究院,北京 100085
0 引言
随着我国社会经济的快速发展,对石油和天然气资源的需求也与日俱增,大力提升油气勘探水平已成为当务之急,对国家资源能源储备与安全战略具有重要意义(李幼铭和刘洪,2010).叠前逆时偏移是油气勘探的有效途径之一,它以模拟地震波的传播规律为基础,并结合适当的偏移条件来获得地下介质的成像模型(底青云和王妙月,1997).偏移成像方法的研究可追溯至20世纪70年代(Claerbout,1971),受当时计算条件的限制,早期的地震偏移成像主要基于射线理论(Schneider,1978).由于射线模型只能粗略刻画实际地震波的物理属性,这类方法较难对复杂地质结构进行高分辨率成像(Liu et al.,2011).为进一步提高成像结果的质量,基于双程波方程的逆时偏移成像方法引起研究者们的关注(Baysal et al.,1983;陈生昌和周华敏,2018;Lu et al.,2020),然而求解波动方程需要消耗较多的计算资源,相应成像过程的计算效率有待提升(黄金强和李振春,2019).因此,研究高效的波动方程逆时偏移成像方法对于提高油气勘探水平至关重要(杜启振和秦童,2009).
相比于传统时间域偏移成像方法,频率域逆时偏移的优势主要体现在以下方面:(1)当时间变量经过Fourier变换至频率域时,波动方程关于频率取值相互解耦,此时具有良好的并行特性(Chen and Cao,2016);(2)不同频率取值下的地震波场可独立计算,避免了数值误差的累积与传播(Pratt et al.,1998);(3)借助复速度或者复频率,可更加方便地刻画频散或衰减效应(Song and Williamson,1995);(4)只需选取适量的频率点进行成像计算,效率较高(Sirgue and Pratt,2004).由此可见,对于频率域逆时偏移成像方法的研究尤为必要(Shin et al.,2001).
在逆时偏移成像中,绝大部分计算操作集中于模拟地下介质中地震波的传播情况(正演过程).因此,偏移效率以及成像结果的质量取决正演算法的有效性 (严红勇和刘洋,2013;Qiu et al.,2020).目前地球物理领域常用的正演数值方法包括有限差分方法(Alford et al.,1974;Moczo et al.,2007;刘少林等,2013)、有限元方法(Marfurt,1984;Liu et al.,2014;刘少林等,2014)、伪谱法(Fornberg,1975;Kosloff and Baysal,1982;黄继伟和刘洪,2020)、谱元法(Komatitsch et al.,2005;Liu et al.,2017a)等.区别于时间域波动方程的数值离散,选取频率域数值方法须在保证离散格式准确性的同时,还要兼顾到求解离散后所得大型线性代数方程组的计算代价可控(Pratt and Worthington,1990),这是大尺度区域模型频率域计算所面临的主要挑战之一(Ernst and Gander,2012).求解该线性方程组的计算代价主要依赖于其系数矩阵(也称为“阻抗矩阵”(Pratt et al.,1998))的稀疏性与条件数,这通常由离散算子的结构与性质所决定,从而频率域波动方程的数值离散应当尽可能避免复杂格式以及线性方程组的病态程度过高(Lang and Yang,2016).有限差分方法具有原理直观、格式构造简单、易于实现、方便并行等优点,有利于频率域波动方程的数值离散.这类方法已广泛应用于频率域地震波场模拟、逆时偏移成像以及全波形反演等方面(Yang et al.,2006;Xu et al.,2010;Lang et al.,2020b).然而普通差分格式在粗网格下较难对复杂地质结构(例如:强间断面、孔缝等)中地震波的传播情况进行准确模拟(Liu et al.,2017b),容易引起严重的数值频散假象(Moczo et al.,2000),进而导致偏移成像结果的分辨率受损,此时若加密离散网格,问题规模也随之增加,因此计算效率偏低.
针对普通有限差分方法所面临的难点,一些学者提出利用极小化数值速度(或者数值波数)与理论速度(或理论波数)之间相对误差的频散关系式,在不显著增加差分算子结构复杂性的前提下调整网格差分模板,可提升相应差分格式压制数值频散的能力(Zhang and Yao,2013;Jing et al.,2017;Chen and Cao,2018);另一方面,杨顶辉等(Yang et al.,2003)提出采用波场及其梯度值的线性组合来逼近高阶偏导数项,构造近似解析离散化(Nearly Analytic Discrete,NAD)方法,该方法不仅继承了普通有限差分方法格式构造的简易性,相应的离散算子还具有更强的紧致性与更高的数值精度(Yang et al.,2004);通过这两种途径所构造的新型差分方法,均可在粗网格下压制数值频散,明显提高正演模拟的计算效率.
本文根据频率域计算的特点将以上两种思路相结合,发展一种有助于大尺度区域模型频率域波场模拟与偏移成像的高效算法.具体地,在固定NAD网格差分模板的前提下通过优化模板系数得到改进NAD方法,相比于标准NAD格式,改进NAD方法可缓解离散后所形成线性方程组的病态程度(降低阻抗矩阵的条件数),频率域正演模拟效率得到进一步提升;离散后的大型稀疏线性方程组将统一采用“不精确旋转分块三角预处理子”(Inexact Rotated Block Triangular Preconditioner,IRBTP)结合Krylov子空间迭代方法进行快速求解(Lang and Ren,2015);再通过推导适当的频率域逆时偏移成像条件,并结合基于改进NAD方法的正演计算过程,分别对凹陷模型、Sigsbee2B模型以及Marmousi模型进行偏移成像;同时也将相应结果与四阶标准NAD方法以及四阶普通有限差分(Ordinary Finite Difference,OFD)方法(Jo et al.,1996)进行对比,以此来验证改进NAD方法在提高偏移效率以及成像质量方面的优势.
1 正演算法
1.1 NAD离散过程
若将常密度介质中的二维频率域声波方程记为
(1)
其中Δ表示二维Laplace算子,ω=2πf为角频率,c=c(x,z)表示波速,s为震源项,Ω表示二维计算区域.在NAD类方法的离散过程中,需要对(1)式分别关于x和z求偏导数(Yang et al.,2004),则有
(2)
为消除人工截断计算区域所产生的虚假反射波,需对Ω的边界进行处理.本文采用“完美匹配层(Perfectly Matched Layer)”吸收边界条件(Berenger,1994).应该指出的是,在频率域施加吸收边界条件来刻画波的衰减特性具有天然的便捷性,可避免因反卷积运算所产生的误差(Lang and Yang,2016).首先引入复坐标(以水平方向为例)
(3)

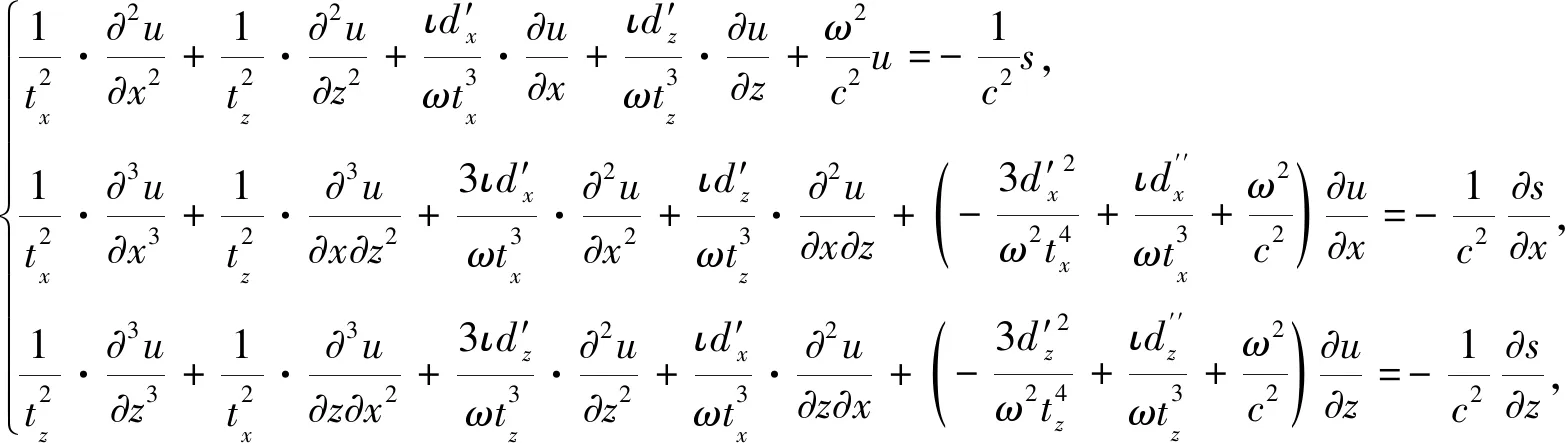
(4a)
(4b)
(4c)
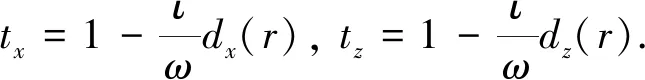
在本文的讨论中,设置x与z方向上的空间离散步长相等,统一记作h.若将(4)式中x方向上高阶偏导数在(i,j)点处进行离散的NAD网格差分模板表示为
(5)
z方向讨论类似,则(4)式中的高阶混合偏导数可借助(5)式以及方向导数的性质进行推导(Tong et al.,2011)
(6)
(7)
以及
(8)
需要指出的是,当网格模板系数取作
(9)
此时对应于四阶标准NAD方法(Yang et al.,2006).
采用所有高阶偏导数的NAD网格差分模板(5)—(8)对(4)式进行离散(具体过程可见附录A),再将二维区域Ω中的网格节点按照从上至下逐行依次排列(每行从左至右)的规则且同一节点处的波场及其梯度项相邻放置,即可形成线性方程组
Cu=b,(10)
矩阵C的稀疏分块结构如下:
(11)
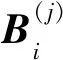
1.2 改进NAD方法
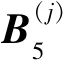
(12)
观察(12)式,阻抗矩阵的主对角元素取值仅依赖于网格差分模板系数a0与d0(忽略高阶小量)且二者均未出现在矩阵C的非主对角元素表达式中,从而可通过主对角占比目标函数
(13)
来表征阻抗矩阵的主对角元素取值集中程度,其中自变量coeff2=[a-1,a0,a1,b-1,b0,b1]T与coeff3=[c-1,c0,c1,d-1,d0,d1]T分别表示离散二阶与三阶偏导数的NAD网格模板系数所组成的向量.通过极小化(13)式可降低阻抗矩阵的条件数.若考虑理想情形,当函数dr为零时C将退化为对角矩阵从而条件数降为1,此时线性方程组的解立刻得出;另一方面,在期望函数dr减小的同时,还需保持相应数值格式离散的准确性,这里引入数值波数与理论波数的偏差来衡量差分格式压制数值频散的能力并以此作为约束条件(Zhan and Yao,2013;Jing et al.,2017).若对(5)式关于x作Fourier变换至波数域,则有波数表达式
(14)
其中(kx)num与kx分别表示x方向上数值波数与理论波数.将相位补偿θx=kxh∈(0,π)代入(14)式中,则
(15)
根据(15)式可定义波数偏差函数
(16)
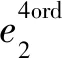
(17)
可利用MATLAB优化工具箱即可对(16)与(17)式进行有效求解,所得最优网格模板系数为
(18)
将(18)式代入(5)—(8)式,即可得改进NAD网格差分模板.事实上,上述改进思想不仅适用于四阶NAD方法,对任意阶标准NAD格式(例如:六阶、八阶)均可在其基础上进行来提升频率域正演模拟的效率.
对于线性方程组(10)的求解下文均采用不精确旋转分块下三角(IRBLT)预处理子加速GMRES方法进行,关于该预处理迭代方法的具体实施步骤以及理论分析结果可参见(Lang et al.,2020a).
1.3 改进NAD方法的正演效率评估
本节通过对均匀介质模型进行波场模拟来考查改进NAD(简记为NAD*)方法的正演计算效率并与四阶标准NAD(记作NAD4)方法进行对比.所考虑二维计算区域规模为5 km×5 km,网格参数201×201,背景速度c=3.5 km·s-1.
在下文所有数值试验中,(1)式中的震源右端项均取作Ricker子波,其频率表达式为(Lang et al.,2020b)
(19)
其中A为振幅,f0表示震源主频.对该震源子波的频谱分析结果显示其大部分能量集中于0~2.5f0频段内,因此可采用这一频段的单频波波场通过离散Fourier逆变换(IDFT)合成时间域波场来观察数值频散效应.为量化离散网格的疏密程度,需定义“网格频率”(记作Gf)为最短步长所包含的网格点数(Liu,1997)
(20)
其中λmin表示最短波长,cmin为最小波速.若设置A=1,f0=20 Hz,则Gf=2.8为NAD4方法压制数值频散时网格疏密度的临界值(Lang and Yang,2016).与此同时,还将数值格式的频散误差定义为不同波的传播角度β下数值速度关于理论波速的最大相对值(Jing et al.,2017)
(21)
对于给定的数值离散格式,该频散误差随网格频率Gf增长而增加,这意味着离散网格越粗则频散误差越大,反之亦然.经过反复测试,当NAD4方法的网格频率Gf(NAD4)=2.8以及NAD*方法的网格频率Gf(NAD*)=2.92时,这两种方法的频散误差相等
ε(NAD*)=ε(NAD4)=0.0258,(22)
此时在频率取值分别为15,25,35,45 Hz下两种方法所对应的阻抗矩阵条件数如表1所列.表中显示各种情形下由NAD*方法离散所生成阻抗矩阵的条件数均小于NAD4方法;当f=8,35 Hz时由NAD*方法计算得到的单频波波场快照如图1所示;利用震源能量集中频段(1~50 Hz)的单频波波场快照分别合成对应于NAD*与NAD4方法无明显数值频散的时间域波场快照,如图2所示.此时NAD4方法所需计算时间为3.19 min,相比之下,NAD*方法只需2.93 min,可节省约8.15%.
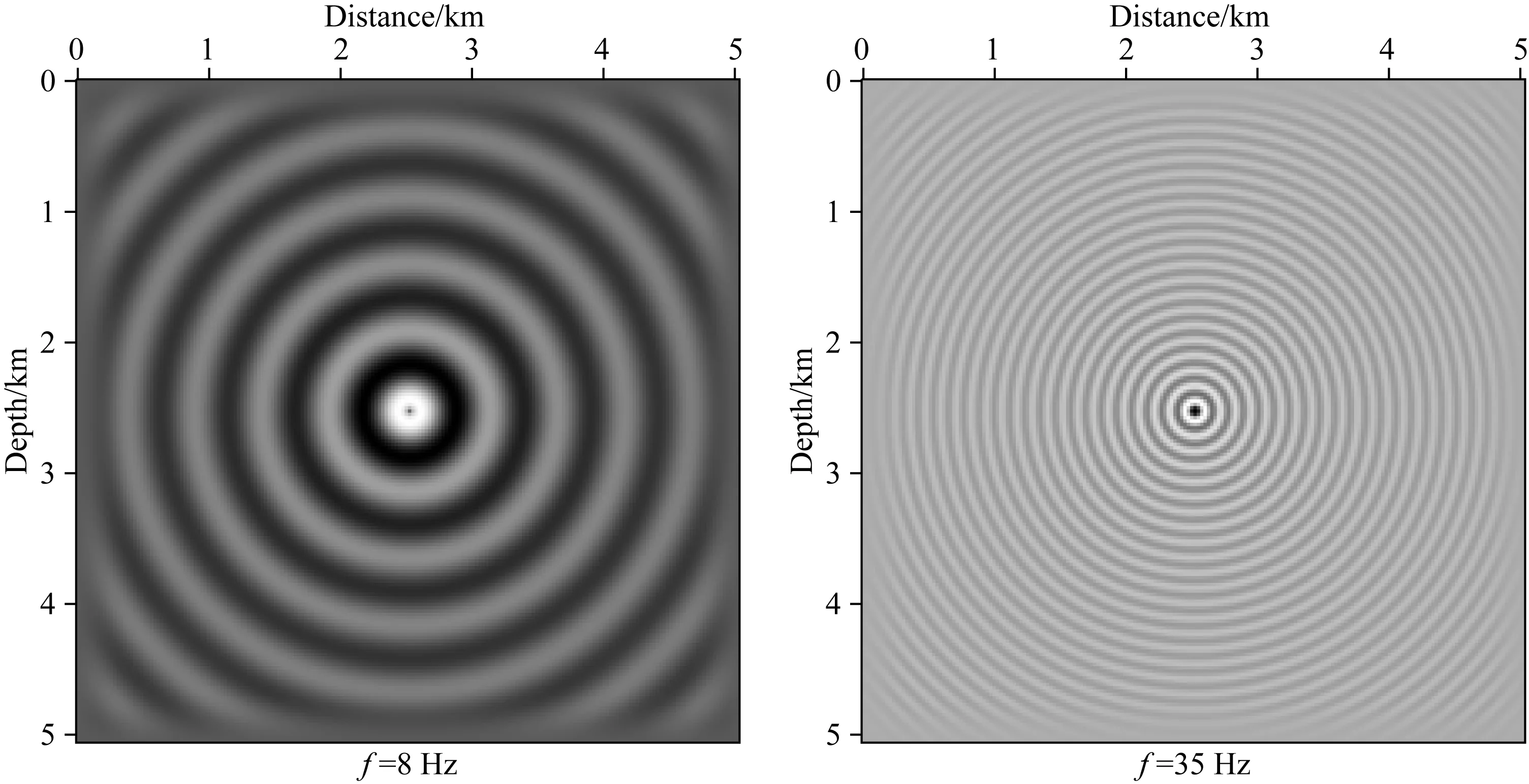
图1 均匀介质中由NAD*方法计算得到的单频波波场快照Fig.1 Mono-frequency wave-field snapshots by NAD* method in homogeneous medium

图2 均匀介质中由两种方法得到在t=0.5 s时刻的时间域波场快照Fig.2 Time-domain wave-field snapshots at t=0.5 s point by two methods in homogeneous medium
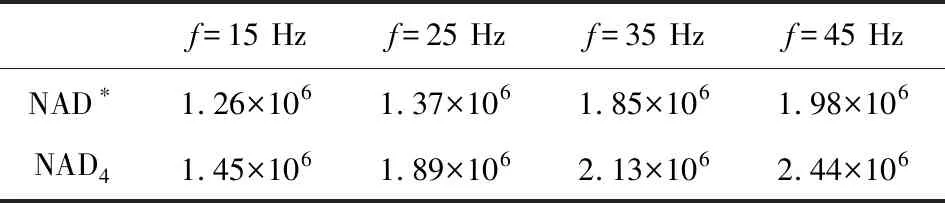
表1 不同频率取值下两种方法离散所得阻抗矩阵的条件数Table 1 Condition number of impedance matrix by two methods for various values of frequency
2 频率域逆时偏移成像原理
经典的时间域逆时偏移互相关成像条件为(Claerbout,1971;Whitmore and Lines,1986)
(23)
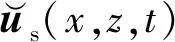
=us(x,z,ω)·ur(x,z,ω),(24)
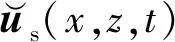
I(x,z)=F-1[us(x,z,ω)·ur(x,z,ω)]
(25)
为消除不同位置处震源强度对成像结果的影响,需要将(25)式进行归一化(也称为照明补偿(Zhou et al.,2018)).根据Parseval等式,归一化因子在时间域与频率域保持能量不变性,即
(26)
则带有照明补偿的频率域逆时偏移成像条件为
(27)
其中σ为取值很小的正数,引入该参数可避免(27)式分母为0.下文讨论均采用带有照明补偿的互相关偏移成像条件.实际计算中,成像结果可通过选取(27)式的被积函数在所考虑频段范围0~ωmax中的不同频率组分进行叠加而获得.
在采用互相关逆时偏移条件对复杂地质结构进行成像时,由于首波、潜水波以及绕射波的存在,偏移过程将会产生严重的低频噪声,导致成像结果的分辨率受损(Qiu et al.,2020).为抑制低频噪声,通常可采用Laplace滤波对波场关于传播角度进行衰减(Zhang and Sun,2009).具体地,若将离散Laplace算子记为

(28)
则滤波后成像结果的矩阵形式为
IL(x,z)=L·I(x,z)+I(x,z)·L.
(29)
由(29)式可见,Laplace滤波操作简单,所需计算量很少.
3 频率域逆时偏移算例
为检验NAD*方法频率域逆时偏移的数值效果,本节运用该方法分别对凹陷模型和Sigsbee2B模型进行偏移成像并将相应结果与NAD4方法和四阶普通有限差分(简记为OFD)方法进行对比.此外,我们还运用NAD*方法对Marmousi模型的标准数据进行计算.以下偏移计算中,接收器位于计算区域顶部与PML分界面处并且逐个节点密集放置,震源在接收器下一层并根据模型的复杂程度进行选取,PML区域厚度为δ=10 h,对于各种模型其他计算参数的取值情况见表2.

表2 对各种介质模型进行频率域逆时偏移的基本参数表Table 2 Parameter table of frequency-domain reverse time migration for various media models
3.1 凹陷模型
首先考虑凹陷模型(如图3所示),其上半区域背景速度取值为2.5 km·s-1,下半区域为3.0 km·s-1.由于模型相对简单,在偏移成像中每隔25个节点设有1个震源并且沿水平方向中心对称放置,共计7个震源.在表2所列的基本参数设置下,网格频率Gf=2.8.
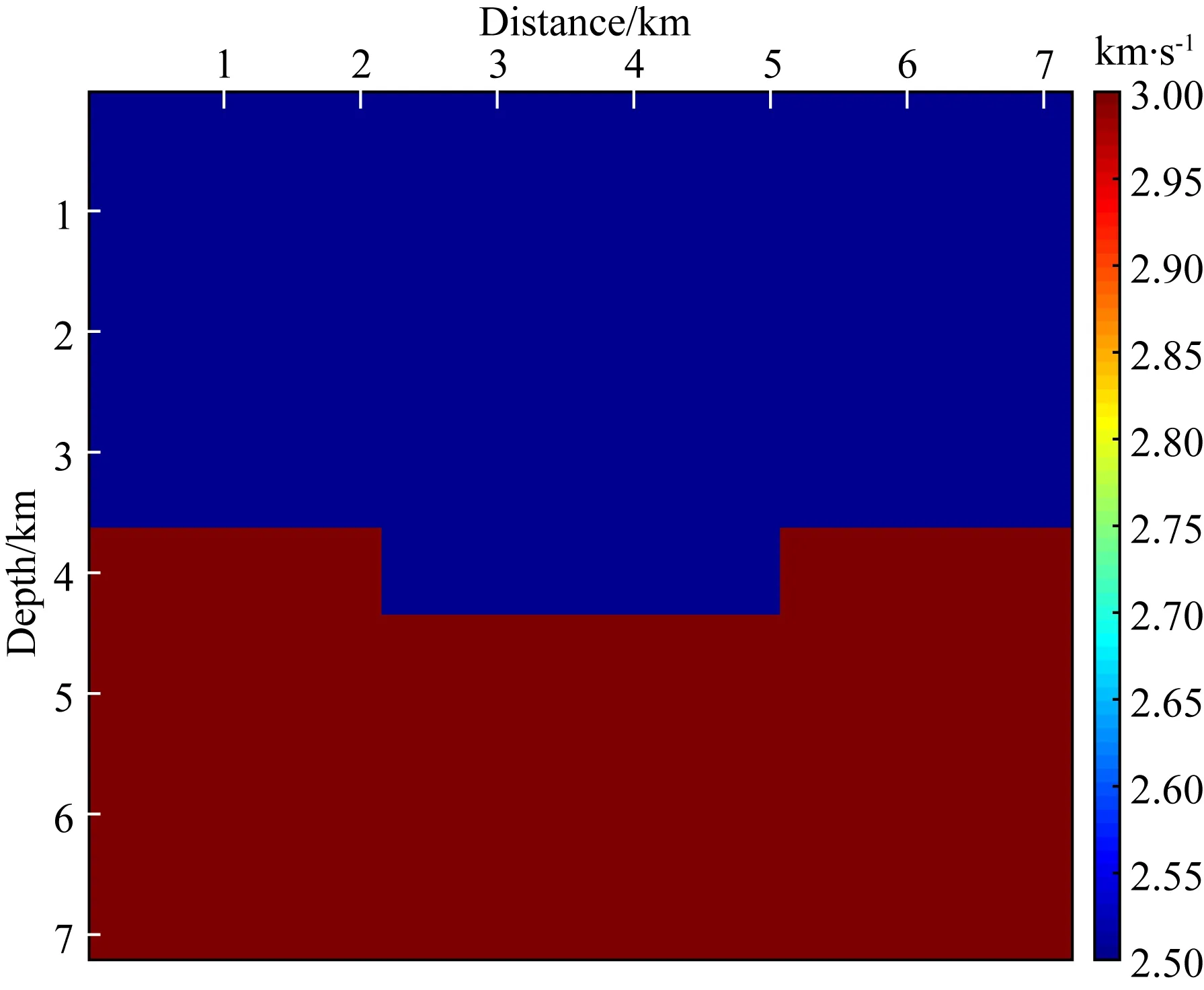
图3 凹陷模型Fig.3 Sunken model
本小节分别采用NAD*、NAD4与OFD方法进行偏移计算,所得成像结果如图4所示.从图中可见两种NAD方法的图像界面清晰,分辨率较高;而OFD方法的成像结果中在界面上方存在明显的数值频散并且区域底部出现少许假象,这是由于此时离散网格对于OFD方法而言过于粗糙而导致波场计算的精度偏低,正演模拟的数值误差体现在最终偏移成像结果中.
根据以上分析,可通过加密离散网格消除图4中OFD方法成像结果的数值频散.经过测试,当步长减少至27.0 m时频散开始消失,此时的网格规模为259×259,相应成像结果如图5所示.我们统计三种方法在得到准确偏移结果时所需的最少计算时间(如表3所列),发现NAD*方法用时最少,相比于NAD4与OFD方法,大致分别节省10.05%和19.18%.
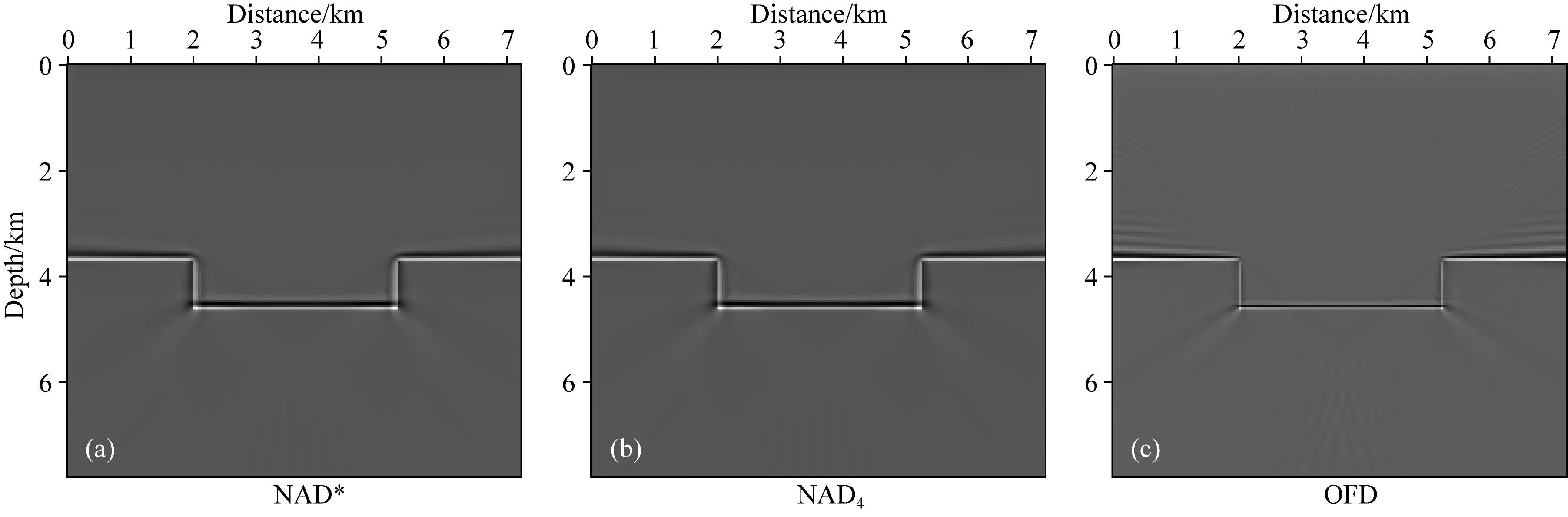
图4 凹陷模型偏移成像结果(a)改进NAD方法;(b)四阶NAD方法;(c)四阶OFD方法.Fig.4 Migration imaging results of sunken model(a)Improved NAD method;(b)4th-order NAD method;(c)4th-order OFD method.
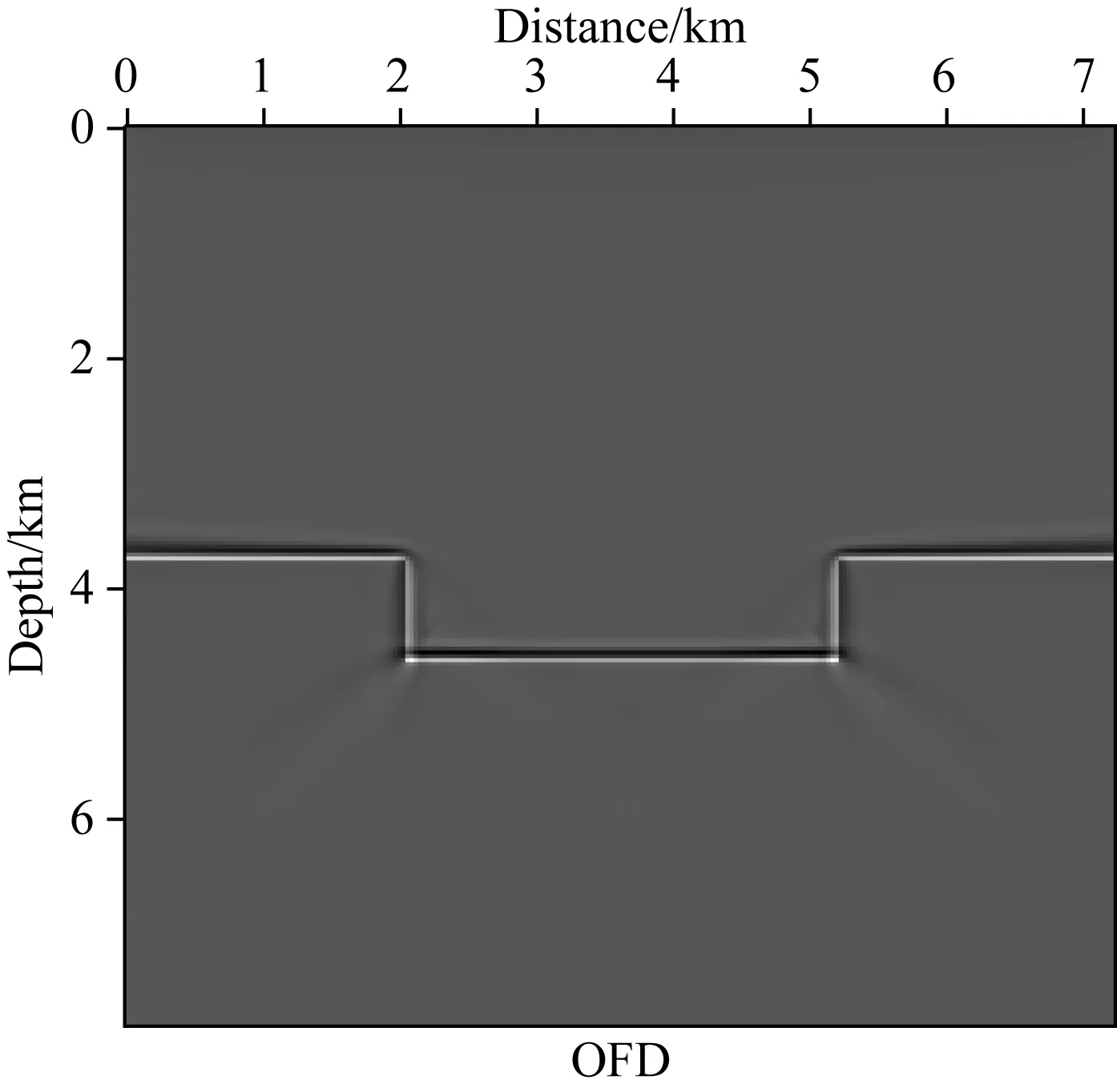
图5 细网格(h=27.0 m)下由OFD方法计算凹陷模型的偏移成像结果Fig.5 Migration imaging results of sunken model on fine grid (h=27.0 m)by OFD method
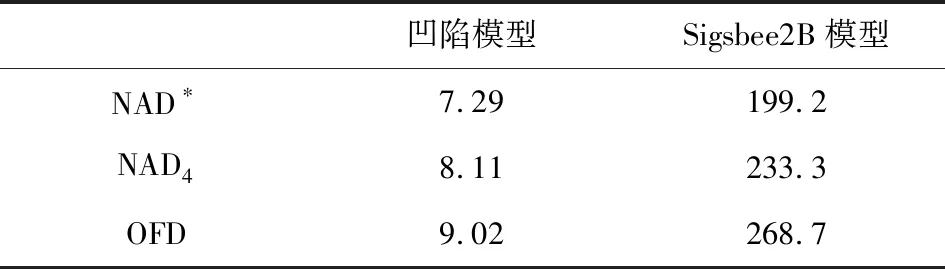
表3 不同方法计算准确偏移结果所需最少计算时间(单位:min)Table 3 Least time of computing accurate migration imaging for various methods (unit:min)
3.2 Sigsbee2B模型
Sigsbee2B模型是偏移方法基准测试的国际通用模型(Paffenholz et al.,2002),接下来对其进行成像计算.首先将原始模型进行重采样(现规模为801×301)并将速度值换算至国际标准单位(km·s-1).如图6所示,计算区域中部出现一个高速异常的盐丘体,对盐丘底部层进行准确成像是该模型成像的难点.为此,本次试验放置更多震源,间隔10个节点,共计79个.
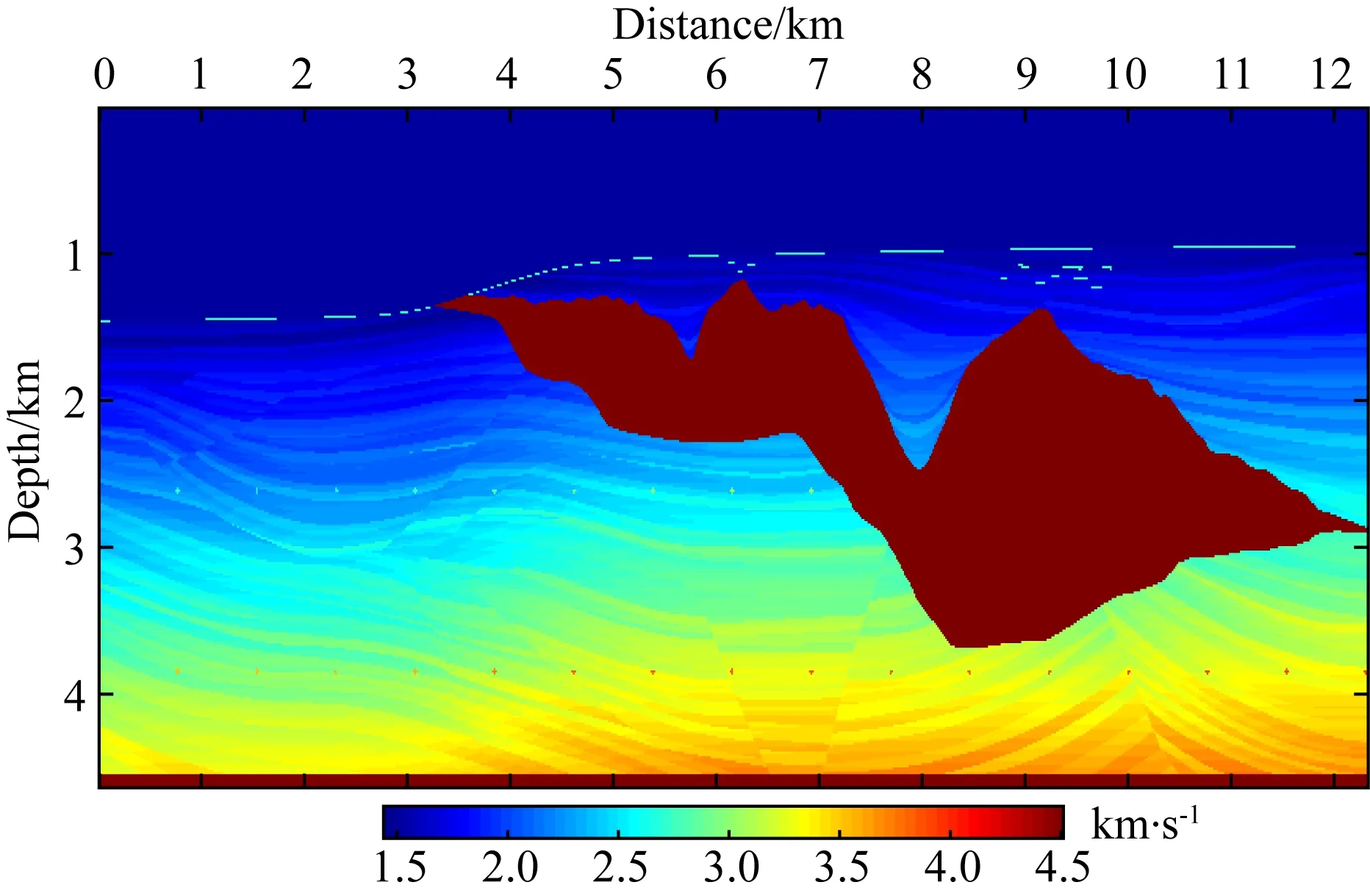
图6 Sigsbee2B模型速度结构Fig.6 Velocity of Sigsbee2B model
图7中分别显示了由NAD*、NAD4以及OFD方法计算的偏移成像结果,可以看到由NAD类方法所得到的结果相对清晰,并对盐丘底部区域进行了准确刻画,而OFD方法的图像中在盐丘顶部与底部(例如:箭头所指处)均出现虚假的层状结构,此为数值频散,需加密离散网格来消除这些假象.经过试验,当网格步长降至12.2 m时频散开始消失,相应偏移结果可见图8.此时三种方法得到准确结果所需最少计算时间如表3所列,同样NAD*方法用时最少,相比于NAD4与OFD方法可分别加速14.63%和25.86%.

图7 Sigsbee2B模型偏移成像结果(a)NAD*方法;(b)NAD4方法;(c)OFD方法.Fig.7 Migration imaging results of Sigsbee2B model(a)NAD* method;(b)NAD4 method;(c)OFD method.

图8 细网格(h=12.2 m)下由四阶OFD方法计算的Sigsbee2B模型偏移成像结果Fig.8 Migration imaging results of Sigsbee2B model on fine grids (h=12.2 m)computed by 4th-order OFD method
3.3 Marmousi模型
最后运用NAD*方法对Marmousi模型(Versteeg,1994)(如图9所示)进行偏移成像,本小节采用标准数据进行计算(某单炮记录如图10所示),其他参数设置见表2.由NAD*方法计算得到的偏移成像结果如图11所示,尽管区域顶部受噪声干扰明显,但模型的分层界面基本显现,并且未见数值频散,这也进一步检验了文中所述频率域偏移成像方法的正确性.
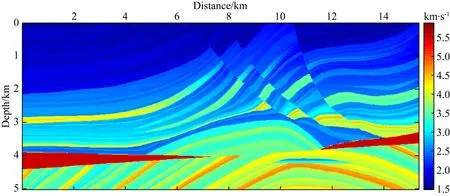
图9 Marmousi速度模型Fig.9 Marmousi velocity model

图10 标准数据的某单炮记录Fig.10 Single-shot record of standard data

图11 由NAD*方法计算得到Marmousi模型偏移成像结果Fig.11 Migration imaging results of Marmousi model computed by NAD* method
4 结论
逆时偏移成像的关键在于正演过程中如何快速有效地求解波动方程,作为一种高精度数值离散方法,NAD方法尤其适用于频率域正演模拟与偏移成像计算.本文通过优化NAD格式的网格差分模板系数,构造改进NAD方法.相比于标准NAD差分格式,改进NAD在数值离散精度不受损失的前提下降低了离散后所得阻抗矩阵的条件数,从而节省相应线性方程组求解所需的计算代价并使得迭代求解过程更加稳定.因此,采用改进NAD方法进行正演模拟可提高频率域计算效率,有助于增进大尺度区域频率域波场模拟与成像的实用性.随后,本文将改进NAD方法与频率域逆时偏移原理相结合,分别对凹陷模型、Sigsbee2B模型以及Marmousi模型实施偏移成像,并与标准四阶NAD方法和四阶OFD方法进行对比.数值结果显示了改进NAD方法在压制数值频散与提高偏移成像效率方面的显著优势;特别是对于Sigsbee2B模型的偏移试验,当得到准确成像结果时改进NAD方法相比于四阶NAD与OFD方法可分别节省约14.63%和25.86%的计算时间;Marmousi模型的可靠偏移成像结果进一步表明改进NAD方法对于复杂介质模型成像的有效性.
附录A 阻抗矩阵的稀疏结构推导
当采用NAD网格差分模板(5)—(8)式离散频率域声波方程时,(4a)式可离散为
(A1)
(4b)式离散为
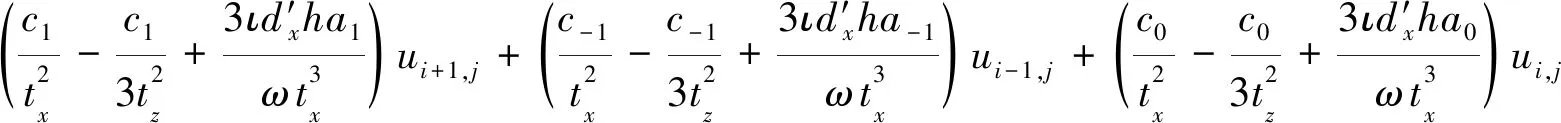
(A2)
(4c)式离散为
(A3)
若将二维区域Ω中的网格节点按照逐行次序排列(每行从左至右),则有网格节点序号对应关系k=nx·(j-1)+i,并且同一节点处的波场及其梯度项如下放置
(A4)
可形成阻抗矩阵的稀疏分块结构(11)式.
附录B 阻抗矩阵的非零子块具体元素表达式
(B1)
(B2)
(B3)
(B4)
(B5)
(B6)
(B7)
(B8)
(B9)
其中j为分块行号,跟随区域内节点的位置而变化,上述表达式中变量dx,dz,tx,tz的取值依赖于该指标.
