基于BTTB矩阵的快速高精度三维磁场正演
2022-03-15袁洋崔益安陈波赵广东柳建新郭荣文
袁洋,崔益安,陈波*,赵广东,柳建新,郭荣文
1 中南大学地球科学与信息物理学院,长沙 410083 2 有色资源与地质灾害探查湖南省重点实验室,长沙 410083 3 中南大学有色金属成矿预测与地质环境监测教育部重点实验室,长沙 410083
0 引言
磁法勘探是一种最为常见的地球物理勘探方法,其主要利用地下岩石和矿物的磁性差异所引起的磁异常来区分目标异常体(柳建新等,2016),已被广泛应用于矿产资源勘探(Hinze et al.,2013;周文月等,2021)、考古(Cella and Fedi,2015;Fedi and Florio,2003)、军事地球物理(Hiergeist et al.,2015)、区域大地构造和板块碰撞演化(Gao et al.,2013;Hemant and Mitchell,2009;Rajaram and Langel,1992;罗凡等,2021)等方面.随着高精度卫星磁测和航空磁测的普及,磁法勘探将会在越来越多的领域中发挥重要作用.通过三维磁化率成像反演,高精度和高分辨率的磁测数据能反映地下三维磁化率分布,并获得丰富的地质构造信息.但当处理大规模磁异常数据时,磁异常三维反演算法存在计算效率较低和内存占用巨大等问题,严重制约着其在磁法勘探的实际应用.
正演是反演的基础,正演算法的计算效率和计算精度直接影响着反演的耗时和可信度.磁场正演计算方法可分为空间域方法(Vacquier et al.,1951;Hughson,1964;Bhattacharyya,1964;Sharma,1966;Hjelt,1972;Plouff,1976;Kunaratnam,1981;Blakely,1996;Ren et al.,2017a,b;郭志宏等,2004;骆遥和姚长利,2007)和频率域方法(Bhattacharyya,1966;Tontini,2005;Tontini et al.,2009;吴宣志,1981;柴玉璞和万海珍,2020).空间域算法通常采用解析公式单独计算各个单元体的异常值,再进行累加求和.这类算法具有计算精度高的优点,但其计算效率较低,特别是当模型复杂需要精细剖分时,计算时间会显著增加.
频率域方法由于引入了快速傅里叶变换(FFT),计算效率较高,但受限于FFT算法固有的缺陷,例如混叠效应、边界效应和强制周期化等(Bracewell,1978;Percival and Walden,1993;Boyd,2001;Wu and Tian,2014),导致这类算法正演精度较低.近年来,频率域算法也不断得到改进和运用.例如,Wu和Tian(2014)提出高斯-快速傅立叶变换(Gauss-FFT)算法,在每一个积分区间采用高精度高斯型数值积分代替传统FFT算法中的梯形法则,大大提高了正演计算精度,被广泛用于频率域三维重磁场正演(Zhao et al.,2018;曾明等,2019)、莫霍面反演(Zhao et al.,2020)和地形校正(Wu,2016;Wu and Chen,2016)等.类似地,基于FFT的空间波数域混合方法(李昆等,2019;周印明等,2020)同样显著提升了正演的计算效率.虽然这些频率域方法在较高计算效率的情况下实现了较高的计算精度,但是与空间域解析解之间的误差还是不可忽略.
鉴于上述存在的问题,如何使正演算法同时具备空间域的高精度和频率域的高效率成为新的研究热点.在三维重磁正反演解释中,直立长方体是最常用的一种场源几何剖分单元.当场源区域和观测面都采用规则且均匀的剖分时,位场数据处理或正演的雅克比矩阵(即核矩阵)具有平移等效性和互换等效性(姚长利等,2003),其实质是一类特殊的分块Toeplitz矩阵,即块-托普利兹-托普利兹-块(Block-Toeplitz Toeplitz-Block,BTTB)矩阵(陈龙伟,2013;Zhang and Wong,2015;Zhang et al.,2016;Wu,2018;Chen and Liu,2019;Hogue et al.,2020).陈龙伟(2013)发展了基于BTTB矩阵的Block Circulant Extension(BCE)算法,采用FFT快速实现该类矩阵和向量的卷积计算(Vogel,2002),并用于磁场数据的向上和向下延拓,显著提升了空间域数据处理的计算效率.Chen和Liu(2019)采用存储中间变量的策略,进一步优化了BCE算法,显著提升了重力异常正演的计算效率.Qiang等(2019)将BCE算法和分层插值法结合,分别正演了水平观测面和起伏地形上的磁异常.Hogue等(2020)将BCE算法进行扩展,使其适用于磁异常正演所产生的非对称的普通BTTB矩阵.
为了进一步降低磁场正反演中核矩阵的内存占用并提高计算效率,本文借鉴Chen和Liu(2019)重力场正演的优化方法,改进了空间域磁异常ΔT及其梯度的正演算法,使其更为高效.首先采用无解析奇点的长方体ΔT场及其梯度场公式保证计算精度,利用BTTB矩阵的等效性压缩核矩阵大大降低内存需求,并且在计算核矩阵时引入中间变量减少重复计算;然后采用Vogel(2002)中基于BTTB矩阵和FFT的快速算法进一步提高计算效率;再分别进行垂直磁化和倾斜磁化两种情况下的正演数值模拟,验证算法的效率和精度;最后将快速算法运用到磁场反演中,并用合成模型实验验证算法的实用性.
1 理论和方法
1.1 基于直立长方体的磁场正演公式
本研究的场源区域和观测面的剖分如图1所示,坐标原点位于场源区域的上界面,z轴向下.将地下场源区域沿x、y、z方向剖分成Nx×Ny×Nz个长方体单元,三个方向间隔分别为Δx、Δy、Δz.(ξa,ηb,ζc)为长方体单元(a,b,c)的中心坐标.假设每个长方体单元的磁化率为常数,κ(ξa,ηb,ζc)为该单元体对应的磁化率,其中a=1,2,…,Nx,b=1,2,…,Ny,c=1,2,…,Nz.观测点分布于高度为z0平面上的Nx×Ny个规则网格节点上.
单个长方体在任意观测点P(x,y,z)产生的ΔT场及其梯度场的无奇点解析表达式为(骆遥和姚长利,2007):
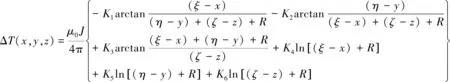
(1)
(2)
(3)
(4)
值得注意的是,公式(1)计算的ΔT为磁异常总强度矢量Ta在T0方向上的投影.对于一般情况(即当磁异常强度不大时),实测的ΔT(即磁场总强度T与T0的模量差)可近似为式(1)正演计算的ΔT,通常具有足够精度.但当存在强磁性体或磁异常幅值大时,实测ΔT和正演ΔT之间的误差不可忽略(袁晓雨等,2015).一些学者提出了实测ΔT的处理和正反演的方法(Zhen et al.,2019;Sun et al.,2019;甄慧翔等,2019;孙石达等,2020;胡正旺等,2021),有效改善了两者之间的误差.本文针对一般情况,根据线性叠加原理,地下场源在观测点(xi,yj,z0)产生的ΔT场及其梯度场可以表示为所有长方体单元磁场响应累加求和的形式:
·G(xi,yj,z0;ξa,ηb,ζc),
(5)
·Gx(xi,yj,z0;ξa,ηb,ζc),
(6)
·Gy(xi,yj,z0;ξa,ηb,ζc),
(7)
·Gz(xi,yj,z0;ξa,ηb,ζc),
(8)
式中,i=1,2,…,Nx,j=1,2,…,Ny,G、Gx、Gy、Gz分别为ΔT场及其梯度场的核函数:
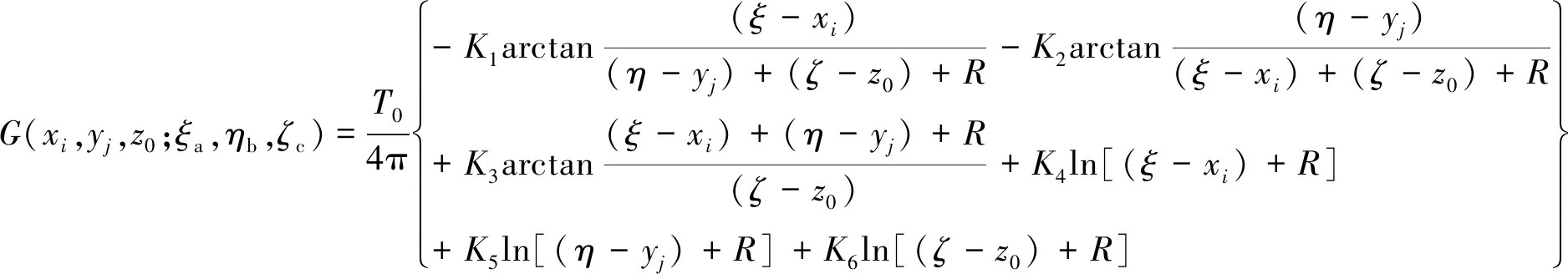
(9)
(10)
(11)
(12)
公式(5)—(8)可以采用矩阵形式表示为(沿场源区域的垂直方向先逐层计算再进行累加求和):
(13)
(14)
(15)
(16)
1.2 快速正演
基于上述剖分,当观测点与长方体单元中心点在水平面上的投影重合时,对于任意的Nx、Ny、Δx、Δy,上述核矩阵都是一类特殊的矩阵,称为BTTB矩阵,即分块Toeplitz矩阵.这类矩阵具有大量重复的矩阵元素,因此仅需计算部分元素即可得到全部矩阵,从而可以减少正演过程中计算核矩阵的耗时.例如,当场源为倾斜磁化时,ΔT及其梯度的核矩阵为普通的BTTB矩阵,在正演时仅需计算(2Nx-1)×(2Ny-1)个核矩阵元素就能得到完整的核矩阵.
特别是垂直磁化时,组成Gc、Gzc、Gyc的对称Toeplitz矩阵是对称分布的,但Gyc中对称的两个Toeplitz矩阵的元素互为相反数.另外,组成Gxc的Toeplitz矩阵块也是对称分布的,矩阵块中沿主对角线对称的元素互为相反数.对于这些特殊的BTTB矩阵,只需要计算核矩阵的第一行或者第一列(即Nx×Ny个核矩阵元素)就能构建完整的核矩阵,当计算第一层长方体单元对所有观测点产生的磁异常时,只需第一层第一个单元体(ξ1,η1,ζ1)对所有观测点(xi,yj,z0)所产生的Nx×Ny个核矩阵元素,i=1,2,…,Nx,j=1,2,…,Ny,即令:

(17)
(18)
(19)
(20)
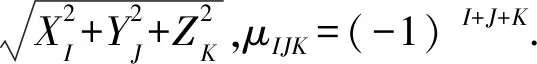
对于垂直磁化(I0=I=90°、A0=A=0°),此时l=m=L=M=0、n=N=1,于是K1=K2=K4=K5=K6=0、K3=2,公式(17)—(20)可简化成:
(21)
(22)
(23)
(24)
通过预先计算并存储部分中间变量可以进一步优化计算核矩阵的效率,引入的中间变量为:
(25)
(26)
(27)
(28)
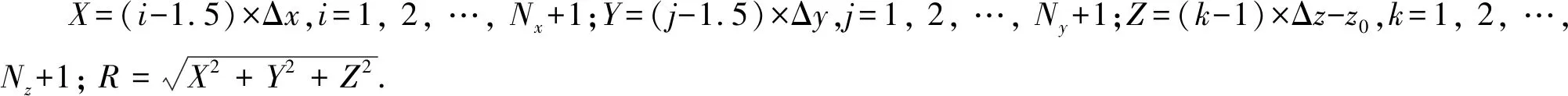
计算一个长方体单元对一个观测点的磁异常时,只需要取长方体单元的8个角点所对应的8个中间变量进行累加求和.当逐层计算每一层的Nx×Ny个核矩阵元素时,如果不预先计算并存储中间变量,相当于Nz层总共计算8×Nx×Ny×Nz次中间变量.反之,则只需要计算(Nx+1)×(Ny+1)×(Nz+1)次中间变量,计算量减少至约之前的1/8.
当Δx=Δy时,能利用对称性提升计算ΔT和ΔTz的核矩阵的效率.以计算ΔT为例(对ΔTz同样成立),一个长方体单元对所有观测点所产生的Nx×Ny个核矩阵元素具有对称性,如图2所示(箭头位置对应的核矩阵元素相同),用公式表示为:
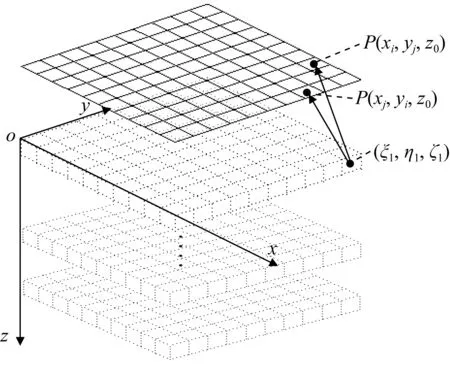
图2 一个长方体单元对所有观测点的磁异常ΔT核矩阵的对称性示意图Fig.2 The schematic diagram of the symmetry of the kernel matrix generated by a cuboid unit for the magnetic anomaly ΔT
G(xi,yj,z0;ξ1,η1,ζ1)=G(xj,yi,z0;ξ1,η1,ζ1).
(29)
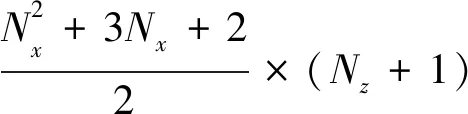
事实上,正演计算并不需要一次性计算并存储整个Nz+1个界面的中间变量,而是在逐层计算每一层核矩阵元素时,仅预先计算并存储这一层的中间变量,对应长方体单元上下两个界面的角点.这样增加的内存与三维磁化率向量相比数量级较小,可忽略不计.图3直观地展示了中间变量的功能,每个长方体单元在其上、下界面各有4个角点,而且上下两个长方体单元会共用4个角点,例如长方体单元(ξ1,η1,ζ1)与(ξ1,η1,ζ2)共用4个角点(白色圆点表示).为了说明中间变量的互换性,以长方体单元(ξ1,η1,ζ1)的上界面4个角点(三角形表示)为例,当观测点位于对角线上的网格时,关于对角线对称的角点对应的t值相同,即实线对应的t值相同(实线,虚线和点划线分别对应3个不同的t值).
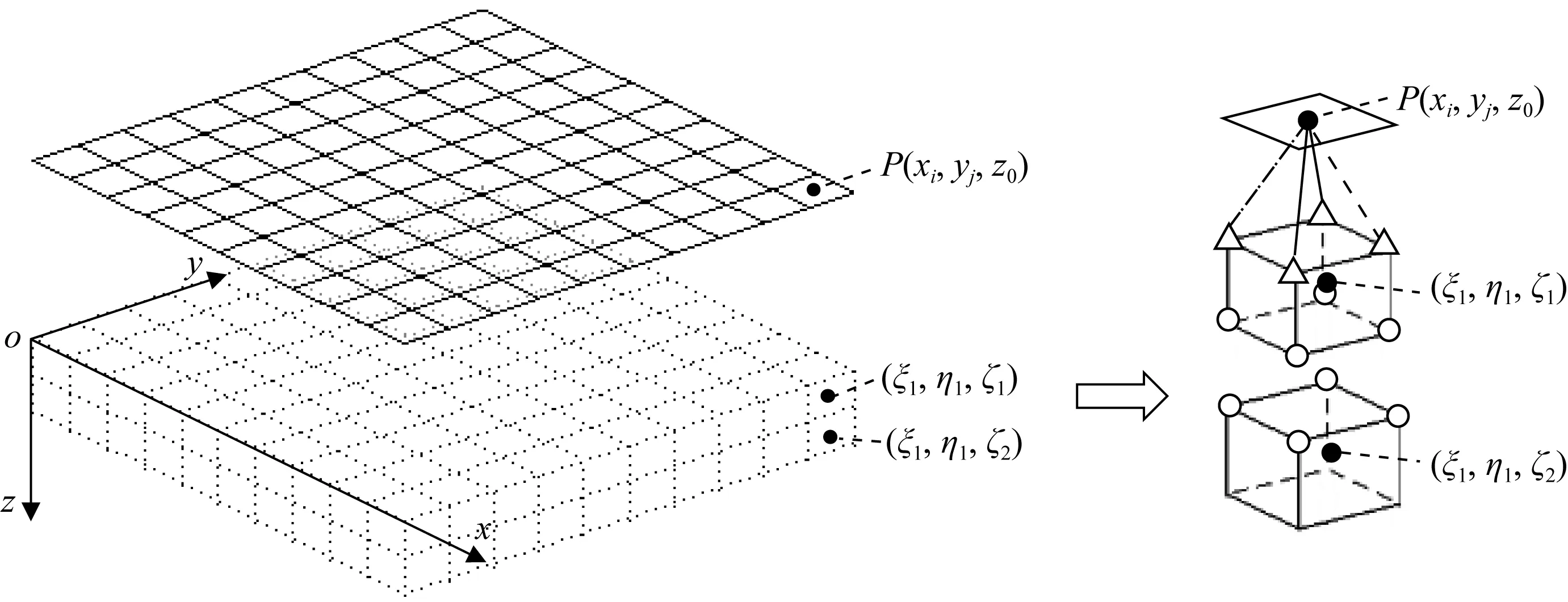
图3 中间变量t值等效示意图Fig.3 The schematic diagram of the equivalence of t values
表1对比了当Δx=Δy,Nx=Ny时,快速正演算法分别在垂直磁化和倾斜磁化下计算ΔT场及其梯度场所需存储的矩阵元素个数,据此可估算出计算量和内存随剖分个数的变化关系.

表1 Δx=Δy,Nx=Ny时快速正演计算方法所需存储的矩阵元素个数对比Table 1 Comparison of the number of matrix elements of storage required in the proposed method,when Δx=Δy and Nx=Ny
利用上述过程构建磁异常ΔT及其梯度的正演核矩阵后,可以利用基于BTTB矩阵和FFT的快速算法(Vogel,2002)计算该层核矩阵与其对应的磁化率向量的乘积,进一步提高正演计算效率,BTTB矩阵和向量乘积的快速算法的详细过程见附录A.
图4为快速正演算法流程图,其中虚线路线提升的计算效率最高,点划线最低.
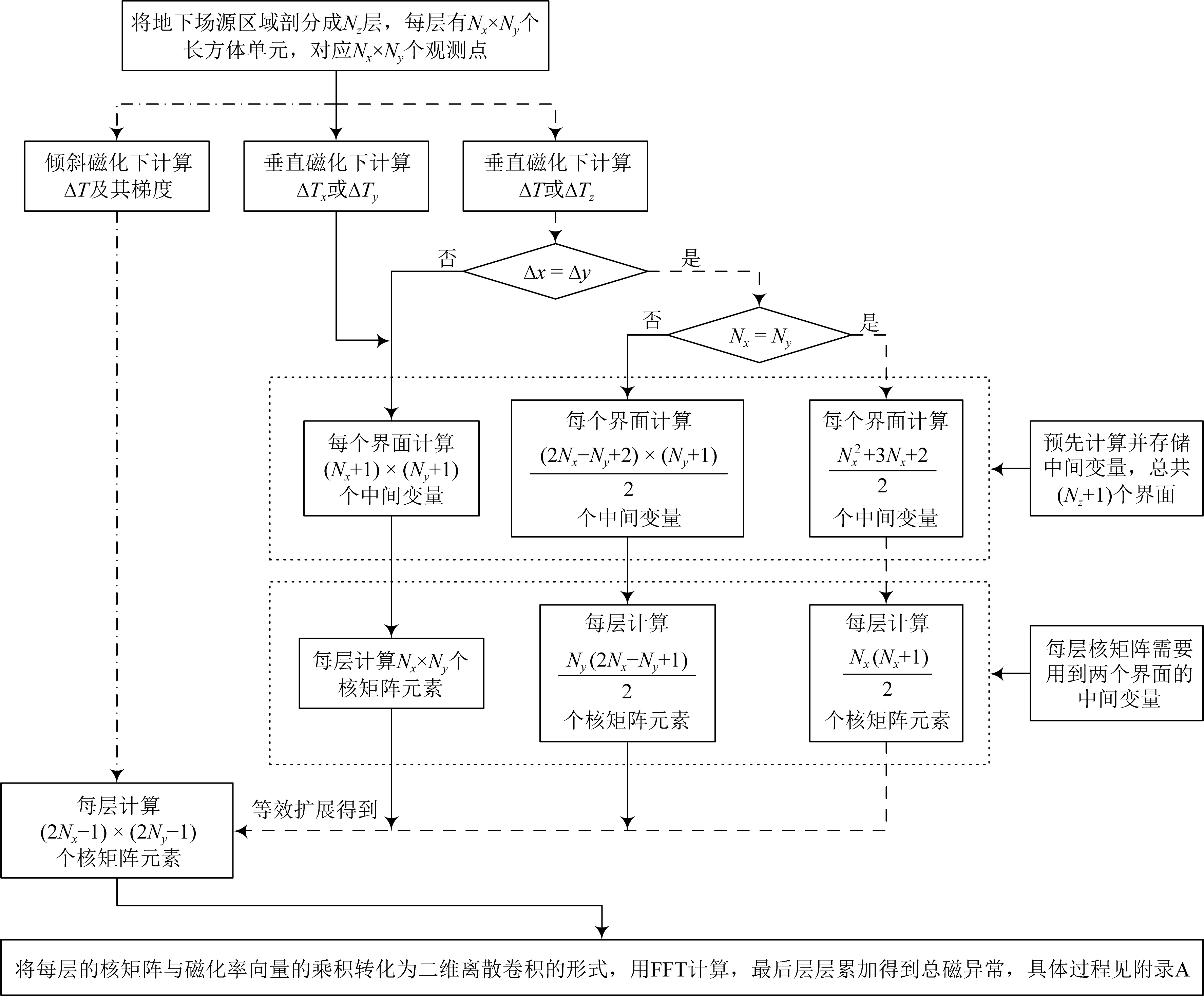
图4 快速正演算法流程图Fig.4 The flow chart of the fast forward method
2 数值模拟
为了验证快速算法的准确性和高效性,本节将从计算效率,计算精度和内存需求这三个方面对传统空间域解析解(Blakely,1996),最新频率域Gauss-FFT算法(Wu and Tian,2014)和改进的快速算法进行对比.由于使用的高斯点个数不同,Gauss-FFT算法的计算效率和计算精度也不同,为了更合理的对比计算效率,本文将选用4点和8点的Gauss-FFT算法.另外,从1.2节可知,相比于倾斜磁化,垂直磁化时形成的BTTB矩阵具有更多重复的元素,所用的快速算法计算效率更高,因此本节会分开进行讨论.
2.1 垂直磁化模型
本文以计算球异常体在水平观测面产生的磁异常ΔT及其x方向梯度ΔTx为例进行说明.采用垂直磁化,场源区域(0 m,0 m,0 m)~(1200 m,1200 m,1200 m),剖分个数为240 × 240 × 240,网格间距为5 m × 5 m,观测点个数为240 × 240,观测面高度z0=-10 m,z轴垂直向下为正.如图5a所示,球异常体的中心位置(600 m,600 m,600 m),半径为200 m,异常体磁化率κ=0.03 SI,背景磁化率为0 SI,正常场大小T0=50000 nT.计算机参数为:AMD Ryzen 7 3700X 3.59 GHz(CPU),内存32 GB.
表2为垂直磁化时传统解析解,Gauss-FFT算法和快速算法的计算性能比较.快速算法计算ΔT总耗时约2.67 s,其中核矩阵耗时约0.29 s,核矩阵与磁化率向量的乘积耗时约2.38 s,内存需求约111.29 MB(其中,三维磁化率向量约110.59 MB,核矩阵约0.23 MB,中间变量约0.47 MB),快速算法的内存组成部分可参考表1.相同的模型,快速算法的计算效率比传统解析解方法快约1.55×105倍,比4点Gauss-FFT算法快约23倍,8点Gauss-FFT算法时扩大到了94倍,而且快速算法的计算精度比4点和8点的Gauss-FFT算法更高,其中4点Gauss-FFT算法的最大绝对误差比其他三种算法大几个数量级.以上可知,本文改进的快速算法在计算性能方面具有显著优势.此外,由表1可知,在开展磁异常反演时,若采用传统解析解方法进行正演,则反演时需存储的核矩阵约6.37×106MB,而采用快速算法仅约55.53 MB,内存需求降低了约1.15×105倍.图5b、c分别为传统解析解和快速算法的ΔT正演结果,图5d为快速算法正演结果的绝对误差,最大绝对误差仅约1.01×10-6nT.
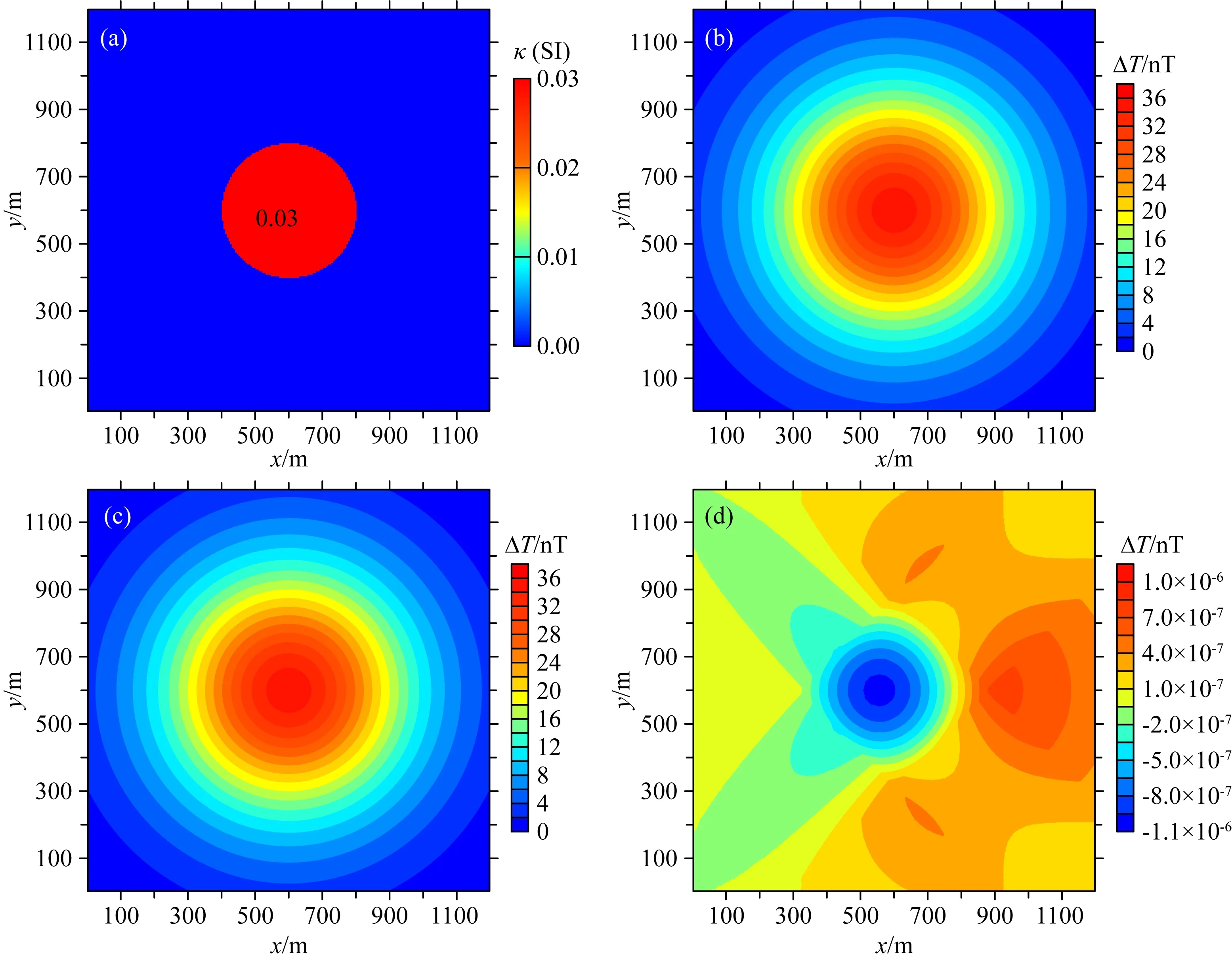
图5 垂直磁化时球异常体的模型及其ΔT正演结果(a)球异常体在z=-600 m处切面的磁化率分布;(b)传统解析解的计算结果;(c)快速算法的计算结果;(d)快速算法计算结果的绝对误差.Fig.5 A spherical anomalous model and the ΔT results and the errors under perpendicular magnetization(a)The susceptibility distribution in the section at z=-600 m;(b)—(d)are the ΔT results of the traditional analytical solution,the proposed method,and the absolute errors.

表2 垂直磁化时传统解析解,Gauss-FFT算法和快速算法的计算性能比较Table 2 Comparison of computational performance between the traditional analytical solution,Gauss-FFT algorithm,and the proposed method under perpendicular magnetization
类似的,当计算ΔTx时快速算法总耗时约2.50 s,其中核矩阵耗时约0.14 s,核矩阵与磁化率向量的乘积耗时约2.36 s,快速算法分别比传统解析解方法、4点和8点Gauss-FFT算法快约3.05×104倍、26倍和105倍.图6为传统解析解和快速算法的ΔTx正演结果以及快速算法正演结果的绝对误差,最大绝对误差仅约5.03×10-9nT/m.

图6 垂直磁化时球异常体的ΔTx的正演结果和误差(a)传统解析解的计算结果;(b)快速算法的计算结果;(c)快速算法计算结果的绝对误差.Fig.6 The forward modeling results (ΔTx)and the error for the spherical anomalous body under perpendicular magnetization(a)—(c)are the ΔTx results of the traditional analytical solution,the proposed method and the absolute error.
2.2 倾斜磁化模型
为了验证快速算法在倾斜磁化情况下的计算性能,仍采用上述球异常体模型,计算该模型在倾斜磁化下(I0=I=45°、A0=A=5°)的ΔT和ΔTx.
表3为倾斜磁化时传统解析解,Gauss-FFT算法和快速算法的计算性能比较.快速算法计算ΔT总耗时约31.89 s,其中核矩阵耗时约29.19 s,计算ΔTx总耗时约8.45 s,其中核矩阵耗时约5.77 s.对比表2,在垂直磁化和倾斜磁化两种情况下,传统解析解方法和8点Gauss-FFT算法的计算性能几乎不变.计算ΔT时快速算法分别比传统解析解方法和8点Gauss-FFT算法快约1.33×104倍和7倍,计算ΔTx时则快约1.02×104倍和31倍.由于高斯点数的减少,4点Gauss-FFT算法比8点Gauss-FFT算法快约3倍,但计算精度较低.图7分别为倾斜磁化时ΔT和ΔTx的正演计算结果和误差,可知快速算法的计算精度很高.

表3 倾斜磁化时传统解析解,Gauss-FFT算法,和快速算法的计算性能比较Table 3 Comparison of computational performance between the traditional analytical solution,Gauss-FFT algorithm and the proposed method under oblique magnetization
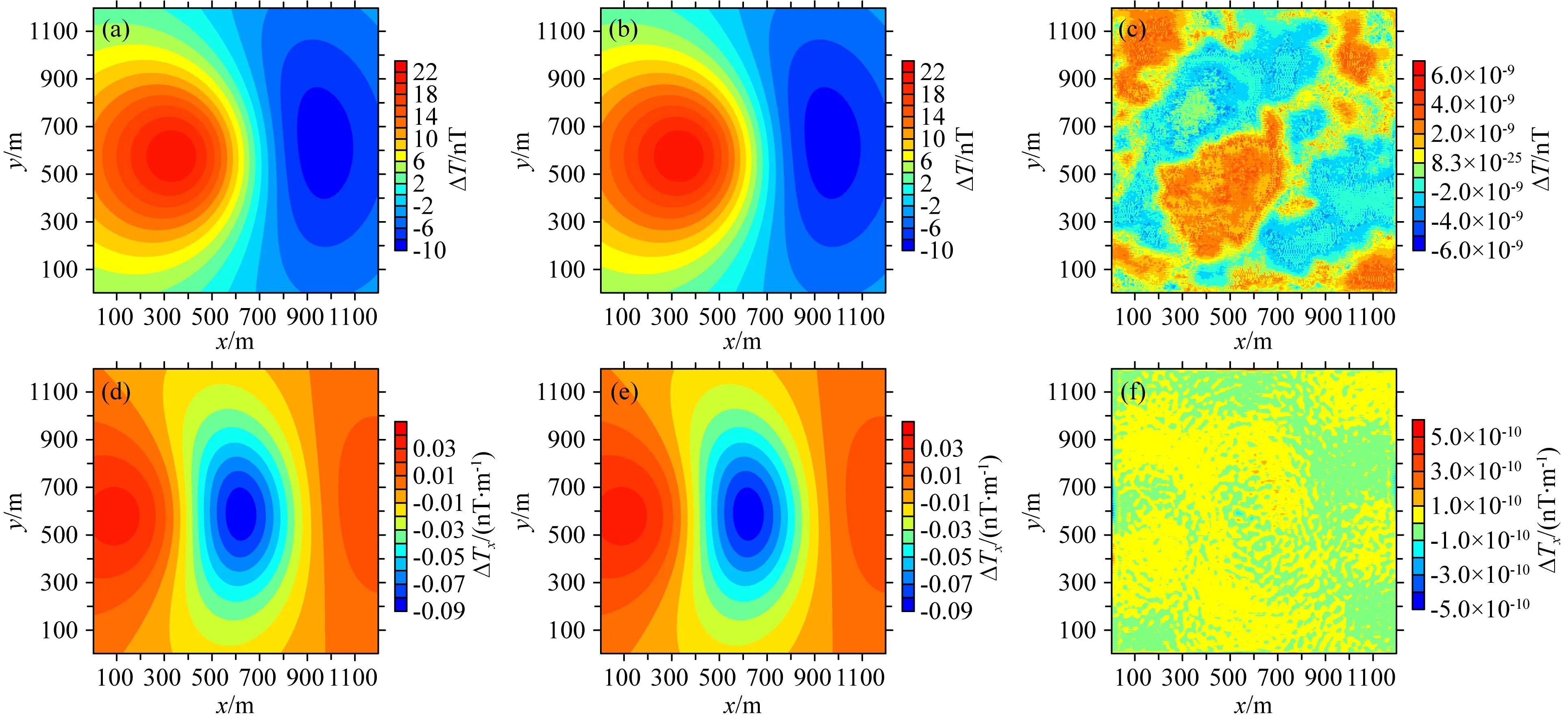
图7 倾斜磁化时球异常体的ΔT和ΔTx的正演结果和误差(a)(d)、(b)(e)、(c)(f)分别为ΔT和ΔTx的传统解析解的结果,快速算法的结果及其绝对误差.Fig.7 The forward modeling results (ΔT and ΔTx)and their errors for a spherical anomalous body under oblique magnetization(a)(d),(b)(e),(c)(f)are the ΔT and ΔTx results of the traditional analytical solution,the proposed method and the absolute errors.
图8分别对比了传统解析解,8点Gauss-FFT算法,和快速算法在计算ΔT和ΔTx时的相对计算时间随剖分个数的变化关系,均采用最长的计算时间进行了归一化处理.随着剖分个数增加,正演耗时呈指数增加,而且水平方向上的剖分个数越多,快速算法相比于传统解析方法提升的计算效率越高.从图8a可知,当计算垂直磁化下的ΔT且各方向剖分个数为240时,快速算法比传统解析解方法快约5个数量级,比8点Gauss-FFT算法快约两个数量级.此外,垂直磁化下的快速算法比倾斜磁化下的快约一个数量级.图8b具有类似的性质,这也验证了快速算法的高效.
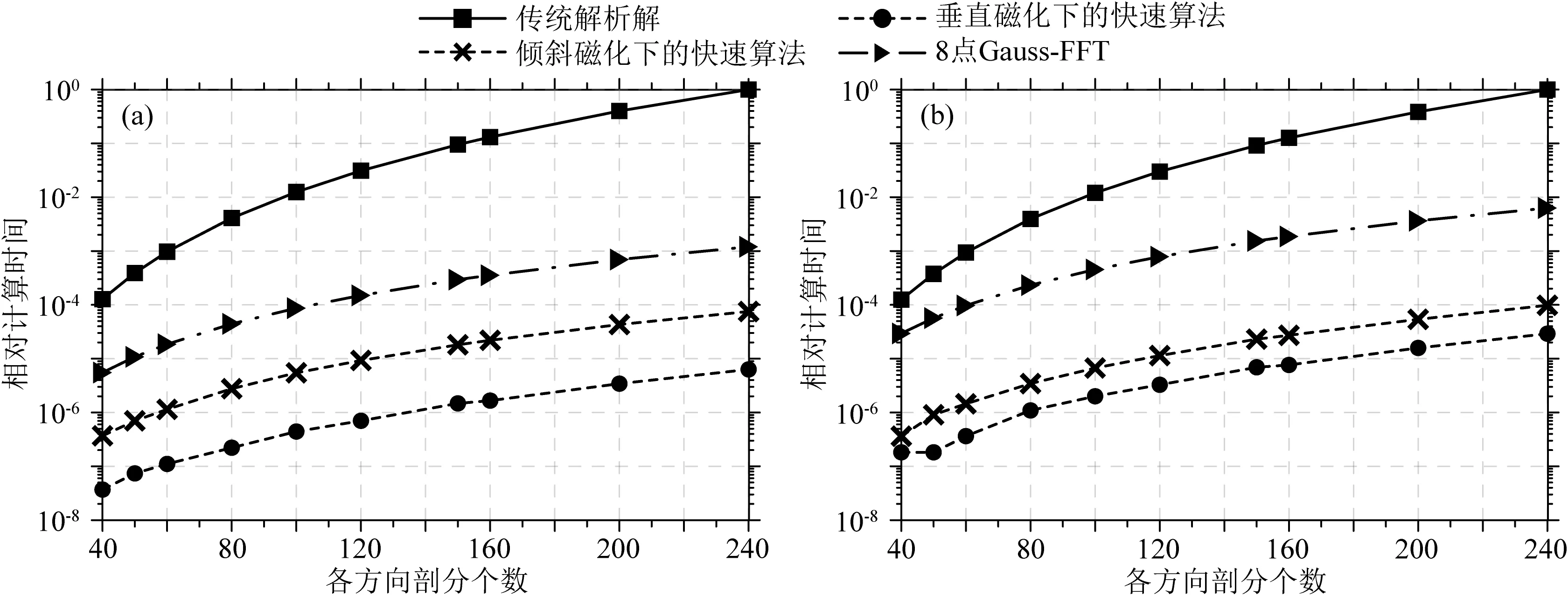
图8 快速算法与传统解析解、Gauss-FFT的相对计算时间对比(a)和(b)分别为ΔT和ΔTx的相对计算时间对比,都采用最长的计算时间进行了归一化处理.Fig.8 Comparison of the relative computation time between the traditional analytical solution,Gauss-FFT algorithm,and the proposed methodThe time of ΔT (a)and ΔTx (b)is normalized by the longest computation time.
图9分别为垂直磁化和倾斜磁化时快速正演ΔT和ΔTx的总耗时,计算核矩阵的耗时,和核矩阵与磁化率向量的乘积耗时随剖分个数的变化关系.从图9a、b可知,在垂直磁化下快速正演ΔT,计算核矩阵的耗时比核矩阵与磁化率向量的乘积耗时低约一个数量级,而倾斜磁化时相反.从图9c、d可知,快速正演ΔTx时也存在类似现象.值得注意的是,垂直磁化和倾斜磁化下,快速正演中计算核矩阵与磁化率向量的乘积耗时几乎一样,而计算核矩阵耗时存在明显差异.这种差异既源于垂直磁化时特殊的BTTB矩阵的结构特性,也得益于中间变量的引入.可以看出,快速算法通过改进核矩阵的计算过程,将正演总耗时压缩到跟核矩阵与磁化率向量的乘积耗时相同水平.
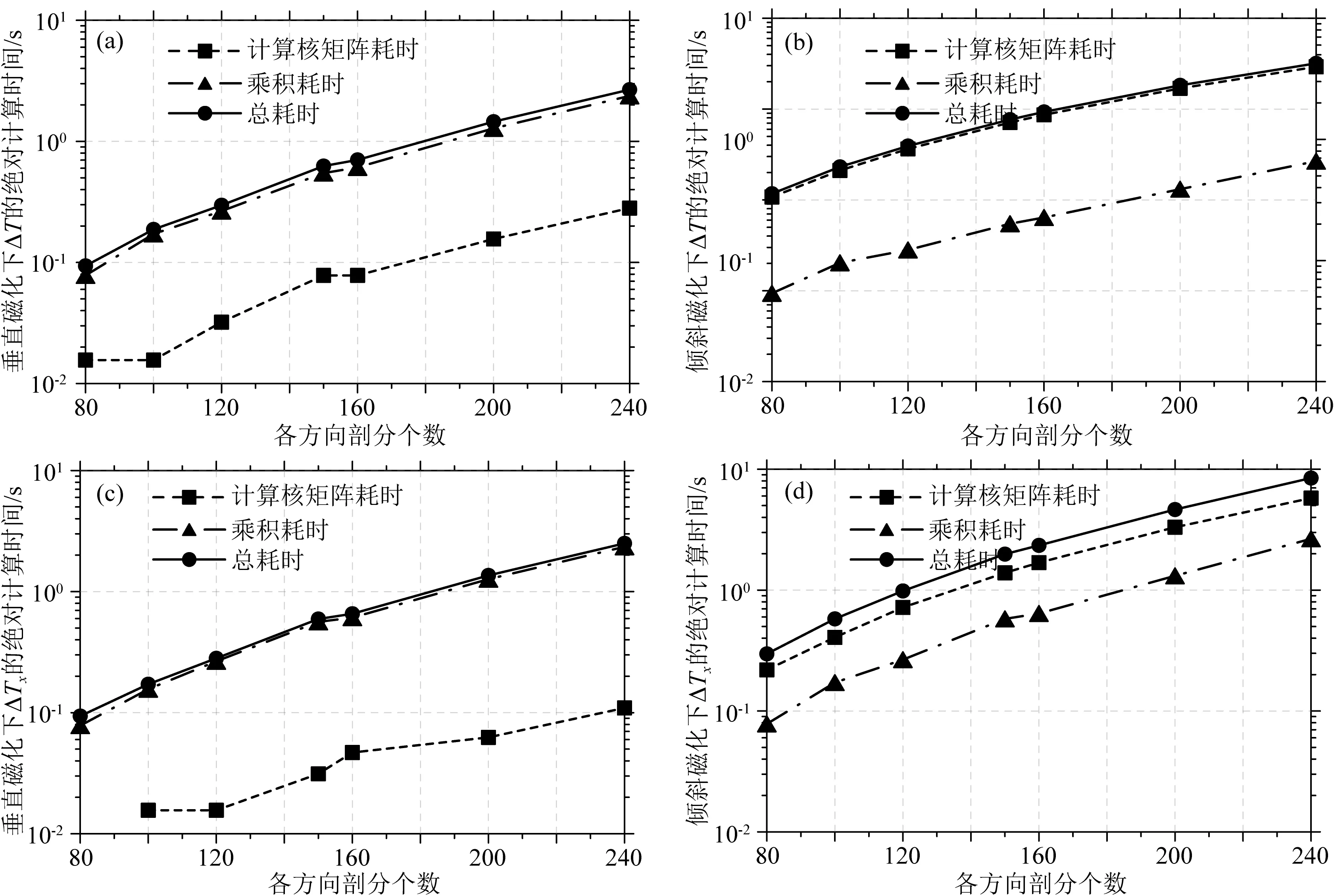
图9 快速算法计算ΔT和ΔTx的绝对计算时间(a)(c)、(b)(d)分别对应ΔT和ΔTx在垂直磁化和倾斜磁化下的绝对计算时间.图(c)的计算核矩阵耗时曲线,当各方向剖分个数为80时实测耗时为0,故缺省.Fig.9 The absolute computation time of ΔT and ΔTx by the proposed method(a)(c),(b)(d)represent ΔT and ΔTx under perpendicular magnetization and oblique magnetization,respectively.As for the time-consuming curve of calculating nuclear matrix in figure (c),when the number of divisions in each direction is 80,the measured time-consuming is 0,so it is defaulted.
3 应用
3.1 基于快速正演的聚焦反演
为了验证快速正演算法的实用性,本文将提出的快速正演运用于磁异常数据的聚焦反演,并对比了传统聚焦反演方法与加入了快速正演算法的聚焦反演方法在计算效率和内存需求方面的差异.
针对位场反演的非唯一性,Tikhonov和Arsenin(1977)提出的正则化反演目标函数为:
φ=φd+βφm,
(30)
其中φd为数据目标函数,定义为:

(31)
其中Wd为数据加权矩阵,Wd=diag[1/ε],其中εi为第i个观测数据误差的标准差.dobs为磁异常观测数据,β为正则化参数.φm为模型目标函数,Portniaguine和Zhdanov(1999)提出了最小支撑稳定函数用来进行聚焦反演.为了减少聚焦反演迭代次数,本文采用Rezaie(2020)改进后的sigmoid稳定函数进行反演:
(32)
其中σ为聚焦参数,一般取接近于0的小数.模型目标函数可以用L2范数表示为:

(33)
Ws为模型加权矩阵,可表示为:
Ws=diag[(1+exp(-κ2/σ2))(κ2+σ2)]-0.5,
(34)
Wz为深度加权矩阵,Wz=diag[1/z1.5],其中z为模型参数的深度(Li and Oldenburg,2003).
利用上述公式,可得转换后的反演目标函数:

(35)
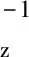
将公式(35)右边第一项展开得到:

=[(Gwκw)T-(dw)T](Gwκw-dw)
=[(κw)T(Gw)T-(dw)T](Gwκw-dw)
=(κw)T[(Gw)T(Gwκw-dw)]
-(dw)T(Gwκw-dw),
(36)
其中最消耗内存和计算时间的部分,即Gwκw中核矩阵和磁化率向量的乘积运算Gκ,以及(Gw)T中核矩阵的转置GT和Wd的乘积运算,都引入快速正演方法优化了核矩阵内存需求,并提升了计算效率.
为了使目标函数公式(35)最小,Portniaguine和Zhdanov(1999)提出了重加权正则化共轭梯度法(Reweighted Regularized Conjugate Gradient,RRCG)计算最优解κw.本文采用RRCG算法的进行反演,详细实现过程可参考Rezaie(2020),同样加入了自适应正则化方法并强制约束模型参数的上下边界.停止迭代的判断条件为:
(37)
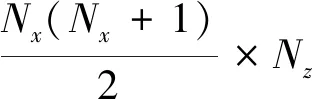
3.2 反演模型试验
本节采用合成模型进行测试,反演垂直磁化下的磁异常ΔT.场源区域(0 m,0 m,0 m)~(600 m,600 m,300 m),剖分个数120×120×60,网格间距5 m×5 m,观测点个数120×120,观测面高度z0=-0.1 m,z轴垂直向下为正.阶梯异常体模型在z=50 m和y=300 m处的磁化率分布分别如图10a、b所示.首先,利用上述基于BTTB矩阵的快速正演算法,计算该模型在观测面上产生的理论磁异常ΔT,并加入均值为零,标准差为5%理论值最大值的高斯随机噪声,作为反演的观测数据,磁异常如图10c所示.
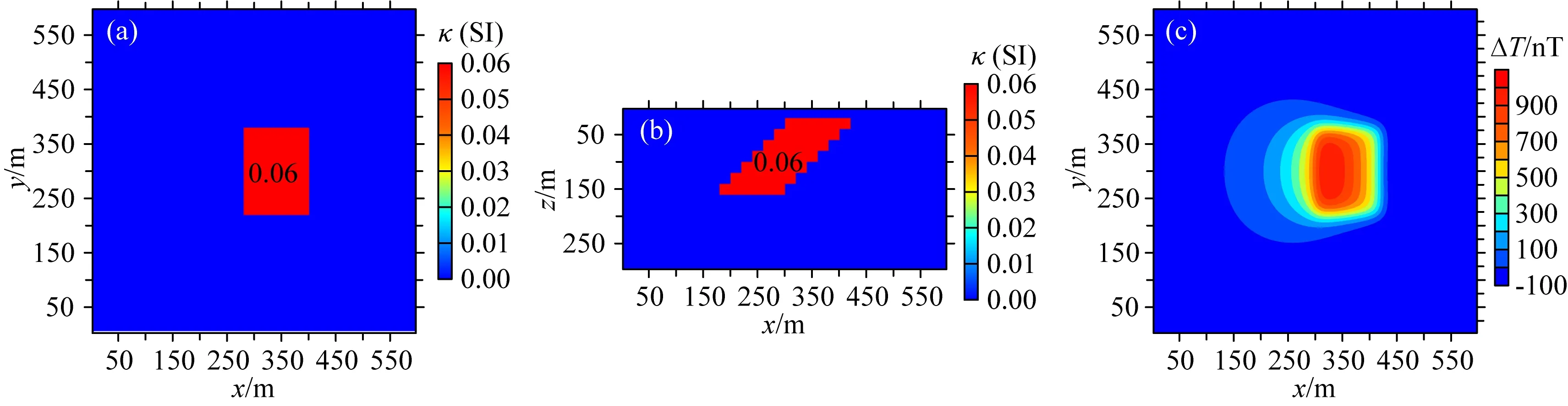
图10 真实模型磁化率分布及其产生的磁异常ΔT(a)z=50 m切面磁化率分布;(b)y=300 m断面磁化率分布;(c)加入了高斯噪声的观测数据.Fig.10 The synthetic model and its ΔT result(a)Magnetic susceptibility distribution on horizontal section z=50 m;(b)Magnetic susceptibility distribution on longitudinal cross profile x=300 m;(c)Observation data adding Gaussian random noises.
反演计算中,采用的聚焦参数σ为0.005,磁化率约束范围为0 ~ 0.06 SI,自适应正则化的衰减系数为0.6,收敛阈值δ为10-3.最终反演迭代了1018次,反演结果在z=50 m和y=300 m处的磁化率分布分别如图11a、b所示.可以看出,使用RRCG算法的聚焦反演能较好的拟合真实模型的磁化率,顶面,底面和走向.另外,测试发现,聚焦参数和强制约束模型参数的上边界的选取都对反演结果影响较大.
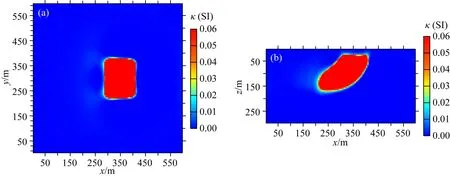
图11 模型反演结果(a)z=50 m剖面上反演结果;(b)y=300 m断面上反演结果.Fig.11 Inversed magnetic susceptibility distribution of the model(a)Inversed result in z=50 m section;(b)Inversed result in y=300 m profile.
为了对比传统反演方法与快速反演方法的计算效率,分别测试两者在反演过程中迭代一次的耗时,传统反演耗时约568.13 s,快速反演耗时约0.84 s,减少了6.75×102倍.另外,传统反演的核矩阵内存需求约为9.95×104MB,快速反演则约为3.48 MB,降低了约2.88×104倍.为了能进一步对比更大的模型,可利用等效性压缩核矩阵的内存,解除物理内存对传统反演方法的使用限制.当剖分个数为240×240×120,观测点个数为240×240时,在其他反演参数不变的情况下,反演结果几乎不变.此时,迭代一次,传统反演耗时约2.36×104s,快速反演耗时约7.42 s,相差3.18×103倍.
4 结论
针对传统空间域三维磁场正演计算效率较低的问题,本文改进了空间域三维磁场正演算法,使其具备高精度和高效率的优点,并将其运用到磁场反演中.基于均匀网格剖分,该正演方法先利用BTTB矩阵和等效性压缩核矩阵,通过引入中间变量减少重复计算,再基于BTTB矩阵和FFT的快速算法进一步提高计算效率.得到以下结论:
(1)正演球异常体模型的实验表明,计算ΔT时,垂直磁化下快速算法比传统解析解快约1.55×105倍,比8点Gauss-FFT算法快约94倍,最大绝对误差约为1.01×10-6nT;倾斜磁化下则分别快约1.33×104倍和7倍,最大绝对误差约为5.54×10-9nT.证明了快速算法具有计算效率高、精度高的优点.另外,快速算法在垂直磁化时提升的计算效率比倾斜磁化时更高,说明改进核矩阵的计算过程对于提升计算效率有很大帮助.
(2)将快速正演算法引入到反演方法中,并且利用快速正演优化了反演中有核矩阵参与计算的部分.合成模型的反演结果表明,加入了快速正演算法的反演方法比传统反演方法快了约6.75×102倍.同时,核矩阵的内存需求降低了约2.88×104倍.这也证明了快速算法具有内存需求小的优点.
(3)事实上,计算时间和内存需求最终取决于剖分个数.随着剖分个数增加,正演耗时呈指数增加,而且水平方向上的剖分个数越多,快速算法比传统解析解方法提升的计算效率越高.相应的,反演时压缩的核矩阵内存越多.本文算例均采用串行计算,由于在深度方向上为逐层计算再累加求和,计算高度并行,若采用并行,计算效率还将进一步提高.鉴于快速算法在计算效率上的显著优势,还可将其用于大规模重力场正反演和位场延拓等处理计算,具有广阔的应用前景.
致谢感谢三位匿名审稿人提供的建设性的意见和建议,使本文更加完善;感谢陈龙伟教授、杜劲松教授和孙石达博士在论文研究开展过程中提供的帮助和宝贵建议.
附录A
将水平观测面均匀剖分成nx×ny个网格,将场源区域均匀剖分成nx×ny×nz个长方体单元,即垂直方向剖分成nz层,每一层在水平面又剖分成nx×ny个长方体单元.假设磁化率为1,此时磁异常值只与观测点与长方体单元的位置有关,计算第一层单元体产生的磁异常值.
第一层的第一个长方体单元对所有观测点的磁异常用T(1,1)表示:
(A1)
其中,元素的上标为长方体单元坐标,下标为观测点坐标,i=1,…,nx,j=1,…,ny.仅当nx=ny时,T(1,1)才为方阵.
将T(1,1)转换为列向量:
T(1,1)=vec(T(1,1))
(A2)
以此类推,依次求出第一层剩下的所有长方体单元对所有观测点的磁异常,同样用列向量表示.
第一层所有长方体单元对所有观测点的磁异常值用T1表示:
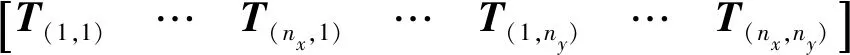
(A3)
其中T1为BTTB矩阵,可以表示成T1=BTTB(t),其中:
(A4)
得到大小为(2nx-1)×(2ny-1)的矩阵t是算法非常关键的一步.
设真实磁化率为

(A5)
令:
(A6)
公式(A5)可用二维离散卷积表示为:
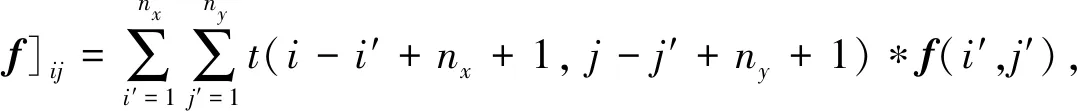
(A7)
其中,i=1,…,nx,j=1,…,ny,即:
(A8)
而二维离散卷积可以利用FFT加速算法.
首先将t在复数域扩展为:
(A9)
令:
(A10)
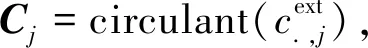
(A11)
令:
(A12)
再将磁化率进行扩展:
(A13)
令g=Cextvec(fext),运用FFT计算,其中:
g=Cextvec(fext)=vec(F-1{F{cext}*F{fext}})=vec(ifft(fft2(cext).*fft2(fext))),(A14)
令g′=array(g),抽取g′的前nx×ny个元素并排列成列向量就得到h1.类似的,将每一层长方体单元的磁异常进行叠加得到总的磁异常.
