基于局部采样MCMC方法的时移探地雷达反演

王升超，韩立国，巩向博，张盼

吉林大学地球探测科学与技术学院，长春 130026

0 引言

马尔科夫链蒙特卡洛方法(MCMC)是基于数学概率分布模拟的一种方法，目前已经广泛应用于理论物理、信号通信、医学等领域，在地球物理领域的应用也在不断的发展中，特别是应用于地球物理反演问题(Grandis et al.,1999;Malinverno and Leaney,2000).相比于其他反演方法，MCMC方法的优点在于全局寻优，不会陷入局部极小，并且不依赖于准确的先验模型，可以引入更为复杂的先验信息.

对于地球物理反演问题，基于最小二乘的方法得到了广泛的应用，Menke(1989)提出了确定性最小二乘法，而Tarantola和Valette(1982)提出了最小二乘的概率反演方法，在贝叶斯框架下，反演问题的解是一个概率密度函数，称之为后验概率密度函数.Hansen等(2006)提出了一种基于连续模拟的线性走时层析成像的概率反演方法，他们利用了经典最小二乘反演和克里格法(Journel and Huijbregts，1978)的等价性.Nielsen等(2010)给出了这种方法在井间探地雷达数据中的应用.Gloaguen等(2005a，b)提出了一种基于克里格法的误差模拟的相关方法，相当于概率最小二乘法，并将其应用于井间探地雷达层析成像.Giroux和Gloaguen(2012)将这种方法用于各向异性速度场的反演.这些方法仅对严格线性反演问题有效，并且依赖于描述噪声模型和先验模型的高斯统计的固有假设，先验模型必须以高斯形式给出，先验模型由均值和协方差模型定义.国内，张广智等(2011)将MCMC方法应用于叠前地震数据反演，在波阻抗反演方面取得了一定效果.殷长春等(2014)将概率反演的方法应用到航空电磁领域，克服了初始模型的影响，成功反演了深度低阻层.王朋岩等(2015)成功使用MCMC方法反演了岩性参数.孙月成(2018)则将基于MCMC 算法的地质统计学反演应用在油藏模拟当中，取得了良好的效果.

但在实际反演问题当中，先验信息往往比高斯模型描述的更为复杂，而且先验信息也不能用准确的数学公式表达.Hansen等(2008b)展示了拓展的Metropolis算法(Mosegaard et al.，1995)在非线性井间层析成像问题中的应用，其中先验模型是非高斯的，并可以由任何地质统计学方法定义.扩展的Metropolis算法不需要先验信息的准确数学表达式，可以用来采样后验概率密度函数，包括高度非线性的反演问题.在拓展的Metropolis算法中，只要有一个能够对先验概率密度函数进行采样的“黑箱”算法，就可以完成对先验信息的采样任务.Hansen等(2008a,2012)提出了连续吉布斯采样的方法，连续吉布斯算法在采样先验信息时，可以有效的控制扰动的步长，具有很高的采样效率(Gómez-Hernández and Journel，1993).这样，将连续吉布斯采样作为一种“黑箱”算法应用于拓展的Metropolis算法中，使得在进行概率反演时，对先验模型的选择变得非常灵活(Journel and Zhang，2006)，可以对任何地质统计学算法定义的先验信息进行采样，既可用于相对简单的两点统计模型(例如基于高斯的先验模型)，也可以用于更复杂的多点的统计模型，通过多点算法可以灵活地模拟高熵、低熵结构或其组合的实现，使得在求解概率反演时，可以引入更复杂的先验模型信息(Hansen et al.,2013).

后验概率分布的求解是通过模型提供的先验信息，数据的不确定性和模型参数等综合求解.其中所有可用的先验信息都由先验概率密度函数描述.多种信息综合反映了后验样本模型的变化，为后验采样提供了依据.概率反演方法除了能提供后验模型参数的协方差外，也可以解决复杂的问题，如地质连通性的概率或流体的停留时间(Mosegaard,1998).

作者将讨论使用MCMC方法对井间探地雷达(GPR)数据进行初至走时的时移反演问题，探地雷达(GPR)井间层析成像也是近地表地质构造和地球物理参数层析成像的常用方法.这种走时数据对电磁波速的地下变化很敏感，这与介电常数有关，而介电常数受地下含水量的强烈影响(Topp et al.，1980).因此，时移探地雷达反演结果可以反映地下含水量在不同时间的变化.

时移反演有两种反演策略，称为连续反演法和双差法(Waldhauser and Ellsworth，2000)，Huang等(2020)在双差法的基础上实现了基于目标导向的全波形时移反演，提高了时移反演的计算效率.两种方法的主要区别在于双差法减小了非目标区的影响，提高了目标区的反演精度.在时移反演中，作者使用双差法结合MCMC方法对探地雷数据进行反演.对于时移探地雷达数据，要解决目标位置的变化，需要对两组数据在不同观测点进行至少两次反演计算.两次反演计算量大，非目标区域的反演也会影响目标区域的精度.为了解决这个问题，作者采用了局部采样的MCMC反演方法，在双差法的第二次反演过程中，采用局部采样即只对目标区域采样的方法代替了全局采样法.这样，减少了非采样区域对时移位置的影响，在提高计算效率的同时，增加了目标区域的反演精度.

本文中，作者演示了如何通过使用拓展的Metropolis算法结合使用连续吉布斯采样的地质统计学算法定义的先验信息对时移的探底雷达数据实现MCMC的反演.将MCMC方法应用于探地雷达时移反演中，首先利用连续吉布斯采样和Metropolis算法对反演问题进行求解.然后，结合双差法得到目标区域的变化.作者将该方法应用到GPR模拟数据中，测试该方法的效果，分析对比了局部采样的MCMC反演和全局采样的MCMC的反演误差，证明了局部采样MCMC反演的有效性.

1 MCMC反演

1.1 概率反演公式

对于地球物理反演问题，地下构造可以用一组模型参数m来表示，观测数据可以用一组数据d来表示.正演问题是指通过一个函数映射f来获取观测数据d(Tarantola and Valette，1982)：

d=f(m)，

(1)

函数f通常基于相应的物理关系，对应的反演问题的公式可以表示为

m=f-1(d)，

(2)

求解反演问题的主要困难是如何而求解反演算子f-1，实际操作中会出现反演算子难以求解或者不存在的情况，此外，正演算子f是基于对正确物理关系的某种近似，有一定的误差.在GPR反演的研究中，模型m代表了地下速度的层析成像结果，观测数据是波在发射源和接收器之间的走时.

反演问题是通过先验信息来获取模型参数，基于概率方法的反演公式可以表示为

σM(m)=kρM(m)L(m)，

(3)

反演问题的解σM(m)是后验概率分布，其中k是归一化因子.先验概率密度ρM(m)描述了与数据无关的模型参数先验信息.L(m)是似然函数，它是一种概率的度量，用于衡量给定模型相关参数与给定观测数据不确定性模型的匹配程度，具体公式为

(4)

ρD(g(m))描述测量的不确定性，通常与记录数据的仪器中的不确定性有关.θ(d|m)表示由于使用不完善的正演方法或不完善的参数化而引起的建模误差.μD(d)描述信息的统一性，以确保参数化对坐标系中的更改保持不变.在大多数情况下，我们可以假设μD(d)是一个常数.

1.2 基于射线的正演方法

求解探地雷达(GPR)数据初至走时的反演问题时，正演的观测数据是走时，也就是波在发射源和接收器之间的传播时延.关于走时的计算，有几种类型的正演方法，我们使用基于程函方程的方法(Hassouna and Farag,2007).在程函方程中，沿曲线u(x)的到达时间，以速度场m(x)定义传播速度(Sethian and Popovici，1999)：

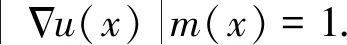
(5)

快速推进法是一种具有高精度、高效率、无条件稳定等特性的走时计算方法(孙章庆，2008)，利用多阶快速推进法可以有效的求解程函方程.这种正演模型是非线性的，因为程函方程对应于波动方程的高频近似，通常被称为高频射线近似.信号源和接收器之间的走时d可由式(6)给出：

(6)

其中G(x)是灵敏度核，它描述了每个模型参数(在Fresnell区内)对走时的灵敏度.G(x)可以在广泛的假设下计算，我们利用波动方程的高频近似来计算灵敏度核G(x)，灵敏度核可以用连接源和接收器的射线来描述，这种类型的正演模型称为基于射线的正演模型.

1.3 拓展的Metropolis 算法

在现实中，大多数地球物理反演问题都是非线性的，而且用非高斯统计来描述.我们需要一种不需要先验概率密度显式表达式的算法.拓展的Metropolis算法可以通过使用连续的吉布斯采样作为黑箱算法来解决这个问题，黑箱算法能够在先验概率密度足够的情况下执行随机游走(Mosegaard and Tarantola，1995).拓展的Metropolis算法包含两个主要的步骤：

(1)提出了一个候选模型mpro，它是在当前模型mcur中给出一个扰动后产生的新模型，同时也是先验概率密度函数的一次实现.

(2)决定接受或是拒绝当前的模型，模型的接受依据Metropolis算法的接受概率：

(7)

式中，L(mpro)/L(mcur)为候选模型与当前模型之间的似然函数之比.如果接受，则候选模型取代当前模型，即达成了一个后验概率密度采样的实现.否则，候选模型将被拒绝，当前模型将再次循环，所以在每次迭代中，后验概率密度的样本量都会增加.然而，基于MCMC的采样方法计算量大，对于时移反演问题，需要对两个时刻分别进行反演，进一步增加了计算量，并且非标区域的反演会影响目标区域的精度.针对这一问题，作者使用了局部采样的MCMC反演方法，在时移反演的第二次反演时，只对目标区域进行采样，减少了计算量，提高了目标区域的反演精度.

局部采样的MCMC反演将依靠作为扩展Metropolis算法一部分的连续的吉布斯采样器完成.我们使用连续的吉布斯采样器对ρM(m)直接采样.流程如下：

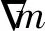
(2)计算当前模型和候选模型的似然函数，L(mcur)和L(mpro).

(4)如果建议的模型被接受，那么用mpro代替当前模型mcur的转换被接受，即mcur=mpro，否则，仍然在mcur位置，再次产生一个随机扰动进行下一次迭代.

2 双差法时移反演

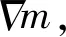
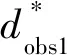
本文主要采用双差法来解决时移反演问题，在双差法的第二次反演时，采用局部采样的MCMC方法进行反演，该双差法的主要流程如图1所示.

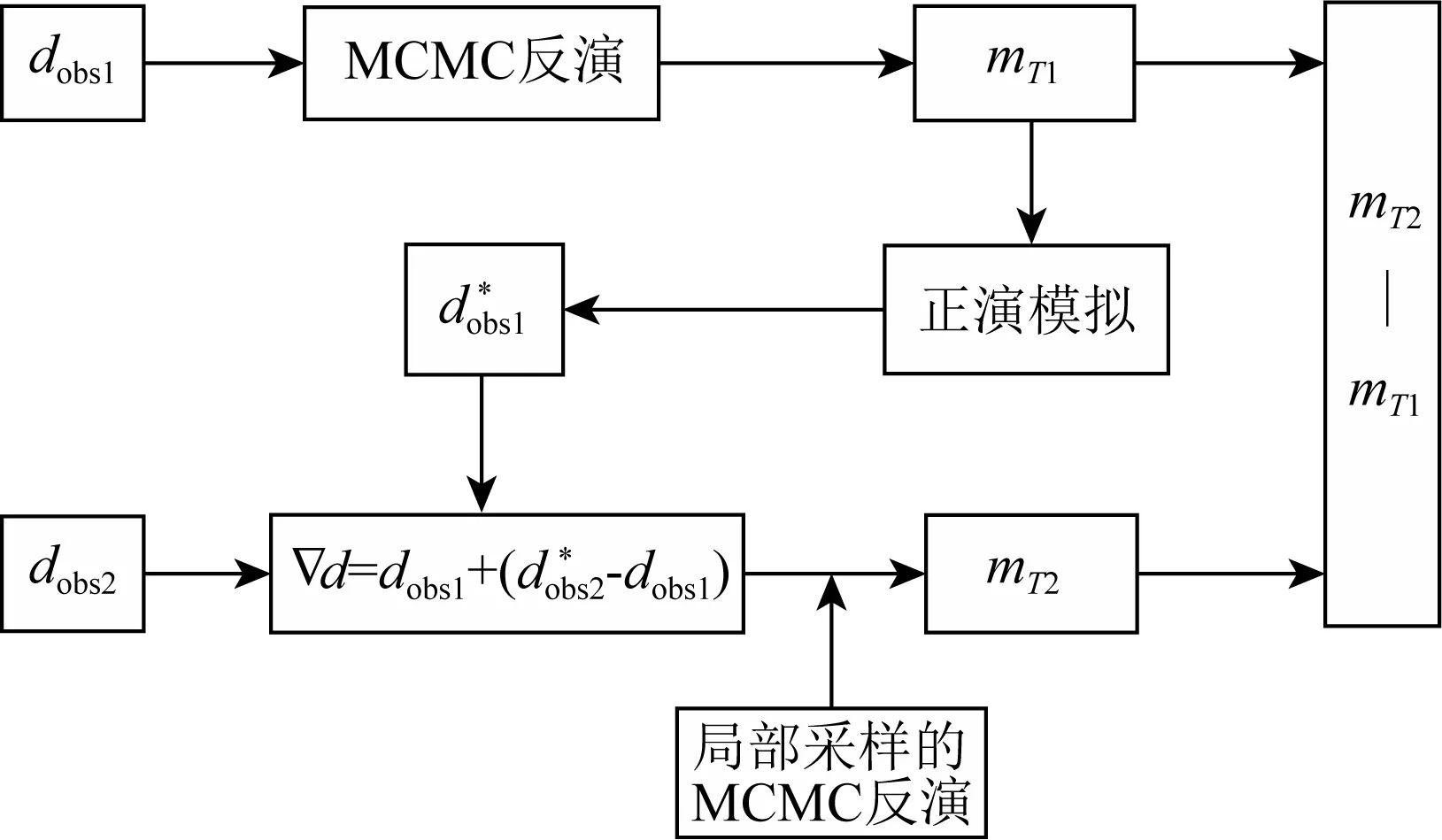
图1 双差法时移反演流程图Fig.1 Double difference strategy

3 合成的GPR数据测试

为了验证该方法的有效性，我们模拟了一个合成的探地雷达数据，由一个平均速度为1.45×10-1m·ns-1的多变量高斯概率分布生成的7 m×13 m(87×47像素，0.15 m×0.15 m)的参考模型mT1，方差为3×10-4m2ns-2，其球形协方差模型具有6 m的各向同性范围，这与Looms等(2010)和Hansen等(2013)的观测系统和参数设置是相似的.图2显示了探地雷达(GPR)钻孔记录的观测系统，其中红色的点为发射源，黑色圆点为接收器，总共ND=702对.

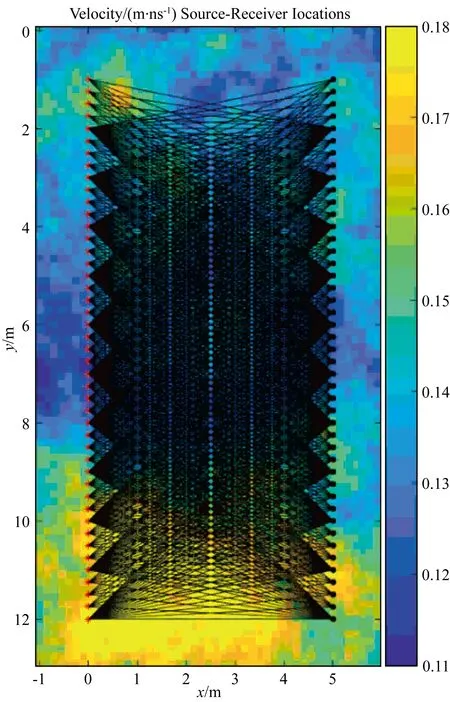
图2 数据观测系统分布，共702组发射源和接收点组合Fig.2 Recording geometry,ND=702 pairs of sources (red crosses)and receivers (black dots)are represented by a connecting black line

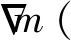
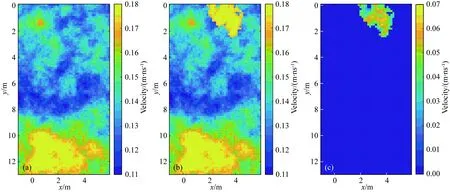
图3 起始速度模型mT1，监测速度模型mT2和速度扰动Fig.3 Initial model mT1,monitor model mT2 and the perturbation

使用速度模型mT1和mT2正演模拟获得相应的初至时间数据data1 和 data2作为观测数据，图4显示了相应的正演数据分布，其中黑色曲线代表data1，红色曲线代表data2.由图4可以看出，两组正演数据的变化趋势大体相同，只在局部位置有差异，可以认为是速度扰动区域在正演数据中产生的影响.

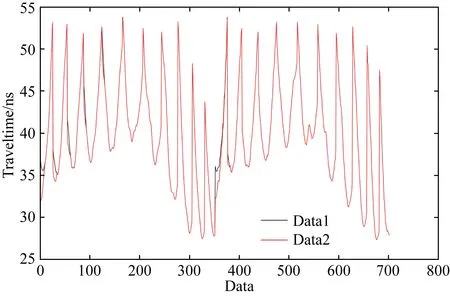
图4 正演模拟的初至走时数据Fig.4 The simulated traveltime data1 and data2

在反演之前，首先要根据先验信息对先验概率密度函数进行采样，先验采样是一个随机过程，任何满足先验条件的模型都有可能出现.图5显示了对先验概率密度函数进行连续吉布斯采样后，得到的五个独立实现的先验速度模型，由图5可以看出，每个先验模型的速度分布各不相同.

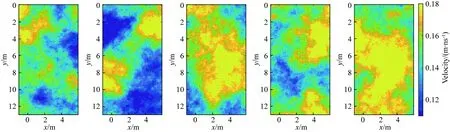
图5 先验概率密度函数的五个独立随机采样结果Fig.5 Five statistically independent realizations of the priori probability density

在时移反演中，为了求得时移位置的变化，我们首先对起始时刻T1的观测数据data1进行MCMC反演，用拓展的Metropolis算法采样获得后验概率密度函数的样本.图6展示了五个后验采样样本，样本中可以明显看出速度分布浅层主要为低速的蓝色，深层为高速的黄色，与给出的速度模型mT1特征一致.

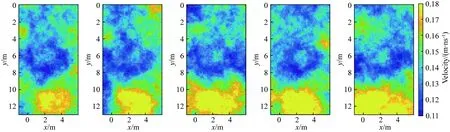
图6 后验概率密度函数的五个采样样本Fig.6 Five statistically independent realizations of the posterior probability density

为进一步检验反演的准确性，我们对这些后验采样得到的模型进行正演模拟，正演的走时数据如图7所示，其中红色曲线为观测数据data1，黑色曲线为多个后验采样模型的正演数据.可以发现，通过拓展的Metropolis算法获得的后验样本，其正演的结果与观测数据data1有很高的一致性，证明了反演的方法的有效性.

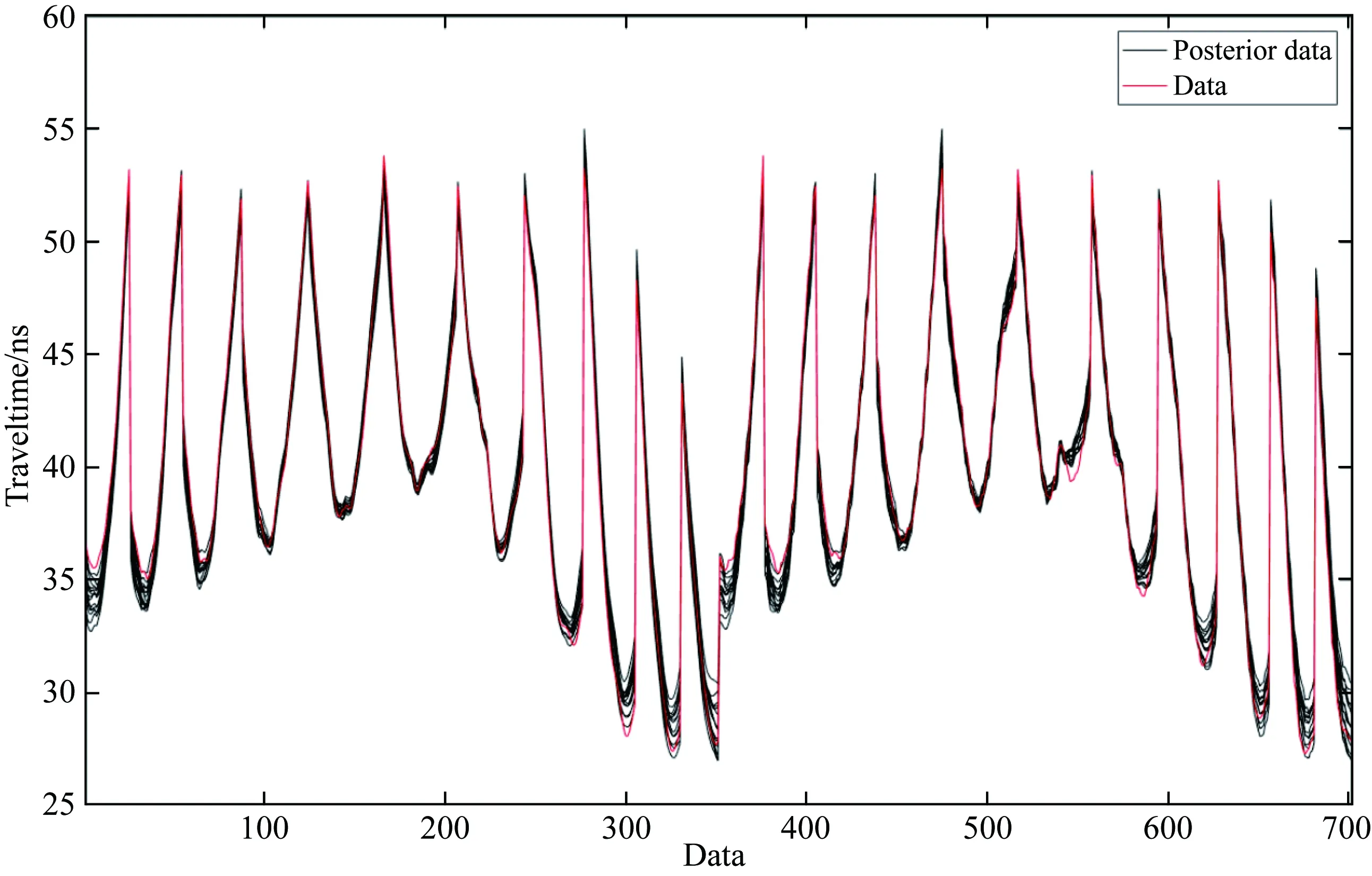
图7 后验样本正演得到的走时数据Fig.7 The traveltime data of data and posterior

双差法时移反演中，第二次反演求解速度模型mT2时，需要选择第一次反演的结果作为初始模型，我们选择后验样本的一个结果作为起始模型进行第二次MCMC反演.不同于第一次反演时的全采样方法，第二次反演时我们只对目标区域使用连续的吉布斯算法进行采样.为对比局部采样的反演效果，我们同时设置了一组模型全采样的数据进行对比，具体结果如图8所示.

图8a显示了使用全采样的扩展Metropolis算法采样后验概率密度函数得到的五个速度模型，用图8a的后验模型与第一次反演得到的初始模型相减，得到扰动变化如图8b所示.图8c是用局部采样的MCMC反演得到的后验分布，图8d是用图8c与初始反演模型相减的结果.对比图8a、c和模型mT2，可以看出图8a、c在浅层位置都反演出了一定的高速分布，但是图8a浅层高速分布的位置范围变化较大，高速位置分布随机并不集中在目标区域，图8c则主要集中在目标区域位置.用图8b、d对比更加明显，全采样的反演相对初始模型的变化位置，除浅层外，深层也有变化.

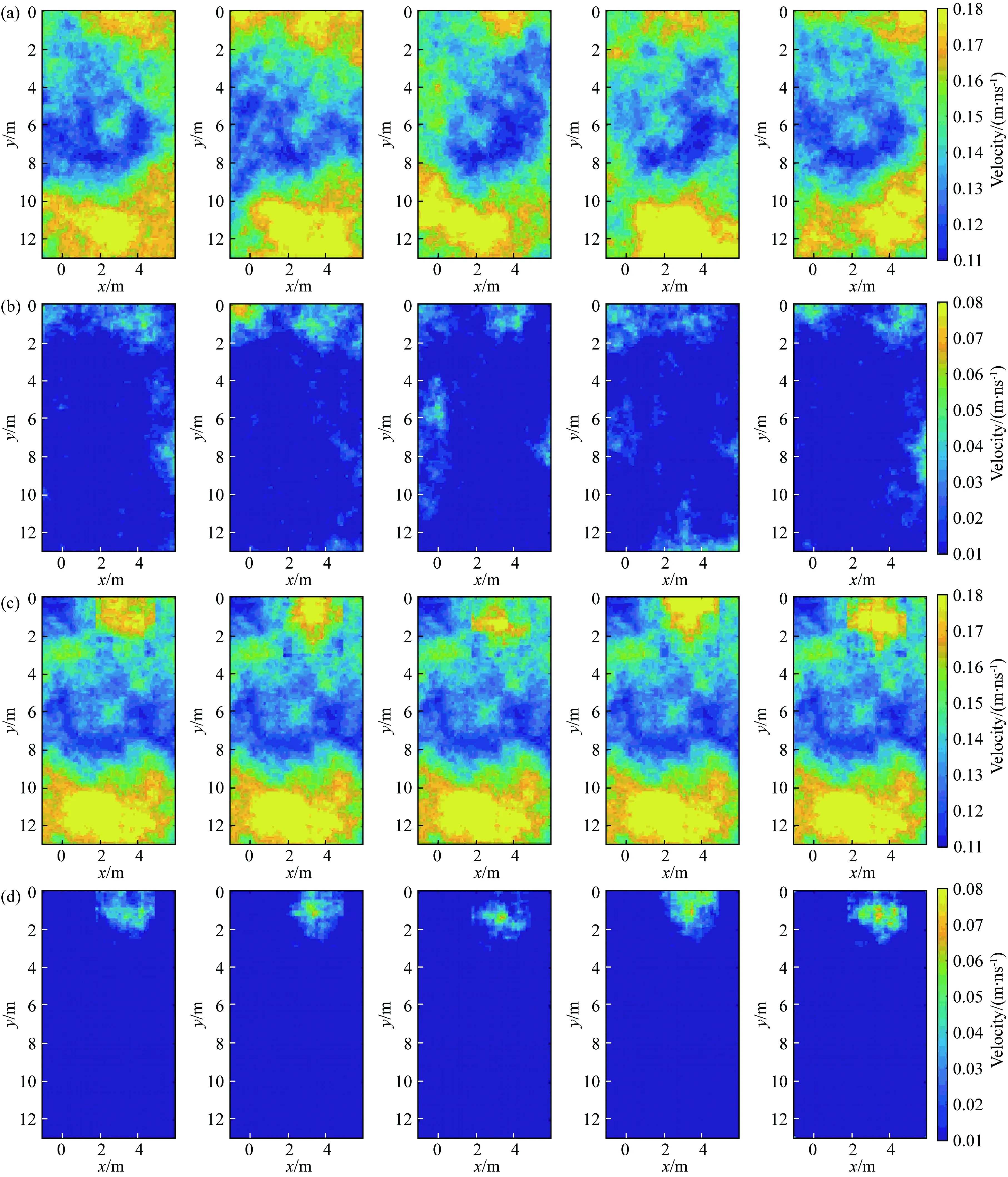
图8 (a)T2时刻全采样反演结果；(b)全采样扰动变化；(c)T2时刻局部采样反演结果；(d)局部采样扰动变化Fig.8 (a)Full sampling inversion model of T2;(b)The perturbation of the inversion;(c)Local sampling inversion model of T2;(d)The perturbation of the local sampling inversion

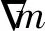
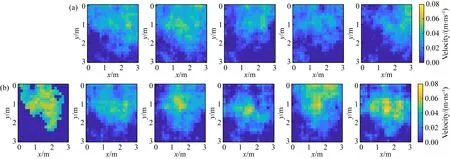
图9 (a)全采样法的目标区域反演结果；(b)局部采样法的目标区域反演结果Fig.9 (a)Target area of all sampling method;(b)Target area of local sampling method

图10a为设计的扰动的数值分布，图10b为相应位置全采样方法得到的数值分布，图10c为局部采样数值分布.明显看出图10c的数值分布与图10a更为接近.经过计算图10b的均值为1.8×10-2m·ns-1，图10c的均值为3.1×10-2m·ns-1，更接近扰动位置设计的均值4.5×10-2m·ns-1，证明了局部采样MCMC方法的有效性.

4 结论

(1)本文针对时移反演问题，提出了一种基于MCMC方法求解的通用框架，将MCMC算法与双差法相结合，对时移的目标位置进行有效的反演.MCMC反演采用扩展Metropolis算法结合连续吉布斯采样求解，双差法反演时将第一次反演的结果作为初始模型，并使用局部采样的方式，减小了计算量，提高了目标区域的求解效率.

图直方图分布；(b)全采样目标位置直方图分布；(c)局部采样目标位置直方图分布Fig.10 (a) histogram;(b)All sampling histogram;(c)Local sampling histogram

(2)使用局部采样的MCMC方法只对目标区域进行采样，即连续吉布斯采样法范围限定为时移目标区域，减小了非目标区域的影响，使目标区域反演结果更加准确.具体在时移反演时，对比了全采样的MCMC方法和局部采样的MCMC方法，分析了两者时移反演结果的误差，证明了局部采样的MCMC反演对目标区域的反演误差更小，准确度更高.

(3)将MCMC方法应用到GPR数据时移反演中，通过对GPR的模拟数据进行反演，理论模型和反演结果基本符合，有效的反演出探地雷达数据的时移扰动，准确的反映了地下介质不同时间内的速度变化，说明了MCMC反演方法的有效性和可靠性.