瞬变电磁虚拟波场二阶Born近似成像算法

樊亚楠，李貅*，戚志鹏，鲁凯亮

1 长安大学地质工程与测绘学院，西安 710054 2 长安大学地球物理场多参数综合模拟实验室(中国地球物理学会重点实验室)，西安 710054

0 引言

瞬变电磁法采集的信号为异常体引起的纯二次场，具有成本低、装置轻便、工作效率高等优势，因而被广泛应用于地下水探测(Fitterman and Stewart，1986；Foley et al.，2016)、金属矿勘探(Nabighian and Asten，2002；Vallée et al.，2011；底青云等，2019)、含水采空区探测(Li D S et al.，2019)以及隧道超前预报(Li Y et al.，2019；Liu et al.，2020)等领域中(孙怀凤等，2021).然而，瞬变电磁场满足时间域扩散方程，刻画的是电磁场的感应扩散特征，不易于对电性界面成像(李貅等，2010，2012)，而波动场满足波动方程，反映的是波的传播特性，易于对地质界面成像(薛国强等，2006).因此，通过波场反变换将瞬变电磁场转换为虚拟波场，即可借助地震勘探中成熟的成像方法进行瞬变电磁拟地震成像(薛国强等，2011；戚志鹏等，2013；Xue et al.，2013,2019；钟华森等，2016).

在地震勘探中，Born近似算法可以解决积分方程解非线性的问题(Cohen and Bleistein，1977，1979；黄联捷和杨文采，1991)，在无初始速度模型的条件下，可以直接得到深度剖面，克服了偏移算法需要事先给定初始速度模型的缺陷(丁科和宋守根，2004)，因此，该方法被广泛应用于地震勘探成像领域.Cohen和Bleistein(1979)、Bleistein和Cohen(1982)、Bleistein等(2001)假定反射波足够弱，针对地震反演中的二维速度变化问题将非线性问题进行线性化处理，率先建立了Born近似逆散射理论.Beylkin(1984)利用Born近似小扰动理论，将反演问题线性化，引入傅里叶算子求解第一类Fredholm积分方程.Beylkin和Burridge(1990)提出了基于单散射的逆散射算法，进一步验证了Born近似算法在对地震数据进行线性化时所起的重要作用；黄联捷和杨文采(1991)推导出了2.5维声波方程的逆散射表达式，利用傅里叶变换快速获得速度扰动量，使Born近似算法的适用性得以提高.丁科和宋守根(2004)利用逆散射序列对含有地震多次波信息的数据进行奇性界面反演，使该方法不仅适用于小扰动量介质模型的反演，而且对于大扰动量地质模型同样适用；Beylkin(1985)、Mao等(2013)、Ouyang等(2015)提出了二阶Born近似的非线性反演算法，克服了一阶Born近似仅适用于弱散射介质的局限性.

在电法勘探领域，樊亚楠等(2019)在波场反变换基础上，利用Born近似成像算法实现了对地质界面快速成像的目的.由于Born近似算法在弱散射条件下，忽略散射场使方程线性化，导致对大扰动量的成像会产生较大的误差.因此本文在波场反变换的基础上，借鉴地震勘探上的二阶Born近似算法进行拟地震成像研究，使得在强散射介质中能够准确定位地质界面的位置和形态.

本文基于波场反变换，将波动方程中的总波场和总波速分为两部分，并运用Green定理推导出了一维常背景速度地质模型的Born近似表达式，然后考虑散射序列二阶项对成像结果的影响，根据递推公式，推导出了适用于大扰动量模型的二阶Born近似成像算法.通过对三层、四层模型的解析解以及二维、三维模型的计算可知，Born近似算法对地下电性界面成像结果较差，而二阶Born近似算法能够较为准确地定位地质界面的位置和形态.因此，建立在波场反变换基础上的二阶Born近似成像算法可以实现对大扰动地质模型界面的准确定位和快速成像.

1 基本原理

1.1 Born近似算法

由文献(Lee et al.，1989)可知，瞬变电磁扩散场与虚拟波动场之间的关系式为

(1)

其中Hz(r,t)表示磁场强度的z分量，单位为A·m-1，其满足的扩散方程为

(2)

U(r,τ)表示虚拟波场，其满足的时间域波动方程为

(3)

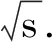
虚拟波场满足的波动方程在频率域的表达式可以写为

(4)

为确保波动方程在无边界介质中解的唯一性，防止波从无穷远处向源点传播，设方程(4)满足如下的索莫非辐射边界条件：

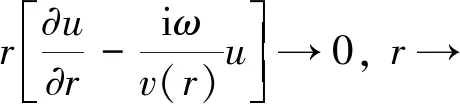
(5)

根据扰动理论，可将地下变化的波速分为两部分：全局性大尺度缓慢连续变化的背景波速v0(r)和局部快速变化的扰动速度α(r)，为了保持与波动方程形式相一致，可以将两者关系表示为如下的形式：

(6)

同时，缓慢连续变化的背景波速v0(r)不产生新的震相，只与入射波场有关，将这部分波场记为背景波场ui(r,rs,ω)；局部快速变化的波速扰动产生新的震相，与入射波场和扰动波速有关，把入射波、绕射波和随机散射波统称为散射波场，记为us(r,rs,ω)，因此

u(r,rs,ω)=ui(r,rs,ω)+us(r,rs,ω).

(7)

将式(6)、(7)代入式(4)中，可以得到：

(8a)

+us(r,rs,ω)],(8b)

为求解方程(8b)，引入Green函数G(r,rg,ω)，其满足方程：

(9)

运用Green定理，经过一系列推导可得：

+us(r,rs,ω)]d3r.

(10)

由式(10)可知，界面速度扰动量α(r)和散射波场us(rg,rs,ω)之间存在非线性的关系，要准确求解速度扰动量α(r)，必须对其进行线性化近似，考虑当扰动量较小时，即us(r,rs,ω)≪ui(r,rs,ω)，忽略右端项中的散射场us(r,rs,ω)，这时可以得到：

(11)

其中ui(r,rs,ω)=G(r,rs,ω)，因此：

(12)

式(12)即为虚拟波动场关于电性界面速度扰动量的Born近似表达式.

在一维背景速度为常数、零偏移距条件下，即v0(x)=v0=const，xs=xg，式(12)可以写为：

(13)

根据文献(Bleistein et al.，2001)可知，在一维常速度背景下Green函数的解析表达式为：

(14)

假定接收点位于地表，即x=0，并将式(14)代入式(13)中，可以得到：

(15)

根据Fourier变换对的表达式：

(16)

可以求得速度扰动量的表达式：

(17)

由(17)式可知，通过Fourier变换可以快速由虚拟波场的数据求得界面的速度扰动量.

根据图1阶跃函数以及图2 Delta函数的频谱图可知，阶跃函数的频谱主要集中在低频区域，而且随着频率的升高振幅逐渐减小，而Delta函数的频谱振幅始终等于1.图3、图4分别展示了全频带、缺少零频信息、10～100 Hz、10～40 Hz的阶跃函数以及Delta函数，黑色实线表示函数的真实值，黑色圆圈表示有限带宽的阶跃函数和Delta函数.随着带宽越来越窄，阶跃函数变形越来越严重，而Delta函数几乎不受频带的影响，因此可知有限带宽的Delta函数比有限带宽的阶跃函数更容易识别电性界面.

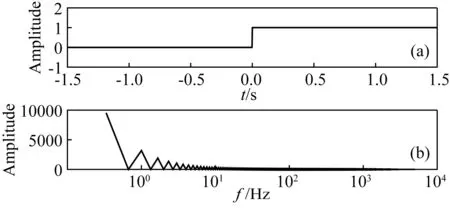
图1 阶跃函数及其频谱图(a)阶跃函数；(b)阶跃函数的频谱图.Fig.1 Step function and its spectrum(a)Step function;(b)Spectrum diagram of step function.

图2 Delta函数及其频谱图(a)Delta函数；(b)Delta函数的频谱图.Fig.2 Delta function and its spectrum(a)Delta function;(b)Spectrum diagram of Delta function.

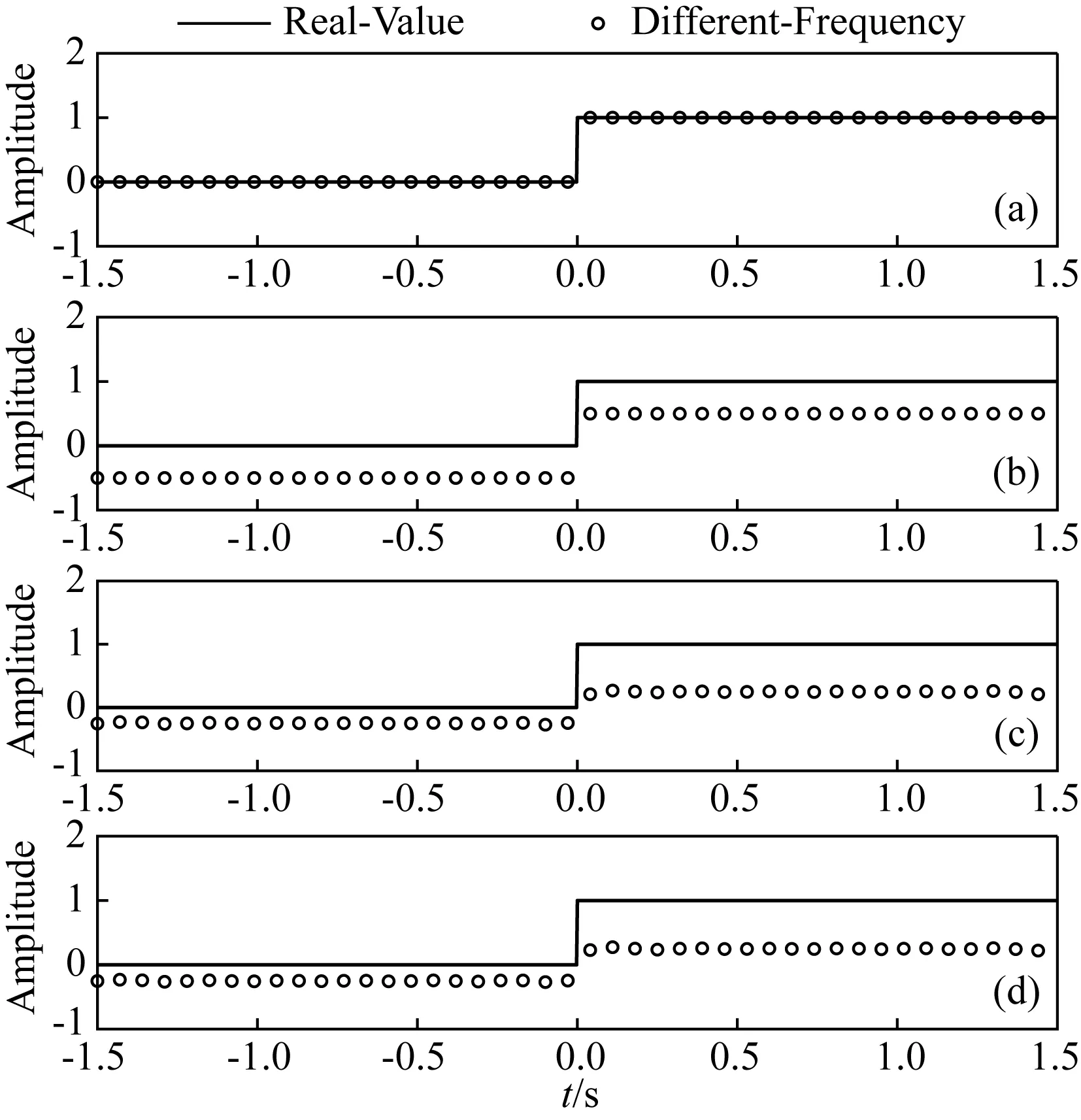
图3 不同频率的阶跃函数(a)全频带；(b)缺少0频信息；(c)10～100 Hz；(d)10～40 Hz.Fig.3 Step functions of different frequencies(a)Full frequency band;(b)Lack of 0 frequency information;(c)10 to 100 Hz;(d)10 to 40 Hz.

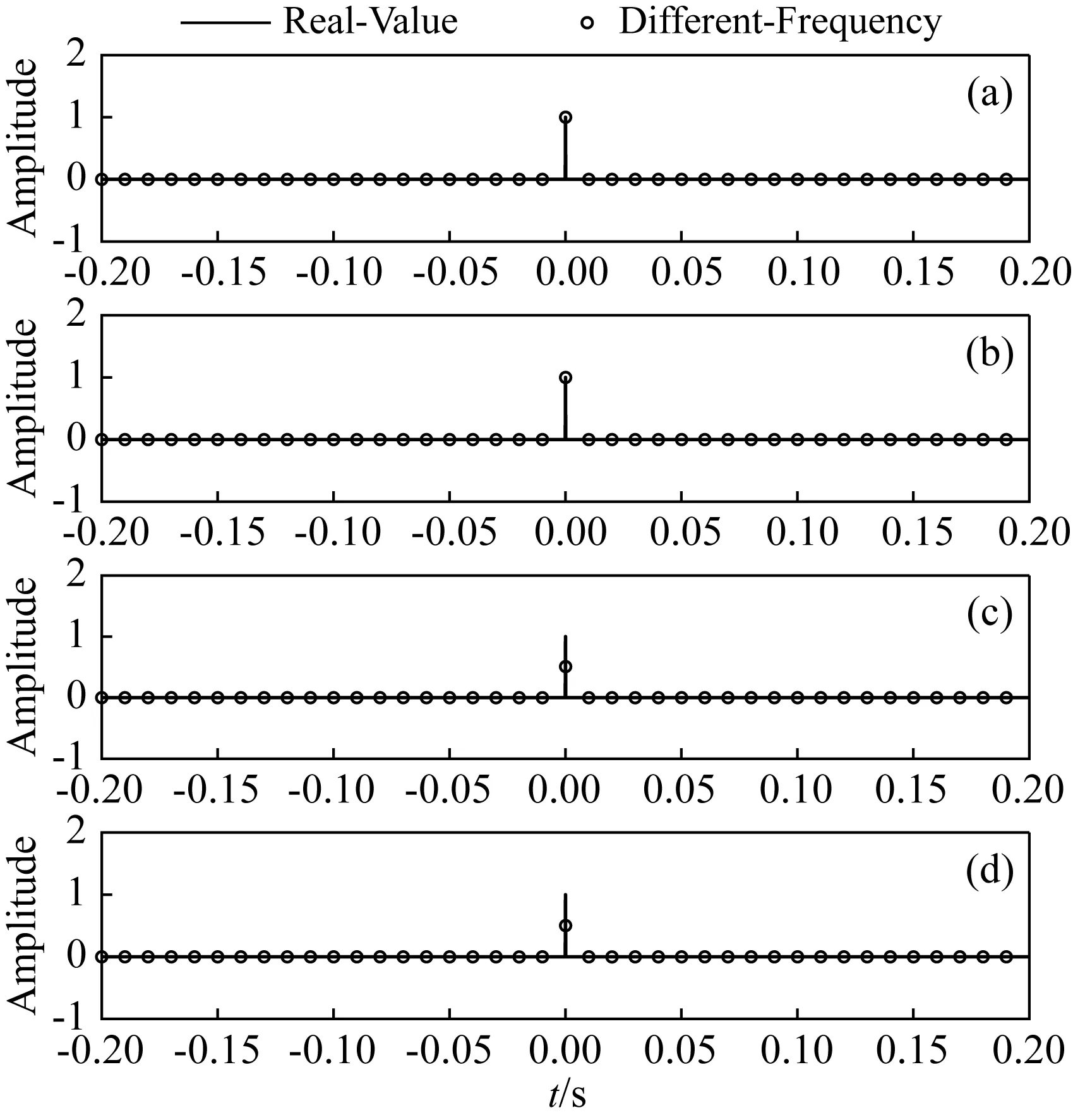
图4 不同频率的Delta函数(a)全频带；(b)缺少0频信息；(c)10～100 Hz；(d)10～40 Hz.Fig.4 Delta functions of different frequencies(a)Full frequency band;(b)Lack of 0 frequency information;(c)10 to 100Hz;(d)10 to 40 Hz.

由于瞬变电磁拟地震成像仅需要定位电性界面的位置，因此，本文使用Delta函数形式的反射率函数识别电性界面，记为β(x)，通过对速度扰动量函数α(x)求一阶导数，即可得到界面反射率函数的表达式：

(18)

1.2 二阶Born近似算法

已知Born近似算法忽略散射场，虽然使积分方程线性化，但是由于其只利用了散射序列中的第一项，丢失了部分有效信息，只适用于小扰动量介质的成像(丁科和宋守根，2004).因此，本文将对散射序列中的各项进行分析研究.

已知波动方程(4)的解具有如下的形式：

×u(r,rs,k)d3r,(19)

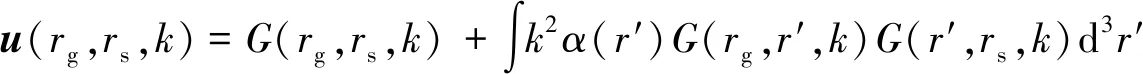
=u0+u1+u2+…

(20)

式(20)称为散射序列或Born序列.已知u(r,rs,ω)=ui(r,rs,ω)+us(r,rs,ω)，因此散射场的表达式为：

=u1+u2+…

(21)

根据(21)式可知，去掉第二项以后，即为Born近似的表达式，同时在(21)式中存在如下的递推关系：

(22)

对式(21)取前两项，可得：

×G(r′,r″,k)u(r″,rs,k)d3r″d3r′.

(23)

当偏移距为零时，即xs=xg=0，则Green函数的表达式为：

(24)

将式(24)代入式(23)中，可以得到：

×u(r″,0,k)dx″dx′.

(25)

已知Green函数的另一种表达形式为：

(26)

将式(26)代入式(25)，整理可得下面的方程组：

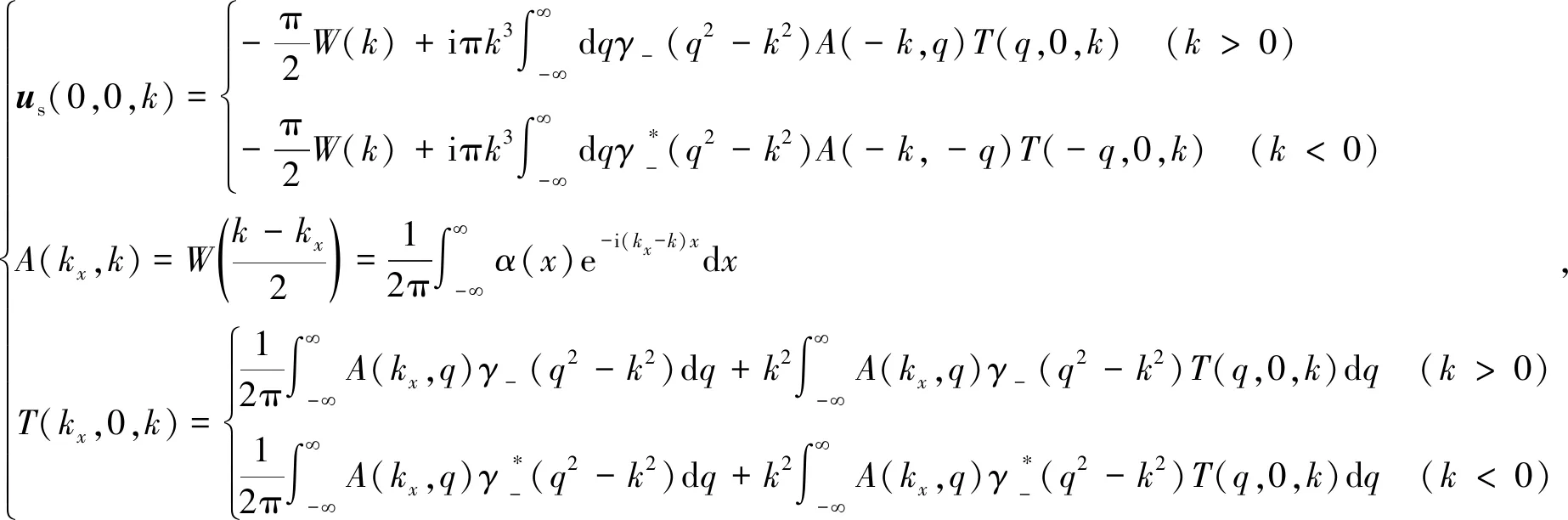
(27)

由式(27)可知，各变量之间存在循环迭代的关系.令us(0,0,k)=εus(0,0,k)，则式(27)可写为：

(28)

当n=1时，可得：

(29)

当n=2时，可得：

(30)

当n=3时，可得：

(31)

通过循环迭代依次可以求得W(k)、A(kx,k)和T(kx,0,k)，从而得到二阶Born近似反射率函数β(x)的表达式：

(32)

2 算法验证

2.1 电阻率变化对结果的影响

本节主要探究电阻率变化对Born近似算法以及二阶Born近似算法结果的影响，设置了H、K型模型，电性界面距地面分别为100 m、200 m，保持第一层与第三层的电阻率值不变，使模型第二层的电阻率依次变化.H型模型第一层与第三层的电阻率均设置为100 Ωm，设置第二层电阻率与背景电阻率的差异越来越大，依次为90 Ωm、80 Ωm、70 Ωm、60 Ωm；K型模型第一层与第三层的电阻率均设置为10 Ωm，第二层电阻率依次设置为20 Ωm、30 Ωm、40 Ωm、50 Ωm.模型示意图如图5所示，均选择第一层作为背景速度v0，分别计算了Born近似算法和二阶Born近似算法的结果，如图6，7所示.

图5 三层模型示意图(a)H型模型；(b)K型模型.Fig.5 Three-layer model diagram(a)H-type model;(b)K-type model.

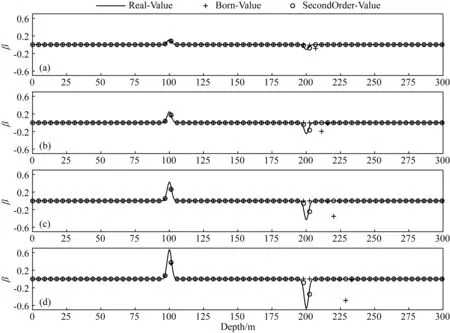
图6 H型模型Born近似、二阶Born近似以及真实值结果图(a)ρ1=100 Ωm，ρ2=90 Ωm，ρ3=100 Ωm；(b)ρ1=100 Ωm，ρ2=80 Ωm，ρ3=100 Ωm；(c)ρ1=100 Ωm，ρ2=70 Ωm，ρ3=100 Ωm；(d)ρ1=100 Ωm，ρ2=60 Ωm，ρ3=100 Ωm.Fig.6 Born approximation,second-order Born approximation and real value of H-type model

图中，黑色实线、黑色加号、黑色圆圈分别表示三层模型电性界面反射率函数的真实值、Born近似值、二阶Born近似值，其幅值表示电性界面反射率函数的大小.从H型模型的结果图中可知，黑色加号与黑色实线仅在第一个电性界面处重合，随着中间层与背景电阻率的差异变大，两者所指示的第二个电性界面的位置差也越来越大，K型模型结果类似.说明了Born近似算法仅能正确定位第一个电性界面的位置，随着电阻率差异变大，对第二个电性界面的定位偏差也会变大，这是由于在第一个电性界面处，第一层真实的速度与背景速度是一致的，因此对于第一个电性界面能够正确反映；对于第二个电性界面，由于第二层的速度与背景速度是不一致的，因此会造成一定的误差.反观黑色圆圈与黑色实线在两个电性界面处几乎重合，说明了二阶Born近似算法可以较好地反映地下电性界面的位置，其结果与真实值的偏差几乎不会随着电阻率差异变大而变大.以上分析说明了Born近似算法仅适用于小扰动量的成像问题，对于大扰动量模型，几乎不能正确定位界面的位置；而二阶Born近似算法几乎不受电阻率变化的影响，在大扰动量模型中具有一定的优越性.

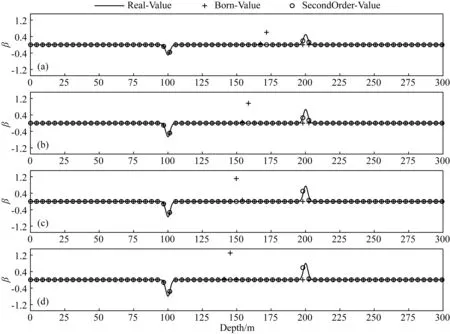
图7 K型模型Born近似、二阶Born近似以及真实值结果图(a)ρ1=10 Ωm，ρ2=20 Ωm，ρ3=10 Ωm；(b)ρ1=10 Ωm，ρ2=30 Ωm，ρ3=10 Ωm；(c)ρ1=10 Ωm，ρ2=40 Ωm，ρ3=10 Ωm；(d)ρ1=10 Ωm，ρ2=50 Ωm，ρ3=10 Ωm.Fig.7 Born approximation,second-order Born approximation and real value of K-type model

2.2 层厚变化对结果的影响

本节主要探究模型层厚变化对结果的影响，设置了HK型模型，模型的四层电阻率分别设置为：100 Ωm、10 Ωm、100 Ωm、1 Ωm，模型示意图如图8所示，分别设置两组模型：第一组模型第一层、第三层厚度均设置为100 m，第二层厚度依次设置为40 m、30 m、20 m、10 m；第二组模型第一层厚度为100 m，第二层厚度为50 m，第三层层厚依次设置为40 m、30 m、20 m、10 m.在计算过程中，均将第一层作为背景速度，相关计算结果如图9，10所示.

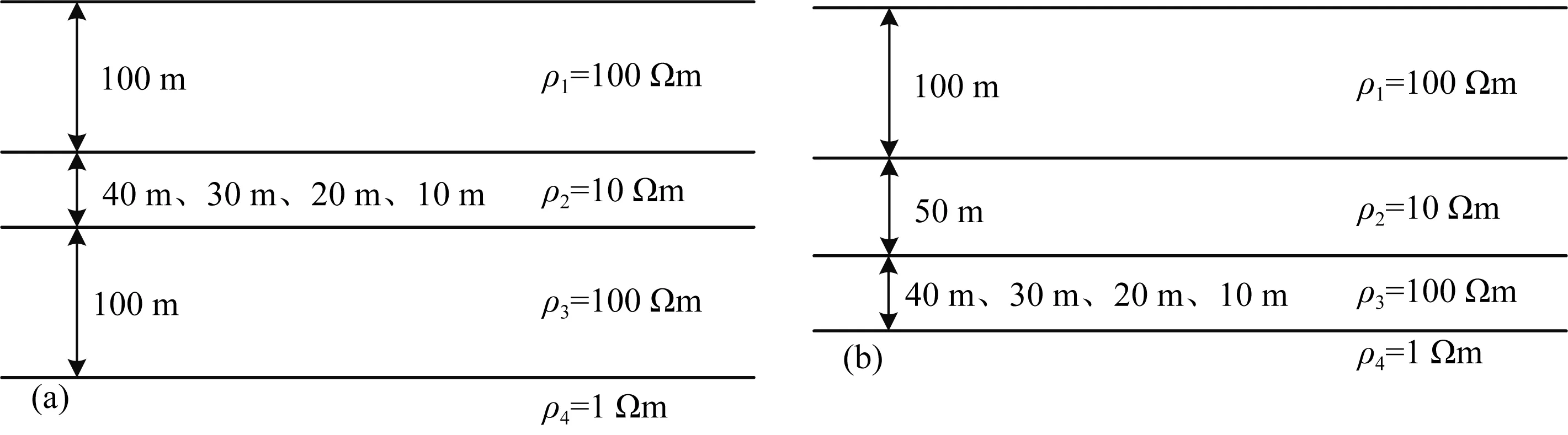
图8 四层HK型模型示意图(a)改变第二层厚度；(b)改变第三层厚度.Fig.8 The schematic diagram of the four-layer HK model(a)Changing the thickness of the second layer;(b)Changing the thickness of the third layer.

图9 改变第二层厚度的HK模型结果图(a)h1=100 m，h2=40 m，h3=100 m；(b)h1=100 m，h2=30 m，h3=100 m；(c)h1=100 m，h2=20 m，h3=100 m；(d)h1=100 m，h2=10 m，h3=100 m.Fig.9 Results of HK model with changing the second layer′s thickness

图中，黑色实线、黑色加号、黑色圆圈分别表示地下电性界面反射率函数的真实值、Born近似值、二阶Born近似值.根据两组模型的计算结果可知，各层电阻率不变、只改变第二层或者第三层厚度的情况下，黑色加号与黑色实线仅在第一个电性界面处重合，对于第二个、第三个电性界面，两者的偏差较大，说明Born近似算法在厚度不断变化的模型中除了第一个电性界面外，其余界面均不能正确定位；然而黑色圆圈与黑色实线几乎完全重合，不受模型层厚变化的影响，均能正确定位电性界面的具体位置，这进一步说明二阶Born近似算法相对比Born近似算法具有一定的优越性.

3 理论模型计算

3.1 二维模型

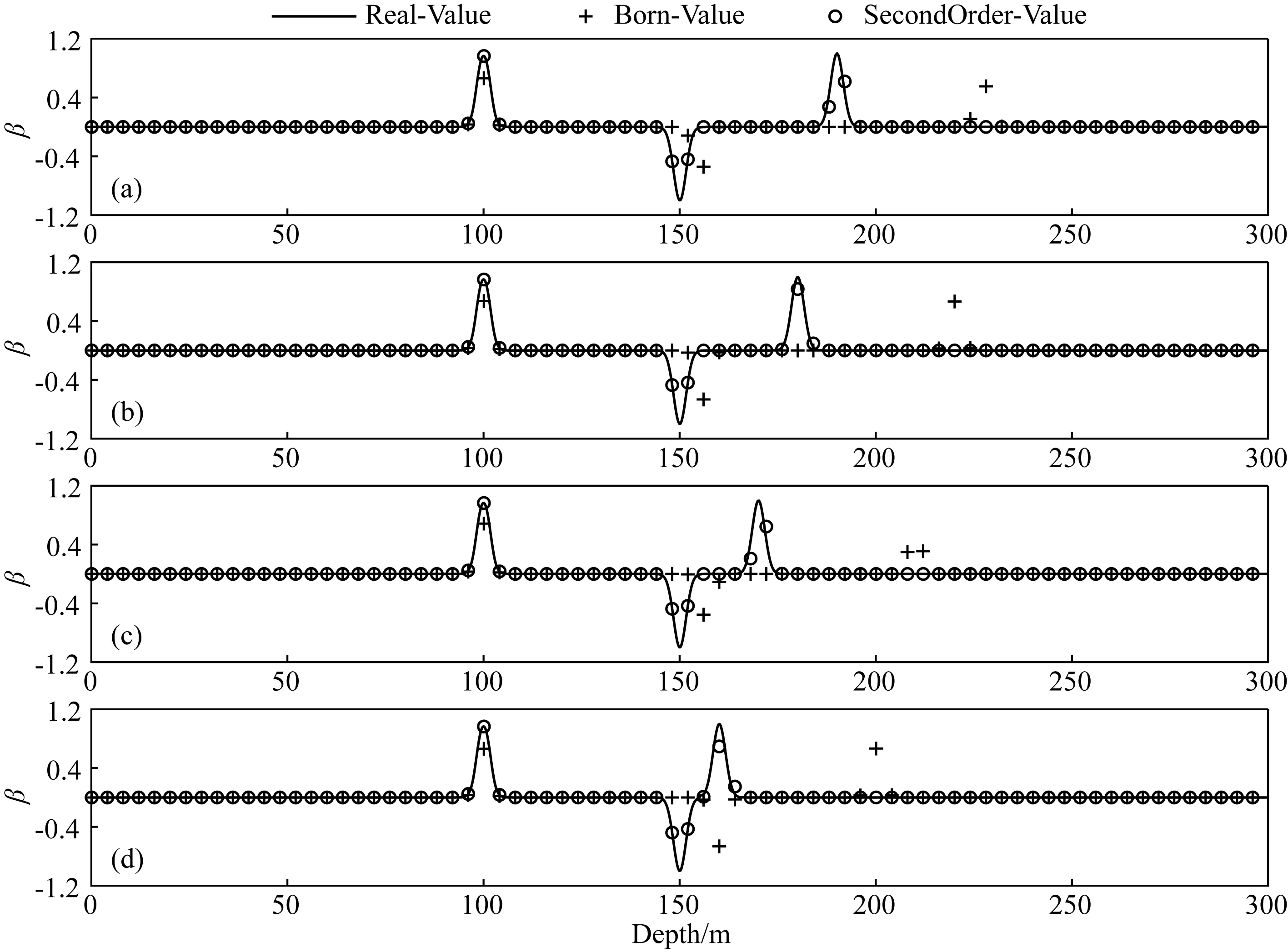
图10 改变第三层厚度的HK模型结果图(a)h1=100 m，h2=50 m，h3=40 m；(b)h1=100 m，h2=50 m，h3=30 m；(c)h1=100 m，h2=50 m，h3=20 m；(d)h1=100 m，h2=50 m，h3=10 m.Fig.10 Results of HK model with changing the third layer′s thickness

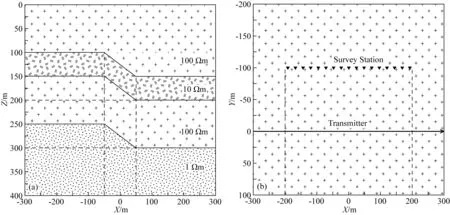
图11 二维模型示意图(a)XOZ平面；(b)XOY平面.Fig.11 Diagram of two-dimensional model(a)XOZ plane;(b)XOY plane.

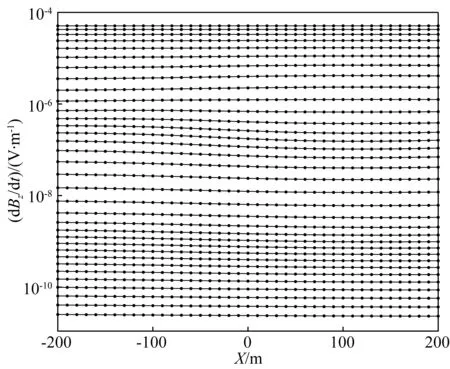
图12 二维模型的多测道图Fig.12 Multi-channel diagram of two-dimensional model

图13 二维模型的虚拟波场图Fig.13 Pseudo wave-field diagram of two-dimensional model

在成像的计算过程中将第一层作为背景速度，图14为二维模型的Born近似和二阶Born近似算法的成像结果图，虚线表示二维模型真实的地质界面位置，从图中可知两种算法均能反映出模型有三个电性界面.Born近似的结果仅能准确地定位第一个地质界面，上盘距地面大致100 m，下盘距地面大致150 m，第二个、第三个电性界面的成像结果与实际地质界面的位置分别大致相差30 m和40 m，而且断层的形态与真实模型有一定差距；二阶Born近似算法成像的结果对地下三个电性界面的位置定位准确，成像的结果与虚线几乎重合，横向上在X=-50～50 m处断层的形态较为明显，各界面的埋深与模型设置几乎是一致的.可见，相比于Born近似算法的成像结果，二阶Born近似算法的成像效果较好.

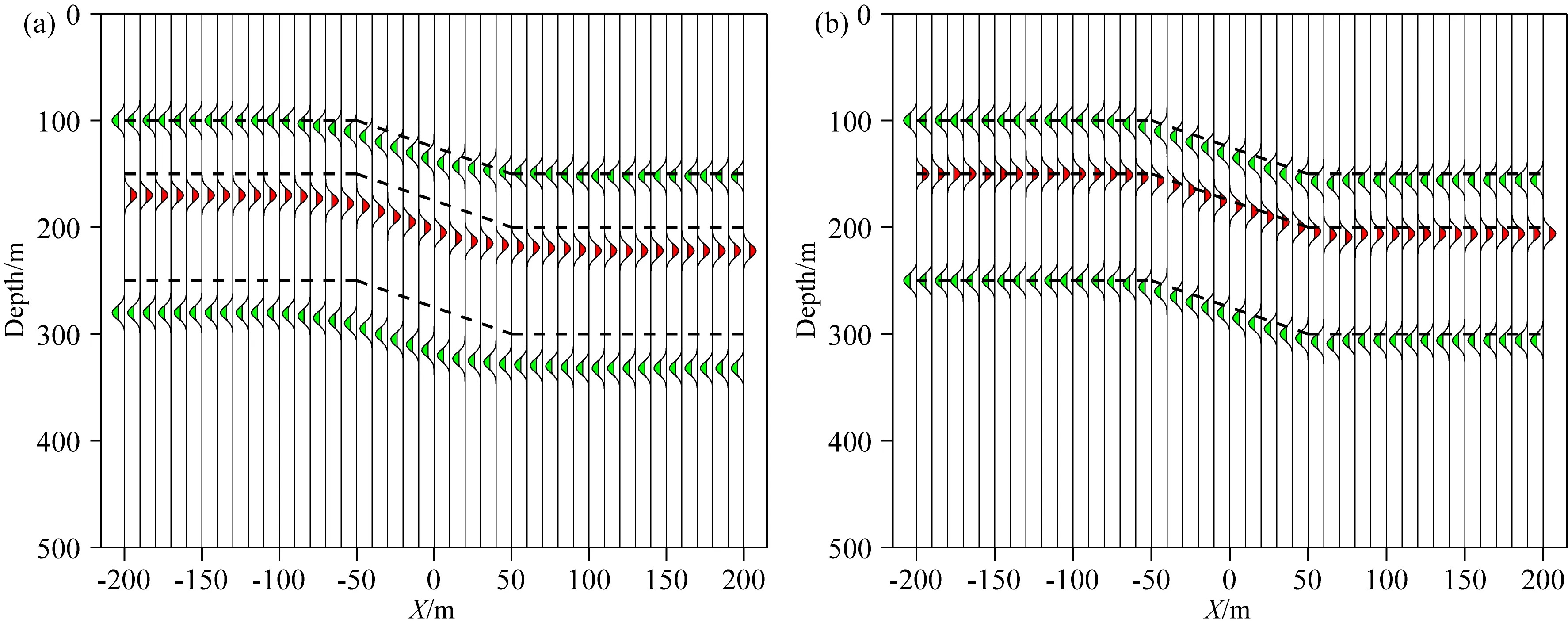
图14 二维模型的成像结果(a)Born近似结果；(b)二阶Born近似结果.Fig.14 Imaging results of the two-dimensional model(a)Born approximation results;(b)Second-order Born approximation results.

3.2 两个低阻薄板模型

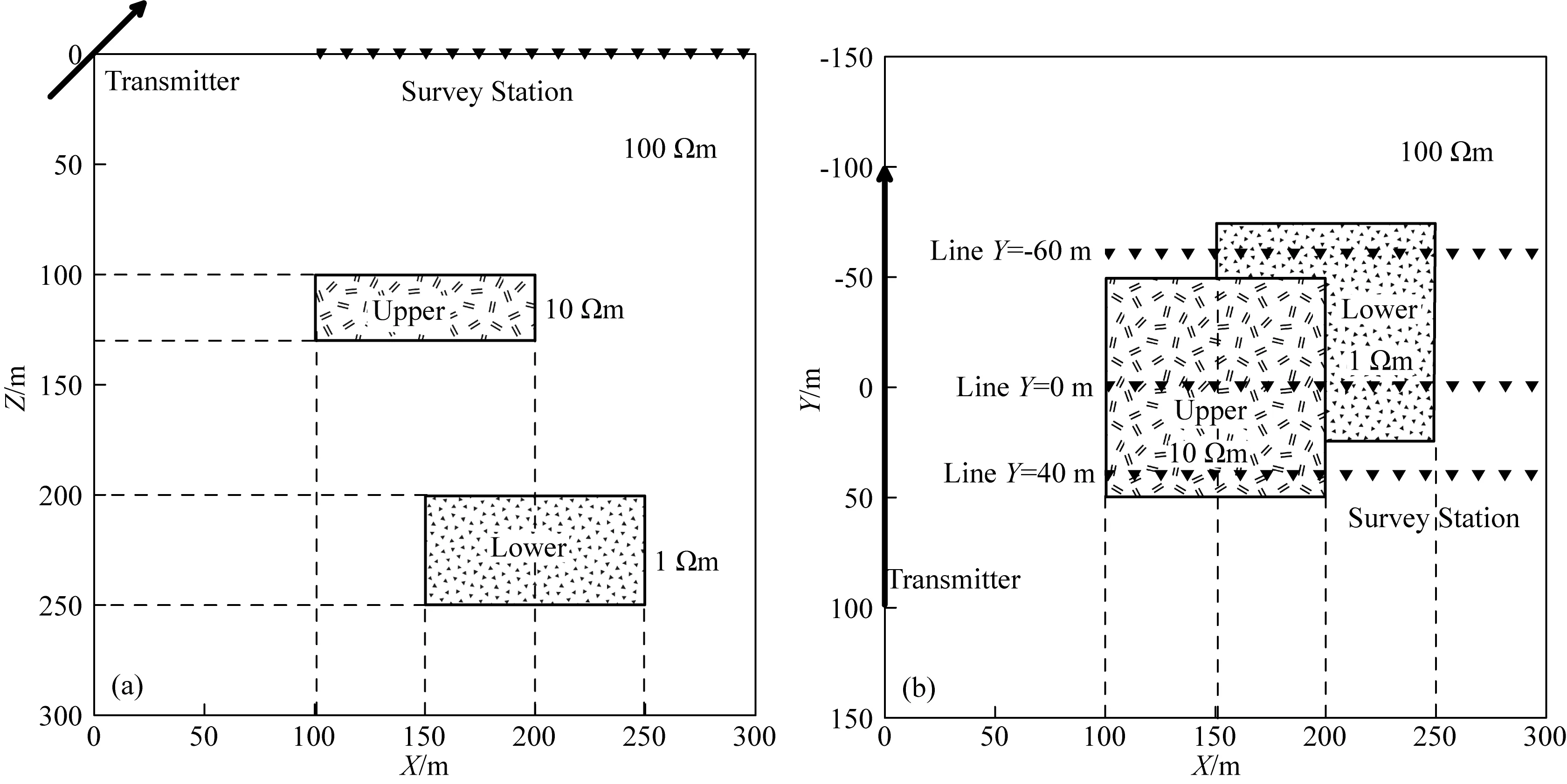
图15 两个低阻薄板模型示意图(a)XOZ平面；(b)XOY平面.Fig.15 Schematic diagram of two low-resistance thin plates(a)XOZ plane;(b)XOY plane.

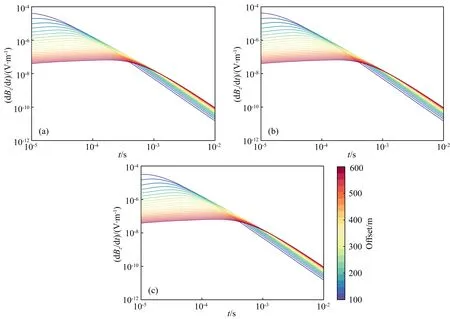
图16 三维模型的瞬变电磁数据(a)Y=40 m；(b)Y=0 m；(c)Y=-60 m.Fig.16 Transient electromagnetic data of three-dimensional model

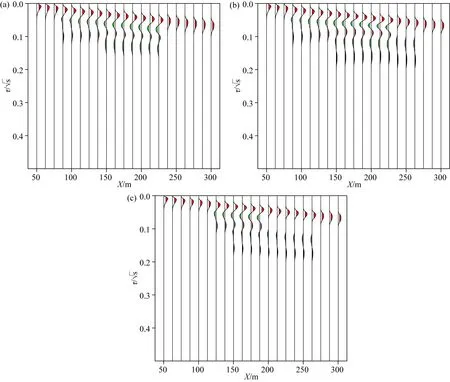
图17 三维模型的虚拟波场图(a)Y=40 m；(b)Y=0 m；(c)Y=-60 m.Fig.17 Pseudo wave-field diagram of three-dimensional model

图19 测线Y=0 m的成像结果(a)Born近似结果；(b)二阶Born近似结果.Fig.19 Imaging results of line Y=0 m(a)Born approximation results;(b)Second-order Born approximation results.

图20 测线Y=-60 m的成像结果(a)Born近似结果；(b)二阶Born近似结果.Fig.20 Imaging results of line Y=-60 m(a)Born approximation results;(b)Second-order Born approximation results.

在成像的计算过程中将背景电阻率作为背景速度，图18—20分别展示了测线Y=40 m、Y=0 m、Y=-60 m的Born近似算法以及二阶Born近似算法的拟地震成像结果图，其中黑色虚线表示该测线下方异常体的真实位置.测线Y=40 m处，Born近似算法与二阶Born近似算法均对上部异常体的上下界面以及下部异常体的上界面有所反映，但是Born近似算法的成像结果与真实界面的位置大约相差30～40 m，而且界面倾斜与真实模型形态相差较大；而二阶Born近似算法的结果能够准确定位界面的位置以及异常体的形态.测线Y=0 m的Born近似成像的结果不能准确定位界面的位置，尤其是下部异常体的界面与真实界面大约相差50 m；二阶Born近似拟地震的结果可以较好地定位两个异常体的界面位置，而且其形态与真实模型相一致.测线Y=-60 m的拟地震Born近似成像结果仅反映了上部异常体的部分界面信息以及下部异常体的界面位置，但结果与真实模型的界面位置存在一定的偏差，而二阶Born近似算法的结果对界面的位置以及异常体的形态均能够准确定位.测线Y=40 m虽然只穿过上部异常体、未穿过下部异常体，但是计算瞬变电磁扩散场时会受到下部异常体的影响，因此成像的结果中含有下部异常体的部分信息，同理可知测线Y=-60 m处虽只穿过下部异常体，但对上部异常体也有所反映.通过对三维低阻薄板模型不同位置的3条测线进行Born近似算法以及二阶Born近似算法成像的结果可知，二阶Born近似算法的结果既可以准确反映两个低阻薄板上下界面的位置，又可以精确反映界面的形态，因此该方法相对比Born近似算法具有较高的精度和界面识别能力.

4 结论

本文基于瞬变电磁波场反变换，在波动方程中将总波场、总速度分为关于背景和扰动量的项，然后运用Green定理求解波动方程，并引入Born近似算法将积分方程线性化，建立了虚拟波场与界面反射率函数之间的关系.通过分析散射序列以及递推关系，本文保留了散射序列的前两项，推导出了二阶Born近似算法的表达式.通过探究电阻率变化、层厚变化对Born近似算法以及二阶Born近似算法的影响，可知二阶Born近似算法几乎不受影响，均能准确定位界面位置；根据理论模型的成像结果可知，相对比Born近似算法，二阶Born算法既可以准确反映二维模型地质界面的位置和形态，又能定位三维模型中的两个低阻薄板的埋深以及相对位置.综上可知，在波场反变换的基础上，二阶Born近似算法可以实现瞬变电磁拟地震快速、准确成像的目的.

本文主要研究散射序列的前两项即二阶Born近似与Born近似算法的结果对比，在后面的研究中将对散射序列的更高阶项进行探究.

致谢我们特别向审稿人和编辑对本文提出的建设性意见表示感谢．