基于独立稀疏SAE的多风电场超短期功率预测

2022-03-15杨保华张远航

电力系统及其自动化学报 2022年2期

李丹，王奇，杨保华，张远航

（1.三峡大学电气与新能源学院，宜昌 443002；2.新能源微电网湖北省协同创新中心，宜昌 443002）

随着具有强随机性和波动性的风能在电源结构中的占比持续增长，电网安全与稳定运行面临严峻挑战[1]。对风电功率进行准确、全面和客观的预测，是电力系统规划、分析和决策的重要基础。风电功率预测通常分为短期预测与超短期预测[2]。其中，超短期预测对风电场未来15 min～4 h内的出力进行预测，其预测结果为电网实时调度提供基础数据。由于风电功率具有波动性和随机性，当预测时长超过4 h时预测误差将超过15%[3]，难以满足电网调度的要求，因此目前对风电功率的预测多以超短期预测为主。

当前，众多学者提出了多种确定和不确定性风电功率超短期预测方法。在确定性预测方面，当前研究一方面关注引起风电波动的主要因素，精细化计及气象动态过程[4]、风电机组内部特征或风电场状态[5]，从多模型细化建模方面改善预测精度；另一方面，聚焦风功率自身的时序和非线性特性，引入人工智能和数据挖掘技术，通过模态分解[6]、特征提取或长短期时序记忆[7]等手段提高预测精度和效率。在不确定性预测方面，多采用基于数据驱动的非参数概率预测方法避免人为假设的主观性[8]。这些方法为缓解大规模风电接入与系统稳定运行之间的矛盾，提高风能消纳能力，发挥了重要作用。

随着集中式、大规模开发成为我国风电产业未来发展的新趋势，一方面，受气象过程时间惯性和空间相似性的影响，大型风电基地中多座风电场之间存在复杂的时空相关性[9]；另一方面，伴随着云计算、泛在电力物联网、大数据等新兴信息技术的发展，风电数据也日益多样化、复杂化和精细化。利用海量风电数据信息，深度挖掘不同时空分布下风电数据的内在规律，成为改善风电预测精度一个新的重要手段[10]。目前，众多学者将卷积神经网络CNN（convolutional neural network）[11]，长短期记忆LSTM（long short-term memory）神经网络[12]以及堆叠自编码SAE（stacked autoencoder）神经网络[13]等深度学习技术应用于风电功率预测。例如，为有效处理短期风电功率预测过程中的多类型影响因素，文献[11]利用CNN局部感受野对输入数据畸变容忍能力高的优势，将历史数据通过CNN提取的特征作为预测模型输入，然后利用这些特征作为门控循环单元GRU（gated recurrent unit）的输入提高风电功率的预测精度；文献[12]采用具有时序数据长短期记忆能力的LSTM神经网络，结合随机搜索方法优选预测模型超参数，改善超短期风电功率预测精度；文献[13]则采用结构简洁、训练难度小、特征提取能力更强的SAE网络，进行风电功率的特征提取和预测。以上文献体现出深度学习在风电功率预测方面的优势，但它们多针对单个风电场功率开展预测。

相对于单风电场，多风电场超短期预测的难点在于，由于风电场数量和潜在影响因素多，预测模型的解释变量增多，变量间的时间及空间的关系也更加复杂。文献[14]采用径向基神经网络的非线性分位数回归建立了适用于区域多风电场的概率预测模型，但其解释变量众多，使得高维回归方程的参数估计计算负担增加；文献[15]提出了一种对多风电场总出力的波动过程进行智能识别和波动规律挖掘的预测方法，来获取未来风电功率4 h的变化趋势，但该文献没有考虑多风电场之间的空间相关性；文献[16]将L1正则化加入到深度稀疏自编码器中获得新气象数据的稀疏特征，再对高维数据进行特征降维，消除指标间的多重共线性，实现高维数据向低维空间的压缩编码，但该方法并未对提取特征之间的独立性进行检验；文献[17]运用核主成分分析KPCA（kernel principal component analysis）法，对风电历史功率数据进行数据降维，提取多维风电数据的非线性特征，但对非线性降维后低维空间数据如何还原到实际高维空间的重构难题仍有待解决。同时，上述文献缺乏多风电场风电出力特征与神经网络结构之间关系的研究，神经网络模型的可解释性不足。

针对上述研究所存在的问题，本文将多风电场功率特点与深度学习思想相结合，提出一种基于独立稀疏堆叠自编码器ISSAE（independent sparse stacked autoencoder）的多风电场超短期功率预测方法。该方法基于一种独特的降维编码-特征预测-重构解码的预测框架，实现多风电场功率特征提取、潜在影响因素降维与特征优选、功率特征独立预测和重构还原的有机统一，有效化解非线性降维方法所面临的重构困难的问题。在SAE的多级编码器设计中，通过稀疏性激活神经元的学习能力，充分解析多维风电功率间的非线性关系；通过在损失函数中加入独立性约束惩罚项，消除低维风电特征的相关性，实现多风电场功率特征的独立并行预测；并通过在解码层中引入限制性激活函数使预测过程中超范围的数值回归允许范围，保证重构结果的合理性。某地区18座风电场的实际算例从预测精度及预测效率两方面验证了所提方法的有效性。

1 基于堆叠自编码器的多风电场超短期功率预测框架

1.1 自编码器AE

自编码器AE（autoencoder）是一个由输入层、隐含层和输出层组成具有结构对称性的无监督学习神经网络[18]，其典型结构如图1所示，包括编码过程和解码过程。

图1 自编码器结构Fig.1 Structure of AE

式中：F为隐含层输出的特征向量；f（·）与g（·）分别为编码与解码的激活函数；θ为网络参数，θ=[W1,W2,b1,b2]，表示编码和解码过程中的权重和偏置参数集合；N为训练样本个数；L为均方误差损失函数。

1.2 堆叠自编码器SAE

SAE是由2个或多个AE堆叠而成的深度神经网络，上一层编码器隐含层的输出作为下一层编码器的输入[19]，其结构如图2所示。

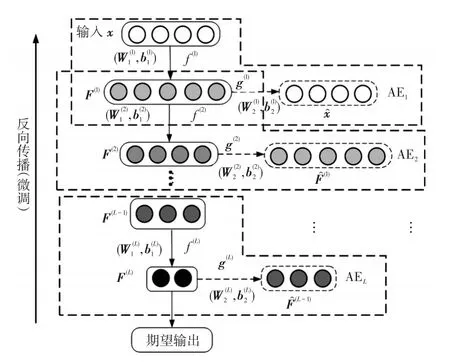
图2 堆叠自编码器结构Fig.2 Structure of SAE

SAE通过逐层编码，提取数据的深层特征，在处理具有复杂非线性相关性的高维数据时，比只有单隐含层的AE具有更强的特征提取能力[20]。

为避免多层神经网络训练时梯度弥散，SAE通常采用贪婪训练法将训练过程分为预训练和微调两阶段。预训练按照AE1到AEL的顺序进行，上一层AEL通过前向传播计算网络最佳参数W(L)、b(L)以及获得隐含层特征F(L)，再以F(L)作为下一层AEL+1的输入，训练得到 W(L+1)、b(L+1)和 F(L+1)，依次向下，推进直到训练结束。最后，全部L个AE被堆叠为SAE，根据最深层编码器输出与期望输出之间的误差，进行有监督训练，完成整体网络参数的微调。

1.3 双层ISSAE多风电场短期功率预测框架

为保证多风电场功率特征的独立性和重构结果的合理性，本文在SAE编码器设计中，引入稀疏化、独立性和约束性技术，建立如图3所示的双层ISSAE多风电场短期功率预测框架。图中，隐含层上标代表编码器序号，下标代表变量序号。整个多风电场短期功率预测模型自上而下分为降维编码、特征预测和重构解码3个阶段。

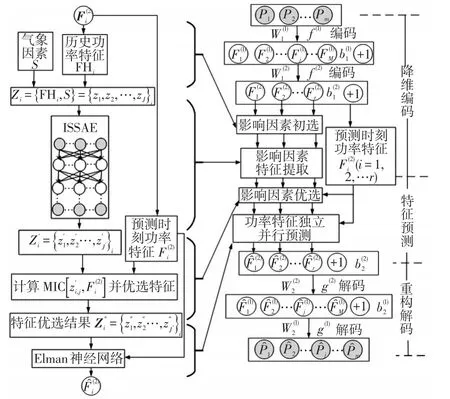
图3 降维-预测-重构的预测框架Fig.3 Prediction framework of dimensionality reductionprediction-reconstruction

1.3.1 特征预测阶段

特征预测嵌入到ISSAE的降维编码和重构解码之间。对原始多风电场功率数据降维编码后，将降维编码的低维独立特征作为预测对象进行预测，然后将特征预测的结果重构解码，最终获得多维风功率的预测结果。

1.3.2 降维编码阶段

（1）功率独立特征提取。输入m座风电场N个时刻的历史功率观测样本集PN×m=[P1,P2,…Pm]N，通过双层ISSAEP，非线性映射到M（M＞＞m）高维空间的，再提取r维（r＜＜m）的独立特征。

（2）影响因素初选和提取。与风电功率类似，功率特征主要受历史值变化规律和风速等气象因素的影响。考虑到数量众多的潜在影响因素之间包含冗余信息，在建立预测模型之前，需要对影响因素进行初选和独立特征提取。

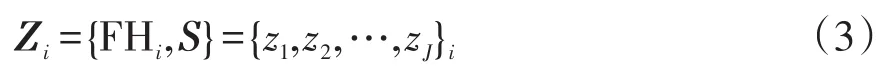
对初选输入Zi采用双层ISSAE网络提取J′维(J′≪ J)的低维独立特征，有

1.3.3 预测阶段

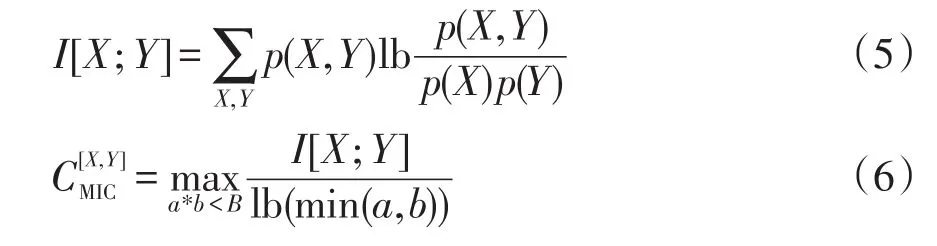
式中：I为互信息系数；p(X,Y)为变量X和Y的联合概率密度分布函数，p(X)和p(Y)分别为变量X和Y的边缘分布；a、b分别为在X,Y方向上划分网格的个数；a*b＜B表示在X和Y坐标上划分的网格总数小于B，B为变量，B一般取样本总量的0.6次方。

1.3.4 重构解码

利用ISSAEP训练得到的解码器将低维功率预测特征分两级解码重构，输出n个测试样本对应的m座风电场的功率预测结果

2 ISSAE的稀疏化、独立性和限制性技术

2.1 稀疏化技术

从数据降维角度看，对多维变量直接降维，不仅难以准确解析变量之间复杂的非线性关系，而且难以保证提取的低维特征之间相互独立。如果先映射到高维空间，使映射变量之间线性可分，可大大降低数据解析的难度。然而，当隐含层神经元数M大于或等于输入层神经元数m时，AE可能学习到恒等函数而失去特征提取能力。为此，对SAE中的升维编码器AE1采用稀疏化技术来抑制隐含层的神经元状态，既增加了编码算法鲁棒性，也可增强数据的线性可分性。

对sigmoid激活函数，当隐含层神经元输出近似为“1”时，认为该神经元被激活，否则为抑制状态。引入平均激活量，有

设定一个接近于0的常数ρ，在损失函数中引入Kullback-Leible散度惩罚项来保证不断逼近ρ，有

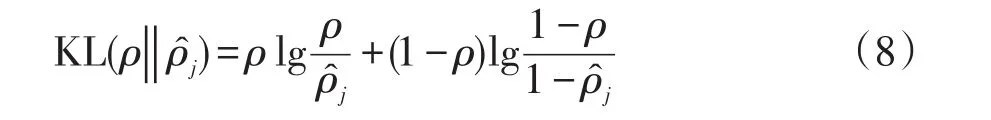
2.2 独立性技术

当AE1将原始多维变量非线性映射到高维线性空间后，在AE2中经过线性降维变换，即可得到指定维数r下的特征数据，实现降维。然而，对多风电场功率预测而言，除了需要降维减少预测变量和潜在影响因素数量以外，还需要消除提取特征之间的相关性，使各功率特征的独立预测成为可能。

本文采取以下两方面措施来保证提取特征之间的独立性。

（1）在AE2的编码过程中采用pureline线性激活函数，并在预训练中引入PCA降维权重系数Vr×M作为权重的初始值。Vr×M由的协方差矩阵特征分解后提取特征值最大的r个特征向量组成。

（2）在SAE整体模型参数的微调训练损失函数中引入线性无关惩罚项，即

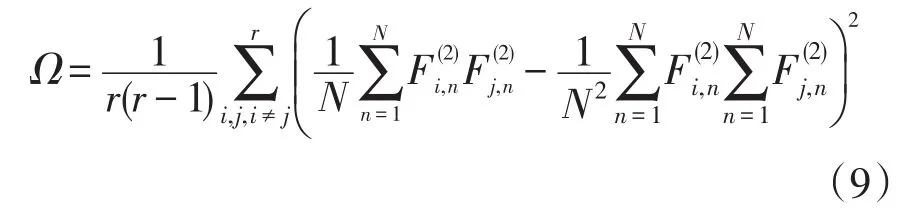
式中，Ω为不同维特征之间样本协方差的均方值，用来衡量不同维特征之间的总体线性相关程度。Ω=0代表降维特征之间线性无关；Ω越大，特征之间的线性相关性越强。

加入稀疏性及线性无关惩罚后的损失函数为

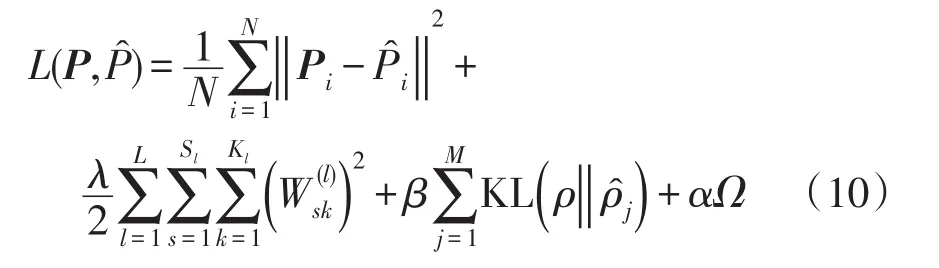
式中，λ、β、α分别为防止过拟合正则项、稀疏惩罚项和线性无关惩罚项的权重系数。

以上措施中，对AE2编码权重初始值的设定，保证了预训练过程从一个能较好保证特征独立性的初始参数出发，而在SAE的微调训练中通过线性无关惩罚进一步保证了训练过程始终向着特征线性无关的方向寻优。AE1编码结果的线性可分性与AE2编码结果的线性无关性相结合，共同保证了提取降维特征的独立性。

2.3 限制性约束

各座风电场功率均分布于[0,PNk](k∈[0,…,m])区间，其中PNk为第k座风电场的额定功率。为保证预测特征经过SAE解码得到的预测功率的合理性。在将各风电功率归一化到[-1，1]区间的前提下，在AE2中采用satlin饱和线性激活函数解码，其函数为

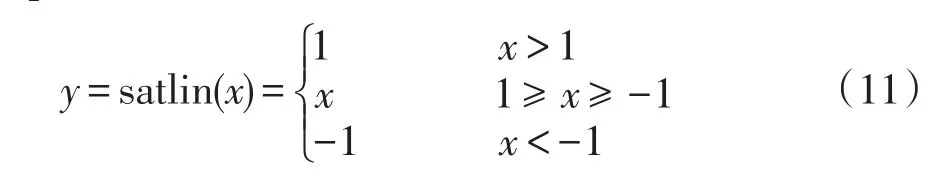
3 算例分析

3.1 算例简介

以某风电基地18座风电场的2016年小时级实测功率样本数据为分析对象，进行未来1 h的超短期功率预测，风电场之间距离5～382 km不等，单座风电场的装机容量在49.5～246 MW之间。图4为18座风电场全年8 760 h的总功率曲线。通过风电场的出力判断实际风资源季节性分布情况，将6—10月份划分为少风季，其余月份划分为多风季，分别进行预测分析。两组样本分别分为3部分：前90%样本中，随机选择80%作为训练集，剩下10%样本作为验证集对超参数寻优；最后10%样本作为测试集。

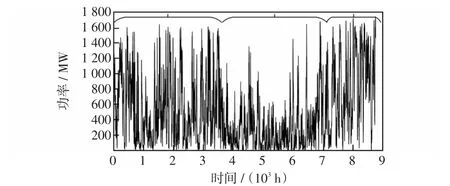
图4 2016年小时级总功率变化曲线Fig.4 Changing curve of hourly total power in 2016

从预测精度与效率两方面验证所提方法的应用效果，将ISSAE-Elman模型与不降维直接预测的Elman模型，以及AE、SAE和PCA等常用降维方法与Elman网络结合后的预测模型进行对比，分析稀疏化、独立性和限制性技术对降维特征独立性和降维结果合理性的改善作用。所有程序用Matlab2019a编写，在Intel（R）Core（TM）i7 CPU@2.30GHz计算机运行，预测结果取20次实验的平均值。

表1给出了降维-预测-重构模型的参数设置。风电功率特征维数的选择首先应满足降维后数据信息保留率大于90%的要求，按此原则提取的功率特征维数r≥ 5。然后经过验证集对r∈{5，6，…，18}进行寻优，确定r=7，此时降维后信息保留率为94.7%。潜在影响因素初选为预测时刻前6 h、前3 d相同时刻的历史特征值和预测时刻的气象信息（风电场群所在3个子区预测时刻最低和最高气温、天气类型和平均风速）组成的21维输入变量（J=21），优选后的强影响因素特征数J″=11。

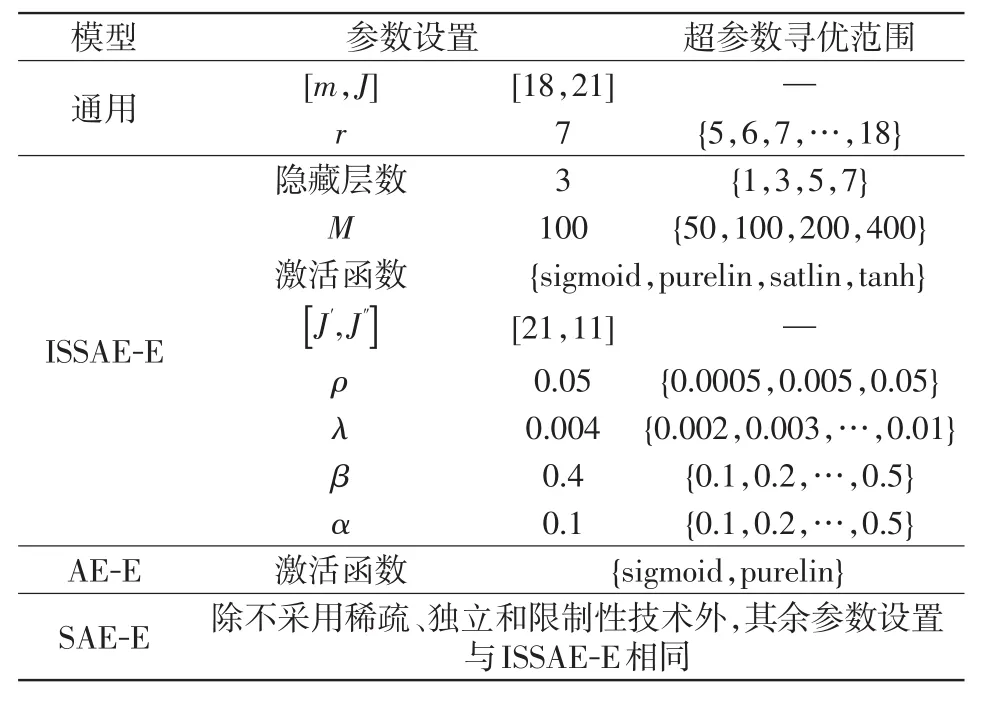
表1 模型的参数设置Tab.1 Parameter setting of models

3.2 不同预测模型预测结果的对比

表2分别给出了多风季与少风季5种模型对18座风电场功率预测结果的误差统计和预测时间。图5为两季各风电场预测结果的平均绝对百分比误差XMAPE对比。不同预测模型运算时间的预测时间如图6所示。

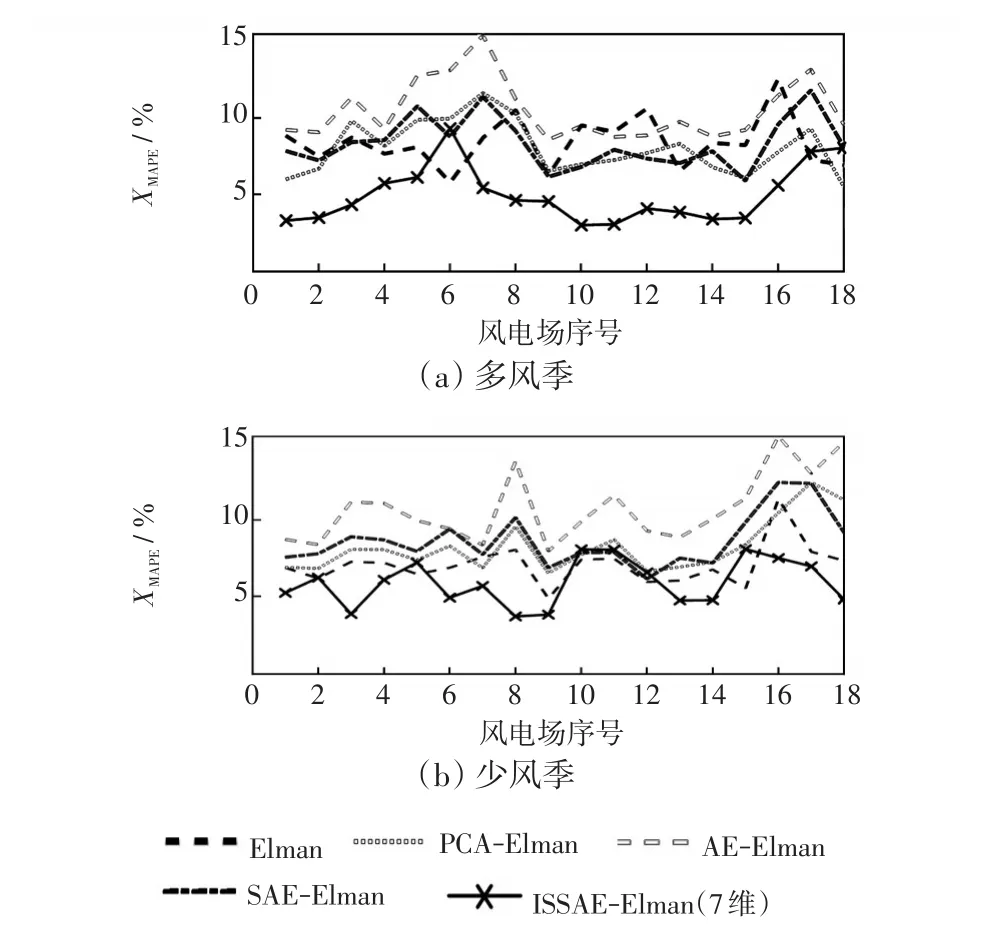
图5 18座风电场的MAPE误差对比Fig.5 Comparison of MAPE among 18 wind farms

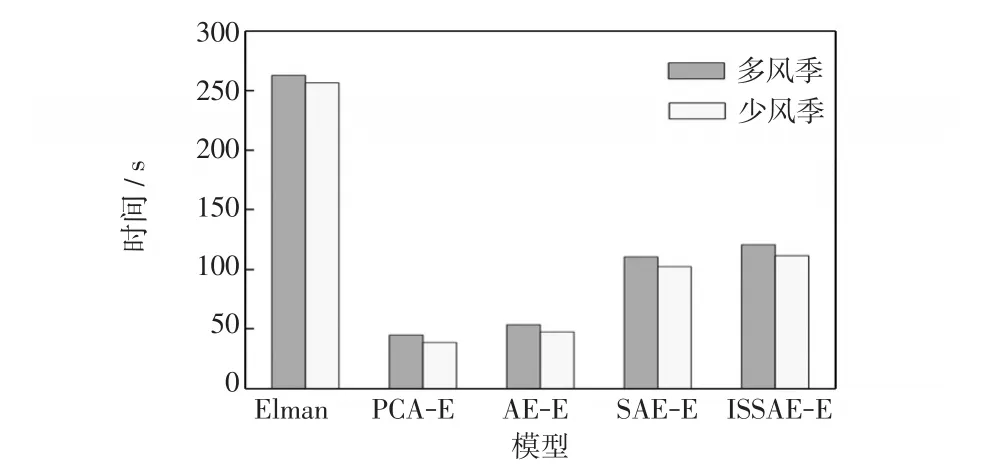
图6 不同预测模型运算时间Fig.6 Computation time of different forecasting models

从表2和图5可以看出，ISSAE-Elman模型在多风季与少风季均可得到最佳的预测精度，同时多风季的预测误差XMAPE比少风季的略高1.1%。将ISSAE-Elman与Elman直接预测模型对比，在预测精度方面，ISSAE-Elman对18座风电场多风季预测功率的XMAPE和XRMSE统计平均值分别低于不降维Elman直接预测模型2.23%和22.5%；少风季预测功率的XMAPE和XRMSE统计平均值分别低于Elman模型2.27%和21.20%。

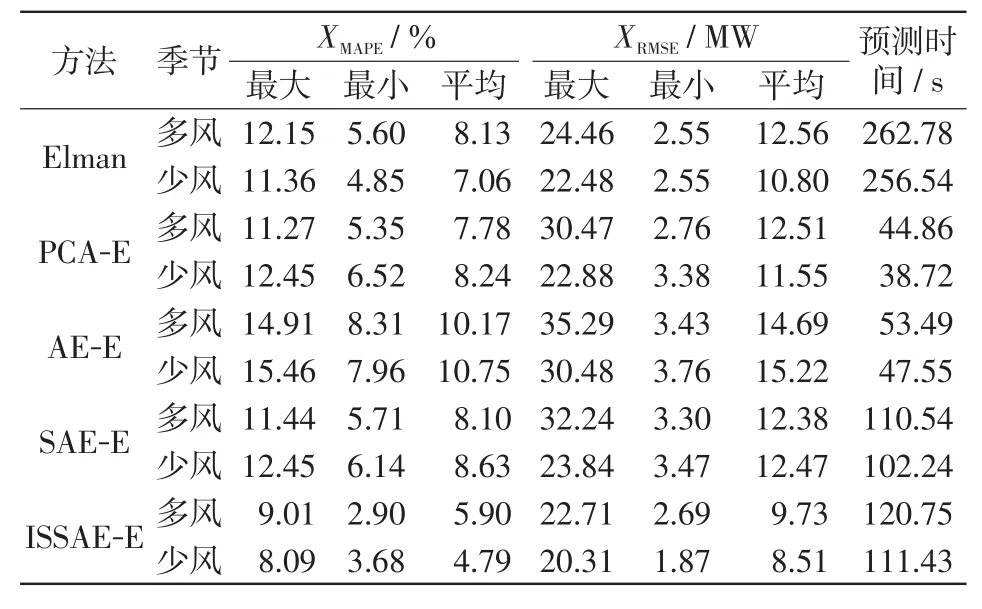
表2 18座风电场风电功率预测误差对比Tab.2 Comparison of wind power prediction errors among 18 wind farms

将ISSAE-Elman与同样采用降维-预测-重构框架的PCA-Elman和AE-Elman两种模型对比，观察表2和图5发现，ISSAE-Elman在多风季的平均误差XMAPE比PCA-Elman和AE-Elman分别下降了1.88%和4.27%，平均误差XRMSE也分别下降了22.2%和33.76%；在少风季平均误差XMAPE比PCA-Elman和AE-Elman的分别下降3.45%和5.96%，平均误差XRMSE也分别下降26.3%和44.09%。此外，ISSAEElman的XMAPE和XRMSE的最大、最小误差值显著低于其他2种模型，可获得更高的预测精度。

在预测效率方面，观察图6发现，ISSAE-Elman模型在多风季预测计算时间比直接预测的Elman降低了54%。由此可见，与Elman直接预测模型相比，ISSAE-Elman通过提取原始多维风电功率预测变量中相互独立的特征，实现独立特征并行预测，并减少预测变量间的相互影响，可有效提高计算效率。与同样采用降维-预测-重构框架的其它模型相比，ISSAE-Elman比PCA-Elman和AE-Elman模型结构更复杂，故计算时间有所增加，而与结构相似的SAE-Elman模型的计算时间相当。

3.3 稀疏、独立和限制性技术采用前后对比

图7分别给出了两季ISSAE-Elman、SAE-Elman、以及在ISSAE-Elman的基础上分别去掉稀疏、独立、限制性约束后3种模型的误差XMAPE统计值对比。

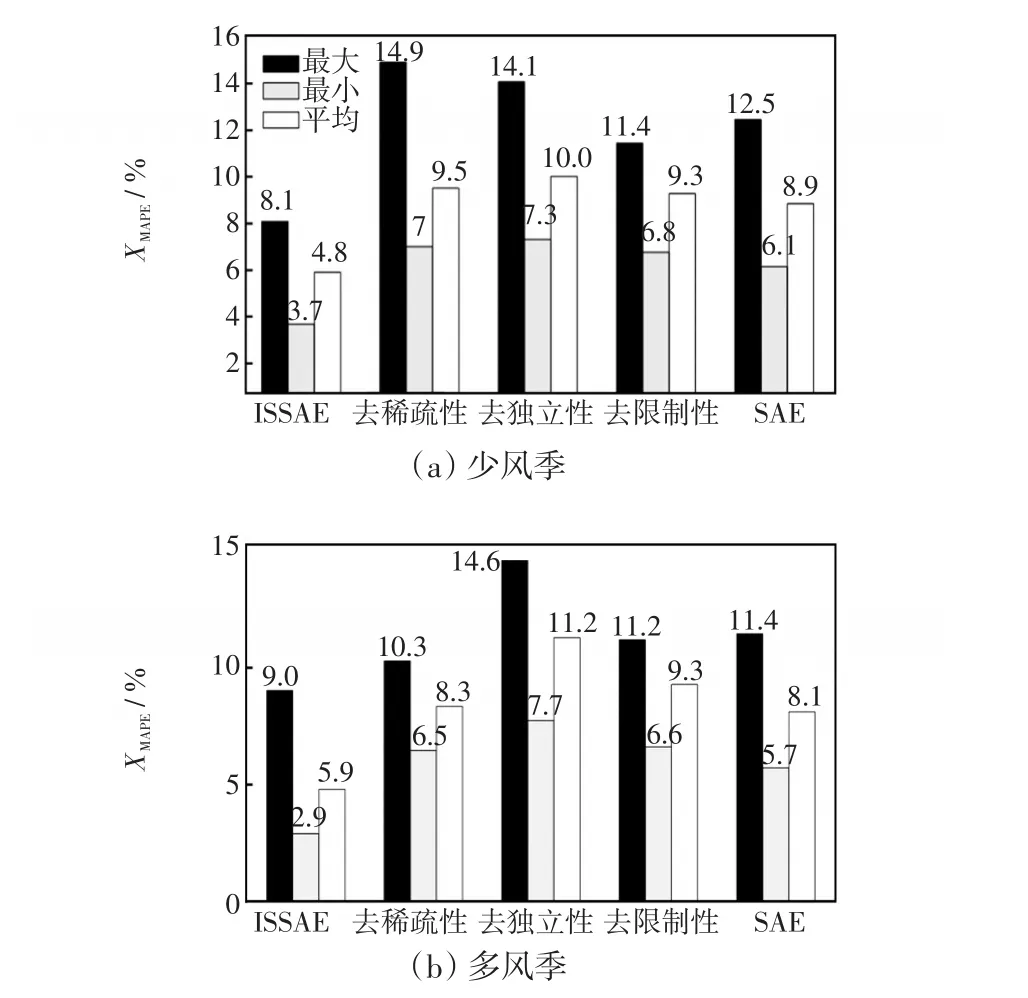
图7 18座风电场MAPE统计误差对比Fig.7 Comparison of statistic MAPEs among 18 wind farms

观察图7发现，在分别以及全部去掉稀疏性、独立性、限制性约束的4种情况下，少风季ISSAEElman的平均XMAPE分别下降4.7%、5.2%、4.5%和4.1%，最小XMAPE下降2.4%～3.6%，最大XMAPE下降3.3%～6.8%，多风季ISSAE-Elman的平均XMAPE分别下降2.4%、5.3%、3.4%和2.2%，最小 XMAPE下降2.8%～4.8%，最大 XMAPE下降1.3%～5.6%。综上，在SAE中引入稀疏性、独立性和限制性技术，可进一步改善多风电场功率预测精度。

3.4 模型参数对降维效果的影响

采用验证集对预测模型的降维维数r、堆叠自编码器个数L等超参数进行寻优的结果如下。

1）降维维数r

随着预测模型降维维数r变化，18个风电场的平均XMAPE变化曲线如图8所示。

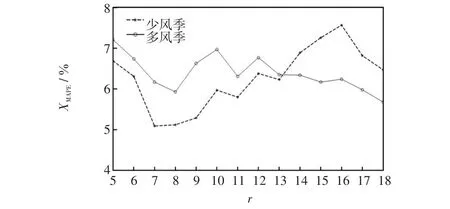
图8 XMAPE误差随r变化的曲线Fig.8 Curves ofXMAPEvs r

由图8可见，多风季和少风季当r在5～7范围内变化时，随着目标维数r的增加，平均XMAPE逐步降低；当r＞8之后，多风季随r增加，平均XMAPE变化出现波动；r＞12后趋于缓慢降低。而少风季随着r增加，平均XMAPE变化出现波动且呈上升趋势，r＞16后缓步下降。经综合权衡，算例最佳r宜选为7。

2）自编码器个数L

为比较不同自编码器堆叠数量对预测结果的影响，图9给出了堆叠自编码器个数L从1～4变化时18座风电场的平均XMAPE预测误差变化曲线，其中L=1对应单自编码器直接降维的情况，L＞2对应的自编码器均进行等维映射。

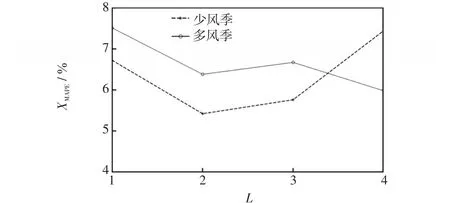
图9 XMAPE误差随L变化曲线Fig.9 Curves ofXMAPEvs L

从图9中可以发现，当堆叠自编码器增加到2个时，多风季的平均XMAPE降低1.13%，少风季的平均XMAPE降低1.32%。但当堆叠数进一步增多时，少风季的平均 XMAPE不降反升，增加0.34%和2.02%；多风季的平均XMAPE出现波动先增加0.29%后降低0.4%。这是因为随着自编码器个数L的增加，隐含层数（2L-1）也随之增加，神经网络结构加深将导致运算过程复杂，面临更严重的梯度弥散问题而影响训练效果。因此，本文最终选用2个自编码器堆叠。