面向分布式电源并网的多谐波源责任划分
2022-03-15阮正鑫邵振国陈育欣
张 逸,阮正鑫,邵振国,林 芳,陈育欣
(1.福州大学电气工程与自动化学院,福州 350116;2.国网福建省电力有限公司电力科学研究院,福州 350007;3.国网福建省电力有限公司石狮市供电公司,石狮 362300)
随着国家大力倡导电力系统由以化石能源为主向低碳可再生能源为主转型,大量的分布式电源DG(distributed generation)接入电网,导致系统内的谐波问题越来越突出[1]。大多数DG并网均具有故障性、波动性、多样性等特点,这使得当今配网谐波源的状态更加复杂多变[2]。因此在当前配网形势下,对如何准确划分多谐波源的责任进行研究具有重要的意义。
迄今为止,国内外对谐波责任划分的研究主要是针对谐波阻抗和背景谐波电压的计算方法,其中很多是基于波动量法和线性回归法的优化。文献[3-4]利用改进波动量法来求取谐波阻抗,进而算出谐波源责任,但波动量法的不足之处在于需要谐波电压与电流信号有足够大的波动,且对谐波测量的精度有较高的要求;文献[5-7]利用不同线性回归方法估计多谐波源谐波责任问题。线性回归法原理简单、求解方便,但近几年,随着越来越多DG的并网如光伏、电动汽车充电桩、高铁等谐波源,同时由于各DG的间歇性、波动性、多样化等特点,使得配电网谐波情况多变且迅速[8-9],进而导致背景谐波波动大,使得谐波电压和谐波电流已不再服从对称分布,即出现左偏(右偏)分布或散布较大的情况[10]。传统线性回归无法描述全部谐波电流或电压的变化规律,拟合结果无法体现谐波源的全部信息,导致谐波责任估算结果偏差较大,方法已经不再适用。除此之外,由于光电、风电等DG的日功率曲线具有较强波动性,导致其出力不再仅服从正态分布,而是出现多个分布组合的特点[11-13],传统线性回归无法识别分布的变化,导致拟合结果不再能提供有用的信息[14]。文献[15]首次采用分位数回归划分用户谐波责任,精度优于传统回归方法,但由于回归结果易受到分位点设置的影响且在实际运用中无法选取合适的分位点,因此工程实用性较差。
针对现实中背景谐波电压波动的问题,传统的波动量法不能抑制背景谐波波动的影响,而线性回归方法并不适用于背景谐波波动大的情况。目前,有不少学者采用数据聚类的方法先对背景谐波进行处理[16-17],其研究思路是对背景谐波数据进行聚类处理,从而将分析时段划分为若干个子时段。然而由于DG出力的随机波动性、人为测量误差、传统估算阻抗方法[18-20]估算精度不足等问题,导致传统聚类方法对背景谐波电压进行聚类时获得的背景谐波数据中常常存在一些“奇异值”,一方面,其将导致背景谐波聚类中心结果远离密集区域,趋向离群区域,造成谐波责任估算结果出现错误;另一方面,由于“奇异值”的存在会对初始中心点的选取造成影响,迭代次数增大,导致较差的背景谐波聚类结果,进而导致谐波责任估算结果不理想。
本文针对DG接入配网导致的谐波随机性、波动性强等特点,提出了OFMMK-means算法与复合分位数回归相结合的多谐波源责任划分方法。首先利用基于离群因子和最大最小算法的优化K-means初始中心选择算法对背景谐波电压进行聚类,其次基于聚类结果利用复合分位数回归对各用户进行谐波责任划分。最后通过算例仿真表明本文提出的方法准确度高,且在背景谐波波动大仍适用。
1 谐波责任划分指标

图1 多谐波源等效电路Fig.1 Equivalent circuit of multiple harmonic sources
谐波源用户i在PCC处产生的谐波责任为Ui在PCC处电压Upcc上的投影。以公共点接入3用户为例,Upcc和Ui(i=1,2,3)与背景谐波电压U0之间的相量关系如图2所示。
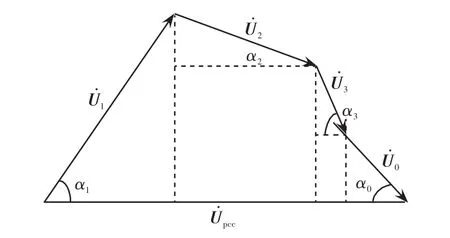
图2 谐波电压相量投影Fig.2 Phasor projection of harmonic voltage
用户i在PCC处的谐波责任指标[15]为
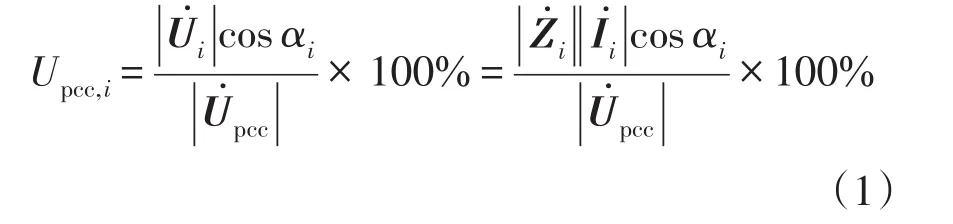
式中,αi为的夹角。和 αi均可通过测量获得,为谐波阻抗,表示除了谐波源i以外其他谐波源等效谐波阻抗的并联,其中i=0,1,2,3。
根据图2相量关系可得

式(2)可等效为
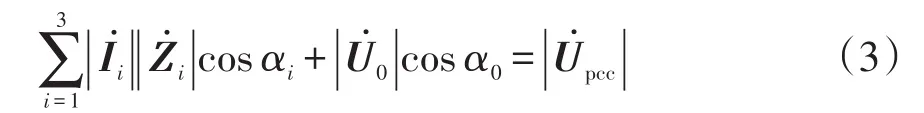
2 复合分位数回归基本原理
2.1 分位数回归
Koenker和Bassett[22]在1978年首次提出分位数回归的概念,其在中位数回归的基础上进行推广得到分位数的回归模型[14]。与最小二乘回归相比,前者通过求解残差平方和进而估计参数,后者则是通过求解加权残差和求解估计参数。第p回归分位可以定义为分位数回归最小化问题的任意解,即
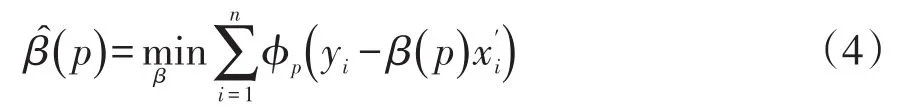
式中:φp为权重函数;yi和xi为第i个数据点;n为样本总个数。φp(u)表示为
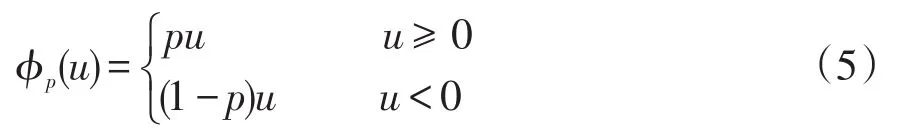
式中,u为权重函数φp中的自变量。
图3为利用不同回归方法拟合的结果。图中数据点采自利用PSCAD仿真软件搭建的图1仿真模型中PCC点的5次谐波电压电流幅值,黑点表示,实线表示不同分位数 τ(τ=0.1,0.2,···,0.9 ,自下而上)下拟合的结果,虚线为偏最小二乘回归拟合的结果。
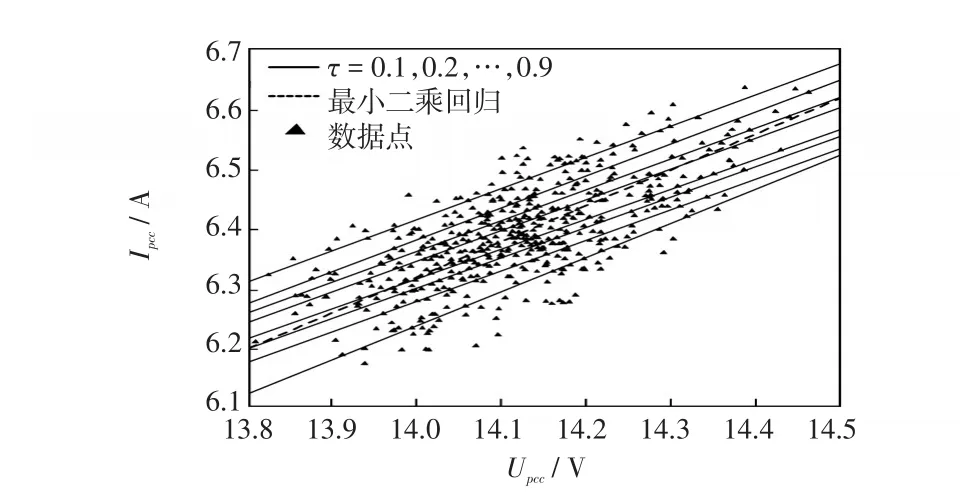
图3 分位数回归与最小二乘回归的比较Fig.3 Comparison between quantile regression and least square regression
最小二乘估计往往使那些远离群体的数据(很可能是异常值)对残差平方的影响比其他数据大得多。从图3可以看出,由于受到异常值的影响,最小二乘回归曲线偏离了正常模式,分位数回归则涵盖了大量的数据点。与最小二乘法相比,分位数回归的应用范围更广,其不仅能够度量变量在全局的分布,当误差不服从正态分布时,分位数回归依旧能够保持较高的稳健性,虽然分位数回归无法获得精确的估计值,但可以刻画不同分位数下的数据分布情况,从而捕捉更多的数据信息。
2.2 复合分位数回归
从以上分析可见,虽然分位数回归效果较最小二乘回归更优,然而也有许多分位点的估计效果要比最小二乘差,同时,分位数回归估计的效率也容易受到分位数特定取值的影响[24],为了避免上述问题,本文采用了复合分位数回归的方法。
假设一组分位点为 0<p1<p2<…<pk<1,与分位数回归类似,有
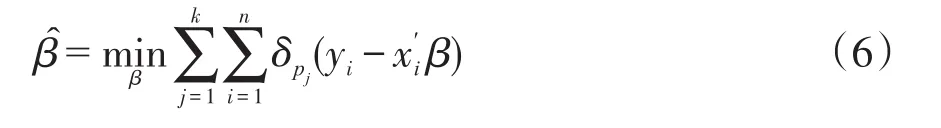
式中:k为分位点个数;pj为设定的 j个分位点;δpj为复合分位数的损失函数,表示为
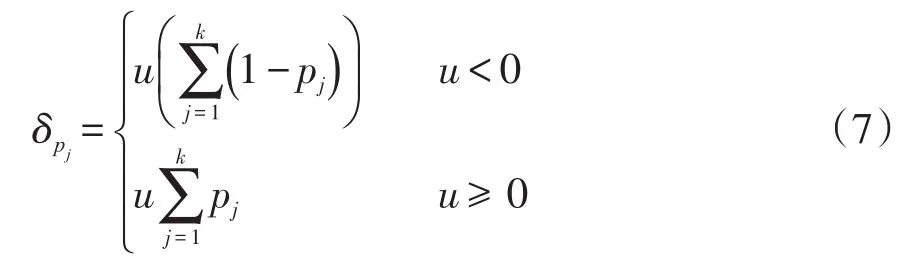
对比式(5)和式(7)可知,分位数回归损失函数的加权和即为复合分位数回归的损失函数。相比于传统的回归方法,复合分位数对模型的随机误差项没有任何假设性要求,不必迁就远端数据,可以更大程度地提供数据的全部信息,稳健性好[25-26]。同时,该回归算法弥补了分位数回归不能完全反映数据整体信息、实际运用中无法选择合适分位点等不足,具有更强的稳健性和稳定性,可以有效提高谐波责任划分的精确度。
3 数据的选择
3.1 有效数据段的选择
与传统配电网不同的是,高比例光伏的并网使得谐波阻抗特性不再是固定不变的,而是具有时变性[26-27]。因此需要提出更加有效的数据选取方法,选出光伏接入后谐波阻抗与背景谐波电压变化较小的数据段。定义系数δup和δdown来衡量谐波电流波动程度,表示为
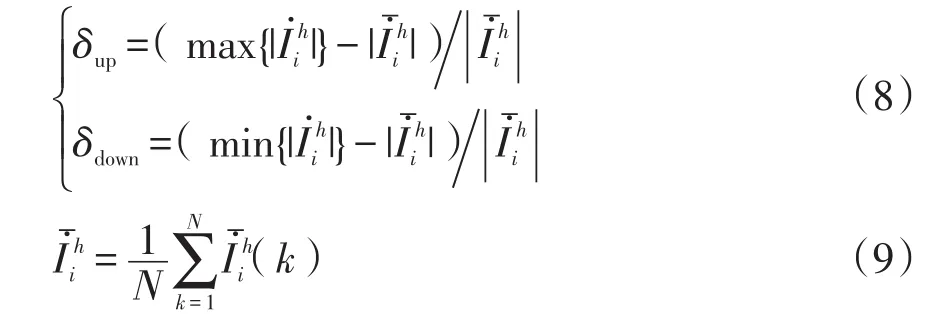
通常情况下,各用户谐波电流以及节点电压的波动主要由以下2个原因导致[28]:一是系统运行方式发生改变或者其他负荷的切除或接入引起的谐波阻抗不再固定不变;二是由谐波源用户自身运行状态变化引起的谐波波动。前者造成的谐波波动由于回归模型系数发生改变会影响回归计算的精度,应予以去除。后者则是谐波源的正常波动,是估算系统阻抗的基础,应予以保留。由文献[29]可知:当波动系数δup>0.1或δdown<-0.1时,则可判断谐波波动为第1种情况,即认为该数据段中回归模型系数发生改变,应舍去该数据段;否则,保留数据。
3.2 OFMMK-means算法
由于传统的聚类方法对聚类中心初值的选取以及远端数据较为敏感,大量DG接入带来的波动性使得传统聚类结果误差增大。因此本文采用一种改进的K-means算法[30],其具体步骤如下。
步骤1计算数据点i(i=0,1,2,3)的离群因子为

式中:lrdk(i)(或lrdk(j))为数据点i(或j)局部可达密度,该值越小,密度越小,表示数据点与周围数据点距离越远,越可能是离群点;Nk(i)为点i的第k距离[30]邻域,就是i的第k距离以内的所有点,包括第k距离。
步骤2将每个数据的离群因子按从小到大排列,并记作集合QL。
步骤3在集合QL中选取前 δn(0<δ≤1,n为数据集的大小)个数据点作为候选初始中心点,记作集合QLL。
步骤4在集合QLL中随机选取一个数据点C1作为第1个聚类中心。
也就是当点P(1,1)不变时,D换成y轴上除原点外的其他点,结论就不成立了,因此抛物线的方程是由点P(1,1)决定的,这说明D与P之间是有联系的.
步骤5对集合QLL中除了数据点C1之外的数据分别进行与C1的欧式距离计算,并选出最大值作为第2个聚类中心C2。
步骤6计算集合QLL中除了数据点C1、C2之外的所有样本到聚类中心C1、C2的距离,记作
步骤7若且 D3>D12φ(D12为C1到C2的距离,φ为检验参数,通常取0<φ<1),则作为第3个聚类中心C3。
步骤8重复步骤7,直到Di<D(i-2)(i-1)φ,结束寻找聚类中心,输出k个聚类中心。
3.3 谐波责任划分

4 算例分析
4.1 谐波责任仿真结果分析
为验证本文所提方法的准确性,基于PSCAD仿真软件搭建了如图4所示的仿真模型。其中,共接入3个谐波源用户、1个DG(光伏发电系统)以及普通线性负荷。在各谐波源电流中加入其额定值的10%的随机波动来模拟配电网中实际负荷的波动情况。因光伏发电系统主要由光伏电池模块,DC/DC功率变化模块,逆变器模块组成。本文建模采用一种典型的两级拓扑的光伏并网发电系统对光伏进行精确建模。采用电感与电阻并联的形式来模拟线性负荷,额定容量为2 MW。以A相为例对用户Hi(i= 1,2,3)5次谐波责任进行计算分析,其中系统侧(用户侧)谐波阻抗为电阻R与电抗L的串联,仿真设置如表1所示。
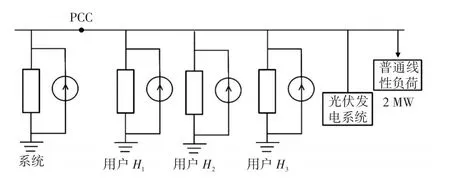
图4 仿真模型Fig.4 Simulation model
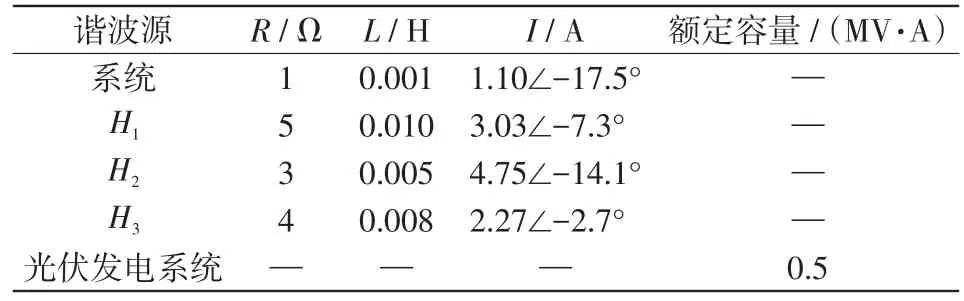
表1 谐波源数据Tab.1 Data of harmonic source
4.1.1 无DG接入

图5 各用户谐波责任结果Fig.5 Harmonic contribution results of each user
图5给出了不对背景谐波电压进行处理时,直接利用偏最小二乘回归、稳健回归、复合分位数回归得到的各用户的谐波责任情况。从图5可以看出,本文方法在背景谐波电压变化时能有效提高谐波责任划分的精度。
为验证本文方法的适用性,当图4中DG未接入时,在系统侧谐波电流加入均值为0、方差分别为0.15、0.20、0.25的随机扰动,在用户侧加入均值为0、方差为0.05的随机扰动,分别采用文献[16]均值漂移法以及本文所提方法对各用户谐波责任以及误差进行计算分析,结果如图6所示。其中本文聚类算法中的聚类对象包含幅值和相角2个属性,值取0.4[30]。
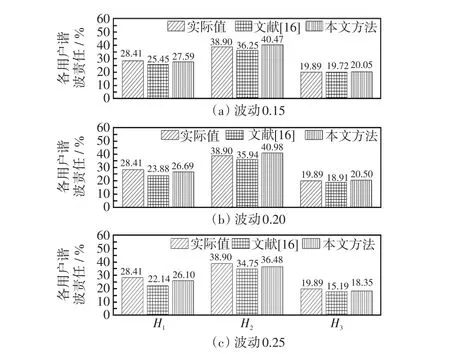
图6 无DG接入时各用户谐波责任结果Fig.6 Harmonic contribution results of each user without DG
从图6可以看出,与文献[16]相比,由于本文聚类算法克服了异常点以及初始中心点选取影响的缺点,同时,复合分位数能够更大程度地涵盖数据信息,使得结果更加精确。
4.1.2 DG接入
为分析光伏电站出力的分布特性,以福建漳浦某屋顶光伏数据作为基础进行研究。所选取的数据时间为24 h,测量时间间隔30 s,对光伏出力数据进行统计分析,同时将光伏出力实测数据接入如图1所示的仿真结构中,根据文献[32]计算背景谐波电压U0,结果如图7所示。其中横坐标为光伏有功功率、背景谐波电压有效值,纵坐标为概率密度。
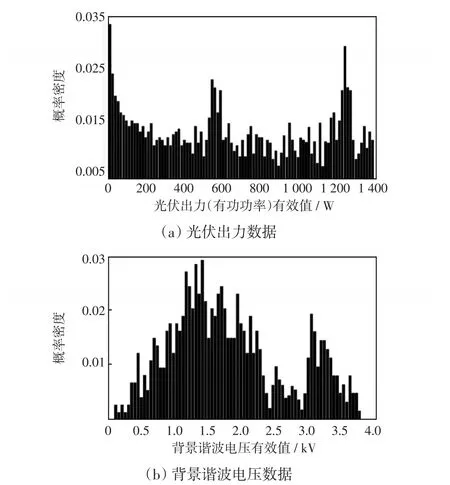
图7 光伏出力数据以及背景谐波电压U0概率分布直方图Fig.7 Probability distribution histogram of photovoltaic output data and background harmonic voltageU0
从图7(a)可以发现,光伏全天出力会出现除正态分布之外的非对称以及重尾分布[33-34],进一步计算其偏度、峰度等参数可知:①有偏性,分布偏度为-0.26,分布向左偏移并倾斜,轴线(众数)两侧并不对称;②多峰性,出现多个局部峰值,呈现多峰特性。
从图7(b)图可以发现,背景谐波电压同样会出现除正态分布之外的非对称、多峰等分布特点,其中较高峰为系统背景谐波产生的,较矮峰为分布式电源的接入与背景谐波叠加产生的[35]。结合文献[11]可知,PCC点电压的波动主要由光伏出力波动、电网阻抗角和系统短路容量3个因素决定,若接入位置、配网给定,则电网阻抗角以及短路系统容量均为定值,PCC点处电压波动只取决于光伏出力波动。由文献[16]可知,若假定系统阻抗不变,由于PCC点处谐波电流波动较小,因此背景谐波电压波动取决于PCC点处电压波动的情况。综上,可认为背景谐波电压分布与光伏出力分布含有类似的特征。故采用传统线性回归将无法描述背景谐波电压准确信息,从而导致谐波责任划分结果出现误差。
为验证本方法在DG并网导致背景谐波波动增大时的准确性,接入如图4所示的DG。为模拟光伏接入造成背景谐波电压波动,在光照与温度中加入均值为0、方差为0.15和0.20的正态波动,从而使得光伏发电系统输出功率波动来近似模拟背景谐波电压波动,如图8所示。以5次谐波为例进行分析,将文献[16]与本文方法进行对比计算,结果如图9所示。
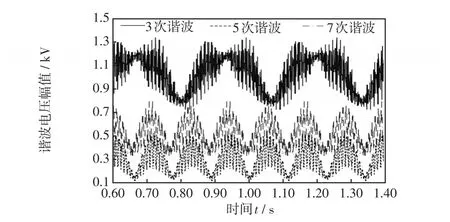
图8 光伏并网点处谐波电压幅值Fig.8 Harmonic voltage amplitude at photovoltaic gridconnected point
从图9可以看出,本文方法在DG接入后依旧能得到较高精度的结果,这是由于分布式电源输出的不确定性导致背景谐波出现较多的奇异值,本文聚类方法能够较好地解决奇异值对聚类结果的影响。同时,复合分位数回归的实质是各分位点下分位数回归的综合估计结果[25],相较于传统最小二乘回归能够更大程度地捕捉波动剧烈下的谐波电压电流的特征,从而得到更高精度的谐波责任结果,且本文方法不需要对分位点进行选取,在工程上有较高的实用价值。
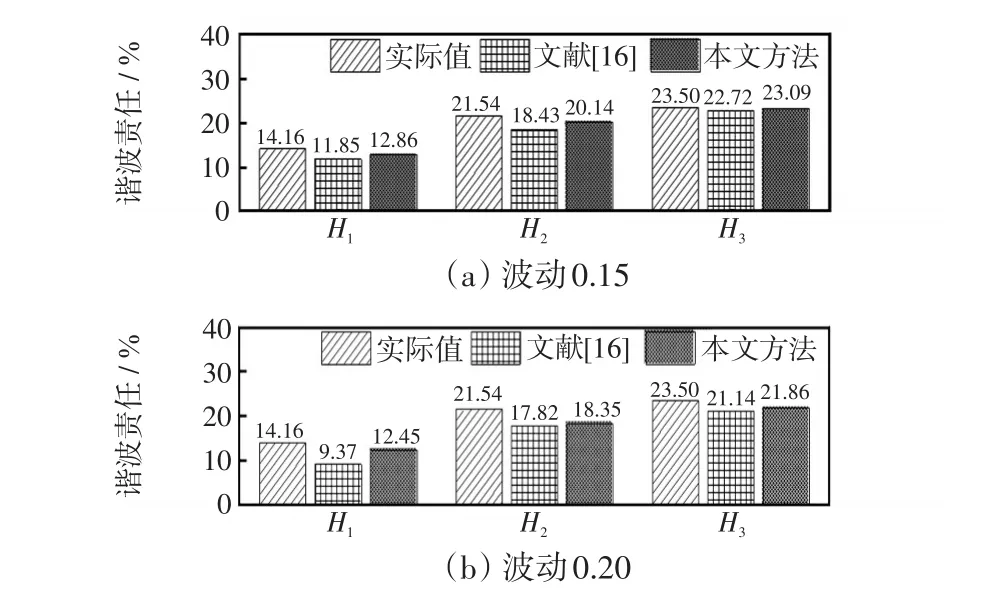
图9 DG接入时各用户谐波责任结果Fig.9 Harmonic contribution result of each user with DG
4.2 实例验证
为了验证上述方法在实际工程中的可行性,本文对漳州市某供电局下10 kV母线所连各用户进行测试分析。各用户参数如表2所示。图10为含DG谐波责任划分场景。其中10 kV母线为关注母线,用户C为发电全额上网的分布式光伏,计算假设用户C为背景谐波时的用户A、B的谐波责任。

表2 光伏逆变器参数Tab.2 Parameters of photovoltaic inverter
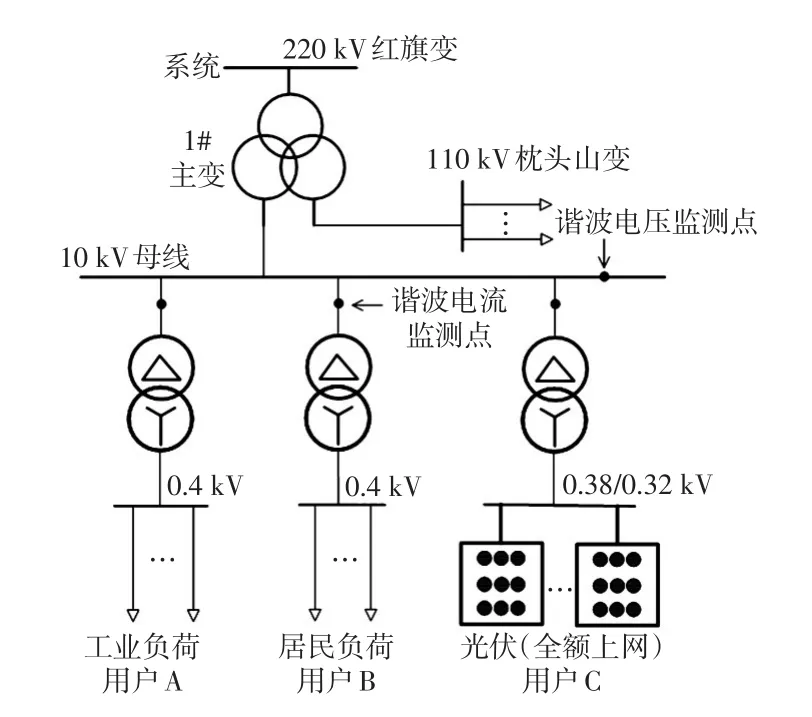
图10 现场测试结构Fig.10 Structure of field test
现场实测数据包含10 kV母线以及用户A、B、C出口处谐波电压、电流数据。谐波电压(电流)数据为5次谐波电压(电流)95%的概率,数据间隔为3 s,数据波形如图11所示,谐波责任划分结果如表3所示。
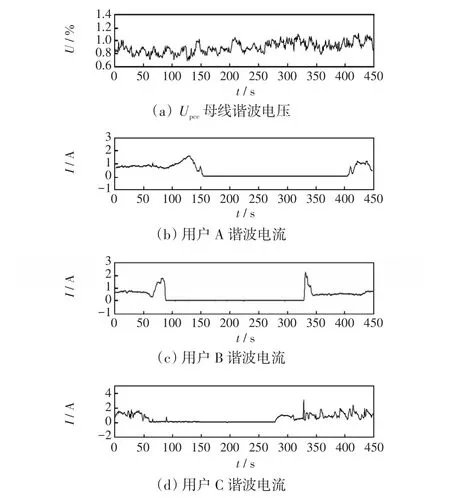
图11 各测试点5次谐波电压、电流波形Fig.11 Waveforms of 5th harmonic voltage and current at each test point

表3 谐波责任指标实例Tab.3 Example of harmonic contribution index
从表3中可以看出,用户A、B的责任仅为18.76%、13.35%,用户C(背景)的谐波责任高达52.47%,应承担主要谐波责任。从实测数据结合现场调查可知,用户C有大量光伏接入,导致5次谐波发射量较大,为主要谐波源。本文方法结果与实际相符,具有一定的工程实用价值。
4 结论
本文面向DG大量接入导致的谐波波动大问题,提出OFMMK-means算法与复合分位数相结合的多谐波源谐波责任划分方法,结论如下。
(1)DG的接入导致背景谐波波动增大,本文所提OFMMK-means聚类算法可有效提高背景谐波的抗误差性,进而提高了谐波责任划分的准确性。
(2)DG的接入导致背景谐波电压呈非对称分布,所提出的回归方法能够适应非对称分布情况,更大程度上提供数据的有用信息,进而提高谐波责任划分的精度。
(3)本文所提方法在DG接入导致背景谐波波动增大时仍可适用,具有鲁棒性强和精确度高的优点,可用于谐波责任的准确划分,有一定工程应用价值。
