变截面柔性机械臂固有频率测定方法研究

夏瑞强，任 豪，梁开旭

(长安大学工程机械学院，陕西 西安 710064)

0 引言

为了增加刚度，传统的机械臂尺寸较大，导致其不能应用于轻量化、高灵活性、高精度的场合。为了满足各行业的实际需求，并实现机械臂功能的多样化，现在越来越多的机械臂采用变截面结构和具有柔性的材料。与刚性机械手相比，柔型机械臂具有更高的速度、更好的能量效率、更高的机动性和更高的有效载荷与臂重比等优点。同时，变截面结构在满足了机械梁臂承载能力的前提下，较好的实现了结构内部优化，减轻了重量，节省了材料和成本[1-5]。然而，变截面柔性臂是一个复杂的分布参数系统，具有高度耦合性，这就使得其系统变得非常复杂，特性参数难以确定。因此本文以航空铝材变截面柔性机械臂为研究对象，建立数学模型，并对其固有频率测定方法进行研究。

1 柔性机械臂动力学建模

针对机械臂的建模研究一般都将机械臂等效为变截面梁[4]，同时变截面梁材料具有等效果的柔性，使得变截面梁满足机械梁臂的承载能力的同时，降低了系统的重量，增加了灵活性，减少了成本。

由振动力学[11]可得本文的研究对象属于欧拉-伯努利梁，其横向自由振动微分方程为：

(1)

其中，变截面机械臂中横截面积A(x)和截面惯性矩I(x)是随长度x变化的函数[6]，EI表示臂的抗弯刚度。

(2)

将机械臂的运动简化为如图1所示的[8]运动模型，则由数学知识可知臂上任意一点的坐标可表示为：

(3)

则可得到系统的动能T和势能V分别为：

(4)

(5)

式中：In为旋转中心转动惯量，E为弹性模量，L为臂长，ρ、A分别为机械臂材料密度和横截面积，θ为柔性机械臂的旋转角度。

应用Lagrange动力学方程可得：

(6)

式中：u为广义力向量；qi为广义位置向量，L=T-V。

联立上式可得动力学方程为[9-10]：

(7)

式中：σi为模态阻尼系数，Wi(l)为形状函数。

2 微元法求解固有频率

由上述可得变截面柔性臂横向自由振动微分方程以及动力学方程，且由高等数学微分方程求解可设：

y(x，t)=Y(x)M(x)

(8)

Y(x)=Asinφ+Bcosφ+Csinhφ+Dcoshφ

(9)

为了方便解出该四阶自由振动微分方程，采用微元法将变截面机械臂划分为无数个近似等截面小段，如图2所示[5]，则单位长度的弯曲刚度和线密度表达式如下[1]：

(10)

此时，梁上第i段自由振动的方程为：

(11)

由公式(8)、公式(9)可知：

yi(x，t)=Yi(x)Mi(x)

(12)

Yi(x)=Aisinφ+Bicosφ+Cisinhφ+Dicoshφ

(13)

联立上式可得：

(14)

由于采用微元法将机械臂分成n个小段，当n足够大时，每个小段可近视看成等截面机械臂，并且相邻两个小段在边界处的各项参数近似相等，故有：

Yi(xi)=Yi+1(xi+1)

(15)

本论文研究的航空铝材机械臂属于悬臂结构，则在x=0，x=L处分别有：

(16)

(17)

将式(15)转换成矩阵形式[5]有：

(18)

联立上式即可得到：

MiHi=Hi+1

(19)

其中：

Hi=[AiBiCiDi]T，

Hi+1=[Ai+1Bi+1Ci+1Di+1]T

(20)

式中，Mi为中间的传递矩阵，Hi和Hi+1为臂上第i段和第i+1段臂之间的待定系数向量。

联立上式，并结合边界条件公式(16)、公式(17)即可求得固有频率。

以本论文研究对象航空铝材柔性机械臂为例进行计算，材料参数如表1所示[8]，结合上述方法以及边界条件即可求得前三阶固有频率分别为4.892 Hz、26.321 Hz、70.546 Hz。

表1 航空铝材机械臂各项参数

3 机械臂固有频率测定

对于比较简单的运动系统，一般会利用牛顿第二定律法、动量距定理法、拉格朗日法和能量守恒法等方法求其固有频率。求解方法通常都是对系统进行分析得出系统的微分方程，求解该方程所对应的特征方程的特征根，得到系统的固有频率。本章节首先通过衰减曲线法利用实验平台测其固有频率，然后利用ANSYS Workbench进行仿真验证研究。

3.1 影响固有频率的因素

一般将柔性机械臂的弹性动力学方程表述为如下形式[7]：

(21)

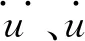
对式(21)求解，由振动力学[11]和数学知识推导可知，固有频率的表达式如下：

|F2E-M-1K|=0

(22)

式中：F为固有频率，E为单位矩阵。

由公式(22)可知，质量矩阵M和刚度矩阵K决定了其系统的各阶固有频率，质量矩阵M与研究对象的材料参数和几何参数相关，而刚度矩阵K与材料本身的惯性矩、横截面积、弹性模量等物理性质以及本身的几何形状有关，而与本身受力和支撑情况无关。因此，柔性机械臂的这些因素决定了其固有频率的大小。

3.2 振动-衰减曲线法测固有频率

系统的固有频率是指系统在受迫而产生运动时产生的共振频率，因此，对臂施加外力，使其产生受迫运动，然后采用NI CRIO-9046嵌入式控制器和NI9237采集卡组成的数据采集系统将应变片上的应变数据利用串口通讯的方式传递到上位机。利用Labview控制软件将其变化波形实时显示，并将实时数据保存，如图3所示，之后利用Matlab软件对采集到的数据进行处理后，对处理后的数据进行快速FFT变换，即可得到柔性机械臂相应的固有振动频率，如图4所示，前三阶固有频率分别为4.883 Hz、26.07 Hz、70.69 Hz。

3.3 仿真验证

利用有限元仿真软件ANSYS对上文利用微元法的计算值以及实验测出的固有频率值进行仿真验证。首先打开Workbench中的模态分析Modal模块，如图5所示。由表1 可知本文研究的航空铝材机械臂各项参数，然后依据各项参数在Engineering Data模块设置材料属性，如图6所示。在Geometry中建立模型。然后对其进行网格划分、施加相应的固定约束，最后进行各阶固有频率的分析，分析结果如图7所示，前三阶的固有频率分别为5.0995 Hz、26.692 Hz、70.849 Hz。

由以上方法得出变截面柔性机械臂固有频率，结果如表2。经实验和仿真得到的固有频率，与利用微元法计算的值相比误差均在5%以内，表明所用方法的正确性。

表2 固有频率计算结果(单位：Hz)

4 结论

本文以航空铝材变截面柔性机械臂为研究对象，首先建立了动力学模型并基于微元法对其固有频率进行计算，求出前三阶固有频率，并分析影响固有频率的因素，然后利用实验的仿真微元法求出的值进行验证，数据表明方法的正确性。