基于模型预测控制算法的永磁同步电机无传感器控制

芦振宇，赵方熠

(长安大学工程机械学院，陕西 西安 710064)

0 引言

永磁同步电机的矢量控制技术通常包括转速控制、电流控制和PWM控制算法3个组成部分。由于电机的转速和电流控制需要将给定的值与反馈回来的值作对比，因此，在电机控制方式中观测反馈信号又分为有传感器的和无传感器的，有传感器的伺服系统需要在电机转轴上安装编码器或者传感器来测量转子运行位置和转子速度参数，然而安装这些传感器会导致电机转动惯量、尺寸和体积的增大，并且安装时由于安装工艺问题，会使得系统可靠性降低[1]。无传感器的反馈系统就不需要考虑上述的问题，因此，采用无位置传感器的反馈控制系统已逐步成为研究热点。

在本文假定的低、零速的工况下，常用的无传感器控制方法有旋转高频信号注入法[5]、脉振高频信号注入法[6]与高频方波信号注入法[9]等。但是这些控制方式都是使用PI调节器对电机的交直轴电流分别进行控制，而这种控制方式始终需要等待观测器计算反馈回来的信号，再将这些信号与给定的转速进行PI参数整定输出，这就导致系统控制器的输出总是滞后于系统的变化。因此引入模型预测控制可以减小伺服系统的估计误差，并且可以得到更好的电流动态特性。

本文以电机同步旋转坐标系下的数学模型为基础，在电机低、零速运行状态下，提出一种电流预测控制算法与脉振高频信号输入法结合的控制方式。最后通过仿真验证本文提出的控制方法。

1 脉振高频电压信号注入法

本文选定的电机是表贴式电机，并且选定工况是：电机转速处于低、零速的状态，因此本文选择脉振高频电压注入法作为本文的反馈信号观测器，该方法是通过在电压环的控制环节注入高频电压信号，将原本的电压信号与注入的电压信号共同施加给电机的绕组，然后通过滤波器将反馈回来的高频响应电流与电机电流分离，由于响应电流会携带转子位置信息，所以再通过计算估计出转子位置[2-4]。

1.1 脉振高频电压注入法原理

(1)

(2)

在d-q坐标系中，电机定子电感可以表示为：

(3)

在静止坐标系α-β中，式(3)转化为：

(4)

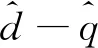
(5)

(6)

(7)

此时，高频电流可简化为：

(8)

1.2 转子位置估计

(9)

PI调节器的传递函数如式(10)所示。

(10)

其中，γp与γi分别为比例和积分增益。

根据图2所示的控制框图，我们可以将转子估计误差角与实际的转子位置角的传递函数表示为：

(11)

2 模型预测算法

模型预测算法有限控制集模型预测控制(FCS-MPC)和连续控制集模型预测控制(CCS-MPC)两类[9]。由于CCS-MPC是一种输出连续值的控制方式，所以需要输出无穷矢量，则无法通过穷举的方式进行寻找最优的值。因此，本文选择FCS-MPC作为电流控制的方式。但是电机参数不同会导致控制效果不同，因此针对需要解决模型与被控对象不相符的问题，引入一个反馈系统来校正克服不匹配的影响。本文将电机电压方程离散化后，通过在滚动的、有限时域内的优化指标进行优化。

首先给出电机的d-q坐标系下的电压方程：

(12)

其中，id、iq分别为d、q轴电流；ud、uq分别为d、q轴电压；Ld、Lq分别为d、q轴电感；R为定子电阻；ψf为永磁体磁链；ωe为转子电角速度。

由于使用电机采用高频信号注入法来获取转子位置，则Ld=Lq=L，可以选择电流为状态变量，采用前向欧拉离散法，将式(12)离散为式(13)：

(13)

式(13)对d-q轴的电流预测模型带入八个电压矢量，可以得到下一个控制周期的预测值，但是直接通过电流预测模型方法获取的预测值并不是此时的最优解，由于全局最优解对于一个复杂系统并不方便求解出来，因此本文选择通过构造一个代价函数，通过求取代价函数的最小值来获得次优的预测值。以下给出代价函数：

(14)

3 系统仿真

如图3所示，是在MATLAB/Simulink环境下搭建的，基于模型预测控制算法的有限控制集模型预测控制和脉振高频电压注入法的无传感器控制系统模型，该模型中使用脉振高频电压注入法作为观测器估计转子的位置和转速，并将模型预测控制算法的有限控制集模型预测控制替换电流环的PI调节器对电机的交直轴电流分别进行控制。其中，仿真模型中电机参数为：极对数pn=2；定子电感ld=5.2 mH，Lq=17.4 mH；定子电阻R=0.33 Ω；磁链ψf=0.646 Wb；转动惯量J=0.008 kg·m2；阻尼系数B=0.008 N·m·s。仿真条件设置为：直流侧电压Udc=311 V；PWM开关频率fpwm=5 kHz，高频电压信号的幅值Vin=20 V，频率fin=1000 Hz。

选取电机的运行工况为零、低速度状态，并且为了验证所搭建仿真模型即使在电机转速发生变化的情况下，也能准确、迅速的调节控制，因此本文将参考转速设定为在0～0.4s时Nref=50 r·min，在0.4～0.8 s时Nref=100 r·min，并且电机负载是空载，仿真结果如图4所示。

由以上仿真结果可以知道，转速稳定上升且稳定运行后转速估计误差逐渐减小，且转子位置估计误差逐渐减小。由图4(a)可以看出，转速最大的误差绝对值都小于0.2，并且随着转速稳定，估计误差也减小并稳定在一个较小的值。由图4(a)可以看出，电机在这个控制器控制下可以迅速反应，在0.4 s预设转速发生变化，该控制能够在0.02 s内迅速将实际转速稳定在预设转速附近。由图4(c)、图4(d)可以看出，位置估计误差的绝对值都小于0.01，表明本文设计的控制模型可以较为精确的估计转子位置。

4 结论

本文首先选取电机低、零速度运行工况，由电机低、零速运行出发，选取了脉振高频电压注入法作为电机运行时对转子位置和速度的观测方法，并对其进行数学建模，然后设计出电机的电流预测控制器与观测器结合控制电机转动。最后建立电机同步旋转坐标系下的数学模型，将上述两种算法进行仿真验证。仿真结果表明，本文提出的控制方法能够很好地实现电机低、零转速的控制，并且具有很好的稳态性能。