考虑进口预旋的阶梯型迷宫密封转子动力特性
2022-03-15李康迪周倩倩徐自力王鑫靳亚峰
李康迪,周倩倩,徐自力,王鑫,靳亚峰
(1.西安交通大学机械结构强度与振动国家重点实验室,710049,西安; 2.东方汽轮机有限公司产品研发中心,618000,四川德阳)
cross stiffness
密封是压缩机、汽轮机、液体火箭发动机涡轮泵、航空发动机等旋转机械用于控制工质泄露的关键部件[1]。转子偏心涡动时,密封动静部件之间的微小间隙形成的压力场会产生作用于转子的气流激振力[2],影响转子系统的动力特性,致使系统稳定性降低,严重时可能产生大幅低频振动,诱发转子失稳,影响机组的安全性和经济性[3]。因此,研究密封动力特性对保障转子安全高效运行具有重要意义。
20世纪80年代,Iwatsubo首次提出了理论求解迷宫密封转子动力特性的单控制体方法[4](Bulk Flow方法),晏鑫等采用Bulk Flow方法研究了孔型密封转子动力特性[5]。在实验方面,Ertas通过测量作用于静子的静态力和相对静态位移,得到了密封的直接和交叉刚度[6]。随着计算流体力学(CFD)方法计算效率和精度的提高,以及其能够给出密封内部流场细节等优点,采用CFD方法进行透平机械旋转密封转子动力特性的研究逐渐增多。Rhode等采用CFD方法求解了迷宫密封的转子动力特性系数[7]。交叉刚度导致转子的涡动轨迹更接近椭圆[8],Li等提出了转子轴心轨迹为椭圆形的求解模型,椭圆长轴的方向取决于激励的方向[9]。密封的转子动力特性系数具有很强的频率相关性[10],需研究其随频率的变化规律,Li等提出了一种转子多频椭圆涡动的动力特性求解模型,能够实现同时对多个涡动频率下密封动力特性系数的求解[11]。
预旋是影响密封动力特性的重要因素,气流在进入密封时受到高速旋转的转子带动,不仅沿轴向流动,还有一定的周向速度分量。当转子涡动时,转子与密封之间的间隙在全周的分布不再相同,不均匀的圆周间隙使得气流对转子产生周向不平衡的作用力,继而促使转子做偏心运动,从而加剧了转子运行的不稳定性[12]。Benckert通过实验研究得到,密封进口处同转动方向的流动,会使密封产生不利于稳定的交叉刚度从而降低转子的稳定性[13]。近年来国内外学者采用CFD方法针对含预旋密封流场及其动力特性进行了一定的研究[14-16],Childs采用数值模拟与实验的方法,研究了逆旋栅对直迷宫密封动力特性的影响,结果表明逆旋栅可以有效提高密封稳定性[17]。孙丹等采用CFD方法研究了反旋流对直迷宫密封动力特性的影响[18]。陈尧兴等采用CFD数值方法研究了不同预旋比下密封腔室旋流强度、周向压力与转子动力特性的变化规律[19]。Corral和Vega提出了一种新型密封颤振综合模型,通过构建无因次参数Wcyc,来描述每个周期中流体对密封做功的正负,其包含了预旋、密封齿间隙、腔体几何形状、密封两端压力比、振动模态等因素对密封稳定性的影响,但仅适用于直迷宫密封[20-21]。国内外学者的研究主要集中于等间隙的迷宫密封形式,例如直齿密封。已有实验研究结果表明,台阶齿和直齿密封的性能具有区别,例如齿型结构参数相同时,台阶齿相比直齿的泄漏系数有所降低[22],同时,密封的几何因素如密封齿形和齿间空腔对密封流场也会产生影响[23]。在燃气轮机、压缩机系统中经常用到阶梯密封结构,但是目前关于进口预旋对阶梯齿型迷宫密封动力特性影响的相关研究还较少。
本文研究了不同预旋比的情况下阶梯型迷宫密封的动力特性。基于Murphy小位移涡动原理建立气流激振力-转子位移-转子速度的控制方程,采用CFD数值模拟方法对不同预旋比的全环密封流道进行计算,通过频域内求解控制方程得到了不同预旋情况的刚度和阻尼等特性参数,通过绘制压力云图、速度矢量图表征了密封内流场特性。研究结果可为阶梯型迷宫密封的动力学设计提供参考。
1 考虑预旋的密封动力特性计算方法
在压缩机中,气体经过叶轮后压力上升,压力差促使气流在叶轮和静子的间隙中回流泄漏,通过密封结构可以减少工质的回流泄漏,提升压缩机效率。在叶轮口位置处,常采用如图1a所示的阶梯型迷宫密封。
气流沿径向流入间隙,在到达密封前经历弯曲的流道而转为轴向流动。由于转子壁面对气流的黏性拖动,气体存在一定的周向速度分量,产生密封进口预旋如图1b所示。预旋对密封动力特性具有显著影响[13],定义进口处气流的周向速度分量Vt与进口处转子运行线速度Vr之比为预旋比
(1)
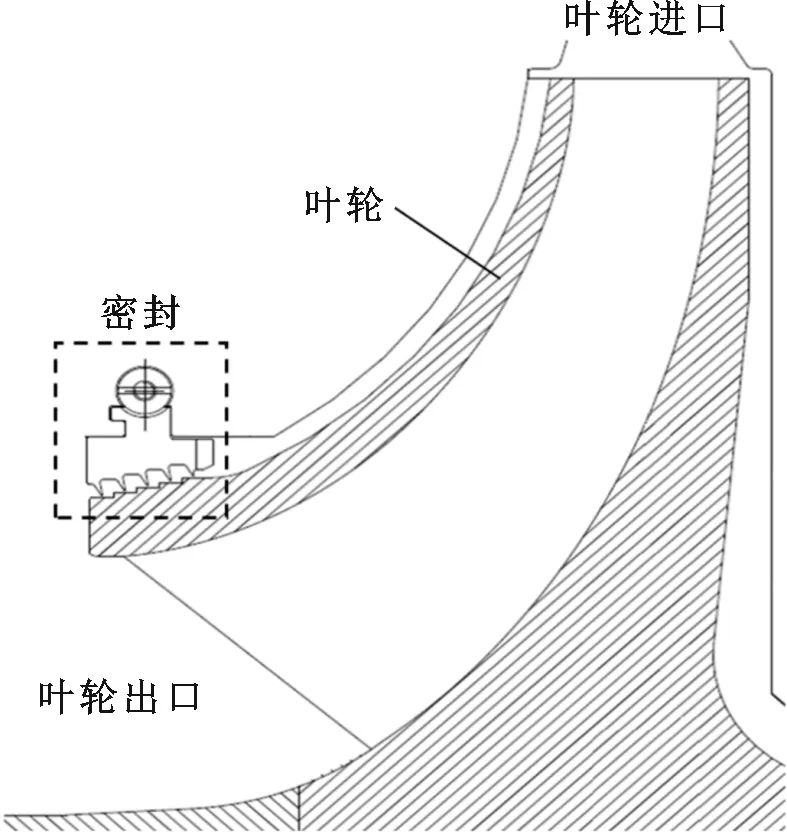
(a)阶梯型迷宫密封

(b)密封的进口预旋图1 阶梯型迷宫密封和进口预旋Fig.1 Step-shaped labyrinth seal and inlet pre-swirl
式中:n为转子转速;D为进口位置转子直径。
与传统直密封相比,阶梯密封的每个密封腔底面距轴心的距离不再相同,图2给出了阶梯型密封的截面示意图,在转子运行时,每个密封腔内底面的转子运动线速度也不相同。
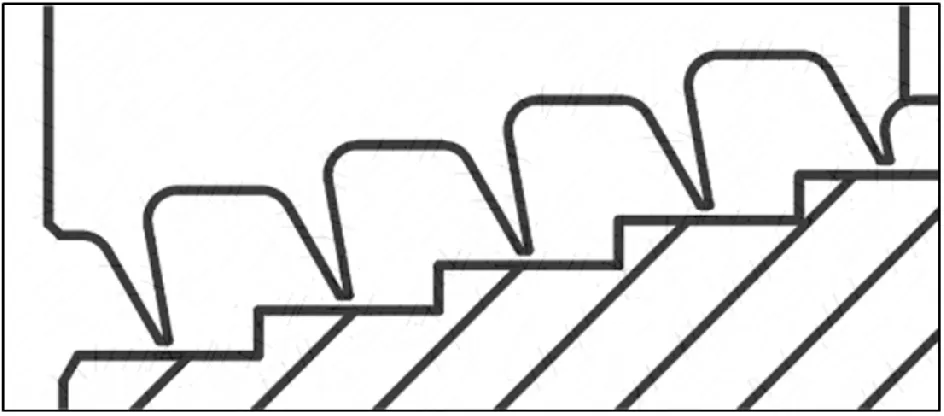
图2 阶梯型密封截面示意图Fig.2 A cross section of step-shaped labyrinth seal
对于阶梯密封,要考虑各密封腔的底面位置不同带来的转子表面运动速度差异。在转子发生涡动时,转子表面上某点的运动速度Vi等于涡动速度Vo与转子表面旋转线速度的矢量和。
(2)
式中:Di为不同阶梯位置对应的转子直径;ai为对应的单位切向量。
在密封-转子的整体结构中,当转子涡动时,根据Murphy小位移涡动原理[24]可得,密封气流激振力与转子位移及速度之间的控制方程为
(3)
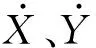
通过给定转子位移X、Y,采用CFX软件进行三维非定常CFD求解,得到气流激振力Fx、Fy。
密封气流激振力是在时域内的多频波动信号,其频率成分与涡动位移、涡动速度相同。为了求解各涡动频率下转子的动力特性系数,采用快速傅里叶变换(FFT),将位移、速度以及激振力等时域信号转化为频域信号,得到频域内激振力与位移的关系式为
-Ψyy=(Kyy+jΩCyy)Dyy+(Kyx+jΩCyx)Dyx
(4)
-Ψyx=(Kxx+jΩCxx)Dyx+(Kxy+jΩCxy)Dyy
(5)
-Ψxx=(Kxx+jΩCxx)Dxx+(Kxy+jΩCxy)Dxy
(6)
-Ψxy=(Kyy+jΩCyy)Dxy+(Kyx+jΩCyx)Dxx
(7)

令Hij=Kxx+jΩCxx为密封的阻抗特性系数,通过方程组式(4)~(7)联立求解,得到4个待求未知量Hij的值。根据实部和虚部的对应关系,可以得到密封刚度特性参数Kij和阻尼特性参数Cij
(8)
实际计算时,给出的转子位移X、Y必须能合理地描述多种因素共同影响下的转子运动。本研究采用多频椭圆涡动模型[25],认为转子的涡动由N种不同频率fi的椭圆涡动共同叠加而成,转子在多频涡动下的轴心运动方程为
(9)
按照多频椭圆涡动假设,转子轴心的运行轨迹将是各单一椭圆轨迹的叠加,选取N=10,a=1.5 μm,b=3 μm,各涡动频率fi以20 Hz为间隔,依次取20、40直至200 Hz。长轴为y方向的转子涡动轴心轨迹如图3所示。
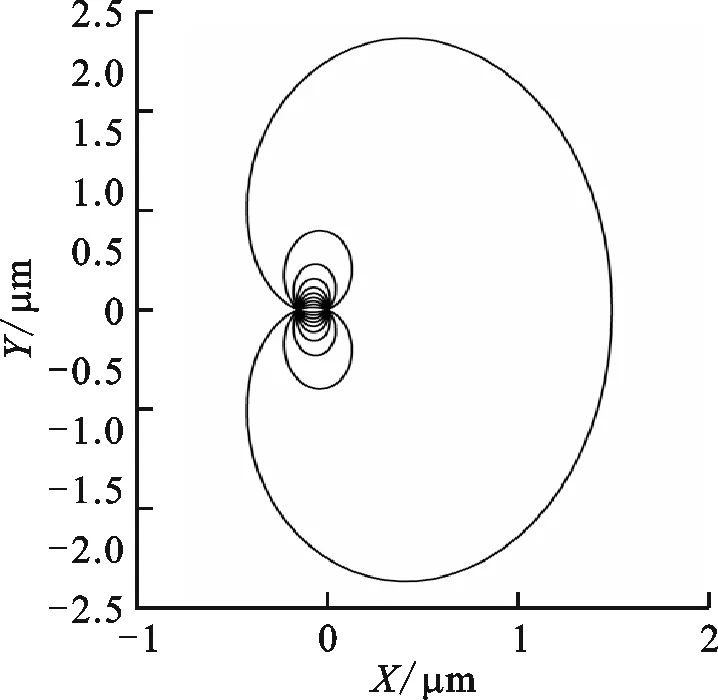
图3 转子涡动轴心轨迹Fig.3 Trajectory of rotor axial center under whirling motion
2 密封的结构参数
计算对象为某离心式管线压缩机第一级叶轮口处的阶梯型迷宫密封,其结构如图2所示。阶梯密封总长度为33 mm,密封齿数为5个,腔室深度为5 mm,腔室长度为6 mm,进口处密封齿顶与轴心的距离为208 mm,每隔一个阶梯齿,齿顶距轴心的距离减小1.5 mm。
流体工质为天然气,工质温度为21.5 ℃,在密封进口处总压为9.13 MPa,出口静压为7.39 MPa,转子的工作转速为6 000 r/min。在本研究中,计算了λ为0、0.255、0.516等工况。
由于进口气流的预旋,气流具有周向速度,需要考虑气体在各扇区之间流动,因此计算时采用全环模型。建立了密封流道的全环模型,并进行了非结构化网格的划分。对密封腔采用O型结合C型子块,为提高求解精度,射流区以及近壁面区域采用加密的网格,在节流间隙处布置20个节点,密封全环模型几何结构及网格划分如图4所示,总网格数为966.4万。
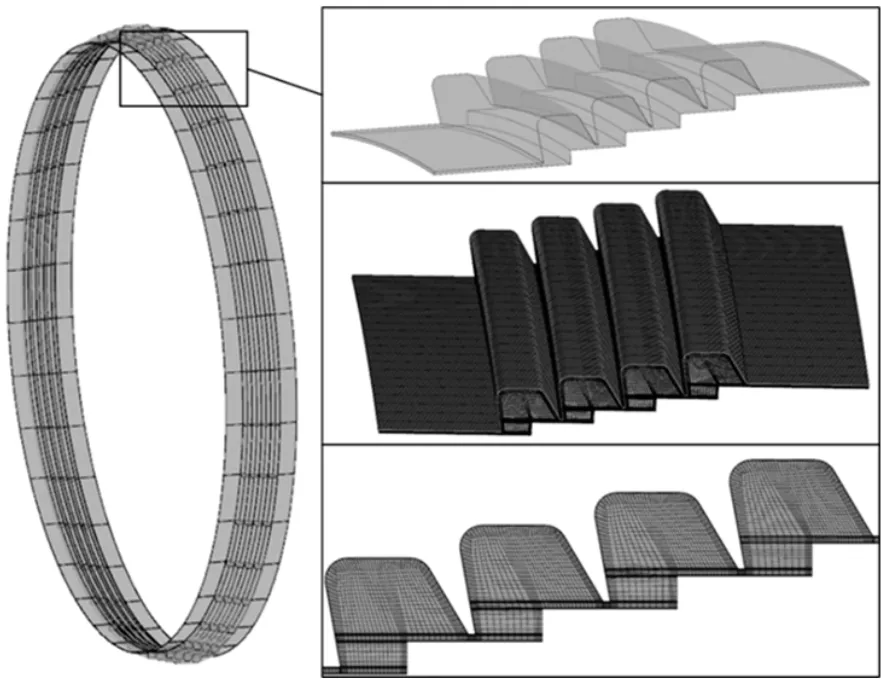
图4 密封全环模型几何结构及网格划分Fig.4 Whole ring model and meshing of the seal
3 动力特性计算结果及分析
针对密封腔的全环模型,采用定常计算收敛的结果作为非定常计算的初场进行瞬态计算,对转子施加多频椭圆涡动位移激励,如图5a所示。进口指定总压和总温,出口指定静压边界条件,固体壁面采用绝热无滑移边界条件,时间步长取为10-4s。以λ为0.516工况为例,通过CFD方法计算得到的气流激振力响应如图5b所示。

(a)涡动位移
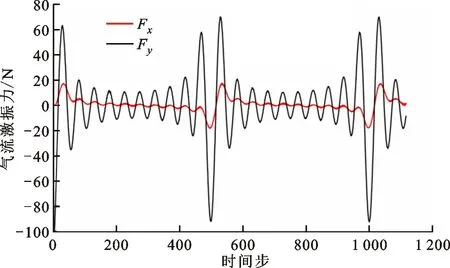
(b)气流激振力图5 转子涡动位移和气流激振力时域曲线Fig.5 Time-domain curves of rotor displacement and airflow induced force
由图5可以看出,多频椭圆涡动激励下,转子面的Y向涡动位移由多个频率叠加而成;受转子面涡动的影响,气流激振力呈现明显的周期性变化的特征。在幅值方面,涡动位移的变化引起的Y方向气流激振力较大,X方向气流激振力较小。
通过CFD方法计算得到气流激振力的时域响应后,通过密封动力特性的求解方法,对转子位移和气流激振力进行时频域变换,求解频域方程组,得到各涡动频率下转子密封动力特性系数如图6所示。
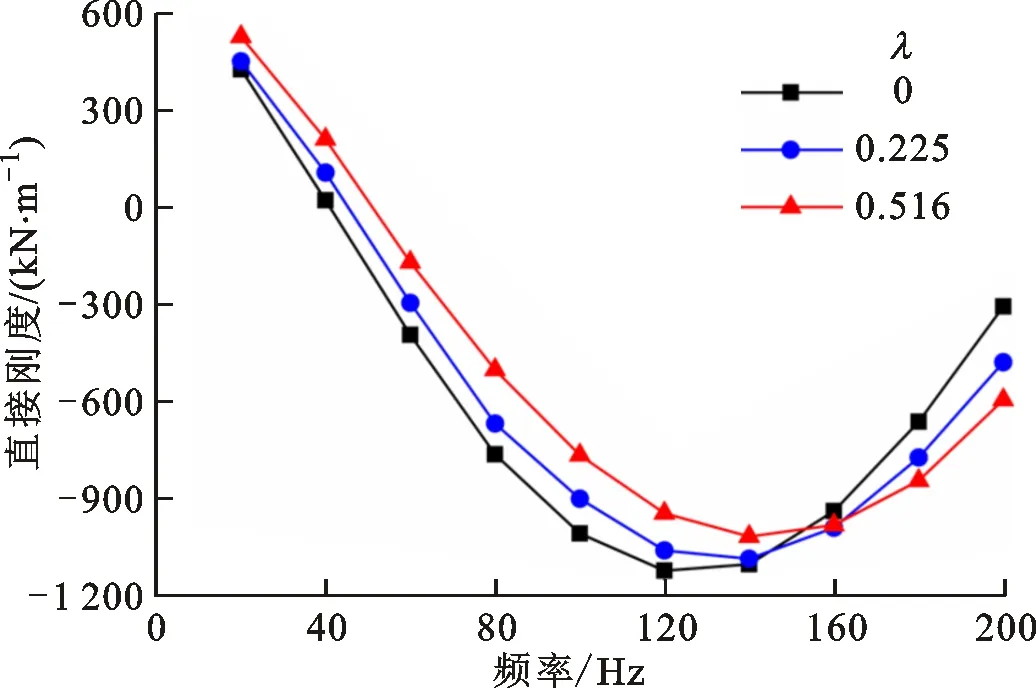
(a)直接刚度

(b)交叉刚度
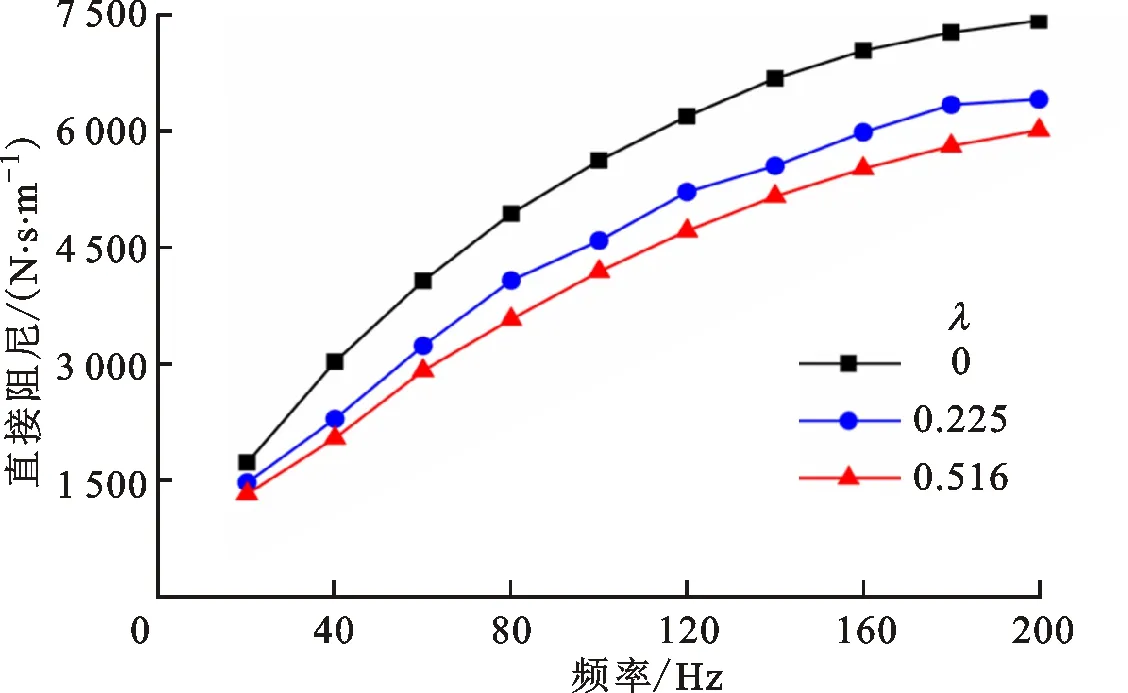
(c)直接阻尼
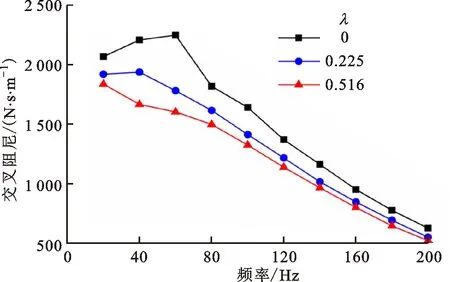
(d)交叉阻尼图6 各涡动频率下转子密封动力特性系数Fig.6 Dynamic characteristic coefficients of rotor at each vortex frequency
从图6可以看出,直接刚度随涡动频率先减小后增大,考虑预旋后,直接刚度在低频部分增大,高频部分减小;交叉刚度随涡动频率增加而增大;直接阻尼随涡动频率增加而增大,考虑预旋后直接阻尼减小;交叉阻尼随涡动频率整体呈现减小的趋势,考虑预旋后,交叉阻尼减小。
对于密封-转子系统,主要考虑交叉刚度和直接阻尼。交叉刚度是促使转子做非同步低频涡动的激振力来源,增大时转子稳定性降低,从图6b可以看出,进口预旋对交叉刚度影响不大。直接阻尼是低频涡动现象的抑制力,越大越有利于系统稳定,从图6c可以看出,预旋比为0.255时,直接阻尼相较于无预旋时平均减小16.9%,预旋比为0.516时,直接阻尼平均减小21.4%。可见,气流预旋明显降低了直接阻尼,对转子安全运行存在威胁。
通过密封流场压力及流速的分布,可以分析密封的流场特性。图7~9分别是预旋比为0.516工况时阶梯密封流道截面上的压力分布、流线及速度矢量图。

图7 密封流道截面压力分布Fig.7 Pressure distribution on the section of seal flow passage

图8 密封流道截面流线Fig.8 Streamlines on the section of seal flow passage
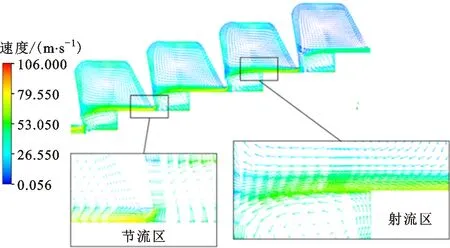
图9 密封流道截面速度矢量图Fig.9 Velocity vectors on the section of seal flow passage
由图7可以看出,阶梯密封流道中气体压力逐级递减,气流经过3个密封齿的压降分别为0.25、0.374和0.499 MPa,压降逐级增大。随节流次数的增加,气体流速增加,气流在3个密封齿顶的流速分别为79.5、88.36和106.0 m/s,射流区内流速明显高于涡流区;射流区的流体在冲击密封腔壁面后发生分离,在密封腔内形成一大一小两个涡团;两个涡团流动方向相反,大涡团沿顺时针方向流动,导致气体回转,小涡团沿逆时针方向流动,并在密封齿的顶部再次分流,一部分进入下一个密封腔,一部分则回转汇入小涡团中。
与直密封相比,阶梯密封由于密封齿阶梯式的排列,增加了主流道的复杂性,密封腔内的射流因冲击壁面向两边扩散,形成了气流旋涡,气流动能由于旋涡作用转化为热量,增加了流道内动能的耗散,使得密封效果更好。
4 结 论
建立了考虑进口预旋的阶梯型迷宫密封动力特性计算方法。计算了某阶梯型迷宫密封在不同预旋比工况的密封动力特性系数,数值仿真得到以下结论。
(1)随预旋比的增加,直接刚度在低频部分增大,在高频部分减小,交叉刚度几乎不变,直接阻尼和交叉阻尼均随预旋比增加而减小。
(2)预旋比为0.255时,直接阻尼相较于无预旋时平均减小了16.9%,预旋比为0.516时,直接阻尼平均减小了21.4%,气流预旋明显降低了直接阻尼,对转子安全运行存在威胁。
(3)λ为0.516时,气流经过3个密封齿的压降逐渐增加,分别为0.25、0.374和0.499 MPa,随着节流次数增加,密封齿顶的流速也逐渐增加,分别为79.5、88.36和106.0 m/s。
(4)由于密封齿阶梯式的排列增加了主流道的复杂性,阶梯密封的流道内存在节流区、射流区和涡流区;涡流区一大一小两个旋涡的存在,增加了流道内气流动能的耗散。
