(Ti/Zr/Hf/Sn/W)NbMoTaV高熵合金性能第一性原理计算分析方法
2022-03-15李雪洁孙琨陈诚杨龙龙杨经纬孙俊红
图1所示超高速无润滑测试平台(火箭橇实验平台)是一种大型、高精度地面动态模拟实验设备。在火箭橇高速地面实验过程中,滑靴轨道接触表面间由于无任何润滑剂、摩擦热的热效应、微观粗糙接触表面相互高速冲击等因素,造成滑靴轨道之间存在着严重的机械摩擦磨损现象,最终导致整个材料的宏观性能大幅度下降
。基于超高速火箭橇平台的发展需要,超高速实验中滑靴材料所面临的严酷工况要求其具有更加优异的高温性能,特别是高温耐磨性以及高温塑性韧性。目前广泛研究的镍基高温合金仍旧存在应用温度上的限制,而众所周知高熵合金(HEAs)具有很多优良的性能,是当前材料研究中的热门材料,其中能在高温下依旧展现极好的综合力学性能的难熔高熵合金(RHEAs)更加具备应用优势。

自2004年Yeh、Cantor等独立发表了多主元混合制备高熵合金的研究成果
以来,由于HEAs具备不同成分之间的高混合熵效应、一般具有稳定且结构简单的固溶体相、多元素合金化导致的晶格畸变效应而形成固溶强化等特性
,因此受到学者广泛关注。关于HEAs的研究多集中于实验研究。Du等观察了难熔高熵合金Al
(TiZrHfNb)
在高温高压真空中与Ti
AlNb扩散键合,使用扫描电镜分析了微观结构和元素分布,并通过纳米压痕和剪切测试评估了机械性能
。Xu等通过在NbMoTiVSi
难熔高熵合金添加硅化物研究了相组成、微观组织演变和力学性能,发现随着硅含量的增加,合金的屈服强度、极限强度显著增加。但是实验研究易受实验设备、操作技术和无法排除的偶然因素等限制,无法深入探究高熵合金性能变化微观机理
。
从孔子“礼”的发生机制来看,礼必须具有能指导主体实践的功能。前文提到,孔子之“礼”是在周礼实践基础上之改造再实践。礼的核心内容包含了对人伦关系的规定。孔子强调,仁是礼的核心内涵,所以礼的内容主要着眼于仁的约制规范和实践。孔子主要从以下两个方面进行对于礼的规制的:其一是处于特殊的身份、地位的道德实践主体拥有不同的道德实践义务与原则,其一是作为一般普遍意义上而言的道德实践主体又必须必须具有共同的行为准则。
基于密度泛函的第一性原理计算方法仅需要基本的物理参数即可进行与实验结果有相当程度一致性的计算,已经作为一种成熟的计算方法研究了HEAs的各种性能,相关研究成果也已经广泛发表在各类文献上,对从微观角度理解和设计预测HEAs起到了不可或缺的作用。例如Ge等基于第一性原理计算和准谐波德拜模型研究了四元合金AlMoTiV、CrMoTiV、MoNbTiV和三元合金CrMoTi、MoNbV、MoNbTi、MoTiV,在有限的温度下分析了温度变化和元素含量的改变对热性能和弹性模量的影响
;Zheng等基于第一性原理计算了70种不同元素的添加对VMoNbTaW弹性的影响
。
本文针对WNbMoTaV
硬度值高、高温压缩强度较高,但是断裂为解理脆性断裂、塑性较差这一问题,采用可以保证材料高强度的同时提高合金塑性变形能力,还能大幅度地降低合金密度的HCP稳定元素Ti、Zr、Hf
和含量较少时随着含量增加而使得合金的强度和塑性同时提高的Sn
来替换易氧化、塑性较差的W来探究合金元素对难熔高熵性能的影响机制。基于第一性原理方法对(Ti/Zr/Hf/Sn)NbMoTaV合金进行相关计算模拟,与WNbMoTaV合金进行了对比,分析了其相稳定性、结构稳定性和弹性力学性质,可为新一代高超声速火箭橇滑靴材料研发提供一定的参考。
1 第一性原理计算方法
高熵合金原子尺寸差异参数为
本文采用合金理论自动化工具包ATAT
软件的特定准随机结构
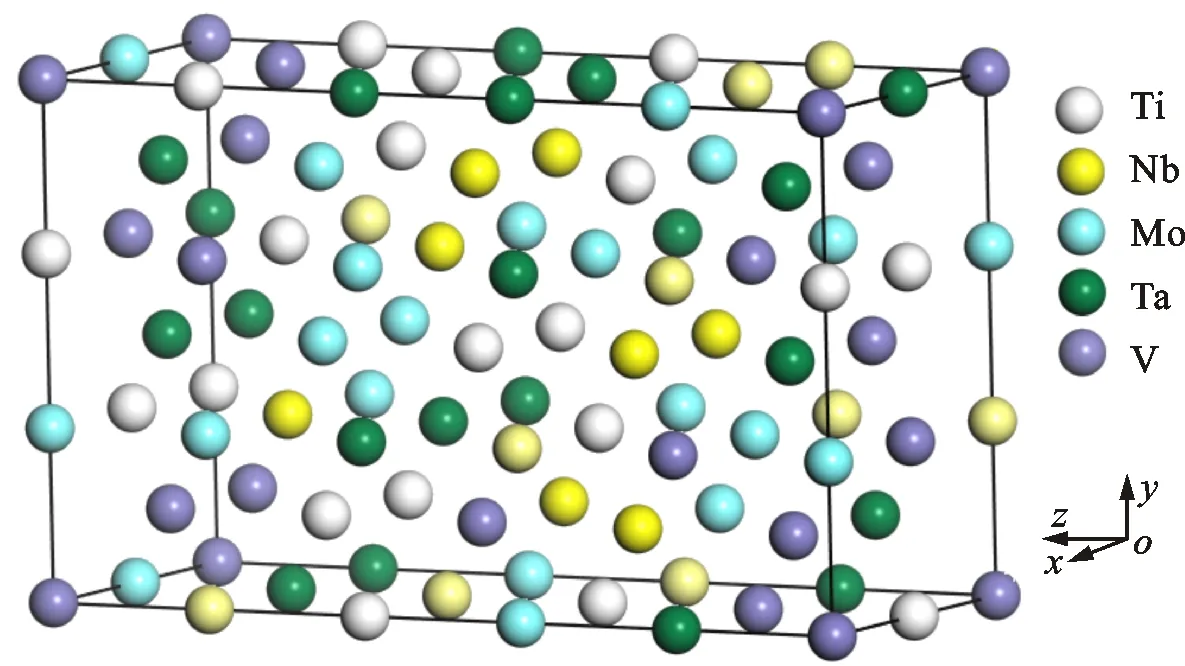
方法构建无序单相HEAs固溶体结构。本文中所有HEAs固溶体第一性原理计算模型均为2×3×5的60个原子的体心立方(BCC)超胞结构,TiNbMoTaV高熵合金晶胞结构如图2所示,(Zr/Hf/Sn/W)NbMoTaV合金与其类似。
2 高熵合金性能计算结果与讨论
2.1 (Ti/Zr/Hf/Sn/W)NbMoTaV高熵合金相形 成分析
根据已有文献可知,有相当一部分的HEAs并不是单一的无序固溶体相,可能还有金属间化合物相、纳米相以及非晶相等存在,而HEAs中的相组成对其性能有着至关重要的影响,进而影响其应用范围,因此本文首先对(Ti/Zr/Hf/Sn/W)NbMoTaV高熵合金相形成进行理论计算分析,为后续第一性原理模拟分析提供建模信息。
本文从以下7个参数对所研究的高熵合金相结构进行分析评判。
高熵合金原子半径差的均方差为
在木结构建筑施工中,施工企业应组织相关管理人员对施工现场加强管理,对施工管理机制进行完善,并根据该制度来开展施工管理工作。由于施工管理涉及的方面较多,包括施工人员管理、施工设备与材料管理等,通过施工现场管理制度的建立确保工程施工有据可循,对施工人员行为加以规范,对于施工过程中各种材料的具体施工情况,检查人员要进行记录,避免因为材料质量不达标而造成施工问题。为提高施工人工作积极性,施工企业还应建立奖惩制度,使施工人员工作积极性得到提升,确保安全管理的有效落实,为建筑工程施工的进行做出贡献。
“学起于思,思源于疑。”在数学教学中,教师要善于启发学生产生疑问,鼓励和引导学生大胆质疑问题,对学生的创新质疑要给予充分的肯定,保护学生质疑问难的积极性,使学生敢于表达自己的见解。此外,也要根据儿童的的好奇、好问、求知欲望强等特性,努力为学生创造宽松、自由、开放式的课堂氛围,激发学生创新的勇气,让学生敢想、敢说、敢问为什么。如学生掌握了“圆柱体的表面积求法后,有位学生问:求长方体和正方体的表面积时,能不能也用侧面积加上两个底面的面积来求它们的表面积。像这样的问题提得好,教师应给予肯定,给予鼓励。

(1)

式中:
为合金中第
个主元的价电子浓度。

(2)
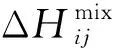
高熵合金混合熵为
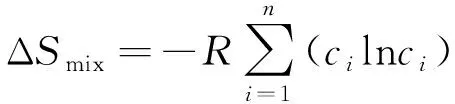
(3)
式中:
表示摩尔气体常数,
=8
314 4 J/(K·mol)。
经过统计两组患者患病诱因,发现观察组患者吸烟、糖尿病、高血压及高血压等高危因素明显发生率高于对照组,两组差异具有统计学意义(P<0.05),见表1。
计算了3个模型得到的碎片最终速度与数值模拟得到的碎片最终速度之比。3个模型计算得到的装药比比值误差的比较如图6所示。可以看出,模型2确实明显偏离数值模拟结果,而模型1和模型3在跳跃变化的区段(装药比为0.657%~0.792%),理论模型与数值计算相比没有明显的差别。但是随着装药比的增大,模型1和模型3的结果与数值模拟结果之间的偏差越来越大。相对而言,模型3是基于动量守恒的3阶段计算模型,其结果与数值模拟结果最为接近,δ在10%以内。说明,对于小装药比爆炸驱动双层壳体的情况,单纯基于Gurney公式的直接应用要谨慎,发展两段驱动理论模型进行碎片速度的估算是有必要的。
高熵合金价电子浓度为
1.1.1 发病症状稻瘟病在水稻全生育期中都可发病,按发生部位和表现的症状可以分为苗瘟、叶瘟、叶节瘟、节瘟、穗颈瘟和谷粒瘟。
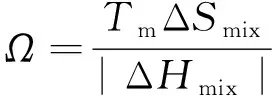
(4)
剪切模量
取Hill近似,即Voigt近似和Reuss近似的平均值
高熵合金电负性差为
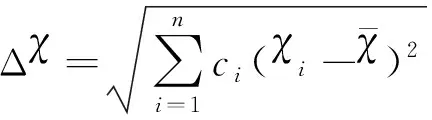
(5)

发达生产事业,无论是资本主义者,或是社会主义者,都是绝对承认的 要想为中国无产阶级谋幸福而除去一切悲痛,首先就要使他们获得生活必需的资料。要使他们获得生活必需的资料,首先就要开发生产事业。所以发达生产事业的一件事,无论是资本主义者,或是社会主义者,都是绝对承认的,只不过生产方法不同罢了!
本文所有第一性原理计算均使用基于密度泛函理论和平面波方法的维也纳大学Hafner小组开发的进行电子结构计算和量子力学-分子动力学模拟软件包(VASP)程序
完成,采用离子和电子间的相互作用、采用投影缀加平面波(PAW)方法
处理和电子间的交换关联作用、采用广义梯度近似(GGA)下的一种近似的能量泛函(PBE)
描述;计算平面波函数展开的动能截断选择400 eV,
点在进行HEAs结构优化和弹性常数计算时取值为5×5×5,进行单原子能量计算时采用
点,并采用金属体系常用的一阶Methfessel-Paxton smearing方法设置波函数的部分占有数,
取值为0.2。在各项静态计算前,均采用共轭梯度法进行结构优化,收敛条件为:总能量变化小于1.0×10
eV,每个原子上的力小于0.01 eV/Å。以上所有参数均经过收敛性测试。

(6)
本节研究以第一性原理计算为主,先对在(Ti/Zr/Hf/Sn/W)NbMoTaV合金进行结构驰豫,获得能量最低的稳定超胞结构模型。在此基础上,通过应力-应变法对其弹性常数矩阵
进行计算,其中立方晶系有独立的弹性常数
、
和
。分别计算本文5种HEAs相应的高熵合金的体积模量
、弹性模量
、剪切模量
(取Voigt和Reuss的近似平均值)、泊松比
、Pugh比
、硬度
、柯西压力
-
、Zener各向异性系数
和Chung-Buessem各向异性系数
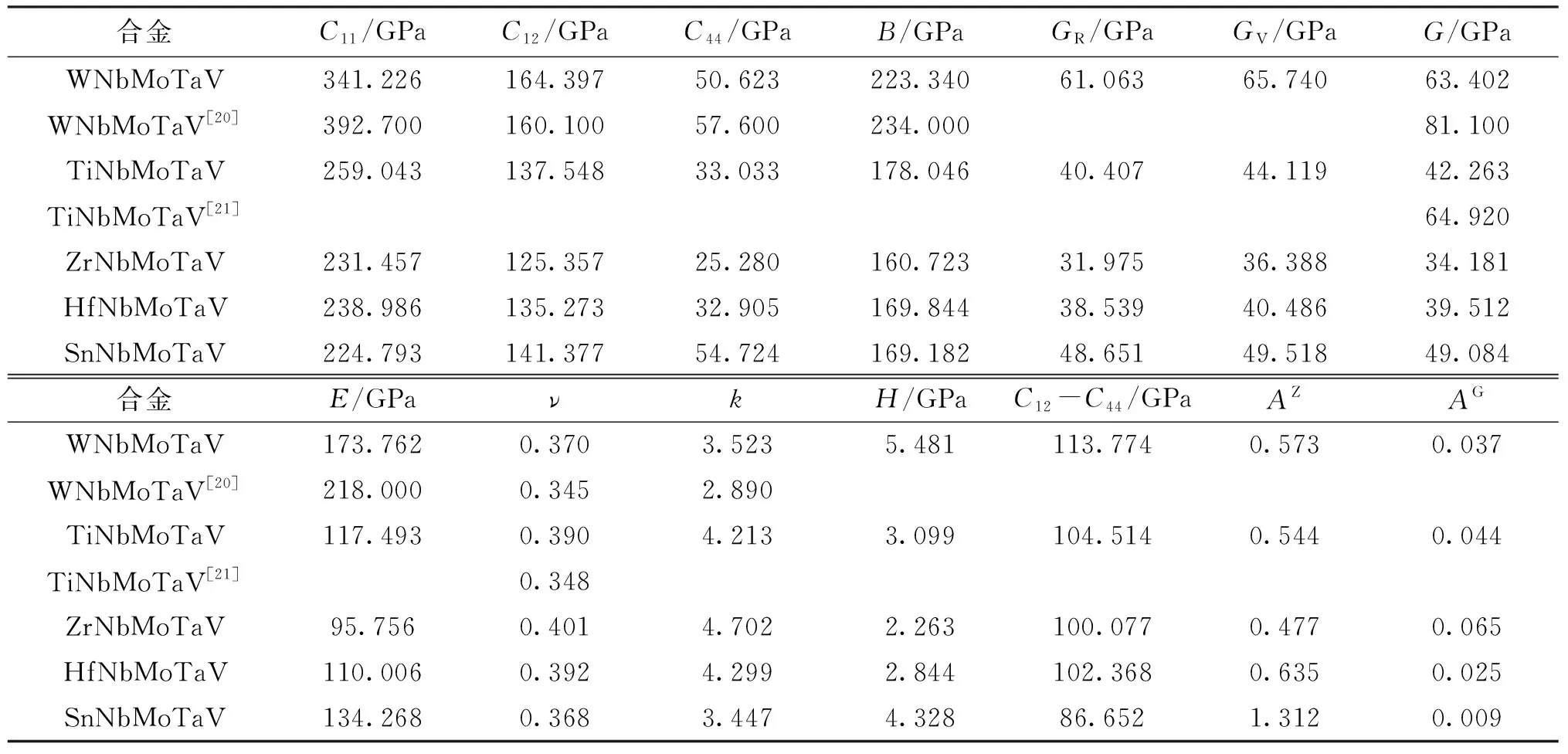
,合金弹性性质的计算数据及其他文献对比结果见表3。
高熵合金熵焓比为

(7)
高熵合金混合焓为
本文合金的相形成规律计算结果如表1所示。当合金同时满足
<6
5%,混合焓Δ
在-15~5 kJ/mol之间,混合熵Δ
在12~17.5 J/(K·mol)之间且
≥1
1,可以形成无序固溶体相;另外,电负性差越小越有利于多组元固溶高熵合金形成
;
<1
175
时也可判断其形成固溶体相。此外,还可通过价电子浓度判断出固溶体的具体结构:当
≤6
87,仅存BCC相;当6
87≤
≤8,BCC相和面心立方(FCC)相同时存在;当
≥8,仅存在FCC相
。
从知识、技能、态度三个维度KMO值分别为0.854、0.857、0.873,都大于0.8,表明在结构效度方面较好,研究数据可以用于进一步地分析。
根据表1的数据,5种HEAs计算出的
范围为3.6%~4.9%,均小于6.5%;计算出的Δ
范围为-4.64~0.32 kJ/mol,均包含在-15~5 kJ/mol之间;Δ
的计算结果都是13.386 J/(K·mol),在12~17.5 J/(K·mol)的范围内;
的计算结果范围为8
542~97
243,都远大于1
1;
的计算结果范围为1
105~1
150,都小于1
175。以上计算结果说明这5种HEAs都为无序固溶体相。
的计算结果范围是5~5
4,都小于6
87,可得知(Ti/Zr/Hf/Sn/W)NbMoTaV合金都为单一的体心立方结构,与文献[9]中WNbMoTaV合金为单一体心立方结构的实验结果一致。
2.2 (Ti/Zr/Hf/Sn/W)NbMoTaV高熵合金结构 稳定性分析
通过2.1节计算分析发现(Ti/Zr/Hf/Sn/W)NbMoTaV合金都为单一的体心立方结构。为进一步确定这些HEAs结构的稳定性,本节分别构建BCC和FCC结构高熵合金第一性原理计算模型进行计算。
内聚能
被定义为将晶体分解成单个自由原子的能量,计算公式如下

(8)
式中:
表示晶胞中的原子数;
表示体系总能;
表示五元高熵合金单个元素原子弛豫后的总能量;
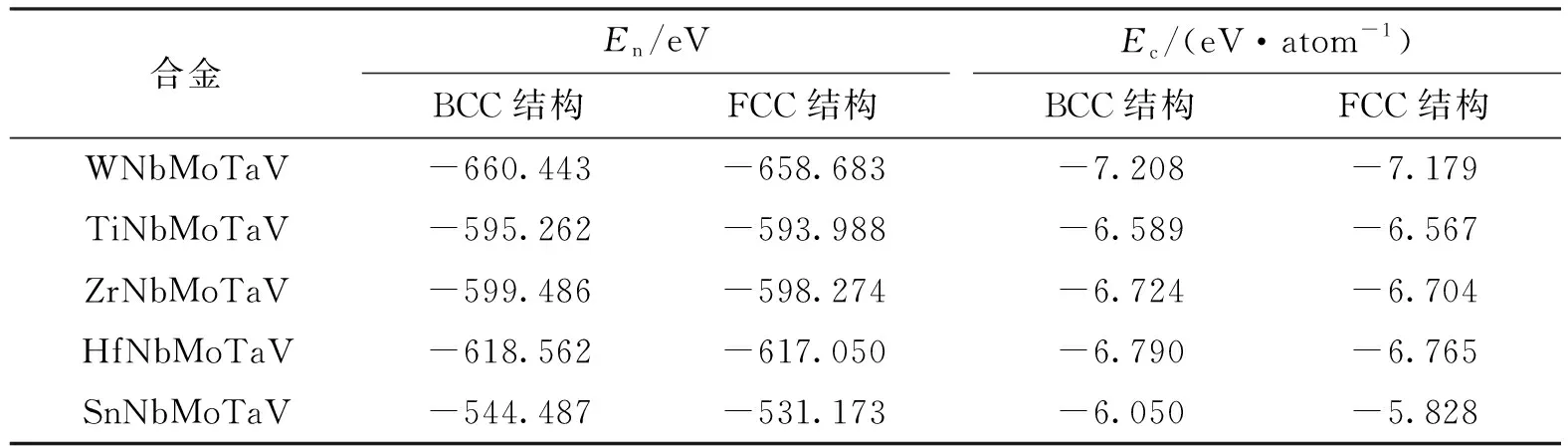
表示各元素原子数。合金能量和内聚能计算结果见表2。
从表2的数据可知,5种HEAs的BCC结构能量均小于FCC结构,计算出的BCC结构的
也均小于FCC结构的
,因为较低的内聚能意味着更好的结构稳定性,所以可证实(Ti/Zr/Hf/Sn/W)NbMoTaV合金都为单一的体心立方结构,与相形成规律的计算结果一致。

2.3 (Ti/Zr/Hf/Sn/W)NbMoTaV高熵合金弹性 性质分析
式中:
、
分别为合金中最大和最小的原子半径。
建筑安全管理标准体系要做到科学有效运行需要从上至下,对现场施工的每一个环节都加强关注,从而促进标准化建设的有效实施,但是现阶段大多数项目因节约人工成本,施工现场的组织机构仍不够健全或没有完善,无法做到全面监控,因此要按照安全管理标准化体系来指导和监督每一个环节的施工,建立健全组织机构非常重要。
For the saturated regime, as shown in Fig. 3, the distribution of the depletion layer was made in five regions, and therefore:

(9)
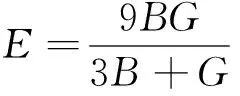
(10)
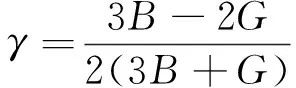
(11)
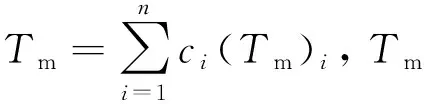
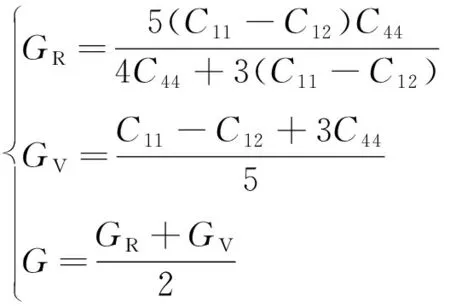
(12)
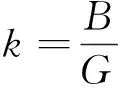
(13)
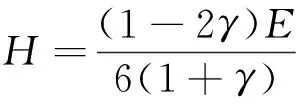
(14)
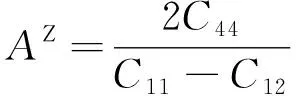
(15)
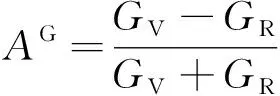
(16)
将本文计算结果和其他文献对比,可以得出所有误差均在35%以下,可能是由于建立的模型大小不同,
、
和截断能的设置不同导致的计算结果的偏差。
首先,可以根据表3中弹性常数的计算结果判断立方结构的力学稳定性,判据
为

(17)
由表3可以看出,(Ti/Zr/Hf/Sn/W)NbMoTaV合金均满足力学稳定性判据,说明这5种材料在0 GPa下都是力学稳定的,与2
1和2
2节的结论一致。其次,文献[23]中提出当合金满足
>1
75且
>0
26,同时柯西压力
-
>0,合金则表现为塑性,且柯西压力越大塑性越好,否则就为脆性材料;表3数据中的5种材料均满足
>1
75,
>0
26,柯西压力
-
数值大于0的条件,所以这5种材料都有良好的内在塑性。其中
和
最大的是ZrNbMoTaV合金,最小的是SnNbMoTaV合金;柯西压力
-
最大的是WNbMoTaV合金,最小的是SnNbMoTaV合金。最后,Zener各向异性系数
为1表示材料为各向同性,否则为各向异性,并且值越大,各向异性越强。Chung-Buessem各向异性系数
为0表示材料为剪切各向同性,否则为剪切各向异性,并且值越大,剪切各向同性越强
。由表3可以看出,(Ti/Zr/Hf/Sn/W)NbMoTaV合金的
都不为1且
也不为0,说明5种HEAs均表现为各向异性,其中SnNbMoTaV合金的各向异性最高,剪切各向异性最低。
根据以上数据可得出,将五元高熵合金中的W替换成Ti、Zr、Hf导致材料的强度明显下降,塑性虽有提升但数值有限,材料的各向异性略有下降,但剪切各向异性有所增加;而将W替换成Sn导致材料的强度和塑性都略有下降,各向异性增加,剪切各向异性明显降低。
2.4 态密度分析
为了探究材料结构稳定性的内在机制,计算了如图3所示的(Ti/Zr/Hf/Sn/W)NbMoTaV合金与组成元素的态密度,描述了电子在不同能量状态下的数量比。图3是WNbMoTaV、TiNbMoTaV、ZrNbMoTaV、HfNbMoTaV和SnNbMoTaV合金的态密度图,均在费米能级
处连续,则合金均表现为金属键特征;能级主要集中在-10~2 eV;各元素对总态密度的贡献几乎均等,Mo和V的贡献量与其他元素相比稍大一些;有明显的赝能隙存在,而且各元素基本都在-4~1 eV范围内形成明显的杂化,说明合金中存在各元素之间的共价键。
事业单位要重视预算绩效管理在单位的重要程度,务必将预算管理贯穿到单位管理的始终,建立贯穿预算编制、执行、监督全过程的预算绩效管理体系。预算的编制需要多个部门相互配合,单位管理者和各部门人员都应参与其中。预算目标设定要与事业发展规划和年度工作计划紧密衔接,确定预算重点投向,满足未来事业发展的需要。
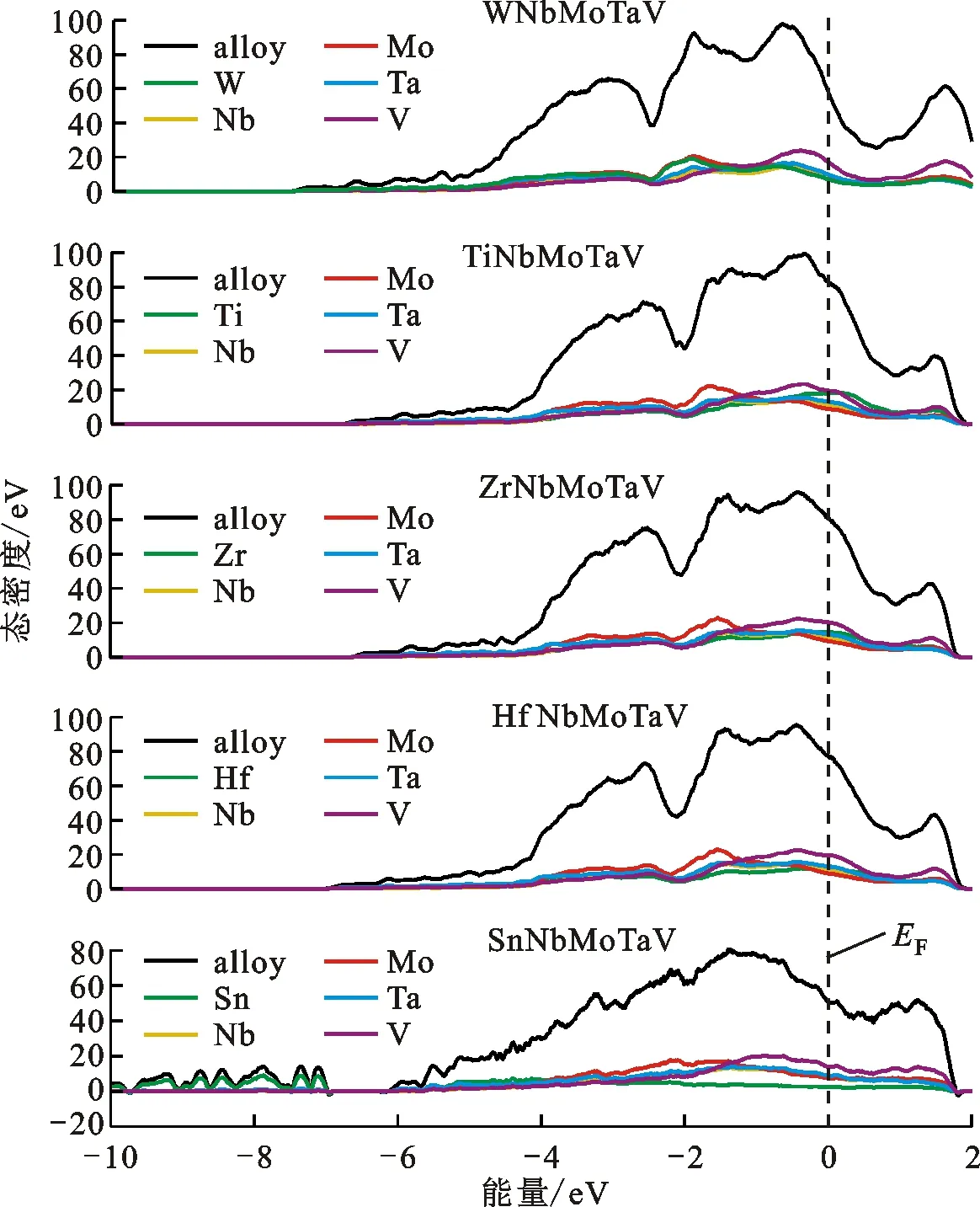
由图3可以看出,将W替换成Ti、Zr、Hf后,成键峰的高度有轻微下降,尤其在
的右侧,即(Ti/Zr/Hf)NbMoTaV合金的高能能带与WNbMoTaV合金相比较少,主要集中在低能成键区上;
附近的成键峰变窄,并向高能反键区方向有所偏移,且
处的态密度增大,使得整个体系的成键变得不稳定,说明(Ti/Zr/Hf)NbMoTaV合金与WNbMoTaV合金相比共价性变弱而结合键能是影响弹性模量的主要因素,两者对应关系密切,结合键能越大,原子之间距离的移动所需的外力就越大,即弹性模量越大。其中在结合键中共价键的键能仅次于最强的离子键
,结合2.3节弹性性能的计算,得知Ti、Zr和Hf的替换降低了原本材料的弹性性能。由图3可以看出,能级分布中多出了-10~-7 eV的部分,且此部分完全由Sn贡献;成键峰的高度下降表现在
的左侧,
附近的成键峰变窄,使得整个体系的成键变得不稳定,SnNbMoTaV合金与WNbMoTaV合金相比共价性变弱;同样结合2.3节弹性性能的计算得知,Sn的替换也降低了原本材料的弹性性能。
3 结 论
本文使用理论公式计算了(Ti/Zr/Hf/Sn/W)NbMoTaV合金的相形成规律和结构稳定性,基于第一性原理计算方法研究了这5种材料的弹性性质,分析了其态密度计算结果,主要结论如下。
(1)(Ti/Zr/Hf/Sn/W)NbMoTaV合金都是单一的体心立方结构。
(2)(Ti/Zr/Hf)NbMoTaV合金与WNbMoTaV合金相比,弹性常数、体模量
、弹性模量
、剪切模量
、硬度
,柯西压力(
-
),Zener各向异性系数
数值均下降,而SnNbMoTaV合金的
数值却有所上升;前3种合金的泊松比
,Pugh比
、Chung-Buessem各向异性系数
数值上升,而SnNbMoTaV合金的这3项数值都是下降的。说明(Ti/Zr/Hf)NbMoTaV与WNbMoTaV合金相比,材料的强度有所下降但塑形有所提升;而SnNbMoTaV合金与WNbMoTaV合金相比,材料的强度和塑性都不如后者,但抗剪切性能较好。
(3)(Ti/Zr/Hf/Sn)NbMoTaV与WNbMoTaV合金相比,整个体系成键的稳定性下降,共价性变弱,说明Ti、Zr、Hf、Sn的替换降低了原本材料的弹性性能。
:
[1]王玮华, 谢发勤, 吴向清, 等. 火箭橇滑块超声速、大载荷摩擦磨损失效机理 [J]. 材料导报, 2020, 34(16): 16136-16139.
WANG Weihua, XIE Faqin, WU Xiangqing, et al. Investigation on friction and wear failure mechanism of rocket sled slide at supersonic and under high load [J]. Materials Reports, 2020, 34(16): 16136-16139.
[2]YEH J W, CHEN S K, LIN S J, et al. Nanostructured high-entropy alloys with multiple principal elements: novel alloy design concepts and outcomes [J]. Advanced Engineering Materials, 2004, 6(5): 299-303.
[3]CANTOR B, CHANG I T H, KNIGHT P, et al. Microstructural development in equiatomic multicomponent alloys [J]. Materials Science and Engineering: A, 2004, 375/376/377: 213-218.
[4]KANG B, LEE J, RYU H J, et al. Ultra-high strength WNbMoTaV high-entropy alloys with fine grain structure fabricated by powder metallurgical process [J]. Materials Science and Engineering: A, 2018, 712: 616-624.
[5]DU Y J, XIONG J T, JIN F, et al. Microstructure evolution and mechanical properties of diffusion bonding Al
(TiZrHfNb)
refractory high entropy alloy to Ti
AlNb alloy [J]. Materials Science and Engineering: A, 2021, 802: 140610.
[6]XU Qin, CHEN Dezhi, TAN Chongyang, et al. NbMoTiVSi
refractory high entropy alloys strengthened by forming BCC phase and silicide eutectic structure [J]. Journal of Materials Science & Technology, 2021, 60: 1-7.
[7]GE Huijuan, TIAN Fuyang, WANG Yang. Elastic and thermal properties of refractory high-entropy alloys from first-principles calculations [J]. Computational Materials Science, 2017, 128: 185-190.
[8]ZHENG Shumin, WANG Shaoqing. First-principles design of refractory high entropy alloy VMoNbTaW [J]. Entropy, 2018, 20(12): 965.
[9]刘学峰. 难熔高熵合金的制备及其组织性能研究 [D]. 北京: 北京理工大学, 2015: 1-63.
[10]孙博, 夏铭, 张志彬, 等. 难熔高熵合金性能调控与增材制造 [J]. 材料工程, 2020, 48(10): 1-16.
SUN Bo, XIA Ming, ZHANG Zhibin, et al. Property tuning and additive manufacturing of refractory high-entropy alloys [J]. Journal of Materials Engineering, 2020, 48(10): 1-16.
[11]张勇, 陈明彪, 杨潇, 等. 先进高熵合金技术 [M]. 北京: 化学工业出版社, 2019: 1-226.
[12]KRESSE G, HAFNER J. Ab initio molecular dynamics for liquid metals [J]. Journal of Non-Crystalline Solids, 1993, 47(1): 558-561.
[13]BLÖCHL P E. Projector augmented-wave method [J]. Physical Review: B, 1994, 50(24): 17953-17979.
[14]PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple [J]. Physical Review Letters, 1996, 77(18): 3865-3868.
[15]VAN DE WALLE A, ASTA M, CEDER G. The alloy theoretic automated toolkit: a user guide [J]. Calphad, 2002, 26(4): 539-553.
[16]VAN DE WALLE A, CEDER G. Automating first-principles phase diagram calculations [J]. Journal of Phase Equilibria, 2002, 23(4): 348.
[17]VAN DE WALLE A, TIWARY P, DE JONG M, et al. Efficient stochastic generation of special quasirandom structures [J]. Calphad, 2013, 42: 13-18.
[18]熊青云, 申江, 田付阳. 理论研究VTiTaNbAl
高熵合金的结构与弹性力学性质 [J]. 原子与分子物理学报, 2016, 33(5): 901-906.
XIONG Qingyun, SHEN Jiang, TIAN Fuyang. Theoretical study of structures and elastic mechanics of VTiTaNbAl
high-entropy alloys [J]. Journal of Atomic and Molecular Physics, 2016, 33(5): 901-906.
[19]GAO M C, NIU Changning, JIANG Chao, et al. Applications of special quasi-random structures to high-entropy alloys [M]∥High-Entropy Alloys: Fundamentals and Applications. Berlin, Germany: Springer International Publishing, 2016: 333-368.
[20]ZHENG Shumin, FENG Wenqiang, WANG Shaoqing. Elastic properties of high entropy alloys by MaxEnt approach [J]. Computational Materials Science, 2018, 142: 332-337.
[21]LIU Qing, WANG Guofeng, SUI Xiaochong, et al. Ultra-fine grain Ti
VNbMoTa refractory high-entropy alloys with superior mechanical properties fabricated by powder metallurgy [J]. Journal of Alloys and Compounds, 2021, 865: 158592.
[22]GRIMVALL G. Thermophysical properties of materials [M]. Amsterdam, Netherlands: Elsevier, 1999: 46-48.
[23]张辉, 李兴国, 郭古青, 等. FeAl
NiCrMn系高熵合金力学性能的第一性原理计算 [J]. 特种铸造及有色合金, 2020, 40(10): 1172-1176.
ZHANG Hui, LI Xingguo, GUO Guqing, et al. First-principle calculation on mechanical properties of FeAl
NiCrMn high-entropy alloys [J]. Special Casting & Nonferrous Alloys, 2020, 40(10): 1172-1176.
[24]文志勤. 镍铝多熵合金的结构及物理性能的第一性原理研究 [D]. 太原: 中北大学, 2019: 55-56
[25]石德珂. 材料科学基础 [M]. 2版. 北京: 机械工业出版社, 2003: 26.
