基于深度学习的公共充电桩故障预测模型

吴 丹，王 俊，许 燕

（1.国网上海市电力公司，上海 200122；2.上海电力实业有限公司，上海 200025）

现阶段充电桩的功能逐渐完善，其设计结构也越来越复杂，受多种因素的影响后，难免发生各种故障，降低了自身功能。如果运维部门没有及时发现和检修就可能导致严重的事故发生，造成经济损失，甚至危及到人身安全。因此，应确保充电桩的有效运行，消除潜在故障，公共充电桩故障预测则成为电动汽车行业在发展过程中极为重要的技术之一。

近几年，对充电桩故障的分析研究较多，林越等人[1]进行了一种基于隐生灭过程模型的充电桩故障诊断研究。对状态转移只在相邻状态间发生的情况进行分析，完成在特定规则下隐生灭过程模型的构建，通过生灭过程的局部平衡方程组给出了充电桩在发生故障时的稳态分布，并且对稳态分布物理意义一一解释。金勇等人[2]提出一种基于故障字典法的交流充电桩故障检测方法。该方法结合充电桩中电器元件的主要特征，对交流充电桩发生故障的主要模型进行分析，提取出充电桩内的主回路相关电量特征，采用故障字典法完成故障的监测全过程。

但是上述方法只能对现有故障进行及时诊断，无法对未发生的故障进行预测，不能做到防患于未然，因此，文中构建一种基于深度学习的公共充电桩故障预测模型。

1 充电桩故障预测模型

深度学习作为机器学习的一个分支，其实质为多层人工神经网络，主要通过模拟人脑建立用于分析学习的神经网络以实现对数据的解释。深度学习网络的构架较多，例如卷积神经网络[3]、循环神经网络[4]等，而文中以更适用于充电桩故障预测的深度受限玻尔兹曼机为构建模型的基础深度学习网络，实现对充电桩故障预测模型的建立。

1.1 深度受限玻尔兹曼机训练

受限玻尔兹曼机（Restricted Boltzmann Machine，RBM）为一种无向图网络模型，包含卷积层、隐层和可视层3 层网络。其基本模型如图1 所示。

图1 受限玻尔兹曼机模型

RBM 网络输入是Nm×Nm二值单元，隐层中含括K个子隐层，各个子隐层大小为Nh×Nh。引入权值共享思想，即在每个相同的子隐层中的单元共享同一个卷积核，每个卷积核即为一个滤波器。若滤波器的大小为Nw×Nw，则各个子隐层共享一个偏置b。对于所有可视层，若共享偏置为c，则RBM 的能量函数可以表示为：

式（1）中，v为可视层，vij为连接i可视层单元与j隐层单元的值；为第i个可视层单元与第k个子隐层内的j单元的值，bk表示k子隐层的偏置。

可视层的输入值为0-1 二值矩阵，隐层单元也为二值单元，因此为求得隐层单元的具体数值，可采用Gibbs 采样法[5]。采样的实现具体过程如下，首先固定可视层v的数值，计算出隐层h的后验概率，固定隐层的值后，计算可视层v的后验概率。反复进行以上操作，直至收敛。采样的数学表达式可以表示为：

式（2）中，σ()· 为sigmiod 函数。在可视层v确定的条件下，进行隐层的采样操作，同理，在隐层固定后，完成可视层的采样。获得各个单元后验概率后，将后验概率和均匀分布抽样后获得的概率进行比较以激活各层单元。

为便于概率处理，将每个输入变量归一化至[0,1]间，对RBM进行进一步优化，其能量函数可以表示为：

则可视层神经元的条件概率可以表示为：

式（4）中，N()· 是均值为μ、标准差为σ的正态分布概率密度，隐藏神经元的条件概率为：

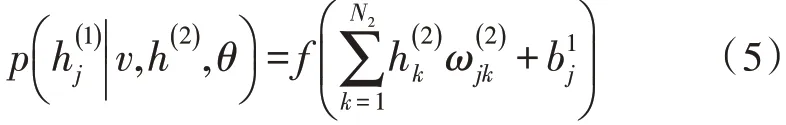
在Gibbs 采样法的基础上，加入逐层预训练过程[6-8]。该过程是从下至上对每一层的RBM 进行学习，使用训练后的权重θ={ω1,ω2,…,ωl} 构造DBM。

预训练算法如下：

1）首先使用CD 算法对第一层的RBM 进行训练，并且在训练过程中要保持从下自上的权重2ω1为从上到下权重ω1的两倍。

2）固定2ω1值不变，通过采样获得h1，随后以h1为输入数据对第二层RBM 进行训练。

3）固定2ω2值不变，通过采样获得h2，并以其为输入数据对下一层进行训练。

4）重复以上操作，直至训练到l-1 层。

5）采用CD 算法对最上层的RBM 进行训练，在此过程中始终保持由下自上的权重ω1。

6）最后使用权重{ω1,ω2,…,ωl} 构造DBM。

1.2 预测模型构建

在深度受限玻尔兹曼机的深度学习网络基础上，使用极限梯度提升决策树法构建预测模型。主要思想是将多棵决策树的模型进行组合，从多维度分析信息，提高模型的准确率[9]。给定含有n个样本、m个特征的样本集，表示为D={xi,yi}，其中x、y表示特征向量与因变量。训练时，给定一个目标函数：

式（6）中，w表示模型内待估计函数，l(w)表示损失函数，Ω(w)表示正则化项，该操作的主要作用为控制模型复杂程度。

损失函数的数学表达式为：

式（7）中，表示第t轮模型预测值，=0,fk(xi)表示回归决策树。

因此，目标函数的形式可以重新表示为：

采用泰勒二次展开[10-12]，形式如下：

定义：

获得近似目标函数，为了减少计算量，去除常数项，目标函数的形式可以表示为：

随后将决策树分为树结构部分q与叶节点分数部分ω，则每一个决策树可以表示为：

对决策树的复杂程度进行重新定义，如下：

在新定义条件下，新形式的目标函数可以表示为：

此目标中包含了T个独立单变量的二次函数。将其进行变量求导即可获得最优值如下：

此时即可获得最佳决策树：

式（16）中，γ为新子节点加入后增加的复杂度。当Gain＜0 时，XGBoost 停止分裂，此时参数γ正在此处处理复杂性。分裂点为Gain最大值时被认定为最优分裂。

充电桩发生故障可能由多种因素导致而成，其中最为常见的是外部环境和运维频率。因此文中从以上两个方面结合深度学习给出故障预测模型，发生故障和运维频率之间的预测模型如下：

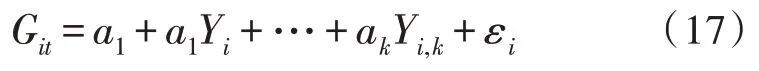
式（17）中，Yi,j,j=1,2,…,k为影响第i个桩的j个运维因素，其中包括运维部门处理的及时率Dit、充电桩的硬件质量CZit、维修及时率CWit、充电区停电时长WCit，定义以上模型的前半部分为运维频率对故障发生的影响指数[13-15]，则可得：

外部环境的影响主要反映在天气对充电桩发生故障的影响，其模型如下：

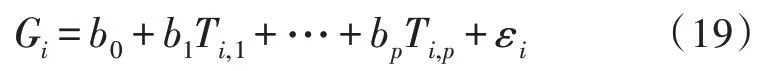
式（19）中，Ti,j(j=1,2,…,p)为影响i桩的j种环境因素，其中包括风向风力、雨雪、温度等，在多种环境条件下进行充电桩故障预测[16]。

最后将环境影响指数与运维影响指数融合给出综合预测模型，以反映环境与运维频率对充电桩发生故障的总效应，可以表示为：

通过综合影响模型即可实现充电桩故障预测。

2 仿真实验

以某一地区的充电桩作为实验样本，采集共一个月时间的样本数据。在此期间存在充电桩出现故障情况，为验证文中预测模型的有效性，实验提供了数据，删除无效数据后，选择采集所得数据中的100个样本数据，将其分为训练集和测试集，其中80 个为训练集、20 个为测试集。与文献[1]、文献[2]方法进行对比分析，3 种模型所得的ROC 曲线(Receiver Operating Characteristic curve，受试者工作特征曲线)如图2 所示。

图2 不同方法的测试集ROC曲线

从图2 中可以看出，文中方法曲线更靠近左上方，表明文中模型的预测能力更强，从定量数值角度分析，文献[1]、文献[2]和文中方法的测试结果如表1所示。从表1 中可以看出，3 种方法的AUC（Area Under Curve，ROC 曲线下方的面积大小）数值分别为0.887、0.872、0.864，测 试集的准 确率为89.21%、93.46%、97.78%，进一步证明了文中方法的准确率更高，实际应用价值更高。

表1 不同方法测试结果

3 结束语

故障预测能够为充电桩的日常运维提供数据基础[17]，因此文中以公共充电桩较为常见的故障原因为理论基础，结合深度学习法提出了一种基于深度学习的公共充电桩故障预测模型，并且通过实验证明了所提方法具有较高的预测准确性，获得了阶段性研究进展，但是还存在一些问题需要进一步探索。