基于改进模拟退火算法的PCB 电子元器件热优化布置研究
2022-03-15吴沐羿李先允王书征
吴沐羿,李先允,王书征
(南京工程学院电力工程学院,江苏南京 211167)
“摩尔定律”指出集成电路板上晶体管的数量每过18 个月便会增加一倍。芯片计算能力呈现指数级增长的同时,相关问题也亟待解决[1]:电子设备晶体管数量急剧增加,导致集成电路板出现漏电现象甚至过热击穿,影响使用效率和寿命。
自1970 年以来,国内外学者对PCB 板上电子元件的散热优化技术有大量研究:文献[2]基于模拟退火算法实现了若干个PCB 元器件的阵列优化,并且用Icepak 进行仿真验证。文献[3]以150 kW 直流充电桩为研究对象,借助仿真软件分析内部流体场和温度场,通过正交试验法对散热器结构进行优化。文献[4]采用遗传算法对光伏并网逆变器的元器件位置进行优化,对散热器的选型进行对比并进行仿真验证。
综合参考上述已有研究,文中提出一种PCB 电子元器件优化布置的热设计方法。根据PCB 尺寸大小,建立元器件位置的二维阵列式布置模型,用改进的模拟退火优化算法对二维阵列式布置模型与元器件选位顺序分别进行优化,且用ANSYS Icepak 热仿真软件进行验证。
1 电子元件布置模型
根据相关文献,在此类问题的研究过程中,PCB板上各电子元器件的布置问题属于平面优化布置问题。为方便研究的进行,需要建立PCB 板上功率元器件的模型,实现数学模型的搭建[5-8]。PCB 板与功率元器件的热学模型均定义为矩形,如图1 所示。搭建二维阵列式布置模型,在矩形PCB(500 mm×480 mm)上均匀分布五行四列(共计20 个)矩形位置,以放置电子元件,并按从左下到右上的顺序由1~20 依次编号。为实现程序编写,将PCB 板上功率元器件的排列方式定义为解空间X,解空间X的第k个元素对应该位置上放置的元器件的编号,如:假设当前PCB 板上放置20 个电子元件,则PCB 板上电子元件布置的解的形式为X={x1,x2,…,x20},其中,x1,x2,…,x20各自对应某电子元件的编号。向量形式的解X则对应元件的布置方案。文中所述的20 个电子元件中,1~5 号的发热功率为3 W,6~10 号的发热功率为5 W,11~20 号的发热功率为8 W。

图1 二维阵列式布置模型示意图
2 模拟退火算法改进
2.1 算法改进思路
模拟退火算法是一种基于迭代求解策略的随机寻优算法[9-11],最早由Metropolis N 等人于1953 年提出。其思想源于固体退火原理,从某一个较高初始温度出发,在不断降温的过程中,从解空间里随机寻找目标函数的全局最优解以实现优化。模拟退火算法的主体流程可以简单概括为如下步骤[12-14]:
Step1 规定新解生成的规律或函数,确定目标函数,并且生成一个初始解以实现后续迭代;
Step2 计算新解与旧解的目标函数差值,并且将两个解的值对于原数学模型的优劣进行对比评价;
Step3 判断新解是否被接受,通常判断的依据是Metropolis 准则;
Step4 将上一个步骤判断完毕后的解作为下一次迭代的解;
Step5 判断是否达成终止条件或迭代次数。若是,则结束算法并得出最终解;若否,则继续Step2 进行迭代。
该文的研究目的是实现PCB 板上功率元器件的散热优化,使用Matlab 软件进行算法程序的编写,并对模拟退火算法进行如下改进设计:
文中的优化过程分为两次:二维阵列式布置模型的优化以及在此优化基础上进行的元器件选位优化。二维阵列式布置模型的优化方法如下:通过模拟退火算法对上文所述的20 个矩形位置各自沿着x或y方向进行任意距离的正向或反向移动,得出该方案下的目标函数值,并且多次迭代寻找最优阵列模型;元器件选位优化方法如下:由二维阵列式布置模型优化完毕后,在最优阵列模型中寻找元器件选位的最优方案。文中的优化布置实施过程如图2 所示。

图2 优化布置实施过程
2.2 目标函数与接受准则
为寻找最佳散热布置方案,算法的目标函数需要准确体现不同距离与功率元器件之间的温度影响。差分法、有限元法、有限容积法都可以用于电子元器件表面温度的计算,但由于计算过程繁琐,并不适合用作温度评价函数。现选取一阶热设计公式[4],在该公式基础上进行相应修改后作为算法的温度评价函数,即算法的目标函数。该热设计公式的拟合多项式如下:

式(1)是元器件自身温度评价公式,其中,Pi为元器件i的功率;Pmax为元器件最大功率。
式(2)是其他元器件贡献温度评价公式,其中,Dji为元器件j到元器件i的距离;Ri为元器件i的封装半径。
则总体温度评价函数如式(3)所示:

二维阵列式布置模型优化的新解生成准则:随机抽取某矩形位置并确定方向及距离,这使得阵列模型的结果有多种可能。
元器件选位优化的新解生成准则:采用二变法,即对于某一迭代下的解空间X={x1,x2,…,xa,…,xb,…,xn},通过对两个随机数a、b的生成,将两个位置的元器件进行位置互换,得到新解X’={x1,x2,…,xb,…,xa,…,xn},新解生成方法的示意图如图3 所示。

图3 新解生成方法的示意图
模拟退火算法对于新解的接受与否采用Metropolis 准则,即以式(4)作为依据:

式(4)中,p为接受新解的概率;Ei、Ej分别是算法迭代过程中的第i代状态和第j代状态,并且i=j+1;K为Boltzmann 常数,是涉及温度及能量的物理常数;T为算法每一次迭代后的温度值。
3 热仿真准备流程
该文借助目前主流的热分析软件Icepak 进行仿真。Icepak 使用计算流体力学(Computational Fluid Dynamics,CFD)软件里精度较高的Fluent 求解器进行运算,借助ANSYS 建模软件可以准确搭建相关模型[15-16]。
3.1 搭建仿真模型
针对文中涉及的仿真模型,在基于其几何封装的基础上自建模型,借助软件自带的模块进行仿真模型搭建。
模型需要对求解区域进行定义,以“Cabinet”模块作为求解区域,模拟电子产品的实体外壳;PCB 板作为发热模块,借助方腔“Enclosure”模块实现与电子产品其他部分的隔热;模型的进出风口均采用滤网“Grille”模块;散热器采用“Heatsink”模块,其类型以及翅片参数都会影响散热效果;电子元器件采用“Source”热源模块建立,大型三维元器件采用“Block”建立,各模块需要具体设置其属性参数。
3.2 网格划分及求解设置
对所搭建的模型进行网格划分是热仿真的重要步骤,网格划分质量的优劣直接影响求解精度以及收敛与否。Icepak 提供3 种网格划分类型——Mesher-HD 网格、非结构化网格、结构化网格。文中选取非结构化网格,其可对规则的几何体进行贴体划分,与文中仿真模型相匹配。
在对模型划分完网格后,还需对所求解进行如下设置:
环境温度默认为20 ℃,计算域流体设定为空气,并且各类参数均为默认数值(比热容、热导率、压强);设置为湍流Zero equation 模型;设置重力加速度g方向并保持默认数值,海拔保持默认数值;忽略辐射换热;迭代步数设置为20 次。
4 仿真并分析
为验证文中所述的PCB 电子元器件优化布置方法的可行性,用软件Matlab 编写程序、Icepak 进行仿真,并与传统PCB 板热布局优化方法进行对比。
根据传统PCB 板散热优化方法,借助Matlab 优化程序对模型的元器件布置进行优化,得到传统优化后的布置方案,如图4 所示。将其布置模型搭建后,进行热仿真,为避免不必要的系统误差,网格划分及求解设置与上文相同,仿真结果如图5 所示。
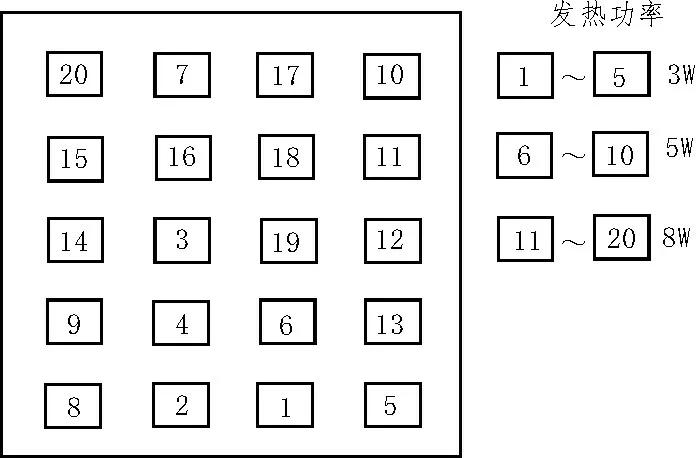
图4 传统优化后的布置方案

图5 传统优化仿真结果图
由图5可以看出,用传统散热优化方法优化后,PCB板上最高温度为49.931 4 ℃,最低温度为19.999 3 ℃,最大温差为29.932 1 ℃。
在此基础上用文中所述方法进行优化。首先进行二维阵列式布置模型的优化,通过Matlab 软件实现模拟退火算法寻优。为防止迭代次数过多或者陷入局部最优,经过多次仿真测试,确定算法迭代次数为100 次。如图6 所示,进行大约70 次迭代后,温度评价函数值实现了相对稳定。选取该结果下的二维阵列式布置方案,并搭建新的模型,二维阵列式模型优化后的布置方案如图7 所示。二维阵列式模型优化仿真结果如图8 所示。

图6 模拟退火算法迭代结果图

图7 二维阵列式模型优化后的布置方案

图8 二维阵列式模型优化仿真结果
由图8 可以看出,进行了二维阵列式布置模型的优化之后,元器件之间的距离相对变远,使得局部温度过高的现象有所缓和,并且高温区域的分布更加匀称。PCB 板上最高温度为47.716 0 ℃,最低温度为19.282 6 ℃,最大温差为28.433 4 ℃。
再进行元器件选位优化,借助Matlab 软件实现算法寻优。考虑到目标函数为热设计的拟合多项式,与实际物理规律具有一定误差,在多次仿真测试后选定迭代次数为20。迭代优化后,元器件的选位优化后的布置方案如图9 所示。并且对模型的功率进行调整,其仿真结果如图10 所示。
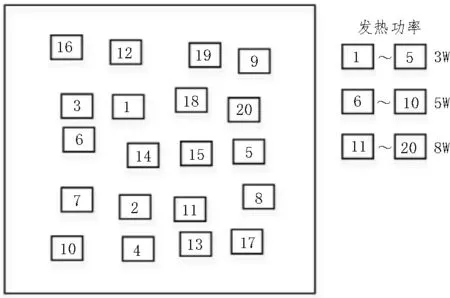
图9 选位优化后的布置方案
由图10 可以看出,进行了元器件选位优化之后,密集的8 W 元器件变得分散,原本高温分布区域的形状被改变,并且高温面积有明显缩小。等温线分布均匀,温度变化趋缓。PCB 板上的最高温度为46.837 9 ℃,最低温度为19.583 9 ℃,最大温差为27.254 0 ℃。

图10 选位优化仿真结果图
表1 是3 次仿真温度结果的汇总,结合仿真图不难看出,进行优化之后PCB 板最高温度下降,虽然最低温度相较第一步的优化有所升高,但总体而言,高温面积得到有效地减小。
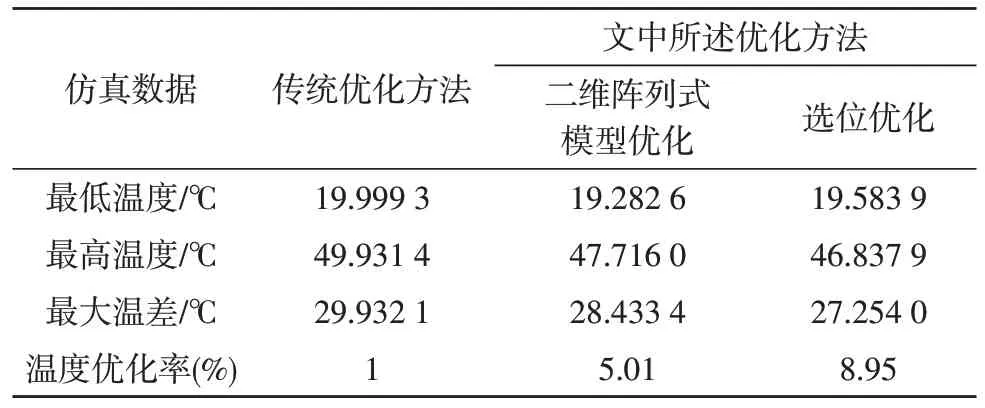
表1 仿真温度汇总表
5 结论
文中在PCB 散热优化方法的研究基础上,提出一种基于改进模拟退火算法的PCB 电子元器件优化布置方法,该方法能较灵活地优化PCB 板上元器件的散热。仿真结果表明,该方法经过两个步骤的优化后,使PCB 的温度比传统散热优化方法低3.09 ℃,优化率达8.95%,对散热的优化有一定的效果。
