基于模糊集理论的电网工程数据智能分析与评价方法

方 明，胡 龙

（广东电网有限责任公司广州供电局，广东广州 510600）

电网工程是指电力系统的发、输、配、变环节的建设工程[1-4]。在智能电网建设过程中，电网公司对电网工程项目的管理粗犷、形式单一，急需向智能高效、精益化的电网工程项目管理的方向转变[5-6]。

电网工程的可行性研究、初设、施工图等各阶段蕴含丰富的数据信息。电网公司掌握了丰富的电网工程项目技经数据，但未深入挖掘数据的价值[7-9]。如何深层次挖掘数据价值，提升电网工程造价分析和预测水平，提高电网公司投资决策能力是有待研究的重要方向。因此，文中基于电网工程投资造价智能评估分析系统，结合模糊C均值聚类（Fuzzy C-Means，FCM）与最小二乘支持向量机（Least Squares Support Vector Machine，LSSVM）算法，开展电网工程数据智能分析与评价方法研究。

1 系统架构

电网工程投资造价智能评估分析系统架构如图1 所示。其主要包括首页展示、项目管理、辅助评审、评审意见&质量评分、统计分析、造价控制指标测算、定额管理、造价分析、资源管理、现场辅助评审工具等共10 个模块，部分模块实现的主要功能如下。

图1 电网工程投资造价评估分析系统架构

1）首页展示。实现未评审和已归档主/配网项目的汇总统计及情况展示，展示维度包括横向与纵向维度，横向维度为可研、初设和施工图预算；纵向维度为不同工程类型、不同项目类型或不同项目版本等。

2）项目管理。对主/配网项目进行分类管理，包括可研、初设、预算等阶段，实现项目数据同步、智能检测、列表/详情展示、资料归档等功能，并帮助专家实现便捷的检索浏览。

3）辅助评审。提供未评审项目的展示列表和链接接口，自动根据评审资料及评审规则完成合规性的对比检查，统计评审结果数据并提供便捷查询。

2 电网工程数据智能分析与评价

基于电网工程投资造价评估分析系统，该文开展了电网工程数据的智能分析与评价方法研究。将系统平台的项目工程数据作为输入，采用FCM 对大量电网工程数据进行聚类；然后将聚类后的结果作为LSSVM 进行回归分析，实现电网工程的造价预估。文中所提基于FCM 与LSSVM 的电网工程数据智能分析和评价方法步骤如图2 所示。

图2 数据智能分析与评价方法

2.1 模糊C均值聚类方法

模糊集理论在聚类分析中的应用较为广泛，其中模糊C 均值聚类使用方便、收敛迅速，能够适应高维度、数据量大的场景[10-11]。

FCM 的核心思想是：首先随机选取若干个数据作为初始聚类中心；然后所有的数据样本均具有与聚类中心相关的模糊隶属度；最终以最小化所有数据样本到聚类中心的距离与模糊隶属度的综合值为目标，不断进行迭代，更新聚类中心。当达到最大迭代次数或满足精度要求时，结束迭代，输出最优的聚类中心。

式中，X为数据样本矩阵，其规格为n×m，其每一行为一个数据样本，共有n个数据样本，每个数据样本共有m个特征值。

FCM 方法将样本总数为n的数据集分为c类，假设c个聚类中心为：

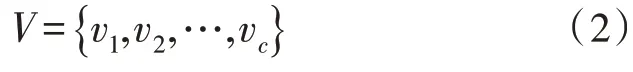
式中，第i个聚类中心为：

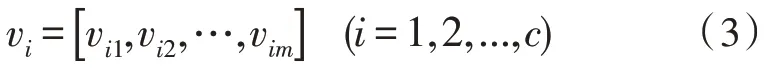
在FCM 中，对于任意数据样本xk，其并不是严格地属于某一分类，而是具有一定的隶属度值属于某一聚类中心代表的分类，该隶属度值满足以下关系：

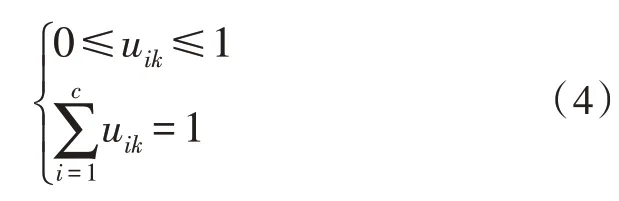
式中，uik为k个数据样本属于i个分类的隶属度。

迭代过程中的目标函数为：

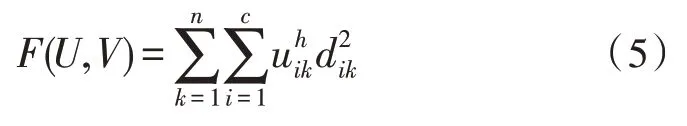
式中，U=(uik)c×n表示隶属度矩阵，dik为k个数据样本与i个分类的聚类中心欧式距离，F(U,V)表征所有数据样本到聚类中心的平方距离加权和，权重系数是k个数据样本属于i个分类的隶属度h次方。

dik的计算方式如下：

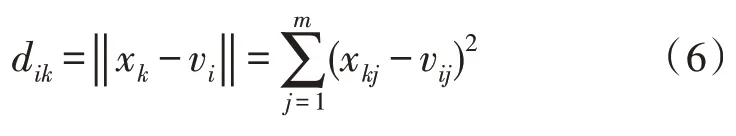
式中，‖ ‖· 表示二范数运算；xkj为第k个数据样本的第j个特征值；vij为第i个聚类中心的第j个特征值。

FCM 聚类的基本思路是求取U、V，使得式（6）中F(U,V)取最小值，其具体实现流程如图3 所示，主要步骤如下：

图3 模糊C均值聚类算法流程

1）输入FCM 算法参数，包括聚类中心个数c，最大迭代次数Lmax，幂指数h，最小精度ε。

3）根据下式计算第l次迭代的聚类中心V(l)：

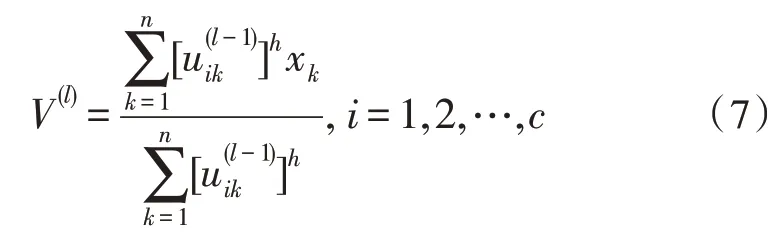
4）更新第l次迭代的隶属度矩阵U(l)，并计算出第l次迭代的目标函数值J(l)：

5）判断是否满足精度要求或达到最大迭代次数，即|J(l)-J(l-1)|＜ε或l＞Lmax。若是，则停止迭代；否则，令l=l+1，转至步骤3）。

经过FCM 的迭代计算，可以得到满足精度要求的隶属度矩阵和聚类中心，并使得目标函数值达到最小。进一步根据每个数据样本属于某类的隶属度大小，将数据样本归类于隶属度值最大的类，即当时，数据样本xk归属于第j类。

2.2 最小二乘支持向量机

对于数据(x1,y1),(x2,y2),…,(xl,yl)，通过非线性映射：φ(·)将数据样本映射到高维特征空间，并寻找最优决策函数y(x)=wφ(x)+b，从而实现将非线性拟合函数转换为高维空间的线性拟合函数[12-14]。

最小二乘支持向量机的目标是优化误差的二次项，优化问题为：

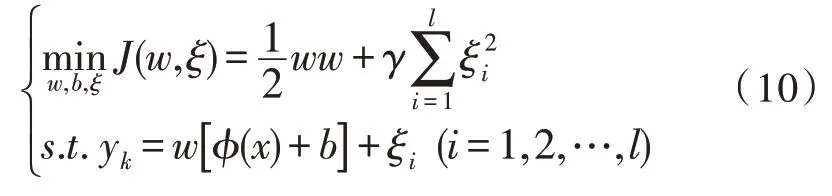
其中，γ为惩罚因子；ξi为松弛因子。

用Lagrange 法求解原优化问题转化[15-16]：

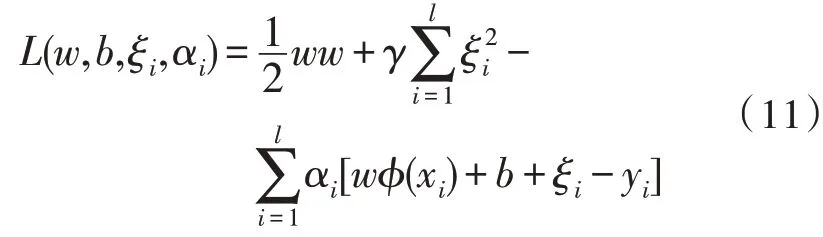
其中，αi为拉格朗日乘子。

L分别对变量w、b、ξk、αk求偏导，并令其等于0，得到下式：

消除上式中的w和ξi可得到：

采用核函数代替高维空间的内积计算：

通过最小二乘法求取α、b，从而得到基于最小二乘向量机的回归分析结果：

3 算例分析

为验证该文所提方法的正确性和有效性，采用电网工程投资造价评估分析系统的数据。电网工程数据共计413 条，来源于南方电网某供电局。以架空线路工程为例，影响其造价的主要因素如表1 所示。

表1 架空线路造价影响因素

3.1 FCM聚类评价

为评估FCM 聚类的效果，以Xie-Beni 指数作为有效性指标，其计算方法如下：

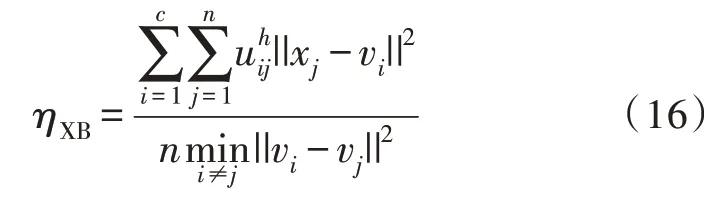
ηXB的取值越小，FCM 聚类效果越好。

将电网工程数据集作为FCM 输入，令聚类数c在2～14 范围内变化，得到Xie-Beni 指数变化情况，如图4 所示。由此可知，当聚类数c=6 时，Xie-Beni指数最小，因此最佳聚类数为6。

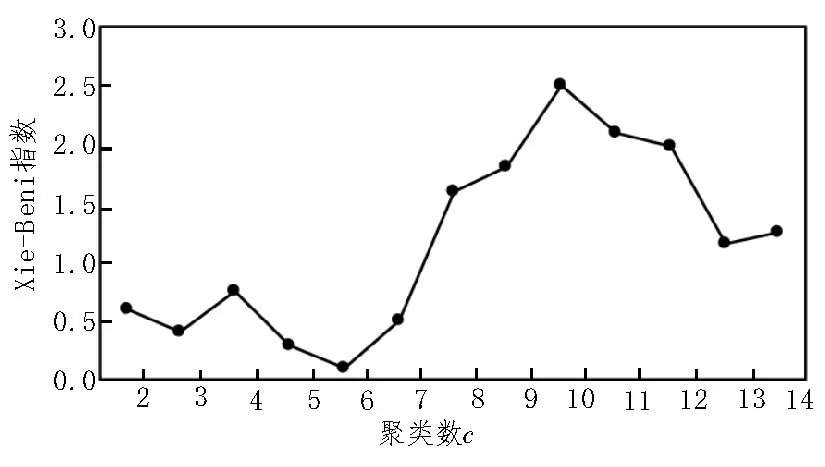
图4 Xie-Beni指数变化情况

3.2 造价评估的准确性分析

为验证该文所提基于FCM-LSSVM 算法的电网工程造价智能评估算法的性能，设置以下两种方案：

方案1：电网工程数据不经过聚类分析，直接作为LSSVM 算法的输入；

方案2：使用文中所提算法，电网工程数据经FCM 聚类后，将聚类结果作为LSSVM 算法的输入。

算法的计算时长如表2 所示，以10 个实际的电网工程数据测试该文所设计算法的准确性，计算结果如表3 所示。

表2 算法计算时长

表3 算法的准确性对比

由表2可知，在计算时长方面，方案1大于方案2。这是因为方案1 输入数据规模较大，增加了算法的计算时长；而方案2 虽然FCM 算法耗费一定的计算时间，但通过将具有相似特征的数据样本进行聚类分析，将聚类结果作为LSSVM 算法输入，大幅度提高了算法的计算速度。

由表3 可知，在准确性方面，对于10 个测试例来说，方案2 的误差均小于方案1。这是因为方案2 中经过FCM 的聚类分析，实现了数据样本的特征提取，减少了次要因素的影响干扰，使得LSSVM 算法能够充分挖掘电网工程造价与数据样本特征的关系，提高了电网工程造价评估的准确性。

4 结束语

文中基于电网工程投资造价评估分析系统，结合FCM 与LSSVM 算法，开展电网工程造价评估研究。通过算例分析表明，文中所提算法经过FCM 算法，实现特征相似的电网工程数据聚类，减少了LSSVM 算法处理数据的规模，大幅缩短了计算时长。同时FCM 算法实现了特征的提取，提高了电网工程造价评估的准确性。