分数阶混沌同步及其保密通信应用

2022-03-15李贤丽朱金元汤俊杰温玉玉秦显荣

电子设计工程 2022年5期

李贤丽，朱金元，汤俊杰，温玉玉，秦显荣

（东北石油大学物理与电子工程学院，黑龙江大庆 163318）

混沌信号具有对初始值敏感、不可预测、随机性强等复杂的非线性动力学性质，同时因为混沌的非线性动力学方程、初始条件、系统中的各个参数是确定的并且可以人为设定，所以混沌信号被广泛地应用在保密通信中[1]。混沌保密通信的前提是实现混沌同步，近些年学者们提出多种混沌同步方法如滑模同步[2]、投影同步[3]、状态观测器同步等[4]。但这些同步方法多数适用整数阶的混沌同步，该文通过设计合适的控制器来消除误差系统中的非线性项，可以简单快速地实现分数阶混沌同步，并在混沌同步的基础上使用混沌掩盖技术[5]进行保密通信研究。

该文基于分数阶EI-Nino 混沌系统，通过设计合适的控制器实现混沌同步。并在混沌同步的基础上设计了一种混沌掩盖保密通信方案。该设计的混沌同步速度快速且混沌电路仿真精度较高。并用Matlab 和Multisim 进行仿真，验证了该设计的有效性和可行性。

1 EI-Nino混沌系统

EI-Nino 混沌系统[6]方程为：

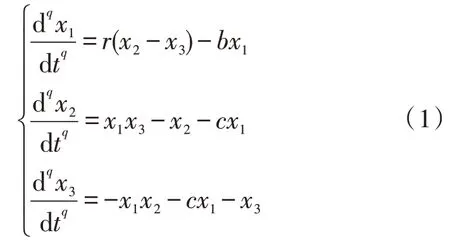
其中，0 ＜q＜1，x=(x1,x2,x3) 是系统的状态变量。取参数r=83.6，c=12 和初始值为(-2,3,5)，当q=0.95 时，系统随参数b变化的分岔图如图1 所示。

图1 EI-Nino系统随参数b 变化的分岔图

由图1 可知，在b∈(5,28) 范围内，EI-Nino 系统处于混沌状态。当取参数b=10 时，系统的相图如图2 所示。

图2 b=10 时，EI-Nino系统相图

由图2 可知，b=10 时，EI-Nino 系统处于混沌状态，与图1 的分析结果相符。因为混沌同步和混沌保密通信研究均需要利用到EI-Nino 系统的混沌状态，所以在下文的研究中，EI-Nino 混沌系统的参数均选取r=83.6，b=10，c=12，q=0.95。

2 控制器的设计

2.1 反馈线性化同步原理

设分数阶混沌系统如下：

其中，0 ＜α＜1，x=(x1,x2,…,xn)T∈Rn是状态向量，A∈Rn×n为混沌系统线性部分的常数矩阵，f(x)是混沌系统的非线性项。用式（2）系统做驱动系统，响应系统为：

其中，0 ＜α＜1，y=(y1,y2,…,yn)T∈Rn是状态向量，A∈Rn×n为混沌系统线性部分的常数矩阵，f(y)是混沌系统的非线性项，u=(u1,u2,…,un)T是需要设计的控制器。

令式（3）系统与式（2）系统的状态误差为e=y-x，误差向量e=(e1,e2,…,en)T，通过设计合适的控制器u使

引理1 分数阶线性系统如下：

其中，0 ＜α＜1，x=(x1,x2,…,xn)T∈Rn，C∈Rn×n为常数矩阵，如果C的特征值λi满足条件|arg(λi) |＞πα/2，则式（4）系统的零点是渐进稳定的，即

定理1 设计控制器为：

K∈Rn×n为常数矩阵，如果K能使A-K的特征值λi满足条件|arg(λi)|＞πα/2，则式（3）系统与式（2）系统渐进同步[7]。

2.2 EI-Nino系统反馈线性化同步

将式（1）作为EI-Nino反馈线性化同步的驱动系统。

响应系统为：

根据定理1，设计控制器，如下：

通过设置参数b的取值，使C的特征根全为负值，由引理1 可知误差系统式（8）的零点是渐进稳定的。式（1）系统和式（6）系统实现了同步。

2.3 混沌同步数值模拟

在式（1）和（6）中，当参数r=83.6，b=10，c=12和初始值为(-2,3,5)，q=0.95 时，用Matlab 对EI-Nino混沌系统进行同步仿真，如图3 所示。由图3 可知，EI-Nino 的各状态变量可以在很短的时间内达到同步，且同步过程中误差曲线很平滑，没有出现多次往返震荡的情况，该平稳同步过程有利于下文混沌电路的仿真。

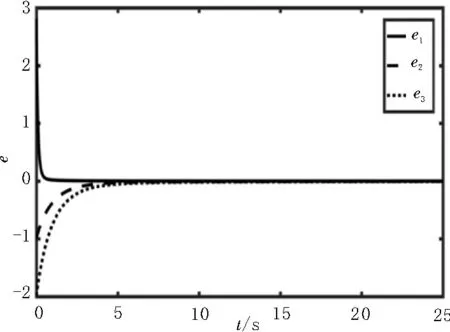
图3 EI-Nino同步误差曲线

3 保密通信电路设计

3.1 EI-Nino同步电路设计

传统的混沌电路模块化搭建[8-10]便捷，但对于分数阶混沌系统的仿真效果却不高，很难达到实验要求的精度。因此，该设计采用改进的模块化电路搭建方法[11-12]进行分数阶混沌系统的电路搭建[13-14]，所用电子元器件少且仿真精度高。

经过时间尺度变换、微分积分变换、积分方程作标准化处理等操作。根据式（1）搭建EI-Nino 驱动电路，如图4 所示。根据式（2）搭建EI-Nino 响应电路，如图5 所示。

图4 EI-Nino驱动电路

图5 EI-Nino响应电路

图4 中各电子元器件参数值如下：R1=100 kΩ，R2=31.897 93 kΩ，R3=31.897 93 kΩ，R6=1 000 kΩ，R7=31.25 kΩ，R8=12.5 kΩ，R11=1 000 kΩ，R12=31.25 kΩ，R13=12.5 kΩ，R4=10 kΩ，R5=10 kΩ，R9=10 kΩ，R10=10 kΩ。图 5 中，R14=100 kΩ，R15=31.897 93 kΩ，R16=31.897 93 kΩ，R17=1 000 kΩ，R18=31.25 kΩ，R19=12.5 kΩ，R20=1 000 kΩ，R21=31.25 kΩ，R22=12.5 kΩ。根据传递函数的计算方法设计出q=0.95 阶电路模块[15-18]，如图6 所示。图6 中，R23=75.835 1 MΩ，R24=3.563 7 MΩ，R25=0.036 7 MΩ，C1=0.257 8 μF，C2=0.191 6 μF，C3=0.686 8 μF。

图6 q=0.95阶电路模块

对图4 和图5 所组成的EI-Nino 同步电路的仿真结果如图7 和图8 所示。图7（a）、（b）分别与图2（a）、（b）进行对比可知该EI-Nino 电路设计的正确性，该电路可以对EI-Nino 混沌系统模型进行有效的模拟。图8 所示是EI-Nino 同步电路中的驱动变量与对应响应变量的时序图，在图8（a）、（b）、（c）中各驱动变量与对应响应变量成斜率为1 的正比例函数关系，说明响应系统电路与驱动系统电路达到了很好的同步状态。

图7 EI-Nino驱动电路吸引子相图

图8 EI-Nino同步电路时序图

3.2 加密与解密电路设计

加密与解密模块电路[19]如图9 所示，R26=10 kΩ，R27=10 kΩ，R28=10 kΩ，R29=10 kΩ，R30=10 kΩ，R31=10 kΩ，R32=10 kΩ，R33=10 kΩ，R34=10 kΩ。

图9 加密与解密模块电路

图4、图5、图6 和图9 组合成一个完整的混沌保密通信系统。混沌掩盖的原理是通过驱动-响应的方法使发送端和接收端的混沌信号保持同步，信息信号与混沌信号叠加后的信号具有类似噪声的形态，因为接收端和发送端的混沌信号事先已经保持同步，所以可以通过接收端信号减去已经同步的混沌信号得到恢复信号，这样就实现了保密通信的目的。文中原始信号为m，加密后的信号为s=m+x1，恢复信号为m′=s-y1，选取m=sin(t)进行保密通信仿真。图10 为原始信号，图11 为加密后的信号，可以看出原始信号得到了很好的掩盖加密。图12 为恢复信号，对比图12 和图10 可知原始信号得到了很好的恢复，说明该保密通信设计方案的可行性。