多径信号相关与信道相关阵列空间谱估计性能

李忠

（中国电子科技集团公司第二十二研究所，河南新乡 453003）

移动通信信号传输过程中，由于空间存在反射、散射、绕射等现象，存在大量的多径信号，形成多径信道信号传输。同一用户形成的多径信号通常被认为是相关的或相干的。在多径信道的信号传播环境下，由于信号相干或相关，一般子空间类算法[1-2]如MUSIC、ESPRIT 等信号子空间的秩降低，对多径相干信号DOA 的估计性能下降。为了解决多径相干信号的DOA 估计，相关的文献中提出了多种去相干处理方法，基本处理方法有两大类[3]，一类是降维处理，另一类是非降维处理。降维处理方法主要是空间平滑算法、修正MUSIC（MMUSIC）和矩阵重构算法等[4-9]，其中常用的空间平滑类处理算法可以分成前向空间平滑算法(FSS)、后向平滑算法(BSS)、前后向平滑算法(FBSS)；非降维处理方法主要有Toeplitz方法等[10]。信号通过多径信道传输不仅存在多径相干信号，同时接收阵列中不同接收信道存在信道的相关性。信道的相关特性由信道的空间特性和天线阵的配置共同决定。两个天线接收到的信号一般是相关的，其相关系数与天线距离和入射波的角度谱有关。目前关于信道的相关研究文献较多[11-12]，且主要以通信系统性能的影响研究为主[13-15]。在实际信号侦测系统中[16]，接收天线信道的相关性对信号测向性能具有一定影响，信道相关性对DOA 估计性能的影响未见相关文献研究。若不仅考虑到信号的相干性，同时考虑接收信道存在相关性，对DOA 估计性能又如何？文中从多径相关信号的DOA 估计性能出发，重点考虑信道相关性对DOA 估计的影响，引入相关系数矩阵，给出了阵列协方差矩阵形式，分析存在信道相关性情况下，对DOA 估计的影响；并综合分析存在信号相关与信道相关双重因素下，多径信道的DOA 估计性能，为信息系统DOA 性能评估提供指导。

1 信号的相关性

两个平稳信号si(t)和sl(t)之间的相关系数为：

将信号之间的相关性定义为：

根据以上定义，假设K个相干源，其形式为：

设αi为第i个信号相对于s0的衰落系数，阵列的输出矢量为：

式中，N(t)为噪声矩阵，A为阵列流型矩阵，A=[a(θ1),a(θ2),…,a(θK)]，其中，a(θ1),a(θ2),…,a(θK) 为导向矢量。

2 信道相关性

由于接收信道天线之间的相互影响以及多径入射波信号存在空间谱扩展，接收信道存在空间相关性，存在信道相关性条件下，阵列流型矩阵将A变为：

式中，r为信道相关系数矩阵，阵列接收矩阵如下：

将阵列中第m个阵元和第n个阵元接收信号的空间相关性定义为：

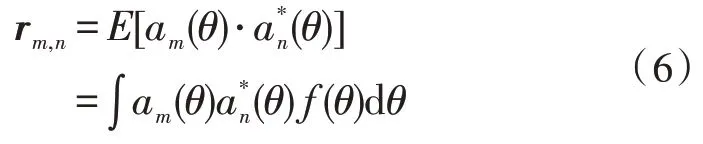
式中，am(θ)、an(θ)为阵列流型矩阵A的导向矢量元素，f(θ)为入射信号概率密度角分布函数。均匀直线阵情况下，阵元间距为d(d＜λ/2）。

1）假设入射角概率分布服从高斯分布，分布函数满足：

式中，θ∈[θ0-Δ,θ0+Δ]，Δ 为角度扩展，θ0为中心到达角，误差系数σ为分布的标准差。

2）假设入射角概率分布服从均匀分布，分布函数满足：

将分布函数代入相关系数积分表达式中，在角度扩展较小的情况下，cos Δ ≈0，sin Δ ≈0，根据式（6），计算结果如图1～3 所示。

图1 不同分布下空间相关性随阵元间距波长比的变化（σ=10°，θ0=45°）

通过图1 可以看出，不同的入射角概率分布模型中，阵元相关性随阵元间距增加而产生明显的差异性。以常见的高斯分布为例，图2 与图3 表明，在相同阵元距离和入射中心角θ0的条件下，标准差σ越小，空间相关性越高；相同阵元距离和标准差σ的条件下，入射中心角θ0越大，空间相关性越高。

图2 相同入射中心角下空间相关性随阵元间距波长比的变化（θ0=45°）

图3 不同入射中心角下空间相关性随阵元间距波长比的变化（σ=10°）

作为实例，图4 给出了2×2 MIMO 系统的信道容量随SNR变化的曲线，针对不同的发射端相关系数α和接收端相关系数α，对比完全独立的MIMO 信道(α=β=0)与完全相关的信道(α=β=1.0)，独立不相关信道的信道容量MIMO 容量大幅提高。

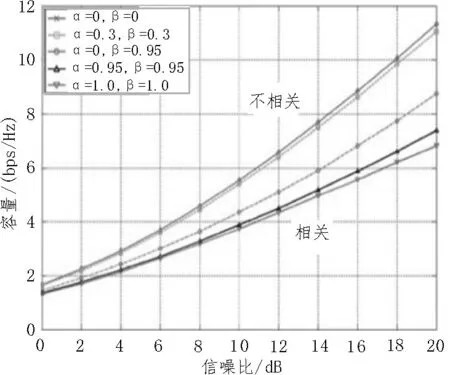
图4 不同发射和接收相关系数情况下，2×2 MIMO系统的平均信道容量随信噪比的变化曲线

3 双重因素综合存在情况下的DOA估计

3.1 相关/相干信号DOA估计

考虑到信号的相关性或相干性，阵列协方差矩阵由式（9）可得：

式中，为相对信号功率，ρ⋅ρH可以看作信号相干系数矩阵。

通过该阵列协方差矩阵构造MUSIC 谱函数进行DOA 估计。

设阵元数N=8；阵元间距d=λ/2；入射信号数K=3，入射角θ=[5°,10°,15°]。快拍数为1 000，信噪比SNR=20 dB。

情况一：信源s1与信源s2相关，信源s3独立；信源s1衰落因子为1；信源s2衰落因子为0.8，相移π/6。

情况二：信源s1、s2、s3相互独立。

以上两种情况下计算的空间谱结果如图5所示。

图5 信号独立与信号相关空间谱分布

从图5 中可以看出，相互独立的信号均能独立分辨估计，若假设接收信号s1、s2存在相关性，除了独立信源s3(θ=15°)明显可分辨外，两相关信源s1、s2空间谱无法分辨，阵列谱估计性能降低。

3.2 信道相关性DOA估计

若考虑到信道的相关系数矩阵后，阵列协方差矩阵由式（5）可得：

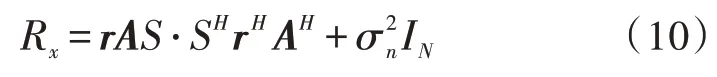
其中，r为文中引入的相关系数矩阵：

相关系数矩阵元的求解见式（6）。

通过该阵列协方差矩阵构造MUSIC 谱函数，并进行DOA 估计。

设阵元数N=8；阵元间距d=λ/2；入射信号数K=3，独立信道下入射角θ=[5°,10°,15°]，快拍数为1 000，信噪比SNR=20 dB，相关信道入射信号角分布服从高斯分布，入射中心角θ0=10°，计算信道相关性对MUSIC 谱的影响结果,信道独立与信道相关空间谱分布如图6 所示。

图6 信道独立与信道相关空间谱分布

从图6 中可以看出，在相同阵元距离和入射中心角θ0=10°的条件下，随着标准差σ越小，空间相关性越高，由于信道相关性增加，阵列的空间谱分辨率显著恶化；同样，通过分析得知，在相同阵元距离和标准差σ的条件下，入射中心角θ0越大，空间相关性越高。

3.3 双重因素下的DOA估计

由相干信号协方差矩阵式（9）和考虑信道相关性的阵列协方差矩阵式（10）可知，双重影响因素的情况下，阵列的协方差矩阵为：

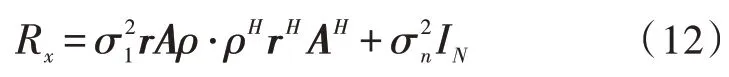
式中，为相对信号功率，r为相关系数矩阵，ρ⋅ρH可以看作信号相干系数矩阵，A为阵列流型矩阵。

通过该阵列协方差矩阵构造MUSIC 谱函数进行DOA 估计。假设计算条件如3.1 节与3.2 节信号相关与相关信道的情形，两个因素综合考虑后计算结果与3.1 节和3.2 节计算结果进行对比分析,信号相关与信道相关空间谱分布如图7 所示。

图7 信号相关与信道相关空间谱分布

从图7 中可以看出，综合考虑到信源的相关性与信道的相关性，两个相关信源s1、s2无法分辨，第三个独立信源s3(θ=15°) 谱峰也发生了明显的偏移。计算结果表明，随着标准差σ的减小，信道的空间相关性增大，空间谱甚至无法识别。由此可以看出，双重因素影响下，阵列空间谱估计性能失效。

4 结论

文中通过分析计算表明，多经相关信号经过相关多径信道接收，其DOA 估计不仅因缺秩造成信号无法分辨，甚至出现任何接收信号的DOA 都无法估计，导致谱估计分辨率与准确度显著降低，甚至失效，由此产生的影响结果需要在工程设计中引起高度重视。系统设计中，可通过去相关技术消除信号的相干性，同时通过调整接收信道空间布局降低相关系数，降低信道相关性对测向系统的影响，避免双重因素导致系统完全失效。