一维多尺度卷积神经网络及其在滚动轴承故障诊断中的应用

张成帆,江泽鹏,曹伟,陈伟,张敏

(1. 西南交通大学 机械工程学院,成都 610031； 2. 轨道交通运维技术与装备四川省重点实验室,成都 6100313. 西南交通大学 盾构/TBM装备摩擦学设计实验室,成都 610031)

滚动轴承是在机械设备中具有广泛应用的关键部件之一,由于过载,疲劳,磨损,腐蚀等原因,滚动轴承在机器运行过程中容易损坏,在实际生产中超过50%的旋转机器故障与轴承故障有关[1]。为保障实际生产中旋转机械不出现安全事故,使用有效的诊断算法对滚动轴承进行诊断具有十分重要的意义。但由于实际生产中来自滚动轴承监测系统的数据量日益增多,各状态参数之间存在强耦合、非等效等复杂的对应关系,很难实现数据特征的高效提取。自Hinton等[2]首次探讨了使用深度学习进行大数据处理以来,近年来受到学术界和工业界的广泛重视,越来越多的学者开始了利用深度学习进行滚动轴承故障诊断的研究。

目前利用深度学习进行故障诊断的方法,大多集中于使用预提取的特征作为神经网络的输入的方法。如Unal等[3]利用希尔伯特-黄变换和傅里叶变换提取故障特征后使用神经网络进行轴承故障诊断。陈文戈等[4]使用小波变换提取信号在不同频道上的特征作为神经网络的输入进行轴承故障分类。黄竞楠等[5]通过奇异值分解和经验模式分解的方式提取含有主要故障信息的分量,然后从选取的本征模函数分量中提取故障特征参数作为神经网络输入进行轴承故障诊断。Zhang等[6]利用自回归模型提取轴承振动信号特征,并通过优化后的人工神经网络实现故障识别。Wang等[7]直接将轴承采样信号的希尔伯特包络谱作为特征向量,之后使用深度置信网络对特征向量进行分类完成轴承故障分类。Khajavi等[8]使用离散小波变换进行信号预处理,利用神经网络对输入的归一化的离散小波系数进行轴承故障分类。上述方法都受到需要预提取特征的制约,所提取的特征仅针对特定场景有效,并且只将神经网络作为一个分类器使用,而忽视了神经网络强大的非线性拟合能力本身就具有自动提取特征并进行分类的能力。

因此有部分学者提出端到端的深度学习方法来进行轴承故障诊断,即无需对信号做特征提取的工作,直接利用深度学习自身的非线性拟合能力自动完成特征提取和故障分类的工作。其中,Tamilselvan等[9]提出一种基于深度置信网络的故障诊断方法,庄雨旋等[10]提出通过基于LSTM的轴承故障端到端的诊断方法,雷亚国等[11]提出基于无监督学习和有监督学习相结合的深度置信神经网络的轴承故障诊断算法,这些方法验证了端对端的深度学习方法在轴承故障识别方面的可行性和无需预先提取特征的优势。实际上,滚动轴承的振动信号属于一维数据,也有不少学者使用适合处理一维数据处理的一维卷积神经网络来实现端到端的滚动轴承故障诊断工作。曲建岭等[12]提出基于一维卷积神经网络的层级化智能故障诊断模型,可同时识别滚动轴承的故障类型和故障程度。Zhang等[13]提出利用一维卷积神经网络的一种端对端的滚动轴承故障诊断算法。Wang等[14]对使用粒子群优化算法对一维卷积网络的超参数进行优化,以适应滚动轴承故障诊断。吴春志等[15]使用一维卷积网络进行齿轮箱的故障诊断方法并取得了高于传统方法的诊断效果。上述方法都是使用单一尺度卷积核的一维卷积神经网络,造成了信息易在池化层产生丢失现象[16]。

综上所述,为了解决使用深度学习需要使用预提取的特征作为输入,以及使用单一尺度卷积核的一维卷积神经网络易在池化层丢失部分信息的问题。提出一种一维多尺度卷积层对信号进行特征提取,然后由全连接层实现分类识别的一维多尺度卷积神经网络的滚动轴承故障诊断方法。

1 一维卷积神经网络

卷积神经网络是属于深度学习中的一种模型,因其能够从数据中学习并提取深度特征信息并且在图像识别领域具有强大的泛化能力而有名。而一维卷积神经网络则是使用一维卷积核来实现卷积操作的卷积神经网络。一维卷积神经网络的卷积运算部分[17]一般由一维卷积层和池化层构成,而后连接一个全连接层来实现最后分类结果的输出,为避免模型产生过拟合现象,还可在全连接层间添加Dropout层。

1.1 一维卷积层

一维卷积神经网络中的核心是一维卷积运算。在某个卷积层上通过多个卷积核对上层输出的激活值进行卷积后加上偏置,然后经过一个激活函数即可得到下一层的激活值,这个过程的表达式为

(1)

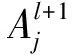
假设输入大小为n×1,卷积核大小为m×1,卷积核个数为a,移动步长为s,则输入大小为c×a,其中c=(n-m)/s+1。不使用激活函数的卷积运算过程见图1。

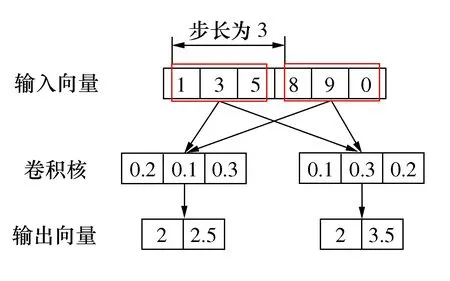
图1 不使用激活函数的卷积运算

1.2 池化层

池化层负责将上层卷积层输出的激活值进行降维,不仅可以减少神经网络计算的数据量,还能一定程度上维持激活值的特征尺度不变性。池化方法主要有最大值池化和平均池化,最大值池化即选择池化窗口中的最大值为输出,平均值池化即输入池化窗口中值的平均值。设输出池化层的m×1 维矩阵X=[x1,x2,…,xm]T, 池化窗口大小为s,则池化之后输出的数据为n×1维矩阵Y=[y1,y2,…,ym]T,输入长度m和输出长度n的关系为

(2)

式中“⎣ 」”表示向下取整,即池化操作可以使输入矩阵尺寸变小。池化方法主要分为平均池化和最大池化两种。平均池化输出池化窗口内的平均值,最大池化输出池化窗口内的最大值。池化运算过程见图2。

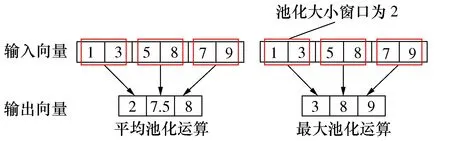
图2 池化运算

1.3 Dropout层

Dropout层中随机将上层某个神经元的输出置为零,也就是关闭了部分神经元,这种方法可以强迫神经网络只能使用部分神经元进行训练,从而避免神经网络对部分神经元过于依赖的问题,可以降低模型出现过拟合的概率。Dropout过程表达式为

Al+1=(Al×D)/keep-prob

(3)

式中：Al+1为Dropout层输出；Al为进行Dropout操作的输入；D为和Al大小相同,内部元素初始为全为1的矩阵，内部元素按照keep-prob大小进行随机置零,若keep-prob为0.8,则表示全1矩阵D中有20%的元素被随机置零。为了保证输入矩阵Al的期望值不变,置零后的A矩阵中的每个元素还需要除以keep-prob。

1.4 全连接层

输入数据经过多个卷积层和池化层交替传播后,还需要依靠全连接层提取的特征进行分类,该层将上层输出的矩阵降为1×n维矩阵,经过Softmax激活函数输出该样本被分为n类中某一类的概率。

2 模型设计

2.1 一维多尺度卷积层

滚动轴承振动信号往往随着损伤点的出现而产生非周期冲击信号,并且滚动轴承共振频率随着转速而发生改变[18],这就导致使用单一卷积核进行特征提取的卷积网络可能会产生部分特征丢失的现象。同时,不同转速和负载工况下的滚动轴承故障信号特征不同,单一尺度的卷积核难以应对变工况下的滚动轴承故障诊断,若需将算法应用到其他工况下的故障诊断时,只能重新进行参数调试过程。为此,本文中提出一种一维多尺度卷积层(One-dimensional multiscale convolution layer,1D-MCL)来取代常规卷积网络中的单一尺度卷积层,其结构如图3所示。

图3 一维多尺度卷积层

该模块由四支分支构成,每只分支所使用的卷积核尺度都和其他卷积核尺度不同,这样就能从上一层输出中提取到多尺度的特征,然后将每支分支卷积得到的特征向量进行拼接作为下一层的输入。一维多尺度卷积层中各分支卷积核个数如表1所示。

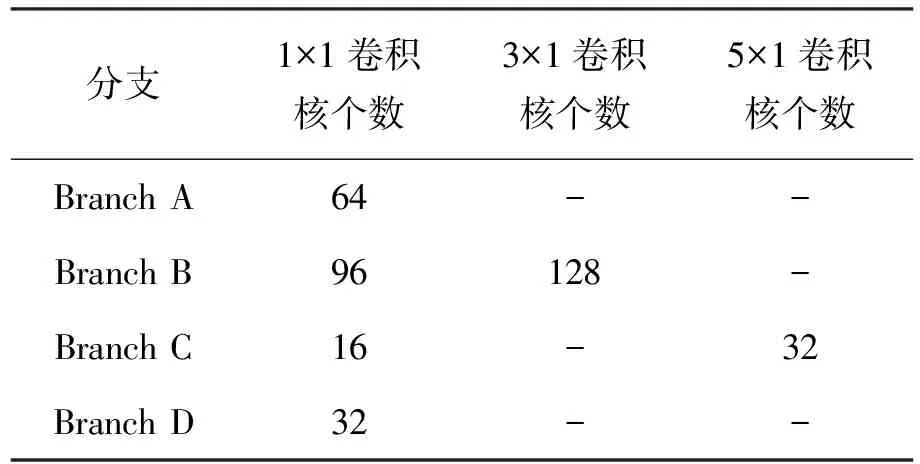
表1 各分支中卷积核个数

一维多尺度卷积层运算过程为

(4)

2.2 模型结构

本文试验搭建的一维多尺度卷积神经网络(One-dimensional multiscale convolutional neural network,1D-MCNN)模型由1个输入层,2个卷积层,2个池化层,3个一维多尺度卷积层,1个Dropout层和一个全连接层构成,其结构见图4。

图4 试验采用的1d-MCNN模型结构

试验所采用的每个滚动轴承信号样本长度都为6 000的一维向量,通过前两层一维卷积层和一个最大池化层迅速缩短向量长度同时增加通道数,然后进入3个堆叠的一维多尺度卷积层进一步提取特征,最后使用一个全局平均池化层,使数据通道数变为1便于后面全连接层进行分类。全局平均池化层和全连接层之间添加一个Dropout层,避免模型产生过拟合现象。轴承样本数据进入神经网络中的尺寸变化见表2。

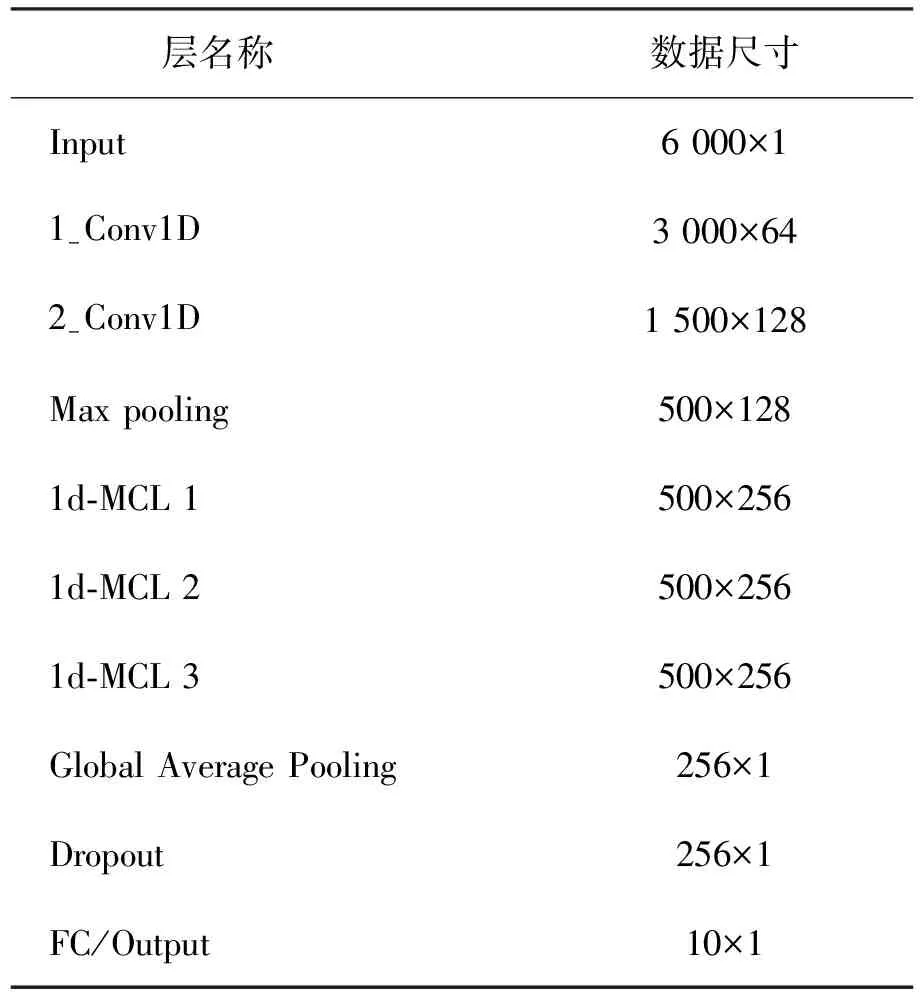
表2 神经网络中数据尺寸变化

3 试验分析

3.1 数据来源

试验数据来自于美国凯斯西储大学轴承数据中心公开的滚动轴承故障振动数据集[19]。包括电机在不同负载下使用加速度传感器,测得的驱动端、风扇端滚动轴承的振动信号。

每种载荷下都含有滚动轴承的4种状态:正常、滚珠故障、内圈故障、外圈故障,且每种故障类型都包含3种不同的故障程度,分别为0.177 8 mm损伤直径、0.355 6 mm损伤直径和0.533 4 mm损伤直径。每种载荷下根据故障类型和损伤直径的不同，一共有10种状态，数据集分布情况如表3所示。

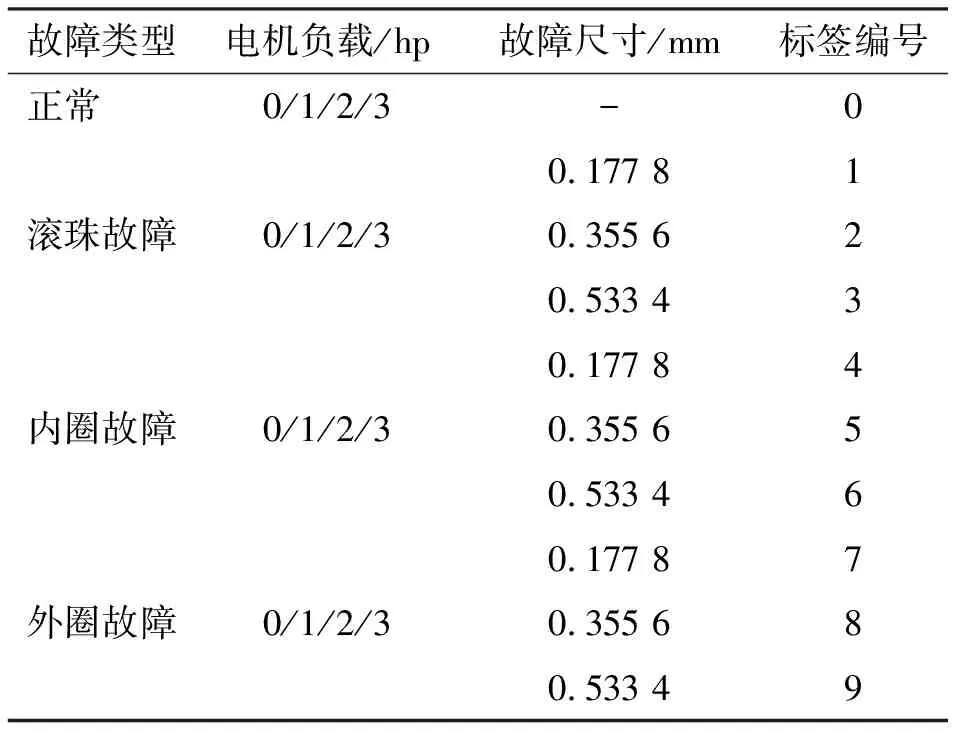
表3 试验数据集组成

3.2 数据扩增

为了进一步提高模型的泛化能力,需要大量的数据来对神经网络进行训练。然而受限于种种原因,往往现实中无法收集到大量的数据。为此本文使用了滑动窗口数据采样来完成数据的扩增,以适应神经网络对大量数据的需求。滑动窗口数据采样如图5所示。

图5 滑动窗口数据采样

假如采样窗口长度为f,采样窗口移动步长为s,数据总长度为L,则数据数量n计算式为。

n=⎣(L-f)/s」

(5)

原数据集中每种载荷下各种故障数据长度为120 000,设置滑动采样窗口长度6 000,步长1 000,则可得每种故障状态下的数据114组,10种故障状态共计1 140组数据。相比单纯设置6 000长度分割一组数据的方法,该方法将数据数量扩增了5.7倍。

3.3 试验结果与分析

3.3.1 不同工况下的诊断结果

将1d-MCNN学习率设置为0.000 1,Dropout比率设置为0.3,使用交叉熵损失函数,并利用Adam梯度下降算法进行权重更新。训练数据分为70%和30%两部分,70%部分数据用于训练网络,更新模型权重参数,剩余30%部分数据用于评估模型性能。模型对不同载荷下的诊断结果如图6所示。

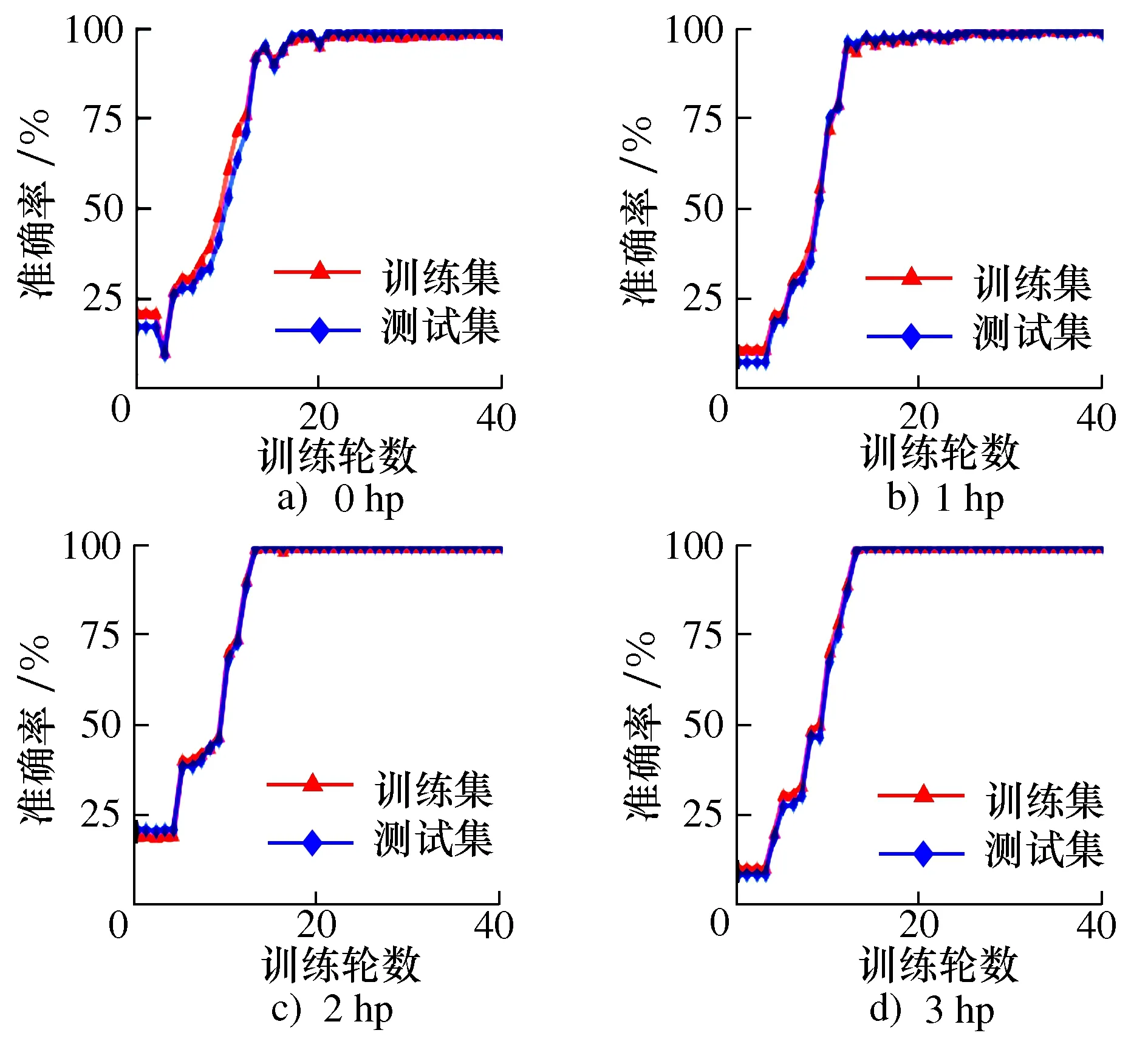
图6 4种载荷样本训练过程中的Accuracy曲线

由图6可以看出在4种载荷下的训练出的神经网络均能在训练集和验证集上达到接近100%的识别准确率。

为了展示1D-MCNN算法对滚动轴承故障的诊断效果,绘制了预测载荷为2 hp数据集的轴承误分类矩阵图。

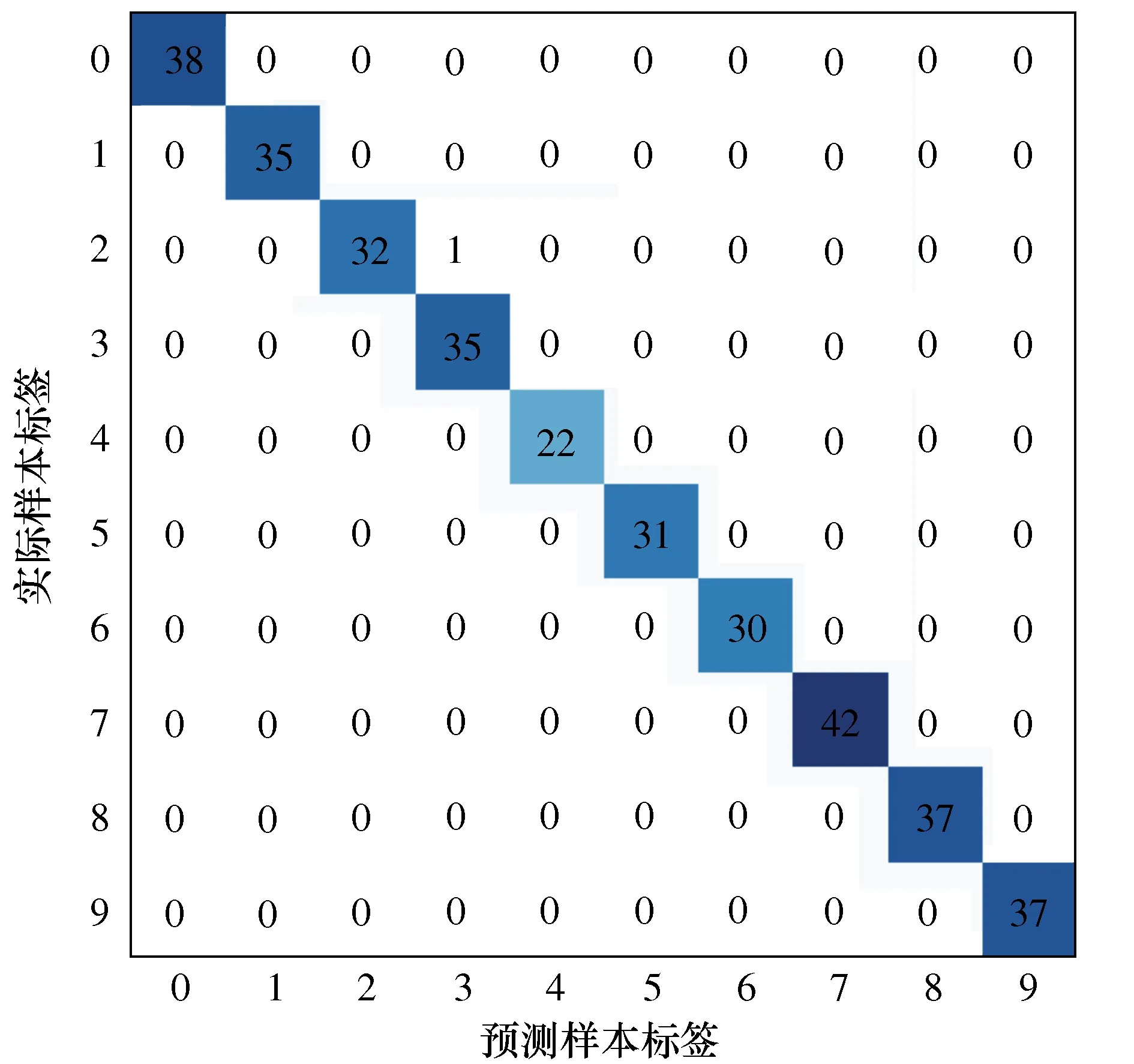
图7 滚动轴承故障误分类矩阵

图7中坐标值从0到9分别为表3中的标签编号,代表滚动轴承的不同状态。阴影中的数字表示为实际样本标签和预测样本标签相符合的个数。从图7中可以看出,测试的340个样本中,除了类别2中有一个样本被误分类至类别3中,其他预测样本的分类结果均正确。可以说1D-MCNN算法在测试中取得令人十分满意的分类结果。

3.3.2 模型提取特征能力分析

模型若能在小样本量下依然能取得较好的诊断结果,说明模型具有从故障信号中准确提取故障特征的能力。为了验证模型提取特征的能力,使用了训练集和测试集划分比例分别为9∶1、8∶2、7∶3、6∶4和5∶5的数据集进行测验,其结果如表4所示。

表4 不同训练集与测试集比例对诊断结果的影响

从表4中可以看出,当训练集占比为50%时诊断准确率最低,为99.43%,而训练集占比为90%时诊断准确率最高,为99.98%。这说明了训练样本的数量越多,样本内部蕴含的故障特征越具有针对性,训练出来的模型诊断性能越好。为展示1D-MCL提取特征的能力,采用t-SNE技术[20]将模型中三层1D-MCL输入的高维特征映射成二维特征进行可视化,可以看出各种故障类型的诊断样本从图8a)中可以看出第一层1D-MCL输出时还处于无序的分布状态,而从图8b)、图8c)中可以看出经过第2个、第三层1D-MCL模块处理之后,同一种故障类型的样本都很好的聚集在一起,而不同的故障类型的样本则被有效的分离开,这说明1D-MCL层具有良好的故障模式捕捉能力。

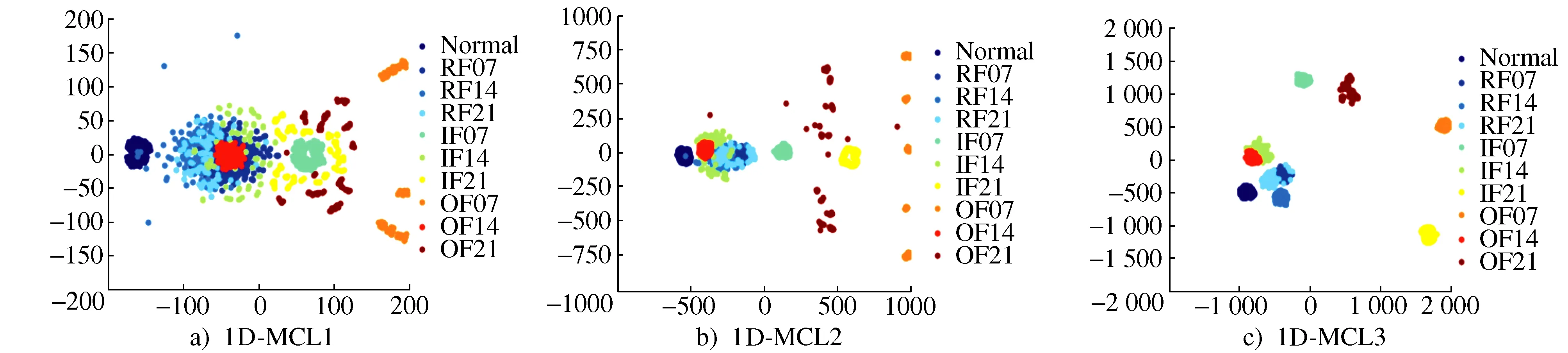
图8 神经网络中间层输出降维可视化

3.3.3 与其他算法对比分析

最后使用了支持向量机(Support vector machine,SVM)、BP神经网络和循环神经网络(Recursive neural network,RNN)作为对比。所有模型输入的均是长度6 000的滚动轴承振动信号,SVM采用高斯核函数,惩罚参数30,gamma取0.001;BP网络设置神经元数量为3 000和1 000的两层中间层,使用Softmax分类器;RNN网络使用神经元数量分别为500、200、50的三层门循环单元(Gated recurrent unit,GRU)中间层,其各个模型的诊断效果如表5所示。从表5可以看出,除1D-MCNN以外,其他方法在不同载荷下的诊断效果有着较大的偏差,不能适应不同工况下的诊断工作,如使用同一参数进行训练的RNN用来进行诊断时,0载荷下的诊断正确率为85.29%,而3 hp下的诊断正确率却高达99.41%,若要使RNN在其他载荷下也取得较好的诊断效果则需要反复多次的进行参数调整。而无论在何种载荷下,无需进行参数调整的1D-MCNN的诊断精度都在99%以上,说明了1d-MCNN具有能够在不同工况下进行诊断的适应性。

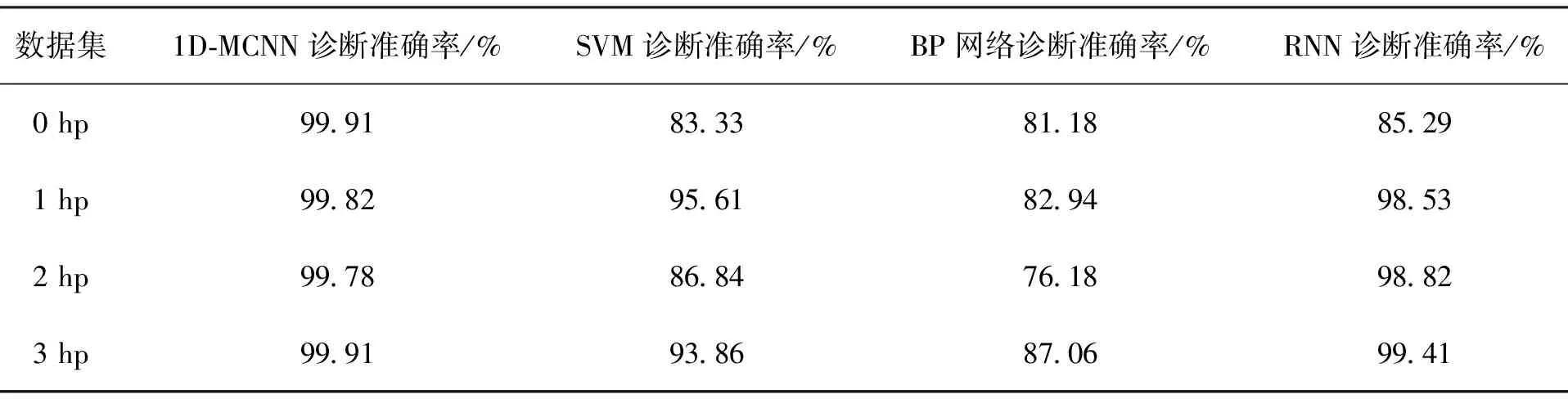
表5 不同模型的滚动轴承故障诊断结果

4 结论

针对轴承振动信号一维性的特点,传统一维卷积网络使用单一尺度卷积核提取特征可能会造成特征丢失的问题,提出了一种一维多尺度卷积层,设计了使用一维多尺度卷积层进行特征提取的一维多尺度卷积神经网络。实现了轴承故障特征的自动提取,摆脱了传统深度学习方法依靠预提取特征输入的依赖。试验表明,本文所使用方法对于不同载荷下的滚动轴承均能准确诊断出其故障位置和故障程度,且准确率优于常见诊断方法。通过可视化分析

一维多尺度卷积层的输出可以看出本文提出的一维多尺度卷积层具有良好的特征提取能力,因此其故障诊断正确率更高。以上试验和结果表明,本文方法对滚动轴承故障诊断具有一定的实用价值,是大数据环境下滚动轴承故障诊断的一个可行的方案。