共轴式双旋翼推力吸附机器人平台设计
2022-03-15薛朝军王海波
薛朝军,王海波*,
(1. 西南交通大学 机械工程学院,成都 610031;2. 轨道交通运维技术与装备四川省重点实验室,成都 610031)
随着我国经济的不断发展,基建项目的不断增多,基建设施老化的现象日益普遍,对老化的基建设施进行安全防控成为普遍的共识。桥梁安全事故频发,据不完全统计,2005~2018年全国至少垮塌了28座大中型桥梁。快速、高效、便捷的检测平台是能加快基建设施进行安全防控工作,同时也是顺利完成安全防控工作的保障。现有的爬壁机器人吸附平台主要有:真空吸附、负压吸附、磁吸附、仿生吸附和推力吸附。真空吸附主要依靠吸盘作为吸附腔体,理想情况下的吸盘与壁面之间应完全贴合不存在漏气,真空吸附机器人平台一般以多吸盘组交替吸附的形式实现在壁面上移动,但是对壁面的平整度要求高;负压吸附一般采用单吸附腔结构,通过特殊的弹性裙边和气囊进行密封,保证了负压的形成,进而保证了附着力,但只能在一个壁面上行走,不能实现从壁面到另一个壁面的跨越;磁吸附是依靠电磁体或者永磁体的磁力吸附于壁面,只适用于具有导磁性的壁面,不具普遍性;仿生吸附模仿生物的吸附机理或者肢体结构,对生物学、材料学、化工技术、微制造技术等学科的要求较高,很难应用于实际并且其负载能力往往不高;推力吸附利用轴线与壁面成一定角度的螺旋桨或风扇产生的高速气流来实现吸附的。推力吸附机器人平台有如下优点:1) 灵活的移动;2) 搭载一定的负载;3) 对壁面平整度无要求;4) 实现简单壁面跨越。而这些能力满足桥梁检测对平台的要求。[1-5]
1990 年日本的Nishi与Miyagi[6]推出了推力型爬壁机器人平台,它利用直升机原理,由螺旋桨产生的高速气流带动机器人高速移动,用柴油机提供动力,整体结构较大,不适用于小型检测平台。 2016年和2018年E-JUST的Alkalla等[7-8]分别提出了EJBot-Ⅰ和EJBot-Ⅱ爬壁机器人平台,都由同轴的、两个反向旋转的螺旋桨提供推力;Ⅰ型是外接电源,轮式行走,能在竖直壁面和天花板上进行攀爬;Ⅱ型是自带电源,履带式行走,能实现在壁面短暂的停留,通过舵机控制支撑臂与机器人平台地盘的角度实现地面和垂直壁面的过渡;但是两者都没有对螺旋桨进行选型分析,没有对旋翼直径与整机重量的关系进行空气动力学分析,把旋翼和机器人平台孤立开来。2017年泰国的Sukvichai 等[9]提出的纵列式双螺旋翼爬壁机器人平台,能实现地面与竖直壁面的过渡,但是机器人几乎没有负载能力。VertiGo是一款由苏黎世迪斯尼研究中心和ETH合作开发,2016年公开发表,能够从地面过渡到墙壁的爬壁机器人平台,能够在壁面上灵活移动,但是负载能力差[10]。国内,中南大学的徐聪和张羽等[11-12]分别在2013年和2019年提出了利用涵道风扇的爬壁机器人平台和球形螺旋桨的爬壁机器人平台,能实现转向、悬停及任意角度平面内行驶,但是存在壁面停留时间短和几乎不具备负载能力等问题。
本文在EJBot-Ⅱ的基础上设计了推力吸附机器人平台,并通过Fluent进行2维的外流场计算,以确定旋翼的安装角;再确定旋翼直径、旋翼需用功率与整机重量三者的关系,建立Simulink模型对旋翼直径进行参数化设计。使平台更加轻量化和便捷化,为机器人平台下一步的设计作铺垫。
1 机器人平台设计
平台主要有4部分构成:旋翼机构、机架、履带行走机构和翻越机构,如图1所示。
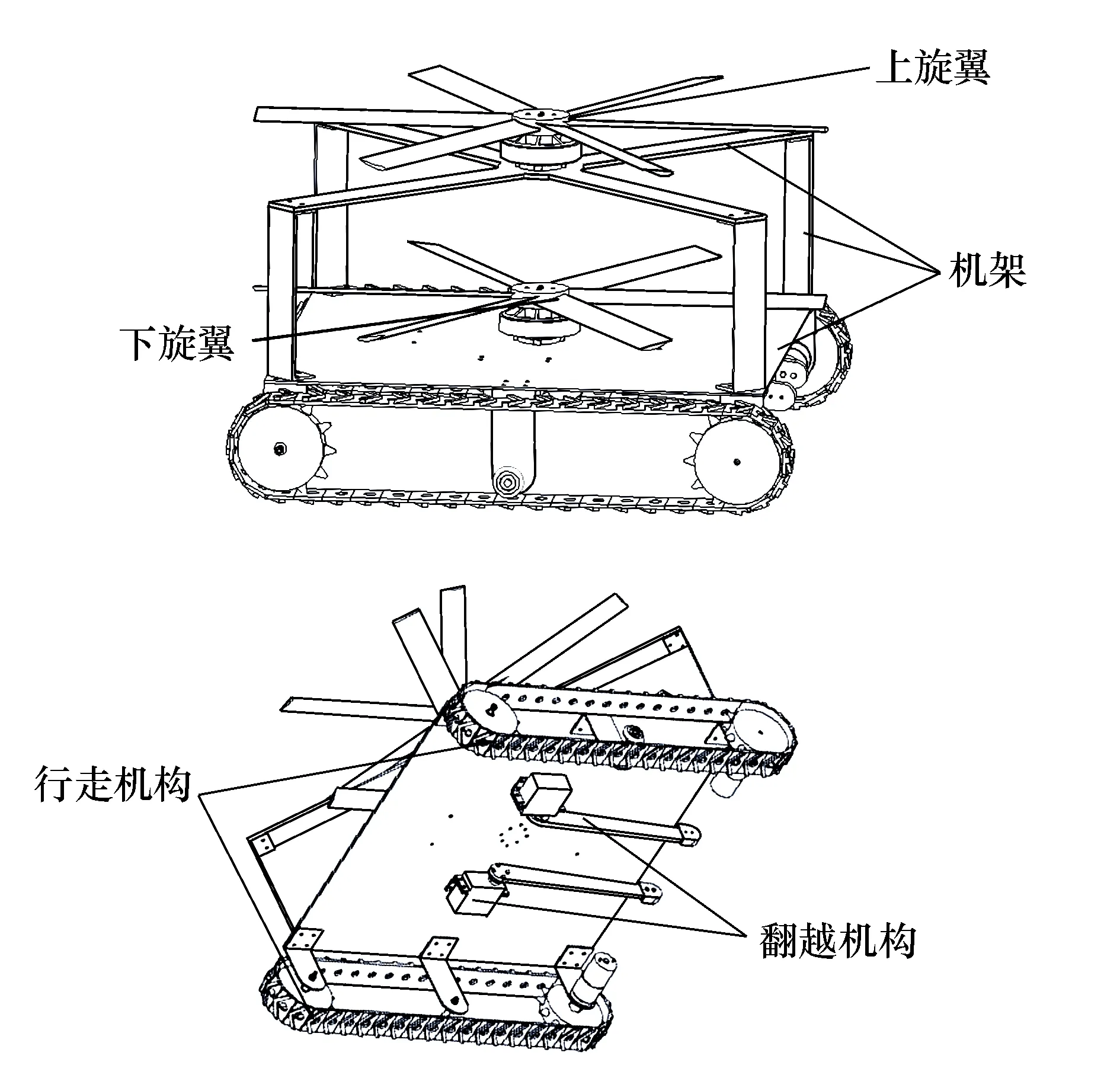
图1 机器人平台
机器人平台使用共轴式双旋翼转动提供正压力,上、下两旋翼通过正反转来抵消旋翼转动产生的扭矩;机器人平台通过履带与壁面的接触并挤压产生摩擦力而停留在壁面上;通过无线传感技术对旋翼系统、行走系统和翻越系统进行控制,使机器人平台到达预设的位置。
旋翼系统为机器人平台提供正压力,是保证平台停留在壁面上的关键。影响旋翼的推力主要因素有:旋翼的迎角、直径与转速。在一定范围内,迎角、直径与转速分别和旋翼产生推力的大小成正相关。
机架是机器人平台的主体,主要功能有:固定功能部件和传递旋翼产生的推力。整体重量随着旋翼直径的变化而变化。
机器人平台的行走方式采用履带式,具备与壁面接触面积大、对壁面平整度要求低和牵引力大等优点。履带使用橡胶材质,与混凝土面的摩擦系数为0.4。有如下优点:1) 灵活的移动;2) 对壁面平整度无要求;3) 稳定性较好。主要部件为:履带和驱动电机。
通过无线传感技术对翻越机构进行控制,调整翻越机构与机器人平台底盘的夹角,从而控制机器人平台的姿态,使机器人平台能够实现从一种壁面到另一种壁面的简单跨越。
2 数值方法与模型
在确保能够顺利作业前提下,机械结构设计结合空气动力学使机器人平台的能耗最小、成本最低和自身重量最轻。而影响旋翼的推力主要因素有:旋翼的迎角、直径与转速。先对选定翼型进行2维的外流场计算,求得“最经济状态点”,确定迎角。在确定迎角后,拉力一定,转速和直径共同决定旋翼电机的功率,影响电池的重量;而直径又与机架、履带行走机构、支撑翻越机构和旋翼机构的重量成正相关。由此,建立Simulink仿真模型,最后旋翼在某直径处,求得最轻重量的机器人平台。
2.1 安装角的确定
本文采用NACA4412翼型,无扭转角。对翼型进行外流场计算,以翼型弦长C=0.03为参考长度,计算域左、右边界距离翼型尾缘分别为10C、14C,上、下边界距翼型弦线都为10C,采用渐变网格,靠近翼型的网格加密,远离翼型后的网格间距逐渐增大,如图2所示。求得在Re=8×104、 1.6×105、 2.7×105下,升力系数CL、阻力系数CD随迎角α从-6°增大到20°的变化,分别如图3a)、图3b)所示[13-14]。
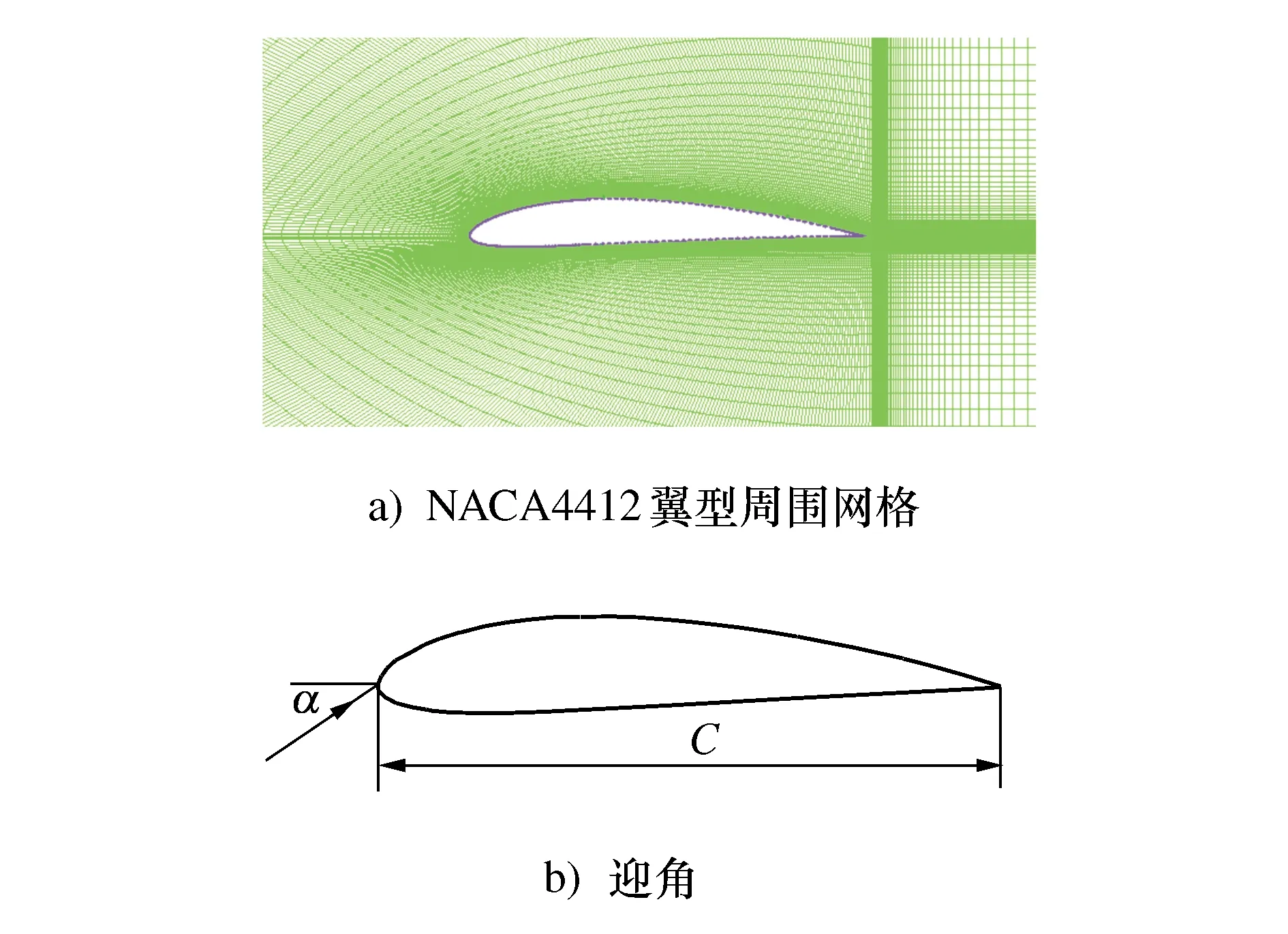
图2 计算模型
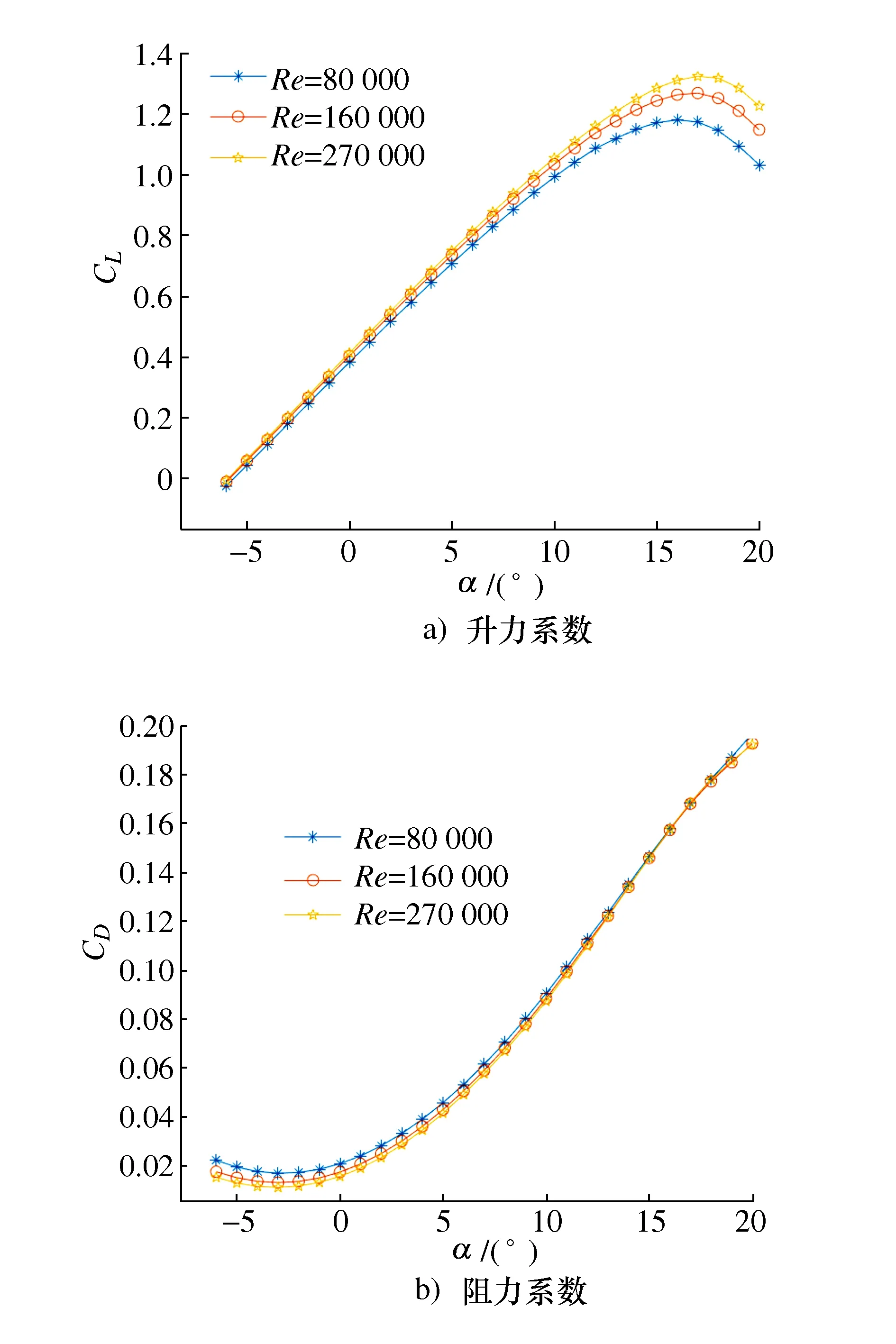
图3 升、阻力特性曲线
如图3所示,在-6°至10°的时候,升力系数与迎角呈线性相关。在Re=8×104、 1.6×105、 2.7×105下,对应CL1、CL2、CL3与迎角α的关系:
CL1=0.064 37×α+0.376 2
(1)
CL2=0.066 02×α+0.397 9
(2)
CL3=0.066 9×α+0.408
(3)
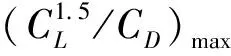
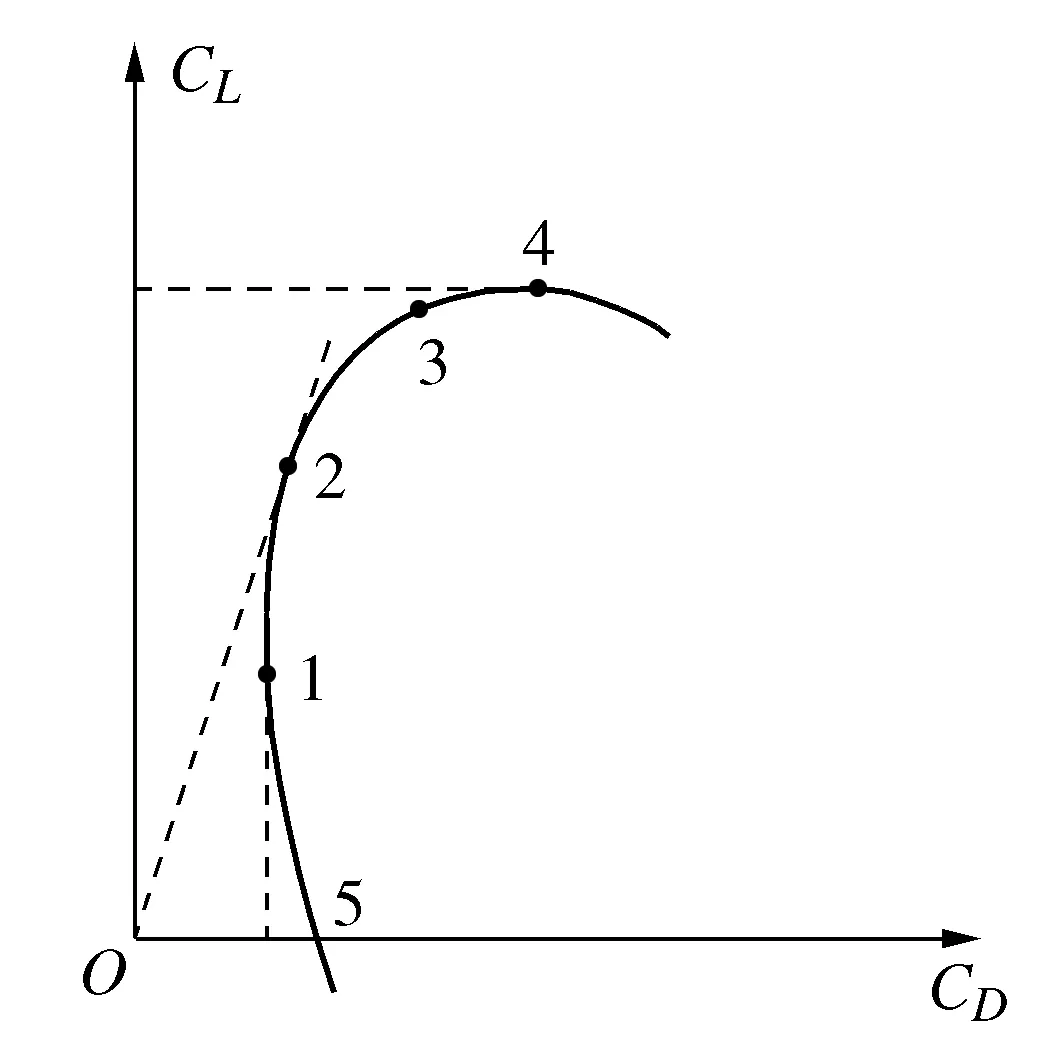
图4 翼型极线
用5次多项式分别对在Re=2.7×105、1.6×105、8×104下的CL和CD进行数据拟合,得到CLⅠ、CLⅡ、CLⅢ,当CL>0.4,拟合曲线满足CL和CD的变化趋势,分别如图5a)~图5c)所示[15]。
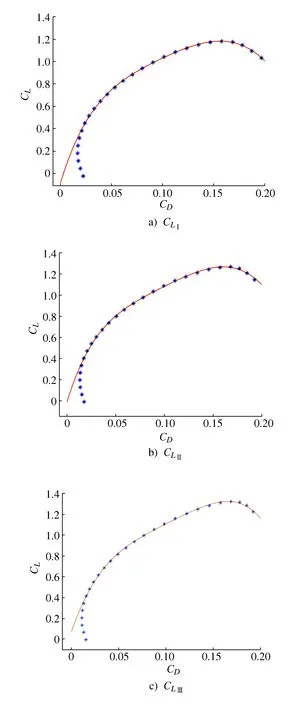
图5 CL与CD曲线拟合
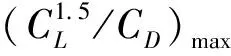
旋翼转速受到桨尖速度的限制,以避免叶尖出现过大的空气压缩效应,旋翼的叶尖速度不大于0.55 Ma。旋翼直径范围大概在200~700 mm, 对雷诺数的范围进行估算,则Re为8×104~2.7×105。
由于叶尖速度的限制,同时限制直径与转速,则要确保升力系数大于0.695。在当雷诺数从8×104增大到2.7×105,对应迎角为4.28°~4.953°。
在相同转速、反扭矩平衡状态时,上、下旋翼气动相互干扰,上、下旋翼的总距相差1°左右[16]。同时考虑电动马达和桨翼材料,上旋翼安装角取6°,下旋翼安装角取5°。
2.2 功率与半径、拉力
旋翼拉力[17]为:
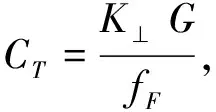
(4)
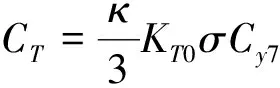
(5)
式中:K⊥为垂直吹风增重系数;G为旋翼推力,kg;ρ为所在海拔大气密度;Cy7为型阻升力系数;σ为桨叶实度;KT0为拉力修正系数;κ为叶端损失系数。
在悬停状态下,旋翼的需用功率为:
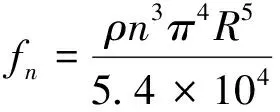
(6)
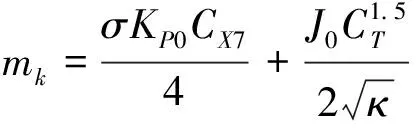
(7)
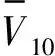
当桨叶数为6,则功率与半径、推力的关系:
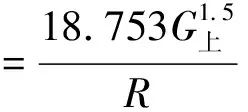
(8)
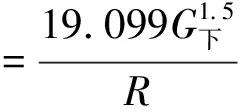
(9)
2.3 建立仿真模型
在扭矩平衡状态下,上、下旋翼分别为提供45%、55%的推力[18]。履带与混凝土壁面的摩擦系数为0.4,则上下旋翼推力和的0.4倍等于整机重量。
通过拟合电池电容量与重量的关系,联合式(8)、式(9),把机器人平台作业5 min所需的电容量转换为电池重量,建立闭合关系,输入旋翼的直径,输出整机的重量,如图6所示。共轴双旋翼的推力要大于机器人平台所需的正压力,则Dmin≥336 mm。
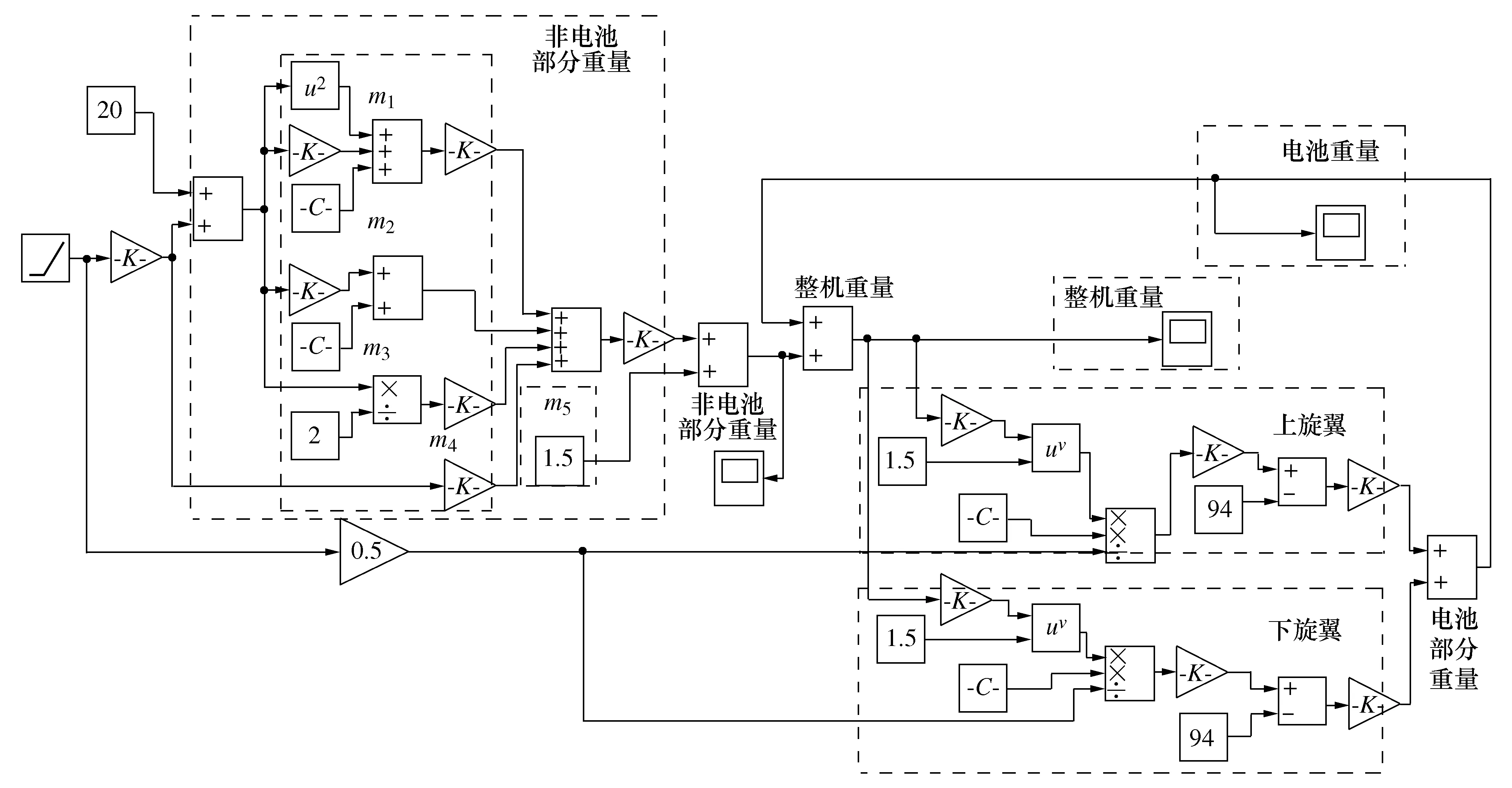
图6 仿真模型
3 结果与分析
如图7所示,横坐标为直径的增量,纵坐标为机器人平台部件的重量。机器人平台旋翼直径D从336 mm开始逐渐增大到700 mm。机器人平台的重量分为电池部分重量和非电池部分重量,电池部分重量G1随着直径的增大而减小,如图7a)所示;非电池部分的重量G2随着旋翼直径的关系接近于线性相关,如图7b)所示;机器人平台整体重量G随着直径的增大,先减小后增大,如图7c)所示。在D=376.4 mm处出现拐点,使机器人平台整机重量最轻=2.44 kg。
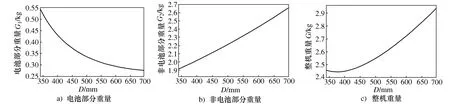
图7 重量与旋翼直径
如图7所示,随着旋翼直径的增大,机器人平台的重量也在增大,电池部分的重量反而减小。正如式(8)和式(9)所表达的关系,电池重量与旋翼直径成反比,与整机重量的1.5次方成正比。当旋翼直径继续增大,电池部分的重量先继续减小,在取得最小值后,一直增大。
机器人平台在优化前后的性能指标如表1所示。由于优化目的是在保证基本设计性能不变的前提下,对整机重量进行优化,所以机器人平台的行走速度、续航时间和负载能力未发生改变。当取得最优重量,整机重量较优化前减小了4.8%。同时,尺寸也发生了变化,长宽高分别减小了22.5%、23.8%、20.6%。机器人平台变得更加轻量、小巧和便捷,吻合优化预想。
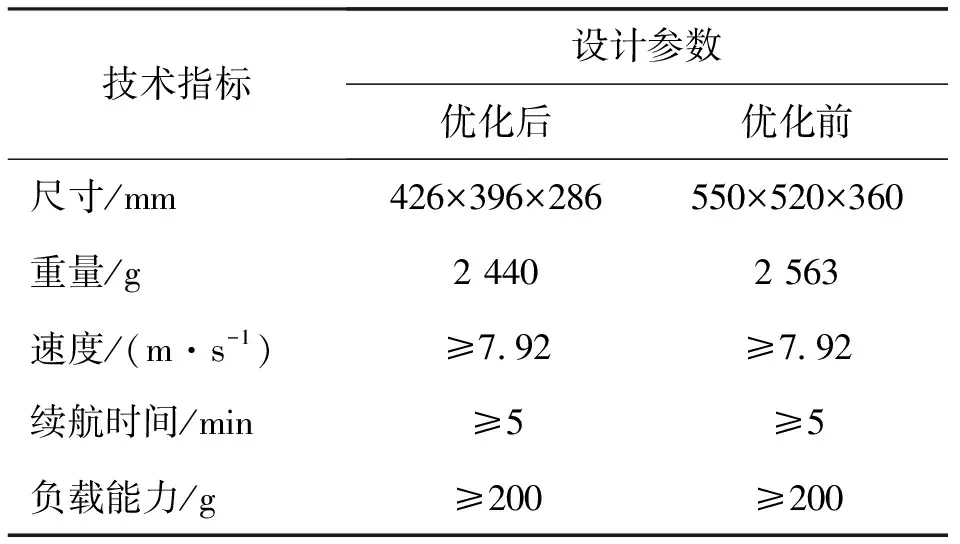
表1 机器人平台性能指标
4 结论
本文结合旋翼部分与机器人平台的整体重量,把空气动力学考虑到机器人平台对壁面正压力的设计之中,主要结论为:
1) 旋翼安装角的选择。一般翼型的安装角选择都考虑了多种飞行状态。由于机器人平台中的共轴式双旋翼只提供正压力,机器人平台就只有一个飞行状态——垂直悬停。本文根据自身结构的特点,求得“最经济状态点”后,确定安装角,设计旋翼,降低了能耗,减轻了整机重量。
2) 旋翼直径的确定。旋翼直径影响整个机器人平台的重量,同时,也影响共轴式双旋翼系统对机器人平台的正压力。本文推导了直径、整机重量和正压力三者的关系,搭建Simulink模型,在D=376.4 mm处求得最轻整机重量,为下一步的设计提供参考。
3) 本文对选定翼型进行2维的外流场计算,没有考虑机身和工况对旋翼诱导速度的影响,存在一定的误差。接下来,会根据实际工况,对机器人平台进行三维流场仿真。
