减阻航天煤油减阻机理与传热规律数值模拟
2022-03-15杜宗罡史雪梅单世群符全军张莉娟
杜宗罡,史雪梅,单世群,田 靓,符全军,张莉娟,吴 峰
(1. 西安航天动力试验技术研究所,陕西 西安 710100; 2. 西北大学 化工学院,陕西 西安 710069)
0 引言
随着我国运载火箭技术的不断发展,急需更大推力的火箭发动机,大推力液氧煤油发动机具有性能可靠、无毒无污染、价格相对低廉、推力和混合比可调节等优点,成为火箭运载器的发展重点。相应地,发动机再生冷却剂航天煤油的选型与设计,对于大推力液氧煤油发动机的技术开发与整体性能的提升至关重要。航天煤油在高速流经发动机组件时,受高流量、不规则湍流扰动影响会产生较大管路流阻,增加了泵后负载,使得涡轮泵功率和发生器温度提高,进而限制了发动机性能的进一步提升。鉴于此,相关研究部门开展了航天煤油流动减阻研究工作,取得了良好的减阻效果,但一定程度上降低了煤油的传热效率,传热效率降低可达30%。现有的有机物减阻剂主要有表面活性剂、聚异丁烯、烯烃聚合物等高分子聚合物,已应用于原油管道长距离输送领域,其中部分减阻剂不溶于航天煤油,部分减阻剂在航天煤油中使用时有一定减阻效果,但传热效率也显著降低。为了进一步推进减阻航天煤油工程应用,很有必要在已有航天煤油流动减阻实验研究的基础上,深入开展航天煤油减阻与传热过程的微观机理研究,在宏观连续介质的研究层面上找到航天煤油流动与传热的综合优化设计方案,进而提升发动机的综合工作性能。
尽管实验研究是目前获得航天煤油减阻与传热宏观规律的有效途径,但对于煤油流动与传热的微观详细数据分布及机理的合理分析尚有一定的距离。本研究工作基于Fluent15.0软件对含有烯烃聚合物减阻航天煤油及普通航天煤油在传热管内的流动与传热过程进行三维数值模拟,探究减阻航天煤油的减阻机理与传热弱化的机理,为改进减阻航天煤油减阻与传热强化过程提供理论基础与设计指导。
1 物理模型和计算方法
1.1 数学模型
为准确模拟减阻煤油与一般火箭煤油在直管道内的流动与传热过程,采用基于有限体积法的Fluent15.0求解器,描述其流动与换热的控制方程通用形式为
∇·(ρφ)=∇·(∇)+
(1)
不同变量的扩散系数具体形式如表1所示。

表1 不同变量所对应的φ、Γφ
采用RNG-epsilon湍流模型,动量方程、能量方程和湍流方程使用二阶迎风,压力与速度的耦合采用SIMPLE算法处理。应用增强壁面函数法处理壁面上的物理量与湍流核心区内待求未知量的相互联系,壁面函数法近壁面无量纲距离取值∈[30,300]。计算边界条件设定情况:壁面处取无滑移边界条件,进口设为质量流量进口边界条件,出口设为压力边界条件。
1.2 物理模型及验证
本文研究对象为文献[2]中火箭减阻煤油管路流动实验工况。因为在液氧煤油发动机中,推力室换热通道约为2 mm,前端部分管路约为10 mm。因此分别对管径为2 mm和10 mm工况下,传热管内减阻煤油与普通煤油的流动与传热过程进行模拟分析,圆直管长度为1.934 m。对照实验装置的设计尺寸,采用ICEM软件对该圆管进行三维建模和结构化网格划分,为了能够对煤油在圆管内的湍流流动进行精准分析,对壁面附近的网格进行了加密处理。设定管道流体流动方向为向,计算网格的截面如图1(a)所示,管道整体网格结构如图1(b)所示。
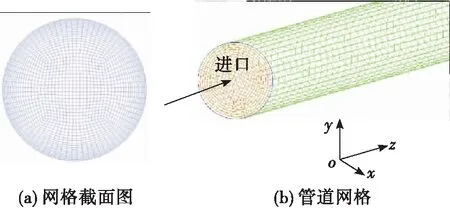
图1 物理模型及网格划分Fig.1 Physical model and grids
分别对管径为2 mm及10 mm两种传热管进行网格无关性计算分析,取距管道入口为=1 m处的绝对压力作为观测变量,其网格无关性分析规律如图2所示。
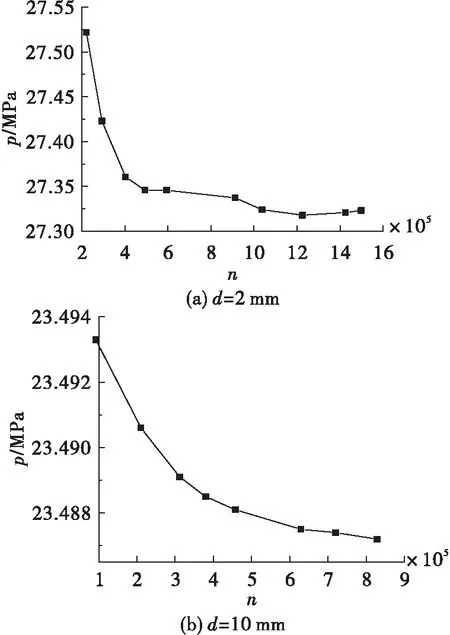
图2 计算网格无关性分析Fig.2 Test of grid size independency
由图2(a)可知,对于管径为2 mm情况,当网格数为1 036 980时,绝对压力趋于平缓,达到网格无关性要求,故采用网格数量为1 036 980作为计算网格。对于管径为10 mm情况,当网格数为629 377时绝对压力趋于平缓,达到网格无关性要求,故采用网格数量为629 377作为计算网格。
根据实验数据,减阻煤油的黏度为2.459 mPa·s,普通煤油的黏度为2.047 mPa·s。实验表明,添加聚合物减阻剂的减阻煤油其流动行为表现为非牛顿流体,非牛顿流体的黏度函数与应变速率或时间有关。参考文献[17],减阻煤油的黏度公式为
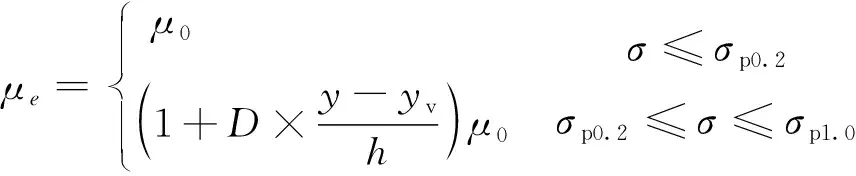
(2)
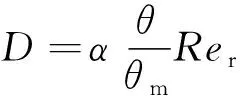
(3)
式中:为流体的动力黏度;为黏性底层的厚度;为减阻参数;为比例参数;为聚合物分子松驰时间;为溶液的松驰时间;e为雷诺数。
图3给出了速度边界层内无量纲速度的值敏感性分析,为流体黏度。
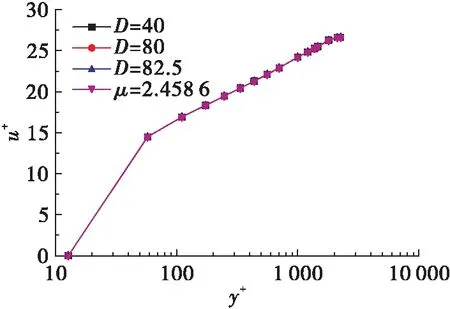
图3 不同D值对无量纲速度影响Fig.3 Effect of D on dimensionless velocity
由图3可知,在不同的值取值条件下,煤油无量纲速度分布规律与大小相差甚微,为方便模拟研究,选用文献[18]所推荐的=4。在管径为10 mm条件下,牛顿流体与非牛顿流体模型的数值模拟结果与实验数据的对比情况如图4所示。由图可知,非牛顿流体模型的模拟结果与实验数据的偏差整体小于牛顿流体,表明本文所采用的非牛顿流体数值模拟模型的合理性。
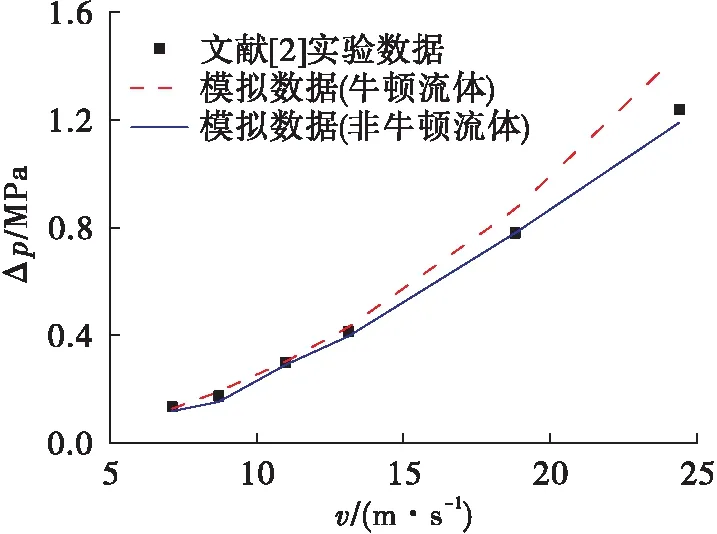
图4 两种模型模拟结果与实验数据对比Fig.4 Comparison between numerical simulation results and experimental results
1.3 模拟方法
本文主要应用雷诺平均方法(RANS)对减阻煤油进行数值模拟,使用文献[17]中所用UDF编译等效黏度模型,将壁函数加载到Fluent15.0软件上,采用解释型UDF,模拟减阻煤油的黏弹性特征。
2 计算结果及讨论
2.1 减阻机理
图5给出了在管径为10 mm,进口流速为24.4 m/s时,距进口=0.5 m处减阻航天煤油的轴流速度分布曲线。由图可知,减阻航天煤油(非牛顿流体)模拟的速度分布图与圆管内湍流截面速度分布规律相似,呈现出了对数分布规律。
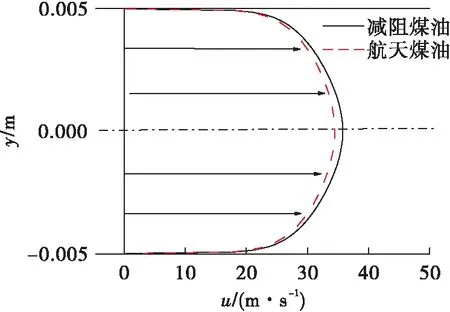
图5 煤油速度分布Fig.5 Velocity distribution of drag reduction kerosene
为进一步分析减阻航天煤油流动边界层内的速度分布规律,采用无量纲速度及无量纲距离描述速度与距离的依变规律。
=
(4)
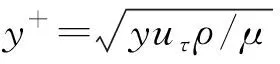
(5)
式中为摩擦速度。
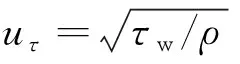
(6)
图6为管径=2 mm工况条件,在湍流充分发展段,普通航天煤油与减阻航天煤油管内无量纲速度随无量纲管径距离的变化情况。
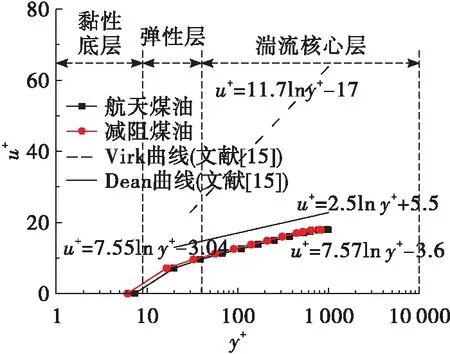
图6 无量纲轴向速度分布 (d=2 mm)Fig.6 Dimensionless axial velocity distribution(d=2 mm)
由图6可知,对于小管径流动情况 (=2 mm),减阻航天煤油与普通航天煤油的无量纲速度分布较为接近,减阻航天煤油速度数据基本上位于普通航天煤油速度数据之上。表明减阻剂的添加能够改变航天煤油边界层内速度分布规律,在一定程度上增加了湍流核心区的流速。
图7为管径10 mm条件下,管内减阻航天煤油与普通航天煤油无量纲速度对无量纲管径距离的变化规律。图7表明,对于大管径流动情况(=10 mm),湍流核心部分速度分布曲线明显向上移动了一段距离,湍流核心部分速度显著增大。在相同条件下通过的流量增加,实现了航天煤油流动的减阻增输,并与Virk渐近线趋势相同。在壁面湍流对数律区,减阻煤油模拟得到的无量纲速度剖面趋势与实验结果一致。综合图6和图7可知,由于加入高分子聚合物,减阻航天煤油流动边界层和过渡层都呈现出增厚的趋势,导致与普通航天煤油相比减阻航天煤油流动边界层弹性底层速度梯度降低,表现在速度分布曲线上,有明显的向上的偏移,速度变大。与普通航天煤油相比,实现了流量增加,达到了减阻效果。
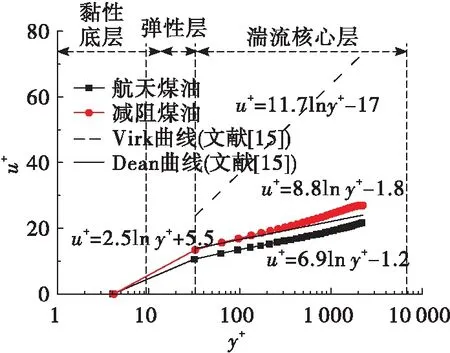
图7 无量纲轴向速度分布(d=10 mm)Fig.7 Dimensionless axial velocity distribution(d=10 mm)
定量分析减阻剂对航天煤油流动摩阻系数的影响规律,图8给出了在两种管径条件下,减阻航天煤油与普通航天煤油管内流动的摩阻系数对比。
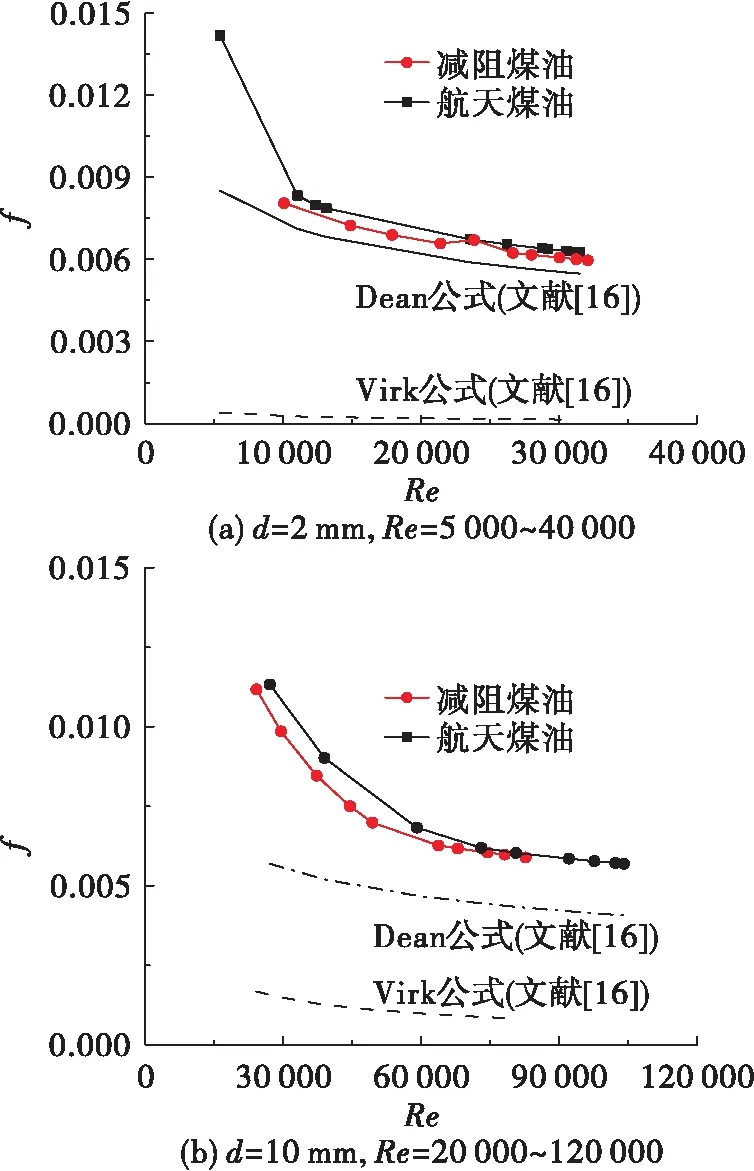
图8 摩擦阻力系数对比Fig.8 Comparison of friction coefficient
图8表明减阻航天煤油与普通航天煤油摩擦阻力系数值略大于Dean曲线,与Dean曲线趋势相同。由于减阻剂的添加,在相同雷诺数下,减阻航天煤油的摩擦阻力系数小于普通煤油,表明黏弹性添加剂在减阻流体的减阻效应中起正向作用,是导致减阻航天煤油具有湍流减阻效应的主要因素。
2.2 传热机理
为了验证传热模拟模型的合理性,所采用的模拟参数与文献[3]电传热实验工况一致,煤油流过电加热高温合金管道,管道外壁及进出口设置温度传感器,可获得管道的外壁温、煤油进出口温度。传热模拟的边界条件设置为:煤油进口温度30 ℃,出口压力15 MPa,流速为20 m/s,管壁热流密度10 MW/m。管道内壁温度随通道位置变化曲线如图9所示。
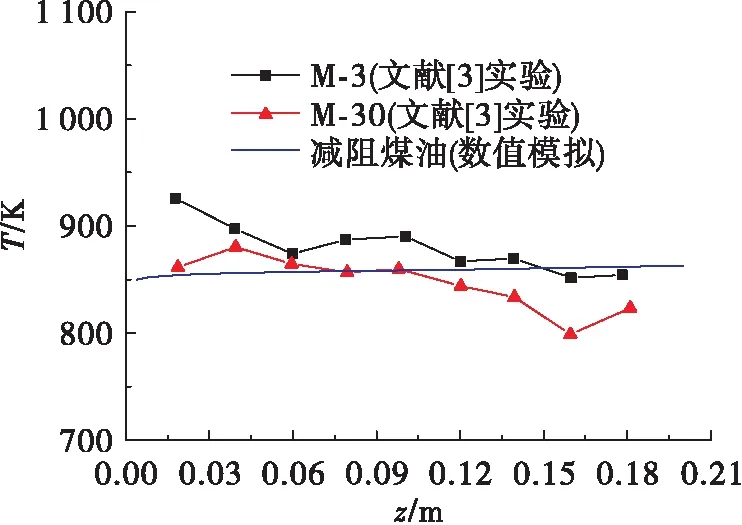
图9 管道内壁温度随通道位置变化曲线Fig.9 Profile of pipe inner wall temperature along channel position
图9表明,模拟结果与实验数据比较接近。在相同进口流速与热边界条件下,数值模拟与M-30实验数据的最大相对偏差为7.77%,模拟结果与文献实验结果较为吻合,说明本文采用的数值模拟模型具有一定的合理性。
图10给出了煤油在不同轴向位置其温度沿传热管径向的分布曲线。由图可知,在不同轴向位置的煤油温度径向分布曲线中,普通航天煤油的温度要高于减阻航天煤油,即普通航天煤油管内温升高于减阻航天煤油,表明传热管内普通航天煤油的传热效率优于减阻航天煤油。
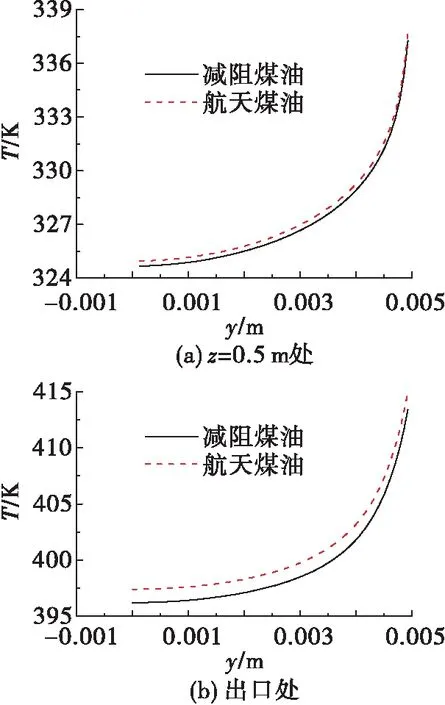
图10 不同轴向位置煤油温度径向分布Fig.10 Radial distribution of kerosene temperature at different axial positions
为深入研究分析减阻航天煤油传热机理,需进一步定量分析煤油传热过程中,其管壁附近的温度边界层厚度随流动方向的发展与变化规律。通常规定流体与壁面之间的温度差(-)达到最大温度差(-)的99%,此时垂直于管壁的向距离定义为温度边界层厚度,即
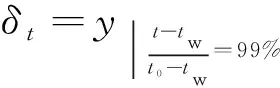
(7)
图11给出了不同管径下,传热管内普通航天煤油与减阻航天煤油温度边界层厚度沿流动方向的发展曲线。由图可得,减阻航天煤油的温度边界层厚度大于普通航天煤油温度边界层,随着流动的发展,两者温度边界层厚度的差异增大,且传热管径越大,现象越为显著。依据传热学的理论分析,温度边界层越厚,表明对流传热的热阻越大,传热效果越差,进而降低了减阻航天煤油传热速率,产生传热弱化现象。
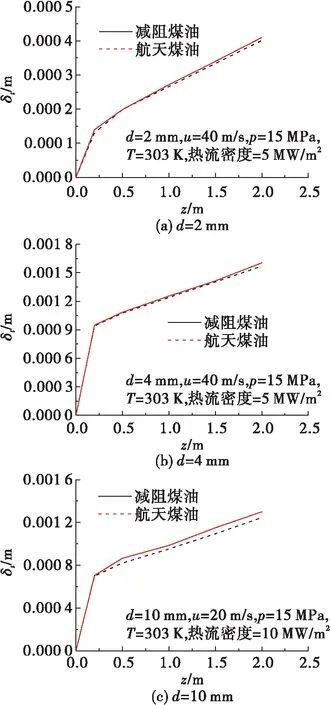
图11 温度边界层厚度沿流动方向发展规律Fig.11 Thickness of temperature boundary layer along the flow direction
对管内煤油的对流传热过程进行进一步无量纲温度分析,无量纲温度的定义为
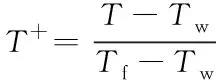
(8)
无量纲距离的定义为
=
(9)
图12给出了传热管内煤油无量纲温度沿壁面距离分布规律。由图可知,流体温度越高,其无量纲温度越小,从图中的温度分布来看,温度分布曲线越靠下,其传热效果越好,表明普通航天煤油的传热效果优于减阻航天煤油。
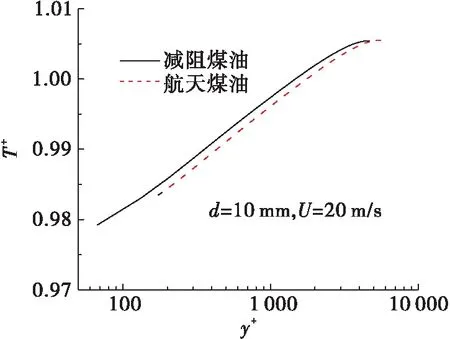
图12 无量纲温度T+沿壁面距离y+分布规律Fig.12 Distribution of dimensionless temperature along dimensionless distance of wall
3 结论
1)减阻剂的添加使得减阻航天煤油流动边界层的过渡层呈现出增厚的趋势,导致弹性底层速度梯度降低,增加了湍流核心区的流速,即实现了航天煤油流动的减阻增输效应。
2)减阻航天煤油的摩擦阻力系数小于普通航天煤油,黏弹性添加剂在减阻效应中起到了正向作用,是导致减阻航天煤油具有湍流减阻效应的主要因素。
3)普通航天煤油传热管内的温升高于减阻航天煤油,减阻航天煤油的温度边界层厚度大于普通航天煤油的温度边界层,增加了减阻航天煤油管内的传热热阻,降低了减阻航天煤油的传热速率。
4)可进一步通过研究分析,减阻剂混合、减阻剂分子量设计的优化分析,找到减阻与传热强化两者矛盾的有效协调方法,进而实现减阻与传热的优化设计。
