RBF神经网络整定参数的预测滤波PID控制
2022-03-14侯小秋
侯小秋
(黑龙江科技大学 电气与控制工程学院, 黑龙江 哈尔滨 150022)
PID控制结构简单、易于实现,并且控制效果较好,因此,目前运行的控制系统90%以上采用常规PID控制。但当被控对象系统具有非线性和时变性时,常规PID控制难以达到良好的控制效果,因此随着神经网络理论的不断发展,研究基于神经网络的PID控制方式具有重要的现实意义。
文献[1-5]研究了神经网络PID控制的典型算法。文献[1]研究了基于径向基函数(Radial Basis Function,RBF)模糊神经网络的PID控制参数的自整定算法,RBF模糊神经网络的参数先应用遗传算法进行粗调,达到一定的预定精度后,使用BP神经网络提高精度,解决了常规PID控制和模糊PID控制的控制精度差、无自适应和模糊规则很难确定的问题;文献[2]改进了传统RBF神经网络的结构,构建了动态自适应RBF神经网络的PID控制算法;文献[3]提出了基于RBF神经网络的智能PID控制算法,在常规PID控制器中引入Smith预估器,针对纯滞后对象提出了一种智能控制算法;文献[4]研究了采用遗传算法优化的RBF神经网络整定PID参数的算法,收敛速度快;文献[5]提出了一种基于RBF神经网络的多步预测的自适应PID控制算法。已有的研究大多是针对PID控制的,不是针对预测滤波PID控制的,基于预测滤波PID控制的研究鲜有报道。文献[6]研究了在线修正参数的随机NARMAX模型的具有预测滤波的PID控制,其优点是具有在线修正PID参数的性能,缺点是需要辨识随机NARMAX模型;文献[7]研究了在线修正参数的确定性多变量NARMAX模型的具有预测滤波的PID控制,同样具有文献[6]的优缺点;文献[8]研究了变时滞无模型的在线修正参数的预测滤波PID控制,适用于难以建立模型的变时滞非线性系统的控制,并对PID参数进行在线修正,只要给定一个有效的初始PID参数,在修正算法的作用下,PID参数向系统运行性能优良收敛。
本文针对预测滤波PID控制,采用直接极小化指标函数自适应算法,提出新的RBF神经网络的输出权和节点中心及节点基宽参数的在线学习算法,研究RBF神经网络整定参数的预测滤波PID控制问题。
1 RBF神经网络辨识器
1.1 辨识器
RBF神经网络结构如图1所示,是一种三层前向网络。

图1 RBF神经网络结构图
图1中xT=(x1,x2,…,xn)为输入向量,n为输入层单元数,TT=(h1,h2,…,hm)为隐层节点径向基向量,m为隐层单元数,hj为径向基函数(RBF),wi为输出加权,ym为辨识器输出。
径向基函数hj为高斯函数:
(1)
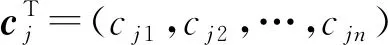
辨识器输出:
ym=w1h1+w2h2+…+wmhm=wTT,
(2)
式中wT=(w1,w2,…,wm)为权向量。
1.2 ym关于待学习参数的梯度表达式
RBF神经网络辨识器待学习参数向量η为
式(2)两边分别对wj、cji、bj求偏导,可得
(3)
(4)
(5)
1.3 ym关于η的二阶导数矩阵表达式
式(3)两边分别对wi、cli(l≠j)、cji、bl(l≠j)、bj求偏导,可得
(6)
(7)
(8)
(9)
(10)
由式(4)可得
(11)
式(4)两边分别对cji、clp(l≠j)、cjp、bl(l≠j)、bj求偏导,可得
(12)
(13)
(14)
(15)
(16)
由式(5)可得
(17)
(18)
式(5)两边分别对bl(l≠j)、bj求偏导,可得
(19)
(20)
1.4 RBF神经网络在线学习算法
将文献[6]的直接极小化指标函数自适应算法改进后应用,实现RBF神经网络参数的在线学习算法,指标函数为
(21)
式中g*(…)为目标函数,y(t)为实际输出。
则η的学习算法为
(22)
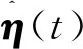
(23)
式中λ(t)为权重对角矩阵。
式(22)的矩阵Q(t)求逆及式(23)克服算法病态的权重对角矩阵λ(t)的确定可参考文献[9]的算法。
2 PID控制参数的在线整定算法
文献[6]的增量式预测滤波PID控制为
(24)

神经网络整定参数的指标函数为
(25)
式中E(t)为指标函数。
h、s0、s1、s2的调整采用梯度下降法[10]:
(26)
(27)
(28)
(29)

xT=(u(t-d),…,y(t-1),…),
则x1=u(t-d),由式(2)可得
(30)
3 仿真研究
被控对象
参考输入
PID控制参数初始值
h=0.1,s0=0.09,s1=-0.01,s2=0.004。
RBF神经网络结构为2×4×1,输入层
x1=u(t-4),x2=y(t-1),
初始参数
c11=0.1,c12=0.1,w1=0.31,b1=1,
收敛因子
Hessian矩阵初始值
Q(0)=100I,
控制输入的饱和限幅Umax=0.6。
采用MATLAB7语言编程仿真,给出系统输出y(t)的响应曲线(图2)。图2(a)为无参数整定的响应曲线,跟随性能差,跟随偏差大;图2(b)为有参数整定的响应曲线,跟随性能良好,初始时动态超调较大,是由于初始时PID控制参数还没整定好导致。图3给出了PID控制参数的整定曲线。图4给出了RBF神经网络的输出权和节点中心及节点基宽参数的在线学习的优化曲线。
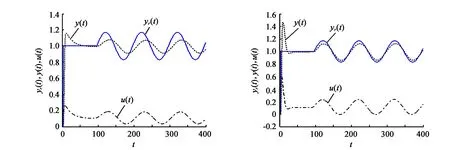
(a)无整定 (b)有整定

图3 PID控制参数的整定曲线

图4 RBF神经网络参数的优化曲线
4 结论
(1)RBF神经网络结合预测滤波PID控制进行控制算法研究,提出了基于RBF神经网络辨识的在线整定预测滤波PID控制参数的算法;
(2)理论推导出RBF神经网络辨识器输出关于RBF神经网络参数的梯度表达式和二阶导数矩阵表达式;
(3)采用直接极小化指标函数自适应算法,实现了RBF神经网络参数(输出权和节点中心及节点基宽参数)的在线学习算法;
(4)仿真研究表明,提出的智能PID控制算法具有响应速度快、超调小和跟随性能好,无静态偏差的性能,优于常规PID控制。
