一种高g值压阻式加速度传感器仿真设计及优化

杨雨君， 王 鹏， 张昌明， 杨 帆， 陈芳芳

(陕西理工大学 机械工程学院， 陕西 汉中 723000)

微机电系统(Micro-Electro-Mechanical System，MEMS)技术由微纳米技术发展而来，是对微纳米材料进行设计、加工、制造和控制的技术，具有微型化、易集成化、易批量生产、多学科交叉等特点[1-2]，是21世纪高新技术之一。MEMS高g值加速度传感器最先研究是基于军事需求，在爆炸侵彻特殊领域中监测瞬间的加速度值，后应用到冲击碰撞测试中，近年来因为测试情况复杂多变，侵彻武器需要检测多方向的加速度，在冲击碰撞中也不再是单方向碰撞，单轴的传感器逐渐不能满足要求，需要能检测多方向的加速度传感器[3-4]。

在高g值加速度传感器研究方面，Endevco公司为美国军方研制的7270A高g值加速度传感器性能优越，广泛应用在美军导弹引信中，量程最高达2.0×105g[5]；美国国家航空航天局为满足高电磁场环境，研发出一款单晶6H-SiC压阻式加速度传感器，量程为1.0×105g，同时固有频率和灵敏度性能都极好[6]；中国电子科技集团公司第十三研究所设计了一种应用于多领域的压阻式传感器，采用八梁结构对其进行性能测试，灵敏度为1.52 μV/g，固有频率在200 kHz以上，量程为1.5×105g[7]；浙江大学与中国科学院上海微系统与信息技术研究所设计的一种压阻式加速度传感器，整体结构采用对称的双悬臂梁，设计量程1.0×105g，可应用于抗过载保护[8]。上述传感器测量方向均为单轴检测，加速度方向改变，传感器就不能有效工作。

针对当前高g值测试难度增高的问题，本文设计了一种高g值加速度传感器，其结构能同时满足水平面内相互垂直的两个方向的加速度测量，并利用有限元对传感器进行仿真分析和结构优化，验证了结构的可行性与可靠性。

1 传感器工作原理与结构设计

1.1 工作原理

压阻式加速度传感器的工作原理是利用半导体材料的压阻效应来测量加速度，给半导体材料施加一轴向外力，半导体材料的晶体结构产生形变，晶体中电子迁移率和载流子密度产生改变，则材料的电阻率发生变化[9]。它的使用方法是将半导体敏感条粘贴在被测物体上，随被测件的应变，其电阻发生相应的变化。半导体敏感元件产生压阻效应时，其电阻率的相对变化与应力间的关系为

(1)

式中π为半导体材料的压阻系数，σl为纵向应力，σt为横向应力，Δρ/ρ为电阻率的相对变化率。

1.2 传感器结构设计

本文设计的高g值加速度传感器以传统的质量块-梁结构为基础。如图1所示，质量块居于中心，增强对外界信号的响应，四周为8根梁，梁结构使用主副梁结构，边框的4条边分别由2根梁连接，分为支撑梁和敏感梁。支撑梁负责支撑质量块，其厚度与质量块相等，提高固有频率和增强加速度传感器的抗过载能力；敏感梁厚度较薄，其上需要制作压敏电阻，形成惠斯通电桥，将敏感梁应力变化转换为电压变化，从而达到测量加速度的效果。

图1 压阻式加速度传感器结构示意图

该加速度传感器结构简单，加工难度低，成本低廉，适用于高g值冲击加速度的测量。表1为传感器现有的设计参数，此时传感器的设计量程是1.5×105g，抗过载值是2.0×105g，一阶固有频率为110.8 kHz。

表1 高g值压阻式加速度传感器几何尺寸

2 传感器静态仿真分析

2.1 静态仿真分析

静态仿真分析是指在方向与大小都不变的载荷作用下，同时在不考虑惯性和阻尼的情况下，研究结构或部件的位移、应力、应变等。而对MEMS高g值加速度传感器进行静态仿真，主要是满量程作用下结构的位移分布和应力分布[10]。

2.2 仿真模型设置

应用ANSYS软件对传感器结构进行仿真分析，在Geometry模块中建立有限元三维模型。传感器的整体结构材料采用硅，材料特性见表2。硅是性能优异的半导体材料，其导电性好，弹性模量适中，加工成微米级别后，屈服强度上升，可以应对较高冲击加速度，所以用硅作传感器结构的加工材料[11]。

表2 材料特性

在对传感器结构进行网格划分的过程中，采用结构化的网格，实现区域的边界拟合较简单，同时网格生成速度快且质量好[12]。在网格划分时网格单元是数值模拟的基础，网格划分直接影响仿真结果，网格单元尺寸的大小影响计算精度，网格的数量决定仿真计算规模，即网格尺寸越小，网格数量就越多，则计算精度越高，计算规模会加大，因此在确定网格划分时，要同时考虑计算精度和计算规模这两个因素[13]。在对建立的模型进行网格划分时，质量块不进行变形分析，网格划分较疏，可减少运算时间，如图2的区域1所示；敏感梁的网格划分较密，可提高计算精度，如图2的区域2所示。

图2 网格划分图 图3 载荷和约束图

最后对模型添加载荷和约束，根据实际情况，将传感器的8根梁与边框的连接处设置为固定约束面，如图3所示，A为添加的载荷，B、C、D、E、F、G、H、I为固定约束面。

2.3 仿真结果分析

在对加速度传感器结构仿真分析时，最大应力值是一个重要参考指标，在满量程1.5×105g输入下，若结构产生的最大应力值过小，则灵敏度会较低，即使在后处理时接入放大电路，其测量的数据失真也会加大；若结构产生的最大应力值过大，在测量过程中极易出现疲劳损伤甚至断裂现象，寿命会大大降低，所以合理选择应力值较为重要。如图4所示，在满量程1.5×105g情况下，得到传感器结构等效应力云图，该结构的应力集中区域是梁和边框的连接部分，最大应力值约为231.42 MPa，远小于硅的许用应力340 MPa，该结构在满量程范围内可以安全工作。图5所示为等效位移云图，可以看出，该结构最大位移区域在质量块处，最大位移值为0.7 4 μm，传感器在小位移内便得到较大的应力，说明结构具有可行性。

图4 应力云图 图5 位移云图

3 传感器动态仿真分析

3.1 瞬态动力学分析

在动态分析时使用瞬态动力学仿真分析，又称为时间历程分析，其载荷是随时间变化的，可以分析结构在静载荷、瞬态载荷、正弦载荷等任何类型载荷作用下的位移、应力和应变响应，因此相较于其他动态分析类型，瞬态动力学分析更符合真实情况。瞬态动力学分析法常用的有完全法、减缩法和模态叠加法3种[14]。

3.2 仿真模型设置

在进行瞬态动力学仿真分析时，加速度传感器结构所用的三维模型、划分网格、固定约束同静态仿真分析相同。分析方法选用完全法，结构施加的载荷为正弦加速度，如图6所示，峰值约为1.5×105g，时间为1 s。

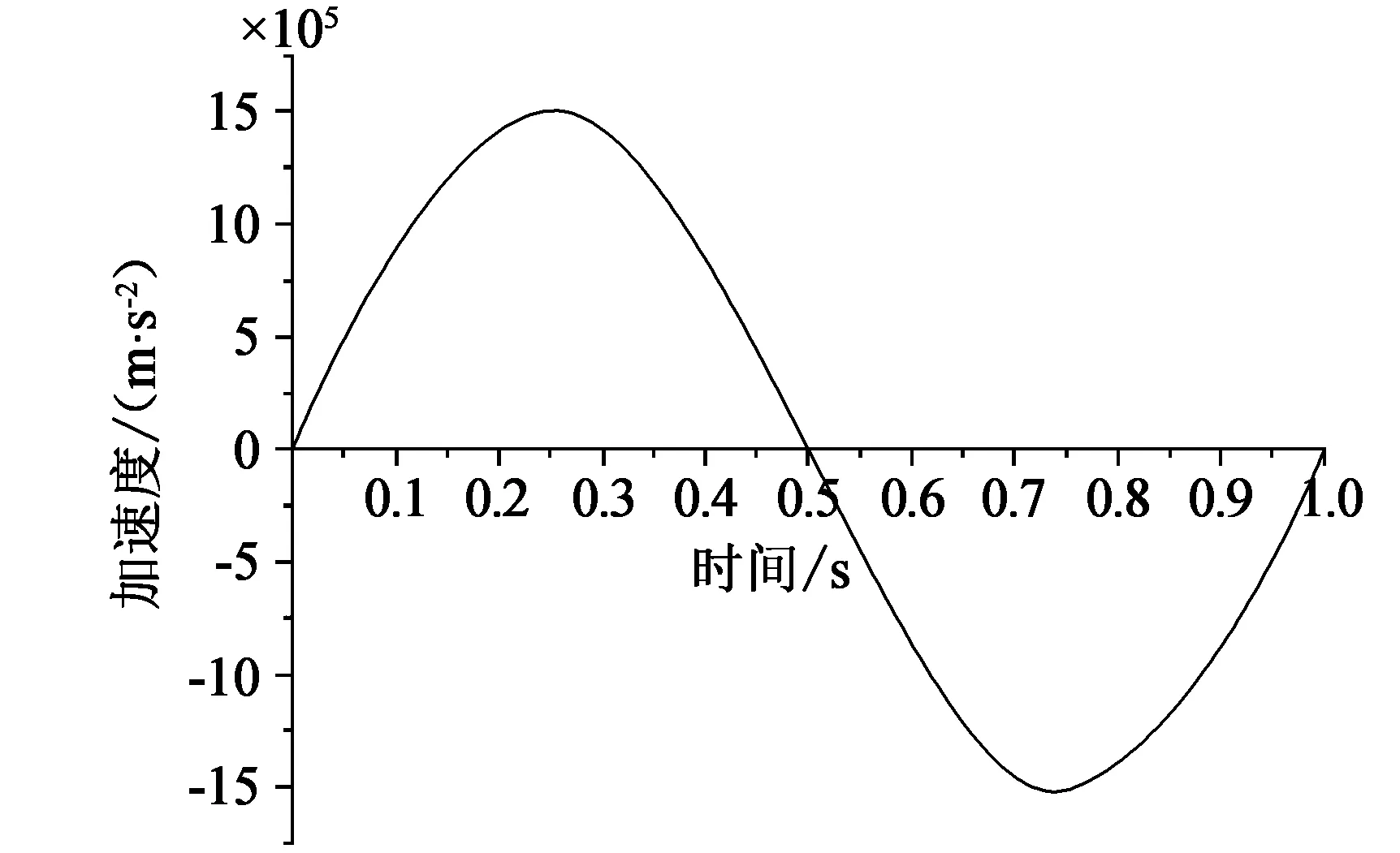
图6 正弦载荷变化图

3.3 仿真结果分析

对分析结果进行后处理，得到应力曲线和位移曲线如图7和图8所示。由图7可以得出，在动态响应过程中，在0.5 s处应力变化从正到负，对应图6此时加速度方向改变，在0.25 s和0.75 s时达到最大应力值，对应图6此时加速度为满量程1.5×105g，在整个应力变化过程中，都小于硅的许用应力340 MPa，可以正常工作。由图8得出，在整个正弦载荷变化过程中，在0 s和1 s处加速度为0，位移最小值接近0；在0.5 s时加速度改变方向，位移曲线变化也从正到负；在0.25 s和0.75 s时加速度为1.5×105g，位移达到最大值0.8 μm。上述对结构的瞬态动力分析说明该结构设计合理可靠。

图7 应力曲线 图8 位移曲线

4 优化设计

4.1 优化方法

响应面法的多目标优化方法操作简单，机器运算，优化可靠，广泛运用在模拟和系统动力学中，因此选择响应面法多目标优化作为本结构的优化方法。利用回归分析、最小二乘法对数据进行拟合，通过计算机运算，可以建立复杂的多维空间曲面模型。最后使用MOGA算法求解并筛选最优解[15]，其优化变量与优化目标之间的函数关系为

(2)

式中y为优化目标，X=(x1,x2,…,xi,…,xk)为优化变量，β为方程的回归系数。

4.2 优化参数设计

由模型分析可知，传感器结构有质量块的长、宽、厚3个参数，支撑梁的长、宽、厚3个参数，敏感梁的长、宽、厚3个参数，其中质量块厚度与支撑梁厚度相等，敏感梁长度和支撑梁长度相等，为了保证传感器X和Y方向(见图1)具有相同的性能，质量块长和宽相等，所以其独立参数有6组。选择质量块长(宽)、厚，支撑梁长、宽，以及敏感梁宽、厚共6组参数作为优化变量，以结构的最大变形量和最大一阶固有频率作为优化目标参数，表3所示为优化设计参数。根据选定的优化变量和优化目标参数设计实验，生成优化样本点。

表3 优化设计参数

4.3 优化分析

根据优化变量与优化目标之间的函数关系，可以获得各变量对最大应力和一阶固有频率的灵敏度影响，如图9和图10所示。从图9中可以看出，在优化范围内，参数P1、P3、P4、P5和最大变形呈正相关性，P6和最大变形呈负相关性，P2对最大变形基本无影响；由图10可以看出，参数P1、P3、P4、P5和最大变形呈负相关性，P6和最大变形呈正相关性，6个参数对一阶固有频率的影响与最大应力相反，说明结构设计中最大应力和一阶固有频率是一对矛盾的设计目标，在优化时要保证二者同时达到相对最优。

图9 最大应力与灵敏度分析 图10 一阶固有频率与灵敏度分析

在建立的响应面模型上，选择多目标遗传算法，在最大应力200～250 MPa和一阶固有频率≥100 kHz条件范围内，对结构进行优化求解，根据运算规模与实际情况需要，选择计算生成100个优化样本点。图11所示为100组样本图，从生成的样本中筛选出一阶固有频率和最大应力同时达到较优的3组作候选点，以原始数据点为参考点，得到表4。

图11 样本图

表4 优化候选点

经过对比分析，取候选点2各参数并圆整作为最优设计方案：P1为2425 μm，P2为500 μm，P3为50 μm，P4为100 μm，P5为50 μm，P6为490 μm，再次对传感器结构进行仿真分析，获得优化后结构的最大应力和一阶固有频率，如图12和图13。与传感器原结构即参考点的数据相比，最大应力由231.2 MPa上升到237.13 MPa，最大应力增大了2.6%，灵敏度得到一定提高；一阶固有频率得到了极大提升，由110.6 kHz上升到145.42 kHz，增大了31.5%，加快了传感器的响应时间，优化后传感器的性能得到了有效提升。

图12 优化后等效应力云图 图13 优化后一阶固有频率图

5 结论

本文设计了一种用于测量高g值的加速度传感器结构，通过ANSYS建立三维模型，分析了该结构的静态特性和动态特性，验证了该结构的合理性和可行性，在满量程1.5×105g加速度时，结构能满足高g值环境下的测试需求；利用多目标响应面法对结构进行了优化，一阶固有频率提高了31.5%，最大应力值增大了2.6%，为传感器的制造加工奠定了理论基础。在后续研究中还需对优化后的传感器结构展开试验，考虑到实际应用环境的复杂性，还需进一步对传感器结构的阻尼特性进行研究。