双螺杆空压机壳体声辐射特性分析
2022-03-14何亚银肖聪聪赵永强
何亚银, 肖聪聪, 赵永强, 王 凯, 张 炜
(陕西理工大学 机械工程学院, 陕西 汉中 723000)
双螺杆空压机主要噪声来源为结构振动噪声、气流脉动噪声和电动机噪声等,而空压机产生的结构振动所辐射出的噪声是最重要的噪声源。在空压机内部,双螺杆转子在啮合过程中,激发出各种脉动压力和脉动力,向压缩机壳体的壁面辐射从而产生噪声。这些振动产生的噪声会对空压机的壳体及其附属零件造成损害,分贝过高的噪声对人的健康也有不同程度的损害。因此,对双螺杆空压机进行振动声学特性分析,研究振动声学之间的规律,是降低空压机噪声的重要途径。
在双螺杆空压机振动声学特性方面,国外学者Rane等[1]介绍了螺杆压缩机的动网格划分,列举了计算流体力学(Computational fluid dynamics,CFD)求解方法的应用。Andrews等[2]则在实验室测量了不同负荷下半封闭制冷螺杆压缩机声强、声功率和气流脉动,给出了气流脉动随排气压力变化的规律。Fujiwara等[3]对螺杆压缩机的振动噪声进行了比较全面的测量,并对有问题的压缩机单独测试,提供了宝贵的数据。Victor[4]使用有限元仿真方法对双螺杆挤出机的流场进行了分析,并与实验结果对比验证,分析了产生误差的原因。Sangfors等[5]对辨识螺杆压缩机主要的振动噪声源开展了大量的研究工作,指出处于气流脉动基频及其整数倍频率的振动噪声值较大。国内学者沈久兵等[6]通过对半封闭螺杆制冷压缩机排气噪声数值模拟与测量结果验证,进一步分析了压缩机排气流道优化设计对气流脉动和噪声的影响。季晓明等[7]通过改变压缩机壳体的不同参数研究了壳体噪声辐射的影响,并得到了有效降低壳体噪声辐射的方法。王小明等[8]通过改变平衡式双螺杆转子的齿顶间隙与频率,研究得到齿顶间隙为0.1 mm时平衡式双螺杆压缩机产生的噪声最小。陈文卿等[9]针对半封闭变频螺杆制冷压缩机,通过试验研究验证了排气端面脉动衰减装置和排气管路消声器两种降噪方法的有效性,结果表明压缩机平均降噪结果随转速增加而增强。柯李菊等[10]针对单一腔型声学覆盖层低频隔声性能和耐压性能较差的特点,将仿真与前人试验相结合,得到了声学覆盖层的空腔体积越大,低频段的隔声性能越好,中、高频段的吸声性能变差。王军利等[11]针对双螺杆压缩机工作过程中转子的结构特性问题,通过有限体积法求解压缩机工作过程中产生的压力场和温度场,得到了温度场是螺杆转子产生较大变形和应力的主要原因。程双灵等[12]通过降低压缩机噪声源与提高隔声罩的吸、隔声效果两方面来控制螺杆压缩机的噪声,研究了排气止回阀对压缩机噪声的影响,对隔声罩结构和吸声材料进行了改进设计。李双等[13]研究表明构成总辐射声功率的n阶声辐射模态中,起主导作用的仅仅是前几阶模态。王小明等[14]基于平衡式双螺杆压缩机提出了一种充分体现其轴向力平衡为优势结构特征的平衡式双螺杆压缩机支撑件的结构形式,可为平衡式双螺杆压缩机支撑件的精确设计及其性能的再优化提供理论依据。徐俊伟等[15]从气动声学基本理论出发,通过应用实例说明三种气动噪声数值方法在求解过程中的优缺点,可对气动噪声的预测提供一定的参考依据。
综上所述,对于螺杆压缩机的研究侧重于结构特性及脉动气流噪声的研究,而将压缩机壳体模态分析与声学模态相结合的分析较少。本文采用双螺杆压缩机壳体模态分析得到压缩机壳体频率范围,再将模态得到的频率范围作为条件,来实现压缩机壳体压力声学特性分析,以期获得压缩机壳体表面声压与声压级的分布规律。
1 计算方法
1.1 结构模态分析理论基础
模态分析是振动分析方法之一,对于一个多自由度系统,其整体动力平衡方程[16]为

(1)

分析结构固有模态是分析结构的固有动力学特性,与结构所受载荷形式无关,其目的是得到结构固有频率和相应的模态振型,模态分析是在施加零位移约束的前提下,求解结构的固有频率及相应的模态振型,方程[17]为

(2)
1.2 声学模态分析的基础及方法
有限单元分析方法的声学流体矩阵方程:
(3)


(4)
其特征方程为
(5)
应用数值计算方法对上述特征方程(5)求解计算,其求得的结果便可以得到在不同的场边界条件下空压机壳体的模态频率以及模态振型,其中,模态频率即为声场的声学共振频率ωi(i=1,2,…,n),而模态振型即为声场的声压分布Pi(i=1,2,…,n)。先建立空压机壳体的声腔模型,本文不对其设置任何约束,即让空压机壳体声腔自由振动,分析所得刚性壁空压机壳体声学模态。而后,再利用声压与声压级转换公式计算出声压级,计算公式为
(6)
式中LP为声压级,P为声压,P0为基准声压,在空气中P0=2×10-5Pa。
2 有限元模型建立
2.1 模型建立及网格划分
利用建模软件UG对双螺杆空压机壳体建模,如图1(a)所示,并通过相应格式转换后导入COMSOL中。由于模型存在大量曲面且结构复杂,因此选用非结构化的四面体结构,尺寸控制用边界层控制,对重点考虑的曲面与边进行加密处理,防止畸形网格过多及负体积的出现而导致计算精度不够和不收敛情况出现,最终得到453 674个网格单元、95 870个网格节点、76 256个边界元和7694个边单元。双螺杆空压机壳体网格模型如图1(b)所示。最后对网格进行质量测量,通过偏斜度对声学模型进行网格评估,结果表明网格质量符合计算要求。

(a)壳体三维实体简化模型 (b)壳体网格模型
2.2 边界条件及求解设置
对于双螺杆空压机壳体的结构模态材料设为结构钢,弹性模量为2.1×1011Pa,泊松比为0.3,密度为7800 kg/m3。
针对结构的模态设置,对壳体施加约束,由于系统的固有模态与系统所受载荷无关,只需要对壳体底部施加固定约束,而且由模态分析相关理论可知,在结构振动过程中起主要作用的是低阶模态,而高阶模态影响较小,且下降速度很快,所以将模态数目设置为六阶。而对于声学模态设置,材料选择空气,密度为1.413 kg/m3,温度设为298.15 K,压强设为1个标准大气压,声速设为340 m/s。假设声音在壳体腔内传播,壳体壁面为完全反射声场,特征频率数与基准值根据结构模态结果的频率范围设定,声场边界设为硬声场边界,得到结构模态的仿真结果后,只需要得到结构模态分析的频率范围,将结构模态分析的频率范围作为声学模态特征频率的研究范围,最后结合结构模态与声学模态之间的联系,分析对壳体的声压和声压级分布云图及规律。
3 仿真结果分析
3.1 壳体声压及声压级分布情况
通过有限元分析软件ANSYS对双螺杆空压机壳体进行结构模态分析,可以得到其前六阶模态频率分别为716.3、1 102.8、1 514.4、1 994.1、2 581.5、2 857.3 Hz。再通过仿真软件COMSOL中压力声学模态分析得到双螺杆空压机壳体声学模态结果,由于在结构振动分析中得到双螺杆空压机壳体模态激振频率范围为700~2900 Hz且为前六阶,因此本文选取声学模态特征频率的前六阶和与结构模态激振频率接近的声学振型,结果如图2—图7所示。

(a)总声压 (b)声压级

(a)总声压 (b)声压级

(a)总声压 (b)声压级

(a)总声压 (b)声压级
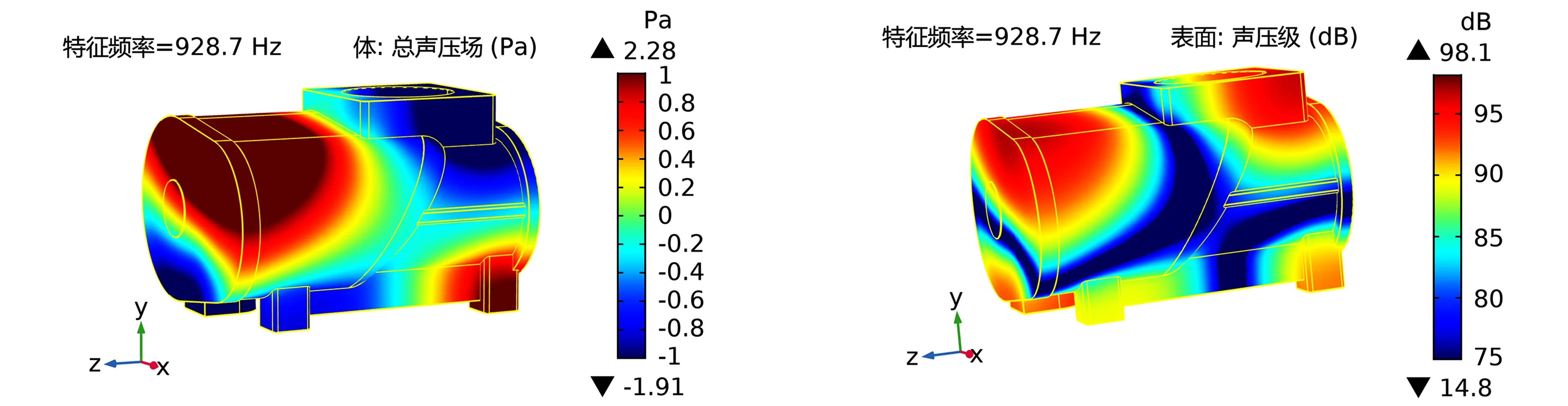
(a)总声压 (b)声压级

(a)总声压 (b)声压级
在分析双螺杆空压机壳体声学模态时,选取前几阶作为分析对象。由于本文要考虑在相同频率范围下的结构模态振型和声学模态振型。所以,在选取前六阶声学振型声压的同时,再选取与结构模态前六阶频率相近的声学振型声压级,这样能更全面地分析两种模态的联系与规律。本文分别用x、y、z三个方向来表示横向、纵向和轴向来描述声学模态形状,以便于更加清晰准确观察声压、声压级的变化规律。
由图2可知,一阶模态是特征频率为509.79 Hz的轴向声模态,观察声压与声压级振型图可知,声压与声压级大小沿着轴向发生变化,而在纵向和横向这两个方向其声压与声压级大小基本保持不变。在壳体中间部分出现了一个纵向声压节面,节面两侧声压相位相反,声压与声压级的大小从壳体中间部分向两轴端逐渐增大。声压与声压级分别向壳体进气口、排气口端增大,且声压值最大的位置主要在壳体的轴端。
由图3可知,二阶模态是特征频率为648.32 Hz的纵向声模态,从声压与声压级振型图可以看出,声压与声压级的大小沿纵向变化,而在轴向与横向这两个方向声压与声压级的大小基本保持不变。在壳体的进气口、排气口的中间位置出现轴向节面,节面两侧声压相位相反。声压与声压级的大小沿着轴向节面向两端逐渐增大,且声压与声压级的最大值位置出现在进气口、排气端口处。
由图4可知,三阶模态是特征频率为681.93 Hz的横向声模态,由声压与声压级振型图可以看出,声压与声压级大小沿横向变化,而在纵向和轴向两个方向上声压与声压级的大小基本不变。在壳体声腔的横向轴端出现声压的轴向节面,节面两侧声压相位相反。声压与声压级的大小沿着节面沿着横向两侧幅值逐渐增大,且声压与声压级最大值的位置主要出现在声腔左右壁面两侧。
由图5可知,四阶模态是特征频率为908.27 Hz轴向与横向声模态,观察图中声压与声压级的分布可以看出,声压与声压级同时沿着轴向和横向两个方向发生变化,而在纵向声压与声压级变化不大。在壳体声腔体的两个轴端分别有一个横向节面,节面两侧声压相位相反,声压与声压级的大小分别沿节面两侧逐渐增大。从轴向来看,由于从横向进口处轴端到排气口处轴端声压与声压级变化方向正好相反。因此,声压与声压级在轴向分布上,进气口处的轴端与排气口处轴端也有两个声压与声压级变化方向,声压与声压级大小变化的方向也相反,且声压与声压级最大的地方出现在进气口侧的轴端。
由图6可知,五阶模态是特征频率为928.7 Hz的纵向和轴向声模态,观察图中声压与声压级的分布可以看出,声压与声压级同时沿着纵向和轴向两个方向发生变化,而在横向声压与声压级变化不大。在壳体声腔体的两个轴端分别有一个轴向节面,节面两侧声压相位相反,声压的大小分别沿节面两侧逐渐增大。从轴向来看,由于从纵向进口处轴端到排气口处轴端声压与声压级大小变化方向正好相反。因此,声压与声压级在轴向分布上,进气口处的轴端与排气口处轴端也有两个声压与声压级变化方向,声压与声压级大小变化的方向也相反,且声压与声压级最大值的地方出现在轴端。
由图7可知,六阶模态是特征频率为1033 Hz的轴向声模态,观察图中声压与声压级的分布可以看出,声压与声压级的大小主要沿着轴向发生变化,而在横向上声压与声压级变化不大。位于双螺杆空压机壳体内声腔位置前端进气口和后端排气口部分别有两个纵向节面,节面两侧声压相位相反,声压与声压级的大小沿着节面两侧逐渐增大。声压与声压级最大的位置是声腔壳体进气口轴端的位置。
从以上各阶模态可以看出,空压机壳体声腔表面在不同频率段声压及声压级分布,声学模态的振型主要表现为声压。而声压与声压级相互联系且声压级也是表现声学的一个参数,同时也模拟了声压级跟声压变化趋势,得出声压级与声压变化趋势基本一致。
3.2 声压及声压级整体分布规律
为了更加全面、整体地观察在一定特征频率范围内声压与声压级的变化规律,将特征频率范围内不同位置的声压与声压级结果绘制成图8。由图8(a)可以看出,在不同特征频率段下,声压在频率范围500~3000 Hz的特征频率下是波动状态,空压机壳体不同位置声压的大小不同,在同一特征频率下声压由大到小依次是进气口端、排气口端、轴端、壳体表面。再由图8(b)频率声压级图中,声压级在频率范围500~3000 Hz的特征频率下也是波动状态,还可以看出,在空压机壳体上不同的位置声压级大小也不同,在不同特征频率下,声压级在不同特征频率下也是波动状态,在同一特征频率下声压级由大到小依次是进气口端、排气口端、轴端、壳体表面。在空压机主要位置中,空压机壳体表面声压级是最大的,最小的是进口端。结合声压与声压级来看,声压级的波动跟声压波动趋势基本是一致的,在特征频率500~3000 Hz内,声压级的大小分布位置也与声压分布位置基本一致。

(a)不同频率下的声压分布规律 (b)不同频率下的声压级分布规律
4 结论
本文利用ANSYS与COMSOL对双螺杆空压机壳体进行结构模态与声学模态仿真分析,利用结构模态的频率范围得到了双螺杆空压机壳体的声学振型声压与声压级的云图。
(1)双螺杆空压机在工作时不仅要避免外部激励频率与系统固有频率相同产生结构共振,也还要避免产生声共振,从各阶次声模态分布来看,发生声共振时,空压机壳体不同位置所产生的声压与声压级的大小不同。因此,要避免在特征频率范围为500~3000 Hz内与声学特征频率相同产生声共振,应重点对发生声共振时声压与声压级高的地方进行结构优化与消音处理,避免激发出更大的噪声。
(2)在500~3000 Hz的特征频率范围内,不同特征频率的声压与声压级幅值大小不同,声压级变化趋势基本与声压一致,且都处于波动状态。在同一特征频率下,声压由大到小依次是进气口端、排气口端、轴端、壳体表面。由于壳体表面是噪声的表现载体,因此为了保证空压机正常工作且避免产生比较大的噪声,尽可能避免与声压大的地方频率相同。此分析结果可为后续空压机结构优化与降噪提供参考依据。
