复数学习中应关注的要点梳理
2022-03-14侯祥伟
侯祥伟
(山东省邹城市第二中学)
复数是历年各省市高考命题的必考点,但题目难度不大,属于学生不能失分的点,其命题视角主要涉及复数的基本概念、基本运算、复数的有关性质及复数的简单应用等.学生在学习中要准确把握复数的相关概念,熟练应用相应的运算法则、运算技巧等,小题不大做.下面总结几个要点,供读者参考.
1 掌握复数的基本概念
复数z=a+bi(a,b∈R,i为虚数单位,i2=-1),其中a为实部,b为虚部,复数是既有“大小”又有方向的量,其“大小”又称为复数的“模”,表示为|z|=;实部相等,虚部互为相反数的两个复数是共轭复数;当实部为0,虚部不为0时,z为纯虚数,当虚部为0时,z为实数.这些都是复数最基本的概念,以这些概念为视角的试题是高考常考题型.解题中要注意对概念进行辨析.
例1“a=0”是“复数z=a+bi(a,b∈R)为纯虚数”的( ).
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件

学生在解答本题时,常错选C.原因是忽视了复数z=a+bi为纯虚数的条件是a=0,且b≠0,故正确选项为B.
例2若复数z满足z+i=3-i,那么z的虚部是( ).
A.2 B.-2 C.2i D.-2i

学生在解答本题时,由于对复数有关概念的掌握不扎实,常错选A 或D.注意虚部是指i的系数,与其前面的符号是一个整体.故正确选项为B.
2 理解复数的几何意义
复数z=a+bi(a,b∈R)与复平面(实部为横轴,虚部为纵轴)内的点Z(a,b)一一对应.当z为实数时,该点落在横轴上,当z为纯虚数时,该点落在纵轴上(除原点).复数也可以与向量建立对应关系,即z=a+bi与向量对应,其中O为坐标原点.因此某些复数问题可借助向量运算来求解.
例3在复平面内,“点A在虚轴上”是“点A所对应的复数为纯虚数”的( ).
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件

学生在解答本题时易错选C,原因是忽视了特殊点,即坐标原点,它所对应的是实数0.故“点A在虚轴上”是“点A所对应的复数为纯虚数”的必要不充分条件.故正确选项为B.
例4已知复数z1,z2满足|z1|=1,|z2|=1,若z1+z2=1+,则|z1-z2|=_________.

3 熟练复数的运算
复数的运算包括加、减、乘、除以及相等.两个复数相加(减),将实部与实部、虚部与虚部分别相加(减).复数的乘法利用乘法分配律计算.复数的除法,利用两个共轭复数之积为实数的原理,将分母实数化来实现.两个复数相等,即实部与实部相等,虚部与虚部相等.其他相应的运算与实数的运算方法相同.注意in具有周期性,其最小正周期为4,即i4n=1,i4n+1=i,i4n+2=-1,i4n+3=-i;若ω=-,则ω0=1,ω2=,ω3=1;1+ω+ω2=0.另外要注意两个复数不能比较大小,但其模可以比较大小.
例5 若z=则|z|=( ).


本题考查了复数的除法运算及复数模的求解,属于基础题,只要准确计算即可.因为,所以z=,所以,故正确选项为B.
例6下列各选项中运算结果为纯虚数的是( ).
A.i(1+i) B.i2(1-i)
C.i(1+i)2D.(1+i)2

纯虚数,即实部为0,虚部不为0,只要利用复数的运算法则,逐一将各选项中的复数关系式进行计算化简即可.
选项A,i(1+i)=-1+i,不是纯虚数.
选项B,i2(1-i)=-1+i不是纯虚数.
选项C,i(1+i)2=-2不是纯虚数.
选项D,(1+i)2=2i为纯虚数.
综上,正确选项为D.
4 准确利用复数性质
共轭复数的性质:令z=a+bi(a,b∈R),其共轭复数为=a-bi,则z与在复平面内对应的点关于实轴对称.
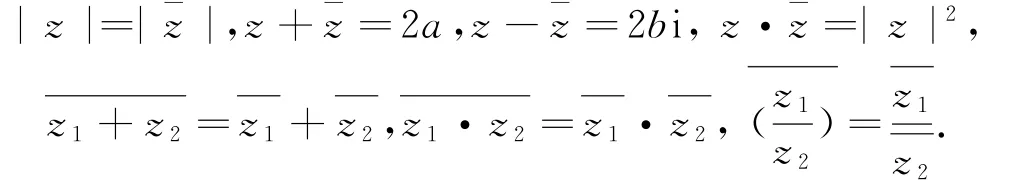
实数的共轭复数为其本身.
复数模的运算性质:‖z1|-|z2‖≤|z1±z2|≤|z1|+|z2|(复数模的三角不等式),|z1·z2|=|z1|·,|zn|=|z|n等,熟练利用这些性质,往往可以快速解题.
例7若复数z满足(1+i)z=2i,则|z|=( ).


根据题目所给关系式,可知z=,再结合复数模的性质,即,得

故正确选项为C.
例8现给出如下所述四个命题.p1:如果复数z满足∈R,那么z∈R;
p2:如果复数z满足z2∈R,那么z∈R;
p3:如果复数z1,z2满足z1z2∈R,那么z1=
p4:如果复数z∈R,那么∈R.
其中的真命题为( ).
A.p1,p3B.p1,p4
C.p2,p3D.p2,p4

假设z=a+bi(a,b∈R,且z≠0),那么R,据此可知b=0,故z∈R,即p1是真命题.
若z=i,而z2=i2=-1∈R,但z=i∉R,所以p2是假命题.
若z1=z2=i,则z1z2=-1∈R,而z1≠z2,所以p3是假命题.
实数的共轭复数即为其本身,亦为实数,所以p4是真命题.
综上,正确选项为B.
5 渗透复数数学文化
教育部考试中心在“关于普通高考考试大纲修订内容”中要求“增加中华优秀传统文化的考核内容,积极培育和践行社会主义核心价值观,充分发挥高考命题的育人功能和积极导向作用”.比如,在数学中增加数学文化的内容.将数学文化与数学知识相结合,加强引导学生对中华优秀传统文化的了解.因此近几年高考题、模拟题或竞赛题中出现大量以复数为载体的数学文化试题,有效地起到这一引导功能.
例9欧拉公式eiθ=cosθ+isinθ(e是自然对数的底数,i是虚数单位)是由瑞士著名数学家欧拉发现的,当θ=π时,就有eiπ+1=0,根据上述知识试判断表示的复数在复平面对应的点位于( ).
A.第一象限 B.第二象限
C.第三象限 D.第四象限

欧拉公式将三角函数的定义域扩大到复数,建立了三角函数和指数函数的关系,欧拉公式在复变函数里占有非常重要的地位.

例10在复平面内,复数z=a+bi(a,b∈R)与向量(O为坐标原点)对应,设=r.以射线Ox为始边,OZ为终边旋转的角为θ,则z=r(cosθ+isinθ).法国数学家棣莫弗发现了棣莫弗定理:z1=r1(cosθ1+isinθ1),z2=r2(cosθ2+isinθ2),则z1z2=r1r2[cos(θ1+θ2)+isin(θ1+θ2)],由此可导出复数乘方公式:[r(cosθ+isinθ)]n=rn(cosnθ+isinnθ).已知z=+i)4,则|z|=( ).

棣莫弗定理与例9中的欧拉公式有紧密的联系,如将复数改写为指数形式,即z1=r1eiθ1,z2=r2eiθ2,则z1z2=r1r2ei(θ1+θ2).

6 落实复数工具应用
复数既可以作为考点来考查,也可以作为工具用于解题,在处理某些函数最值问题或不等式证明问题时,通过构造复数,利用复数的运算及性质常可使问题简捷获解,主要的工具就是复数模的三角不等式:
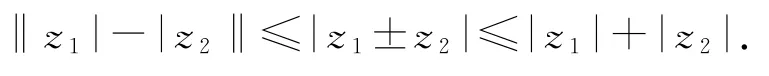
例11已知函数f(x)=(x∈R),则函数f(x)的最小值为________.

本题可以利用几何法求解,即“将军饮马”模型,也可以利用复数的性质简捷处理.
将函数变形得
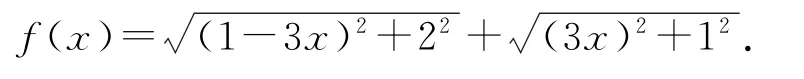
设复数z1=(1-3x)+2i,z2=3x+i,则|z1|=,利用复数模的三角不等式得|z1|+|z2|≥|z1+z2|=|1+3i|=,故函数f(x)的最小值为 10.
例12已知a,b,c∈R*,求证:
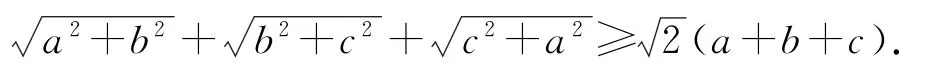

本题的证明方法很多,可以利用代数法,也可以利用几何法.在此利用复数法进行证明.
结合所证不等式的结构特征,设z1=a+bi,z2=b+ci,z3=c+ai,根据复数模的三角不等式得

综上,复数问题难度虽然不大,但要注意易错、易混问题的辨析,准确计算,避免造成无谓失分.上述几个要点,希望对学生的学习有所帮助.
(完)
