导数及其应用章节小测

侯有岐

(陕西省汉中市四〇五学校)

(本试卷共22小题,满分150分,考试用时120分钟)

一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的.)

1.使函数f(x)＝cosx在[0,]上取得最大值的x为( ).

2.对任意的x∈R,函数f(x)＝x3＋ax2＋7ax不存在极值点的充要条件是( ).

A.0≤a≤21 B.a＝0或7 C.a＜0或a＞21 D.a＝0或21

3.函数φ(x)的定义域为R,φ(－1)＝4,对任意的x∈R,φ′(x)＞6,则φ(x)＞6x＋2的解集为( ).

A.(－1,1) B.(－∞,－1) C.(－1,＋∞) D.(－∞,＋∞)

4.设函数f(x)＝lnx－ax2－bx,若x＝1是f(x)的极大值点,则a的取值范围为( ).

A.(－1,0) B.(－1,＋∞) C.(0,＋∞) D.(－∞,－1)∪(0,＋∞)

5.已知函数f(x)＝－－x2的最大值为f(a),则a＝( ).

6.若方程2x3－3x＋a＝0恰有两个解,则c＝( ).

7.设函数f(x)＝lnx－(m＞0)在定义域内不单调,则m－n的取值范围为( ).

A.(0,3) B.(3,＋∞) C.(－3,1) D.(－∞,3)

8.若y＝f(x)是奇函数,当x∈(0,6)时,f(x)＝lnx－ax(a＞),当x∈(－6,0)时,f(x)的最小值为1,则当x∈(－6,0)时,f(x)＝( ).

A.－ln(－x)－xB.ln(－x)＋xC.lnx－xD.－ln(－x)＋x

二、多选题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项是符合题目要求的.全部选对的得5分,有选错的得0分,部分选对的得2分.)

9.若函数y＝在(1,＋∞)上单调递减,则称f(x)为P函数.下列函数中为P函数的为( ).

11.已知直线l是曲线y＝ex与曲线y＝e2x－2的一条公切线,l与曲线y＝e2x－2切于点(a,b),且a是函数f(x)的零点,则f(x)的解析式可能为( ).

A.f(x)＝e2x(2x＋2ln2－1)－1 B.f(x)＝e2x(2x＋2ln2－1)－2

C.f(x)＝e4x(4x＋2ln2－1)－1 D.f(x)＝e2x＋1(2x＋2ln2－1)－2e

12.已知f(x)＝－lnx,f(x)在x＝x0处取得最大值,则( ).

三、填空题(本题共4小题,每小题5分,共20分.)

13.已知函数f(x)＝ex－ax在区间(0,1)上有极值,则实数a的取值范围是_________.

14.已知函数f(x)＝x3＋mx＋,g(x)＝－lnx.min{a,b}表示a,b中的最小值,若函数h(x)＝min{f(x),g(x)}(x＞0)恰有3个零点,则实数m的取值范围是________.

15.已知函数f(x)＝x3＋x2＋ax.若g(x)＝,对任意的x1∈,2],存在x2∈,2],使f′(x1)≤g(x2)成立,则实数a的取值范围是________.

16.曲线y＝lnx过原点的切线方程为_________,若点A在曲线y＝lnx上,且该曲线在点A处的切线经过点(－e,－1)(e为自然对数的底数),则点A的坐标是________.

四、解答题(本题共6小题,共70分.解答时应写出文字说明、证明过程或演算步骤.)

17.(10分)已知函数f(x)＝ax3＋bx＋c的图像经过点(0,1),且在x＝1处的切线方程是y＝x.

(1)求y＝f(x)的解析式;

(2)求y＝f(x)的单调递增区间.

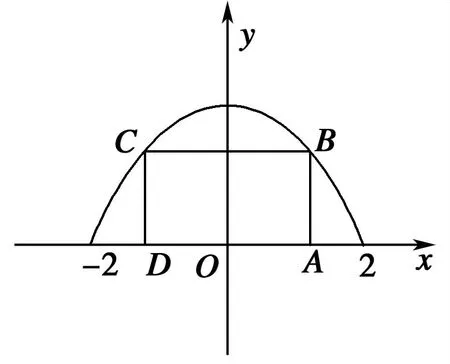
18.(12分)如右图所示,已知矩形的两个顶点位于x轴上,另外两个顶点位于抛物线y＝4－x2在x轴上方的曲线上,求矩形的面积最大时的边长.

19.(12分)设函数f(x)＝2lnx－x2＋ax＋2.

(1)当a＝3时,求f(x)的单调区间和极值;

(2)若直线y＝－x＋1是曲线y＝f(x)的切线,求a的值.

20.(12分)已知函数f(x)＝lnx＋(a∈R).

(2)当函数f(x)在x＝1处的切线平行于直线2x－y＝0时,若在[1,e]上存在一点x0,使得x0＋＜mf(x0)成立,求实数m的取值范围.

21.(12分)已知函数f(x)＝ax2－4alnx－14x.

(1)当a＝2时,求f(x)的最小值;

(2)讨论f(x)的单调性.

22.(12分)已知函数f(x)＝x2－(a＋1)x＋alnx＋1.

(1)若x＝2是f(x)的极值点,求f(x)的极大值;

(2)求实数a的范围,使得f(x)≥1恒成立.