基于第一性原理计算的ΙA族元素掺杂p型ZnO光电学特性研究*
2022-03-14肖原彬赵艳芳
肖原彬,赵艳芳
(江苏理工学院 机械工程学院,江苏 常州 213001)
0 引 言
氧化锌(ZnO)是一种最理想的宽带隙氧化物复合半导体,在LED发光二极管、紫外探测器、气体传感器、压电设备、太阳能电池透明导电氧化物层、压敏电阻和致发光(EL)器件中具有巨大的应用潜力[1-6]。ZnO具有在室温下禁带宽度Eg=3.37 eV,激子结合能高达60 meV,无毒,抗辐射和低生产成本,自然界储量丰富的性质[7]。ZnO近年来在发光二极管上的应用研究以异质结为主,然而异质结界面处往往存在较大的晶格失配,这导致了载流子浓度的降低,从而降低了发光二极管的发光效率,因此,制备ZnO同质结对于发光二极管的应用具有较大的价值。目前,对ZnO的n型掺杂改性已经较为成功,如Ⅲ族元素B[8],Al[9-10],Ga[11],In[12],然而p型转化却比较困难。Ⅴ族元素N[13]在受主掺杂中作为最适合的掺杂物,已经得到广泛的关注,但因其活性较差,与Zn难以成键,且N与N间排斥作用较强,导致掺杂的困难。为了克服N掺杂的这些缺点,常使用Ⅲ族和Ⅴ族元素共掺的方法[14-16]进一步提高N的固溶度。使用共掺的方法实验过程复杂,且制作难度较大,研究者们将目光投向ⅠA族元素,通过替代Zn原子来实现受主掺杂。
研究者们对Li[17]、Na[18]、K[19]掺杂ZnO进行了一些研究,发现ⅠA族元素的掺入实现了ZnO的p型转化。目前国内外学者对Li、Na、K掺杂ZnO在实验和理论方面进行了研究。如在实验研究方面,Xu等人[20]采用溶胶-凝胶法在不同的Si衬底温度上制备了1at.%的K掺ZnO薄膜,结果表明,所有样品均表现出强紫外发射和弱蓝光发射,其中,500℃退火后的样品晶体质量最好,紫外发射最强。Shinde等[21]研究了喷雾热解法制备的Li掺杂ZnO薄膜的光电及化学性能,发现在1%(原子分数)掺杂条件下制备的Li掺杂ZnO薄膜的电子迁移率最高,达到102 cm2/Vs,载流子浓度为3.62×1019cm-3。Zheng等[22]通过脉冲激光沉积的方法研究发现,随着ZnO中Na掺杂量的增加,导电类型从n型转变为p型。在理论研究方面, Hu 等[23]采用第一性原理研究了本征ZnO和Li-N、Li-2N 共掺ZnO的电子结构, 发现共掺对载流子浓度提高很大,而对光学性质影响不大。然而,从理论上对于ⅠA族元素掺杂形成的p型ZnO光电学性质进行比较的相关研究并不多。本文利用第一性原理研究了Li、Na、K掺杂ZnO的光电学性质,对实现ZnO的p型转化具有一定的意义。
1 模型及计算方法
常温常压下,理想ZnO晶体结构是空间群为P63mc的六方纤锌矿结构,ZnO原胞模型中包含两个Zn原子和两个O原子,实验晶格常数为a=b=0.325 nm,c=0.521 nm,键角α=β=90°,γ=120°。Zn-O键沿c轴方向的键长为0.1992 nm, 沿其他方向的键长为0.1973 nm。计算模型为包含32个原子的2×2×2超晶胞模型。掺杂时由于更易形成替位掺杂,因此一个Zn原子被一个Li(或Na、 K)原子取代,掺杂浓度为6.25%(原子分数),结构模型如图1所示。
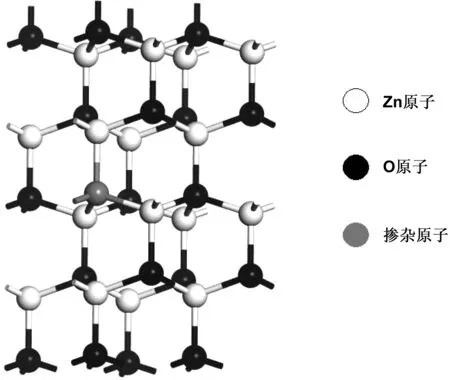
图1 ZnO掺杂体系的模型图Fig 1 Model diagram of ZnO doping system
计算采用了基于第一性原理的密度泛函理论平面波赝势法[24]。采用赝势用来代替价电子与内核电子间的作用,采用广义梯度近似(GGA)对电子间交换-关联势进行校正,选取Zn、O、Li、Na、K原子的价电子态分别为Zn-3d104s2、O-2s22p4、Li-2s1、Na-3s1、K-4s1。截断能设为400eV,布里渊区k点设为3×3×2,自洽收敛精度为5×10-6eV/原子。
2 结果与讨论
2.1 晶格结构和电学特性
为了获得稳定的结构,我们首先用第一性原理方法对ZnO超晶胞进行了几何优化。计算了本征ZnO、6.25%(原子分数)掺杂浓度的K掺ZnO、Li掺ZnO和Na掺ZnO的晶格常数,如表1所示,其超晶胞结构分别为ZnO、Zn0.9375K0.0625O、Zn0.9375Li0.0625O和Zn0.9375Na0.0625O。由表1可知,在掺杂Na和K的情况下,晶格常数(a,c)的计算值均略有增加,且c/a也有所增大,这可能是由于Na+和K+的离子半径(分别为0.102和0.138 nm)均大于Zn2+(0.074 nm)。当Na+和K+替代Zn2+时,晶格常数增大。在掺杂Li的情况下,晶格常数a略有降低,而晶格常数c略有增加,这可能是由于Li+(0.076 nm)的离子半径略大于Zn2+(0.074 nm)。当Li+取代Zn2+时,晶格常数a减小的原因可能是Li离子正电荷之间的斥力减小,使系统的能量减小。系统能量的减小导致晶胞体积和晶格常数的降低。同时Zn0.9375Li0.0625O的晶胞体积(0.19738 nm3),小于本征ZnO的晶胞体积(0.19918nm3)。

表1 本征 ZnO、Zn0.9375K0.0625O、Zn0.9375Li0.0625O和Zn0.9375Na0.0625O的晶格常数Table 1 Lattice constants of pureZnO, Zn0.9375K0.0625O, Zn0.9375Li0.0625O and Zn0.9375Na0.0625O
图2为本征ZnO的能带结构。0 eV中的短点线为费米能级,从图2可以看出,导带底(CBM)和价带顶(VBM)在同一个k点(G)处,说明ZnO是一种直接带隙半导体。本征ZnO的带隙为0.73 eV,与Xie等[25]计算出的0.74 eV和Osuch等[26]用第一性原理方法计算出的结果0.75 eV基本一致,但明显低于实验值(3.37 eV)。这主要是因为GGA高估了ZnO中Zn3d态电子的能量,导致ZnO与O2p态相互作用增大,带隙缩小。虽然计算值低于实验值,但并不影响G点附近能带结构的电子结构理论分析。
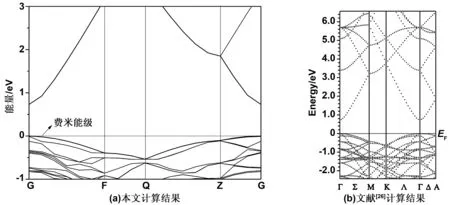
图2 本征ZnO的能带结构Fig 2 Band structure of pure ZnO
本征ZnO能带中价带由三部分组成:上价带部分(-3.8~0 eV)、下价带部分(-6.7~-3.8 eV)和能级很深部分(-18.6~-16.0 eV)。-18.6~-16.0 eV区域与导带之间相互作用很弱,对导电性影响几乎很小,影响半导体导电性质的主要是费米能级附近的上价带部分,因此,掺杂结构主要在这个范围内讨论能带结构的变化。
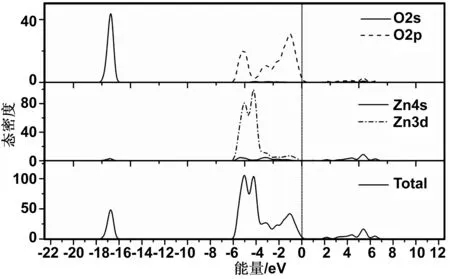
图3 本征ZnO的态密度Fig 3 Density of states of pure ZnO
图3为本征ZnO的总态密度(PDOS)和分波态密度(TDOS)图,结合图2分析可知:能带的上价带部分主要由O2p态电子组成;下价带主要由Zn3d态电子组成;-18.6~-16.0 eV的部分由O2s状态贡献。Zn4s态电子有明显的向O2p态移动的趋势,表明ZnO是一种强离子键而弱共价键的半导体材料。其中,CBM主要由Zn4s态电子控制,VBM主要由O2p态电子控制。
图4(a)~(c)分别为Zn0.9375K0.0625O、Zn0.9375Li0.0625O和Zn0.9375Na0.0625O近费米能级处的能带结构。可以看出,K掺杂ZnO的费米能级在价带之上,说明K掺杂并未改变ZnO的导电类型;Li、Na掺杂的ZnO费米能级都进入了价带,形成了p型导电半导体。Li掺ZnO和Na掺ZnO在价带之上都形成了两条浅的受主杂质能级。
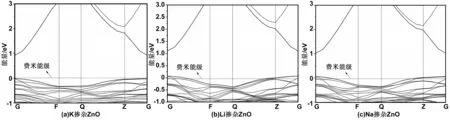
图4 掺杂ZnO的能带结构Fig 4 Band structrues of doped ZnO
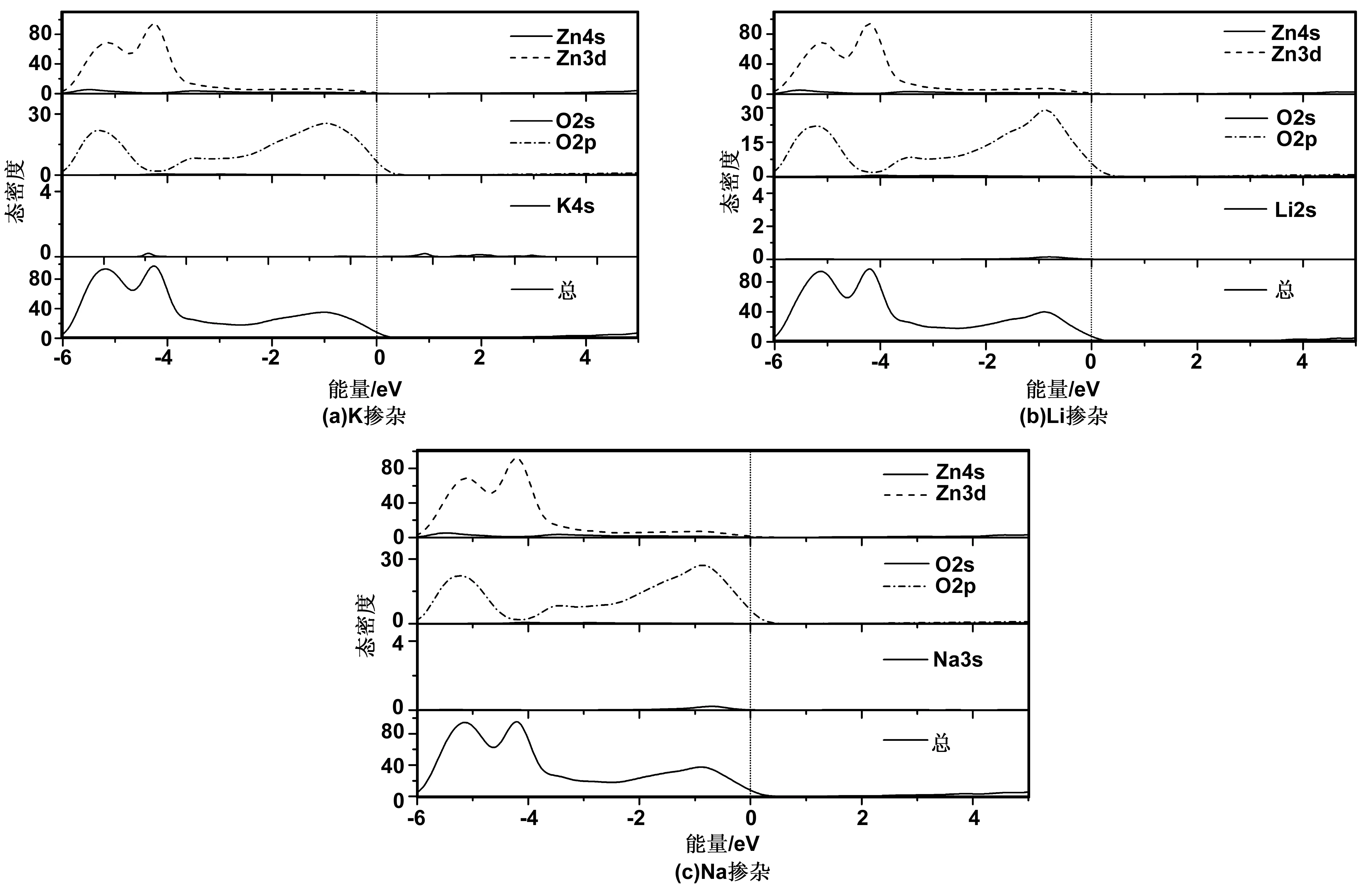
图5 掺杂ZnO近费米能级处态密度Fig 5 DOS near Fermi level of doped ZnO
为了更精确分析各掺杂对ZnO导电性的贡献,进一步分析了其态密度结构。图5(a)~(c)分别为Zn0.9375K0.0625O、Zn0.9375Li0.0625O和Zn0.9375Na0.0625O近费米能级处的总态密度和各分波态密度图。可以看出,K掺杂ZnO价带顶处导电主要由O2p态电子贡献,K4s几乎没有作用;Li掺ZnO价带顶处导电主要由O2p和Li2s态电子控制;Na掺ZnO价带顶处导电主要由O2p和Na3s态电子控制。说明Li2s和Na3s态电子分别对Li掺ZnO和Na掺ZnO形成的p型半导体有一定的贡献。
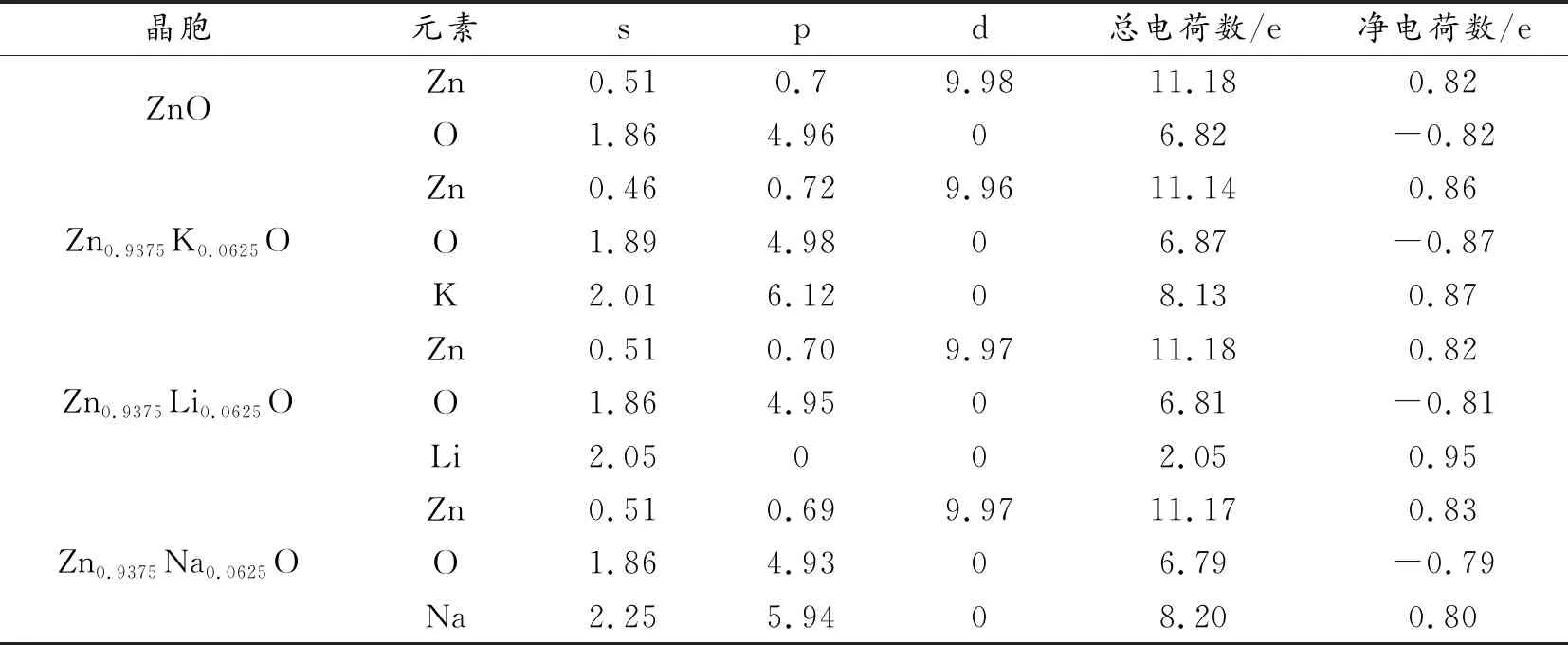
表2 本征ZnO及不同掺杂ZnO体系下的电荷分布Table 2 Charge distribution of pureZnO and different doped ZnO situation
表2是本征ZnO及不同掺杂条件下的电荷分布,可以看出,本征ZnO中,Zn原子价电子主要分布在d轨道上,失去0.82个价电子,同时O原子价电子主要分布在p轨道上,得到0.82个价电子,本征ZnO表现出不导电的特点;Zn0.9375K0.0625O中Zn原子失去了0.86个价电子,同时O原子得到了0.87个价电子,高于本征ZnO的0.82个,K原子价电子平均有0.87个发生转移,在Zn0.9375Li0.0625O掺杂体系中Li原子价电子平均有0.95个发生转移,在Zn0.9375Na0.0625O掺杂体系中Na原子价电子平均有0.80个发生转移,掺杂元素失去价电子数越多,越有利于向p型导电的转变,可以看出,Zn0.9375Li0.0625O掺杂体系中失去的价电子最多,因此Zn0.9375Li0.0625O具有相对较好的p型导电性。
2.2 光学性质
在ε1=n2-k2,ε2= 2nk的线性响应范围内,介质的光学性质可用ε(E)=ε1(E)+iε2(E)的复介电响应函数来描述。众所周知,虚部ε2(E)是对任何材料光学性质的概述。用Kramers-Kronig色散关系可以计算虚部ε2(E)和实部ε1(E)。同时,吸收系数α(E)、反射系数R(E)等光学参数可以通过ε2(E)和ε1(E)计算得到,计算公式如下:
(1)
(2)
其中,λ是真空中波长。
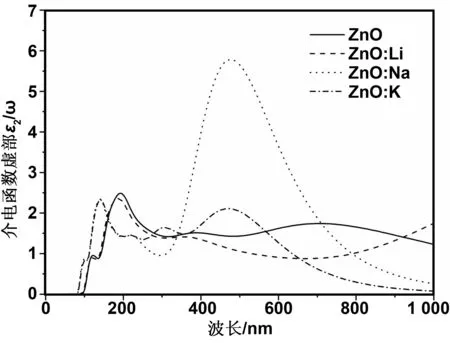
图6 本征ZnO和不同掺杂情况的介电函数虚部Fig 6 Dielectric function imaginary parts of pure ZnO and different doping conditions
图6为不同掺杂情况的介电函数虚部。介电函数虚部决定材料的吸收光谱性质。从图6可以看出,在本征ZnO中,第一个阈值在84 nm左右,当波长大于84 nm时,虚部值迅速增加,相应光谱中的峰来源于价带与导带之间的电子跃迁。本征ZnO介电函数虚部图中出现3个主要的峰,分别位于122、193和704 nm处。其中,122 nm处的峰来自于下价带Zn3d态到导带O2p态的光学跃迁,193 nm附近的第二个峰是由下价带Zn3d态到O2s态的光学跃迁,704 nm附近的峰主要来自于上价带O2p态到Zn4s态的光学跃迁。掺入Li、 Na、 K后,介电函数虚部3个峰都向高能方向移动(蓝移),认为蓝移是由Li、Na、K的掺入引起的,其中Li掺杂ZnO蓝移较少。Li、Na、K掺杂后,在122和193 nm处峰强变化不大,而在704 nm处的峰强出现了明显的变化,Li掺ZnO结构在704nm处几乎没有峰,K掺ZnO峰蓝移至471 nm处,峰强有一定的增强,Na掺ZnO结构与本征ZnO相比,第3个峰蓝移至480 nm处,峰强增大了3倍左右。
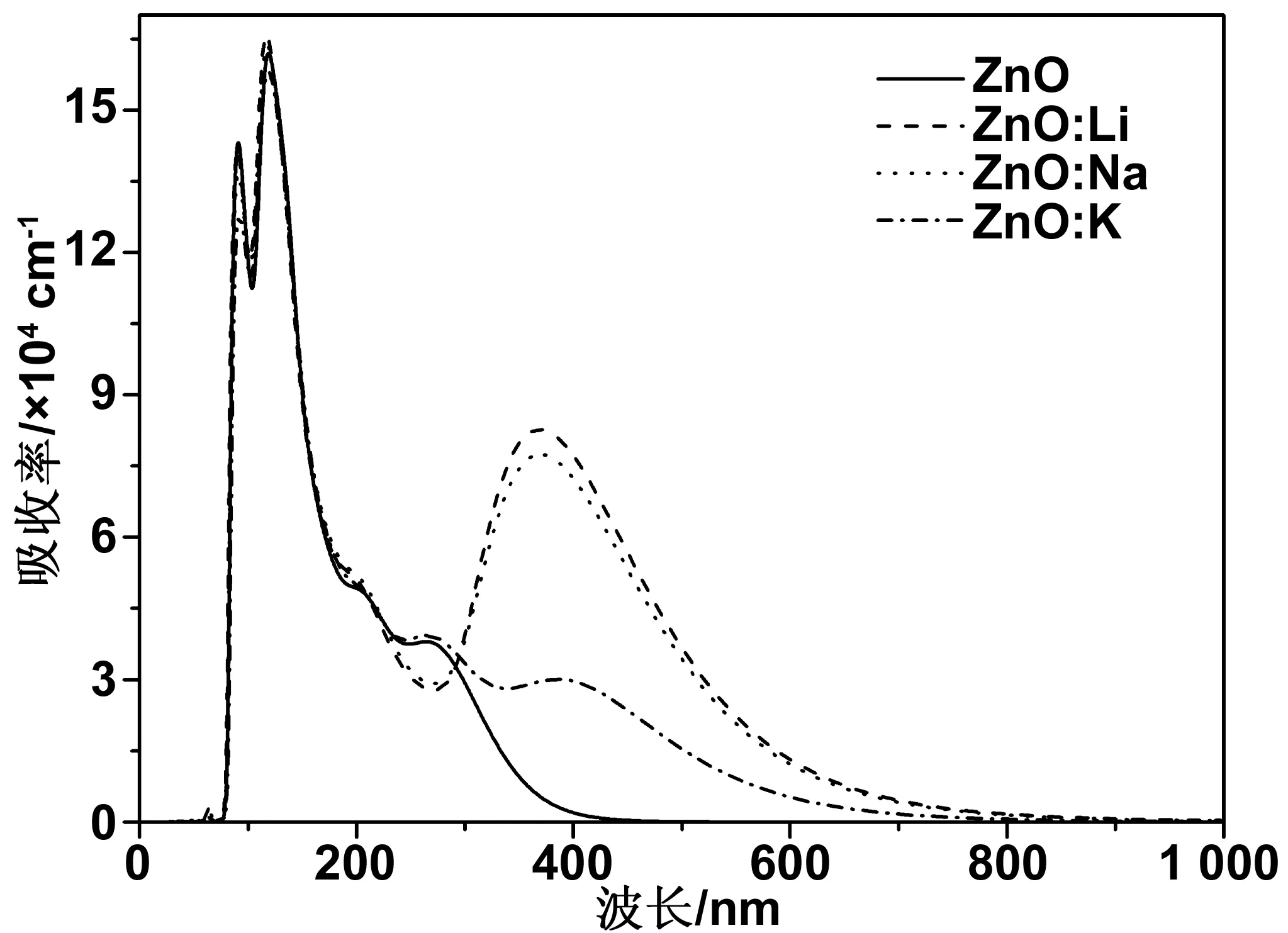
图7 本征ZnO和不同掺杂情形下的吸收系数曲线Fig 7 Absorption coefficient curves of pure ZnO and different doping conditions
图7为本征ZnO和不同掺杂情形下的吸收系数曲线。从图中可以看出,在100~200 nm的真空紫外光区,各掺杂ZnO与本征ZnO相比变化很小,几乎可以忽略。本征ZnO在可见光区吸收率几乎为零,说明本征ZnO只对紫外光有吸收,对可见光几乎零吸收。Li、 Na、 K掺杂ZnO后,可以观察到在可见光区出现了明显的吸收,其中在可见光区的峰值出现在380 nm附近,Li掺ZnO峰值较强,Na掺ZnO次之,K掺ZnO的峰值较弱。
3 结 论
采用基于DFT的第一性原理研究了本征ZnO和Li、Na、K掺杂ZnO的晶格结构、电子结构和光学性质。在ZnO掺杂Na或K的情况下,晶格常数(a,c)的计算值均略有增加,在掺杂Li的情况下,晶格常数a略有降低,而晶格常数c略有增加,同时Zn0.9375Li0.0625O的晶胞体积(0.19738 nm3)小于本征ZnO的晶胞体积(0.19918 nm3)。从能带结构和态密度图可以看出,K掺杂并未改变ZnO的导电类型,Li、Na掺杂的ZnO费米能级都进入了价带,形成了p型导电半导体;Li2s和Na3s态电子分别对Li掺ZnO和Na掺ZnO形成的p型半导体有一定的贡献。从电荷分布可以看出,Li掺ZnO具有相对较好的p型导电性。Li、Na、K掺杂ZnO后,可以观察到吸收率在可见光区出现了明显的增大,其中Li掺ZnO在380nm附近峰值较强,这对ZnO在LED发光二极管上的应用具有一定的参考价值。
