非线性特征值问题平移幂法的不动点分析

唐耀宗 杨庆之

(1.喀什大学 数学与统计学院,新疆喀什 844000;2.南开大学 数学科学学院,天津 300071)

§1 引言

玻色-爱因斯坦凝聚态(简称BEC)的基态,即能量最低时的状态,目前是量子力学领域中一个重要而且活跃的研究课题[1-4],其离散情形可以描述为球面约束下的非凸最小化问题[5]

其中A ∈Rn×n×n×n是4 阶对称张量,B∈Rn×n是对称半正定矩阵,x∈Rn是向量.

对上述优化问题的Lagrange函数求梯度,容易验证其Karush-Kuhn-Tucker(KKT)系统即为非线性特征值问题

BEC基态解对BEC问题的理论研究以及实验指导具有重要意义.对于基态解的存在和唯一性探讨,可以参考[6-7]和其中的参考文献.作为NP难的BEC基态问题[8],通常采取两类数值方法进行求解.第一类是在球面约束条件下,利用非线性特征值格式(2) 设计不同类型的数值方法[9-15].第二类是求解球面约束下的极小化优化问题格式的方法[8,16-23].文献[5]中对更一般的NP难的BEC类非线性特征值问题采用了平移对称高阶幂法(SS-HOPM)进行求解,体现了较好的数值计算效率,并且能够保证点列收敛性[24].

本文将在文献[5,24]的基础上进一步对SS-HOPM算法进行不动点分析,以从理论上说明使用平移对称高阶幂法可以求得的非线性特征对类型.

本文的结构如下:§2介绍了相关的基础知识和基本术语.§3简单介绍了BEC类非线性特征值问题的SS-HOPM算法及其不动点分析.§4对本文进行了简单总结.

§2 基本概念和术语

在本文中,用Σ表示Rn上的单位球面,即

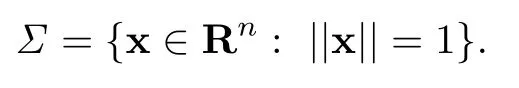
2.1 张量相关概念

本文采用文献[25]中的张量,矩阵以及向量的表示方法.即向量用黑体小写字母表示,如a.矩阵用黑体大写字母表示,如A.张量由Euler手写体表示,如A.标量用小写字母表示,如a.

对称张量在指标任意排列下其元素都是不变的.下面给出对称张量及相关概念的定义.

定义2.1[26]如果张量A ∈对所有i1···im ∈{1,···,n}以及p ∈Πm,均有

成立,则称张量A是对称的,其中Πm表示了(1,···,m)所有置换的集合.

定义2.2[26]设A ∈是对称张量,且x∈Rn.那么张量A与向量x的m −r次乘积可以表示为

其具体表达式为

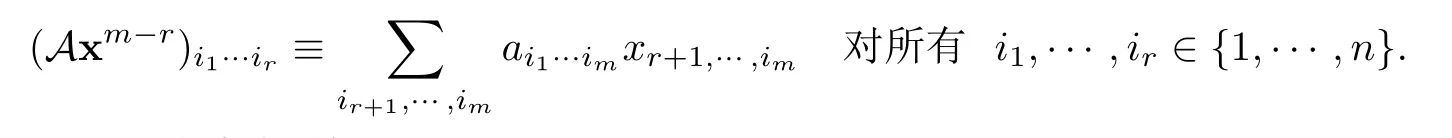
2.2 不动点相关知识

本文将要用到不动点的相关概念和性质,罗列如下.

定义2.3[27]假设φ:Rn →Rn,如果存在δ >0,对由任何满足‖x0−x∗‖ ≤δ的x0和由xk+1=φ(xk)所定义的序列{xk}都收敛到x∗,则称x∗是φ的吸引不动点.

定理2.1[28]设x∗为φ:Rn →Rn的不动点,J:Rn →Rn×n为φ的Jacobian矩阵.如果σ=ρ(J(x∗))<1,那么x∗为φ的吸引不动点；如果σ >0,那么迭代xk+1=φ(xk)以线性速率σ收敛.

定理2.2[29]设x∗为φ:Rn →Rn的不动点,J:Rn →Rn×n为φ的Jacobian矩阵.如果σ=ρ(J(x∗))>1,那么x∗为φ的不稳定不动点.

§3 非线性特征值问题的SS-HOPM算法及不动点分析

3.1 非线性特征值问题的SS-HOPM算法

在文献[10]中,作者构建了非齐次约束优化问题

的稳定点与BEC类非线性特征值问题

的特征对之间的联系,然后将由Kolda和Mayor[30]提出的用于齐次优化问题求解的SS-HOPM算法推广到了上述的非齐次约束优化问题,以求解BEC类非线性特征值问题.

从文献[24]可知,对于凸的情形,平移项α >0必须要大于某个参数β才能确保SS-HOPM算法收敛,其中β定义如下

SS-HOPM算法如算法1所述.

3.2 SS-HOPM算法的不动点分析

对于约束优化问题而言,Lagrange投影Hessian阵在决定不动点是否为局部极值方面起着关键作用.从文献[5]可知

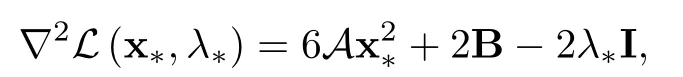
根据约束优化问题的Lagrange函数的Hessian阵与x∗正交的子空间的关系,可以把Lagrange投影Hessian阵定义为

其中U∗∈Rn×(n−1)的列形成了的正交基.根据C(λ∗,x∗)的谱性质可以对BEC类非线性特征值问题(2)的特征对进行分类.

定义3.1设A ∈Rn×n×n×n为对称张量,B∈Rn×n为半正定矩阵,(λ,x)是BEC类非线性特征值问题(2)的特征对.如果C(λ,x)是正定的,则特征对(λ,x)是正稳定的；如果C(λ,x)是负定的,则特征对(λ,x)是负稳定的,如果C(λ,x)是不定的,则特征对(λ,x)是不稳定的.

下面采用不动点理论对SS-HOPM算法进行分析,以区分哪种类型的特征对可以使用SSHOPM算法求得.即首先通过Langrage投影Hessian阵来判断特征对是正稳定的,负稳定的还是不稳定的;然后依据不同情形下特征对进行对照即可.

不失一般性,考虑凸的情形下的SS-HOPM算法视为不动点迭代

其中φ定义为

那么

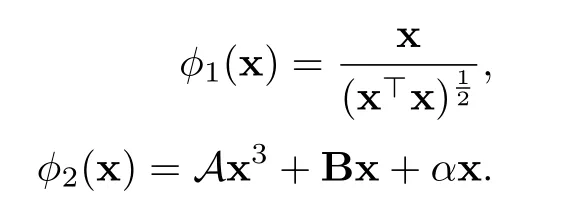
注意特征对(λ,x)当且仅当λ+α>0时是一个不动点,这对于α>β始终是正确的[24].

算子φ的Jacobian矩阵可以从下面的公式导出,即

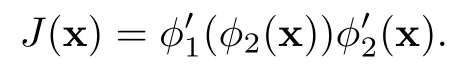
容易得到

在任何特征对(λ,x)处,都有

因此x处的Jacobian矩阵为

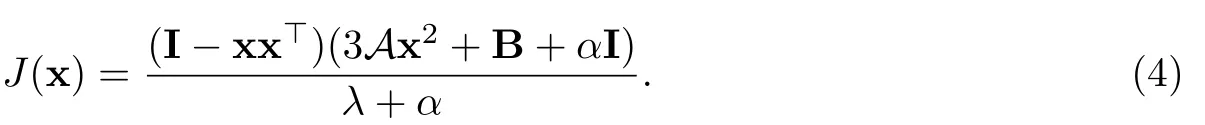
由Ax2,B和xx的对称性,容易验证Jacobian矩阵J(x)是对称的.

定理3.1设(λ,x)为非线性特征值问题(2)的特征对.假设α ∈R满足α >β,其中β ≡maxx∈Σ ρ(3Ax2+B).设φ(x)由(3)给定.那么当且仅当x是φ的线性吸引不动点时,(λ,x)是负稳定的.

证假设(λ,x)是负稳定的,算子φ在x处的Jacobian矩阵的形式如(4)所示.根据不动点理论,要证明x是算子φ的线性吸引不动点,只需要验证ρ(J(x))<1.

因为Jacobian矩阵J(x)是对称的,所以对于所有的y∈Σ,ρ(J(x))=|yJ(x)y|.还需要进一步证明,对于所有y∈Σ,|yJ(x)y|<1.因为J(x)x=0,因此限制y∈x⊥,故而y∈Σ∩x⊥,

那么

因为(λ,x)负稳定即意味着C(λ,x)是负定的；因此要|yJ(x)y| <1,则必须y(3Ax2+B)y<λ.根据β的定义,可以知道β ≥ρ(3Ax2+B).由λ+α>0可得

即ρ(J(x))<1,所以x是φ的线性吸引不动点.

另一方面,如果(λ,x)不是负稳定的,那么存在w∈Σ使得w∈x⊥,而且w(3Ax2+B)w≥λ.那么

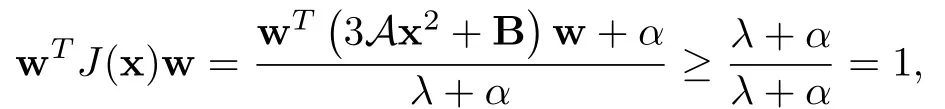
即ρ(J(x))≥1,根据不动点理论可知,x不是算子φ的线性吸引不动点.

实际上从上面的证明可以推断出,如果特征对(λ,x)不是负稳定的,则不存在α ∈R使得ρ(J(x))<1成立.换言之,如果(λ,x) 不是负稳定的,由于x是一个不动点,必有λ+α>0,进而ρ(J(x))≥1,那么较小的α当然不会出现“意外”的特征对收敛情形.

换句话说,如果α >β,那么任何球面Σ上的吸引不动点都必然是f(x) 的严格约束局部极小值.因为从定理3.1可知,只要α >β,目标函数的凸性即可满足.球面Σ上x任何收敛邻域中的点˜x必然满足f(˜x)>f(x),由此表明x为严格局部极小值.反之,如果α >β,任何严格局部极小值必然对应于某个吸引不动点.

定理3.1在凹的情况下的类似定理表述如下.

定理3.2设(λ,x)为非线性特征值问题(2)的特征对.假设α ∈R,满足α <−β,其中β定义为β ≡maxx∈Σ ρ(3Ax2+B).设φ(x)由(3)给定,那么当且仅当x是−φ的线性吸引不动点时,(λ,x)是正稳定的.

由矩阵幂法产生的序列{xk}总是收敛到谱特征值λ1对应的特征向量,其他特征向量均可能不是稳定不动点.与矩阵幂法相比,采用平移对称高阶幂法求解非线性特征值问题,可以找到多个特征对,因为可能存在多个正,负稳定特征对.但找到多个特征对的能力也意味着不能保证从任意初始点开始的迭代收敛到某个特定的特征对.

§3 结束语

SS-HOPM算法在求解中小规模的BEC类非线性特征值问题时具有不错的计算效率,同时还满足点列收敛性.本文进一步采用不动点分析,从理论上区分了采用平移对称高阶幂法所能求得的非线性特征对类型.

平移对称高阶幂法之所以能够保证收敛,在于其通过平移项的作用能够保证目标函数在整个迭代过程中保持凸性或凹性.不过其中平移项的选择却是一个不小的挑战.因为只有合适的平移项才能既保证收敛,又能保证好的收敛速率.设想在每次迭代中都重新设定一个平移项,使得每次迭代过程中的目标函数凸,从而既保证收敛,又不降低效率.我们将在以后的工作中将平移项的自适应改进作为进一步研究的课题.