6元素集合上T0拓扑总数的计算
2022-03-14曾佳泓
曾佳泓,赵 浩
(华南师范大学 数学科学学院,广东广州 510631)
§1 引言
布尔巴基学派学者以结构主义观点从事数学分析,他们认为数学包含三大结构:序结构,拓扑结构和代数结构,称为母结构.由母结构的相互交叉可以派生,演变出更多的数学结构.20世纪60年代,Dana Scott为λ演算找寻指称语义而提出Domain理论[1-2].
作为研究域的特定种类偏序集合的数学分支,Domain理论亦被看作序理论的分支,在计算机科学和数学领域中广泛应用.Domain理论体现了序与拓扑的相互结合,相互作用.其中一个重要的结论是:一个偏序集是连续的当且仅当其上的Scott拓扑是完全分配格[3-4].因此,可以利用内蕴拓扑研究偏序结构,亦可以利用偏序结构研究相关的拓扑结构.[3-5]
拓扑学致力于研究几何图形或空间在连续改变形状后还能保持一些不变的性质.拓扑学中一个基本问题是:n元素集上拓扑总数的计算.在现有研究中,大部分学者利用计算机编程以穷举运算求解拓扑总数.若不借助计算机求解,亦可考虑有限集上T0拓扑总数和非T0拓扑总数,但其中T0拓扑总数的计算难度较大.
文献[6-7]从Domain理论在拓扑领域的应用出发,利用序与拓扑的交叉,得到n=1,2,3,4,5时的T0拓扑总数分别为1,3,19,219和4231,相应的拓扑总数为1,4,29,355和6942.本文在其研究的基础上利用序与拓扑交叉的方法,结合Hasse图和层级配比数辅助分类,进一步给出6元素集合上的T0拓扑总数的计算,得到本文主要结论.
定理1.1设X为6元素集合,则X上的T0拓扑个数为130023.
§2 相关概念及引理
首先介绍本文涉及的相关定义,它们大多采自于文献[6-8].
定义2.1[8]设X为集合,记≤是X上的二元关系.若≤满足:(1)x ∈X,x ≤x;(2) 对任意x,y,z ∈X,x ≤y,y ≤z ⇒x ≤z;则称≤是X上的预序,称(X,≤)为一个预序集.
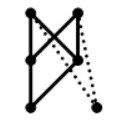
定义2.2[8]设X为集合,若≤满足:对任意x,y ∈X,x ≤y,y ≤x ⇒x=y;则称≤是X上的偏序,称(X,≤)为一个偏序集.其中,用x 定义2.3[6-7]设X为预序集,称m ∈X为一个极小元,如果对任意x ∈X,x ≤m ⇒m ≤x. 定义2.4[6-7]设X为预序集,称其非空子集D为定向集,若对任意x,y ∈D,存在z ∈d,使x ≤z,y ≤z. 定义2.5[6-7]若A ⊆X,记↑A={y ∈X:∃x ∈A,x ≤y}及↓A={y ∈X:∃x ∈A,y ≤x}.将↑{y}及↓{y}简记为↑y和↓y. 定义2.6设X为预序集,A ⊆X.A称为X的Scott-闭集[1,9],如果满足:(1)↓A=A;(2) 对任意定向集D ⊆X,若存在D的上确界supD,则有supD ∈A. 记X上的全体Scott-闭集为σ∗(X).X上Scott-闭集的补集全体形成X上的拓扑,称为Scott拓扑,记作σ(X). 定义2.7[1,9]设X为拓扑空间.X上的特殊化序≤定义为:x ≤y当且仅当x ∈{y}−,其中{y}−为独立点{y}的闭包. 本文所用计算理论基于以下的命题和引理,大多采自于文献[1-2]. 命题2.1[6-7]预序集X的序和其上的Scott拓扑的特殊化序是一致的.若X为T0拓扑空间,则X上的特殊化序为偏序.若X为非T0拓扑空间,则X上的特殊化序为预序,这样的预序称为真预序. 引理2.1[6-7]设X为有限集,τ和η为其上的两个拓扑,则τ=η当且仅当其诱导的特殊化序相等.对于X上的两个预序≤1及≤2,则两个预序相同当且仅当其诱导的Scott拓扑相同. 以上引理说明,有限集上的拓扑与其上的预序形成一一对应,且T0拓扑对应于偏序,非T0拓扑对应于真预序. 引理2.2[6-7](Zorn引理) 对任意的非空偏序集,若任意全序子集都有上界,则该偏序集必然存在极大元.对偶地,对任意的非空偏序集,若任意全序子集都有下界,该偏序集必然存在极小元. 引理2.3[6-7]设X为有限偏序集,记其极小元集合为min(X).若x ∈Xmin(X),则存在x0∈X,使得x0≤x. 引理2.4[6-7]设X为有限偏序集,对任意y ∈X,↓y∩min(X)/=∅. 定理2.5[6-7]设X为有限偏序集,若x ∈Xmin(X),则存在m0∈min(X),使得m0≤x. 随着集合中元素个数的增加,层级分类趋于复杂,因此用每个层级所含的元素个数按序组成一个n位数序列,称之为层级配比数.例如,当6元素集分为3个极大元,1 个中间元和2个极小元时,层级配比数记为000312. 引理3.1当有限集X含有6个极小元时,可形成1个偏序. 证这时为离散偏序,其层级配比数为000006,共1个. 引理3.2当有限集X含有5个极小元时,可形成186个偏序. 证剩下的元至少大于1个极小元,其层级配比数为000015.此时共有偏序数为 引理3.3当有限集X含有4个极小元时,可形成5325个偏序. 证对剩下的2个元分以下情况. 情形1若剩下的2个元不可相互比较,则其与极小元形成的偏序数均为=15.如图3.3.1,层级配比数为000024. 图3.3.1 此时共有偏序数为 人才梯队是根据企业的增长来匹配的,只能提前一点点,不能提前很多,提前很多会造成浪费。但一定要有梯队,因为没有梯队,后面的机制是会失灵的。没有梯队,机制会失灵;没有评价,机制会死机;没有选择,组织会板结。这三点非常重要。 情形2若剩下的2个元可以相互比较,则较小元至少大于一个极小元.如图3.3.2,层级配比数为000114. 图3.3.2 故此时共有偏序数为 因此,当有限集X含有4个极小元时,一共可形成3375+1950=5325个偏序. 引理3.4当有限集X含有3个极小元时,可形成35660个偏序. 证对剩下的3个元,按极大元的个数分以下情形. 情形1含有3个极大元,层级配比数为000033,即剩下的3个元不可相互比较.则每个元与极小元形成的偏序数均为=7.此时共有偏序数为 情形2含有2个极大元,层级配比数为000213.根据第3元与2个极大元的关系分以下情况. 图3.4.1 (1) 第3元小于2个极大元,且至少大于1个极小元. 而对可与第三元比较的极大元分以下情况. 情形3含有1个极大元,根据另外的2个元的关系分以下情况. (1) 若该2个元不可比较,称为较小元,层级配比数为000123,如图3.4.2.则该2个元分别与极小元形成=7种选择.值得注意的是以下两种特殊情况: 图3.4.2 ①当该2个元只大于同一个极小元时,极大元可大于另外的1或2个极小元. ②当该2个元一共大于2个极小元时(2个元各大于1个极小元(不相等) ;其中1个元大于2个极小元,1个元大于其中1个极小元;每个中间元都大于2个极小元;),极大元可大于剩余的1个极小元. 此时共有偏序数为 (2) 若2个元可比较,层级配比数为001113,如图3.4.3.即除极小元外的3个元可相互比较,则首先有=6种选择.将该3个元分别称为“大元”,“中元”,“小元”. 图3.4.3 对小元与极小元的关系分以下情况. ①当小元大于1个极小元时,有以下情况. 此时共有偏序数为 因此,当有限集X含有3个极小元时,一共可形成35660个偏序. 引理3.5当有限集X含有2个极小元时,可形成63465个偏序. 证对剩下的4个元,按极大元的个数分以下情形. 情形1含有4个极大元,层级配比数为000042.即剩下的4个元相互不可比较.则每个元与极小元形成的偏序数均为=3.此时共有偏序数为 情形2含有3个极大元,层级配比数为000312,如图3.5.1.根据第4元与极大元的关系分以下情况. 图3.5.1 (1) 第4元小于3个极大元,且至少大于1个极小元. 情形3含有2个极大元.称极大元和极小元以外的2个元为“中间元”.根据2个中间元的关系分以下情况.(1) 2个中间元不可相互比较,层级配比数为000222,如图3.5.2.根据极大元和中间元的关系分以下情况. 图3.5.2 图3.5.3 此时共有偏序数为 ④当2个极大元均大于2个中间元时,2个中间元与极小元均形成=3种选择.值得注意,当2个中间元只大于同一个极小元时,2个极大元均可单独大于另外的极小元. 图3.5.4 此时共有偏序数为 (2) 若2个中间元可比较,层级配比数为002112,则首先有=2种选择.称其中较大(小) 者为“较大(小) 元”.根据中间元与极大元的关系分以下情况. 图3.5.5 ②当1个极大元大于较大元,而另一个极大元只大于较小元时,有以下情形:若较小元大于1个极小元,则只大于较小元的极大元可单独大于另外的极小元,并且另一极大元和较大元有至多1个可同时大于该极小元;若较小元大于2个极小元,则有=1种选择. 此时共有偏序数为 此时共有偏序数为 情形4含有1个极大元.称极大元和极小元以外的3个元为“中间元”.根据3个中间元的关系分以下情况. (1) 若3个中间元不可相互比较,层级配比数为000132,如图3.5.6.每个中间元与极小元均形成=3种选择.值得注意的是,当3个中间元只大于1个极小元时,极大元可单独大于另外的极小元. 图3.5.6 此时共有偏序数为 (2) 若有2个中间元不可相互比较,且同时大于第3个中间元,层级配比数为001212,如图3.5.7.则首先有=3种选择.此时较小中间元与极小元形成=3种选择.需要注意,当较小中间元大于1个极小元时,至多1个极大元或2 个较大中间元可大于另外的极小元. 图3.5.7 此时共有偏序数为 图3.5.8 此时共有偏序数为 (4) 若有1个中间元大于另外2个中间元且该2个中间元不可比较,则2个较小的中间元均与极小元形成=3种选择.层级配比数为001122,如图3.5.9.值得注意的是,当较小中间元大于同一个极小元时,较大中间元和极大元至多有1个可以单独大于另外的极小元. 图3.5.9 此时共有偏序数为 图3.5.10 ①当小元大于1个极小元时,极大元,大元和中元至多有1个可以单独大于另外的极小元,有=8种选择; 此时共有偏序数为 因此,当有限集X含有2个极小元时,一共可形成63465个偏序. 引理3.6当有限集X含有1个极小元时,可形成25386个偏序. 证该极小元也是最小元.其余5个元形成的5元偏序数为P5=4231,则此时共有偏序数为 因此,当有限集X含有1个极小元时,一共可形成25386个偏序. 本节将利用§3的结论来证明本文的主要定理. 定理1.1的证明由引理3.1-3.6可知,6元素集合上一共可形成1+186+5325+35660+63465+25386=130023个偏序.因此,由引理2.1 可知,6元素集合上的T0拓扑个数为130023. 注本文从序与拓扑的交叉出发,基于预序集X的序和其上的Scott拓扑的特殊化序的一致性,结合Hasse图和层级配比数,给出了6 元素集合上的T0拓扑总数的计算,其结果为130023.该方法还有望向n的更大情形推广,但计算难度会越来越大.§3 若干情形讨论
3.1 含有6个极小元
3.2 含有5个极小元

3.3 含有4个极小元
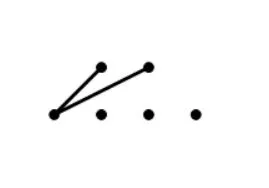

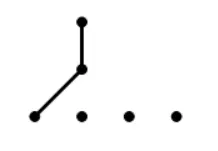

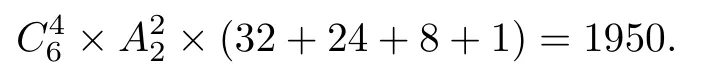
3.4 含有3个极小元

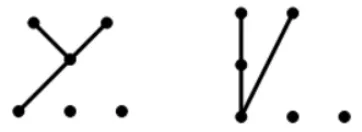


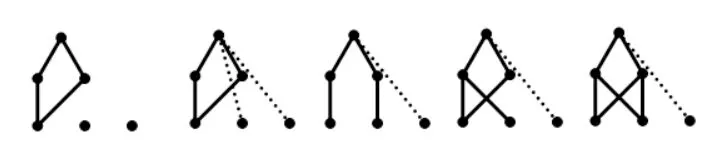
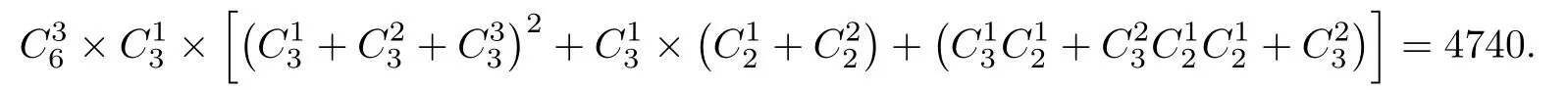



3.5 含有2个极小元







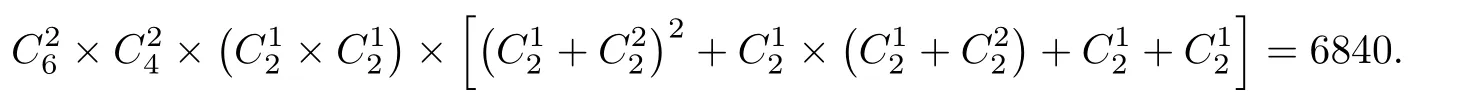
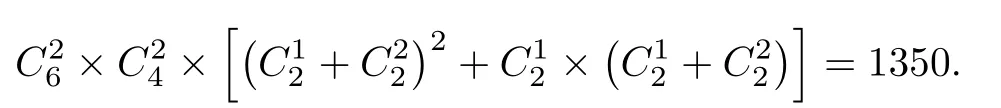


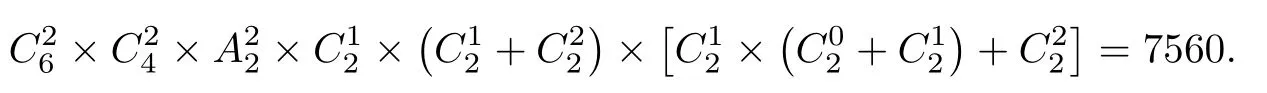


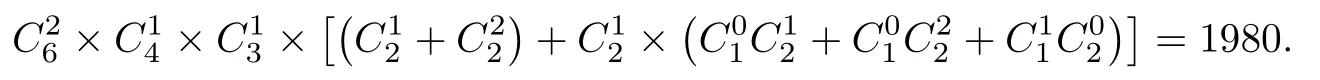






3.6 含有1个极小元

§4 主要定理的证明
