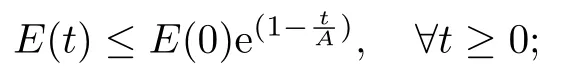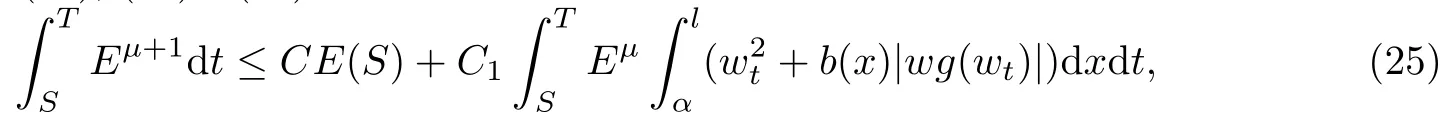一类弹性梁的能量衰减估计
2022-03-14章春国
章春国,徐 苗
(杭州电子科技大学 数学系,浙江杭州 310018)
§1 引言
随着空间科学及机器人学的日益发展,弹性梁等系统得到了广泛应用.本文旨在研究具有非线性阻尼的弹性梁振动过程中的能量变化规律,更确切地,研究非线性系统初边值问题

的能量衰减估计,这里长度为l的弹性梁在w −x平面上运动,w(x,t)表示离开平衡位置的位移,ρ,S,K是严格正的物理常数.有关该问题的技术细节请参阅文献[1-5].
假定b(x)∈C1[0,l],b(x)≥0,和

其中α(0<α 本文的研究动机源于文献Martinez[6]和Aassila[7]的工作,本文的主要工作是在反馈函数g的合理假设下,建立系统(1)的能量衰减估计.主要方法是基于非线性算子半群理论,能量摄动理论和乘子技巧(参阅文献[8-11])获得系统(1)的能量衰减估计. 以下§2陈述本文的主要结果;§3证明系统(1)的适定性;§4给出主要结果的证明. 本节首先介绍一些记号与假设,然后陈述本文的主要结果. 由于物理常数ρ,S,K是严格正的,为了方便起见,在本文中,假定ρ=S=K=1. 定义系统(1)的能量为 通过分部积分,经计算得 和 由(4)和(5)得 对∀x ∈R有xg(x)≥0,那么能量函数E(t)是单调不增,局部绝对连续的,且 并设V={u ∈H3(0,l)|u(0)=u(l)=0}具有范数 和内积 其中Hk(0,l)是k阶Sobolev空间(参见[12]). 定义H=V ×W具有范数 和内积 那么H是Hilbert空间. 为了将系统(1)纳入H上非线性发展方程的框架,定义非线性算子A 和 那么系统(1)可以改写为H上的非线性发展方程 其中Y=(w,z),Y0=(w0,z0). 为了得到系统(1)适定性和能量衰减估计,进一步假设:存在常数p ≥1以及四个正常数ci,i=1,2,3,4,使得当|x|≤1时, 当|x|>1时, 这样的g(x)是存在的,比如,g(x)=x|x|p−1. 接下来,叙述本文的主要结果. 定理2.1(适定性)如果假设(2)和(9)-(10)成立,那么算子A生成H上强连续非线性压缩半群T(t).进一步,对∀Y0∈D(A),系统(1)存在唯一的强解Y(t)=T(t)Y0. 定理2.2如果假设(2)和(9)-(10)成立,那么系统(1)的能量具有如下衰减估计. 当p=1时, 当p>1时, 其中ω,C是两个正常数. 本节证明A生成H上的非线性压缩C0−半群T(t),进而得到系统(1)的适定性. 定理2.1的证明由于g是单调不减的C1类函数,且g(0)=0.那么A是H上稠定算子.进一步,对于∀(w,z)∈D(A),经分部积分得 这就意味着A在H中是耗散的.容易验证KerA={0}.对∀(f1,f2)∈H,解方程 从而 用w乘(13)的第二式,并在0到l积分,由分部积分及边界条件得 应用Cauchy不等式,上式结合(2)和(9)-(10)得到 这里c是某个正常数. 进而由嵌入关系H3[0,l][0,l]与Poincare不等式,有 由(13)和(16)知,存在正常数M使得 上式意味着λ=0∈ρ(A)(A的预解集),A−1是有界算子,于是A是闭的.因此得到:对于足够小的λ>0有R(λ −A)=H.所以算子A是H上的极大耗散算子. 根据非线性算子半群理论[13]的第四章定理1.4,得到A生成H上的非线性压缩C0−半群T(t).进一步,由[13]可知,对于∀Y0∈D(A),系统(1)存在唯一的解Y(t)=T(t)Y0. 本节研究系统(1)的能量衰减估计. 为了证明定理2.2,需要下面的引理. 引理4.1(见[8,定理9.1]) 设E:R+−→R+是一单调不增函数,且存在两个正常数p ≥1和A>0使得 那么,当p=1时, 当p>1时, 定理2.2的证明对(w,wt)∈D(A),用xwtEµ(t)乘以(1)的第一式并在(0,l)×(S,T)上积分(这里µ是一个正实数),于是 (18)意味着 注意到(w,wt)∈D(A),由积分中值定理,能量函数E(t)的定义和(7)得 接下来,用ηwEµ(t)乘以(1)的第一式并在(0,l)×(S,T)积分,其中η是[0,l)上单调不减函数,η ∈C3[0,l],0≤η ≤1,且 正常数ε>0充分小.从而 又注意到(w,wt)∈D(A),η ∈C3[0,l],以及η在[0,l)上单调不减,应用积分中值定理得 由E(t)的单调性,Sobolev嵌入H6(0,l)2(0,l),E(t)的定义,以及Cauchy-Schwarz不等式和Poincare不等式,有(这里及后面C在不同地方表示不同的正常数) 上式结合(20)得到 应用这些估计从(22),(23)和(24)得到 其中常数C1>0. 注意到(6)和(9),得到如下的不等式. 将上式代入(25)得 另一方面,由(6)和(10)得 因此得到 由(26)-(27)得 令T →+∞取极限得 由引理4.1知,定理2.2成立.§2 预备知识与主要结果



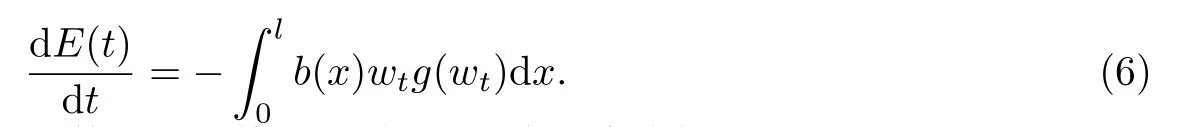











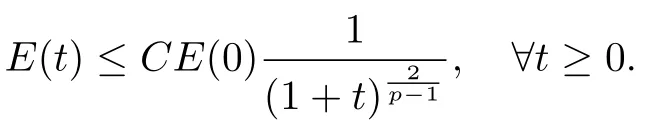
§3 适定性







§4 定理2.2的证明