基于摩擦因数的齿轮动力学特征仿真分析研究

冯 伟，黄 恒，贺石中

(广州机械科学研究院有限公司设备状态检测研究所，广东 广州 510700)

0 引 言

齿轮作为在机械工业设备中必不可少的传递运动和动力的通用零件，具有尺寸小、传动效率高、传动比准确、寿命长等特点，广泛应用于各行各业的机械设备中[1]。由于在传动过程中的关键作用，齿轮的运行状态直接影响整个设备的工作情况，其本身包含了大量的摩擦学和动力学信息[2-3]。针对这些信息进行融合处理，能对设备的故障识别起到重要作用[4-6]。在齿轮副的摩擦学与动力学信息分析中，国内外开展了相关的研究。Chen[7]等分析了中心距变化对间隙的影响，考虑了中心距改变等因素对啮合刚度的影响。Liu C[8]等研究了人字齿行星齿轮传动系统的动态特性。LI[9]等建立了齿轮的摩擦动力学模型，证明其对齿轮的疲劳磨损起重要作用。邹玉静[10]等建立了斜齿轮摩擦动力学模型并采用解耦方法求解，对齿面摩擦学特性和动力学行为以及两者之间的耦合关系进行分析。王明凯[11]等建立了双渐开线齿轮传动摩擦学和动力学模型，通过分析表明摩擦学与动力学耦合作用对齿轮动力学行为影响较显著。王奇斌[12]等研究了齿距偏差对直齿轮传动系统振动特性的影响。

笔者对直齿轮在啮合过程中的摩擦学特征信息及动力学信息进行相关性分析，通过考虑摩擦因数对齿轮副啮合动力学仿真特性影响，分析了齿轮副摩擦学与动力学信息之间的耦合关系。

1 齿轮副的摩擦学特征信息

根据对齿轮副相对运动特征的分析，对于两个齿轮构成的直齿渐开线齿轮传动系统，在相互啮合滑动过程中，从动齿轮相对于主动齿轮齿面的滑动方向总是背向节点，压力沿着齿顶方向而逐渐增大。相对应的，主动齿轮相对于从动齿轮的滑动方向则是朝向节点，而压力则沿着齿顶方向而逐渐减小[13]。两齿轮齿廓在啮合点处线速度的大小和方向均不相同(节点处除外)，则在齿廓间会存在相对滑动，并且相对运动速度的大小与啮合点的位置有关。由于相对运动的存在，将导致两齿轮在齿廓之间产生摩擦，从而使得齿面发生磨损。不仅影响齿轮系统的传动精度和效率，造成齿轮系在工作过程中的振动、噪音以及摩擦发热，而且随着磨损的逐渐加剧，会引起齿表的疲劳点蚀与剥落，甚至导致轮齿断裂。

齿轮副的摩擦学特征信息主要包括两齿轮在啮合过程中的摩擦力的变化特征信息，主要包括摩擦力的大小与方向两个方面。图1所示为齿轮啮合过程中齿面摩擦力的方向。主动轮所受摩擦力的方向背离节线，而从动轮所受摩擦力的方向则是朝向节线。若润滑不良，则有可能造成齿面材料塑性变形或者流动，引起摩擦因数的改变，从而造成齿面磨损。

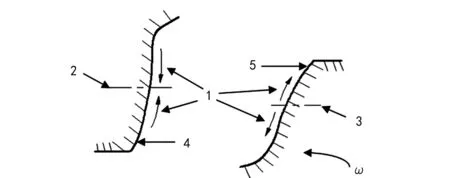
图1 齿轮副摩擦力方向示意图1.摩擦力方向 2，3.节线 4.从动齿轮2齿表 5.主动齿轮1齿表

2 齿轮副的动力学特征

齿轮副作为一个振动系统，根据传动特点，一对直齿圆柱齿轮扭振物理模型可以简化为如图2所示。

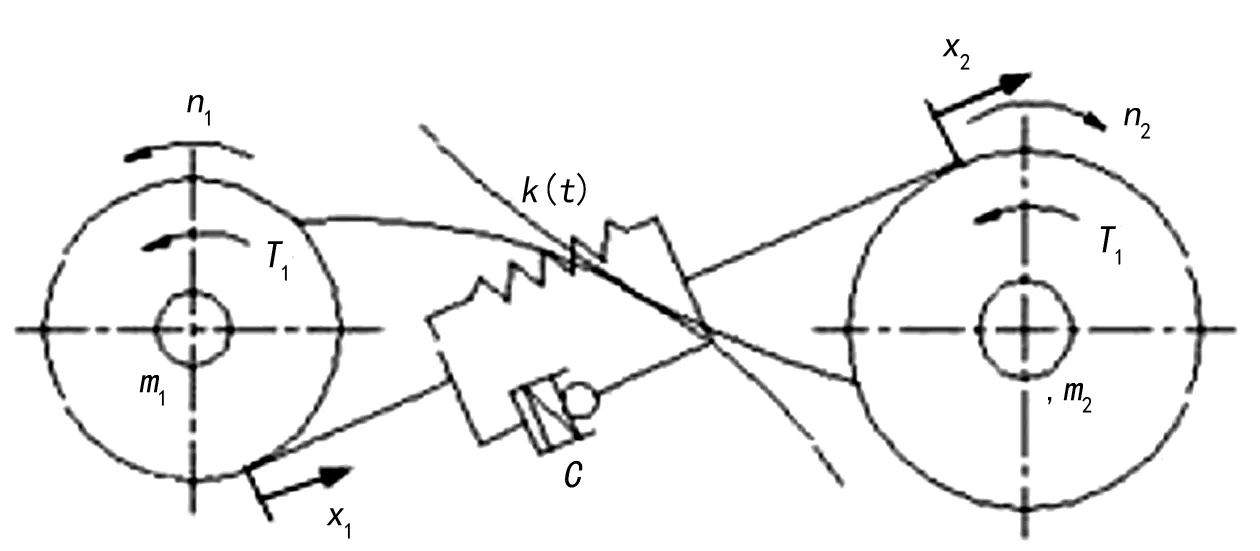
图2 齿轮传动扭振物理模型

图中2为主动轮，2为从动轮，n1、n2为主、被动齿轮的转速。根据振动理论，齿轮副动力学方程可以写成如下公式：

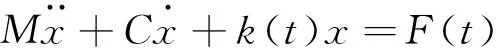
(1)

式中：M为齿轮当量质量，M=(m1m2)/(m1+m2)；x为啮合线上齿轮相对位移；C为齿轮啮合阻尼；k(t)为齿轮啮合刚度；F(t)为动载荷，包含齿表故障缺陷产生的动态激励，受轮齿啮合刚度、传动误差和齿面摩擦力方向等因素影响。如果忽略齿轮之间的摩擦力不计，方程(1)可以写为：

(2)

式中：E1为齿轮在载荷作用下的平均静弹性变形；E2(t)称为故障函数，表示齿轮的误差和故障造成的两个齿轮间的相对位移。

齿轮故障函数E2(t)由两部分组成，一部分为啮合误差，另一部分为旋转误差。齿轮误差函数可以写为：

(3)

式中：A为齿轮旋转误差的幅值；Bn为齿轮啮合误差的幅值；φn齿轮啮合误差相位；ωr为齿轮旋转角速度；ωk为齿轮啮合角速度。

齿轮啮合刚度k(t)的变化是齿轮系统振动的重要激振源之一，它是一个周期性的变量，随着齿轮啮合点位置和参加啮合的齿数的变化而变化。设t=0时为齿轮副处于双啮合状态，将k(t)展开为Fourier级数得：

(4)

式中：Ck为齿轮啮合刚度谐波；φn′为齿轮啮合刚度谐波相位。

3 变摩擦因数的齿轮动力学特征信息仿真研究

针对以上对齿轮副的摩擦学和动力学的特征信息分析研究，为了进一步了解摩擦学信息对动力学信息的影响规律，文中使用ADMAS软件进行仿真，分析两者之间的影响。采用如图3所示的常规汽车变速箱的3档齿轮系进行啮合建模。

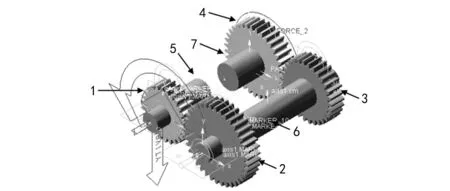
图3 齿轮系仿真物理模型1.齿轮1 2.齿轮2 3.齿轮3 4.齿轮4 5.输入轴 6.中间轴 7.输出轴

模型中的各结构参数如下：齿轮1的齿数为z1=26，齿轮2的齿数为z2=38，齿轮3的齿数为z3=30，输出轴上齿轮4的齿数为z4=35，模数m=3.75 mm，齿宽b=30 mm。设置各齿轮的质量及转动惯量为：m1=1.729 kg；m2=3.721 kg；m3=2.309 kg；m4=3.153 kg；I1=2.064·10-3kg·m2，I2=9.448·10-3kg·m2，I3=3.663·10-3kg·m2，I4=6.795·10-3kg·m2。在使用ADAMS仿真计算时，设置齿轮1、2之间的重合度ε1=1.662 1，齿轮3、4之间的重合度ε2=1.670 1，弹性模型e=206 GPa，泊松比r=0.3。节点啮合处单齿对啮合刚度为kd1=2.16×108N/m,kd2=2.19×108N/m，双齿对啮合平均刚度为ks1=3.23×108N/m，ks2=3.29×108N/m。力指数取值为2.2，阻尼系数为10 N·s/mm；阻尼力过渡区间取0.1 mm；静态阻力滑移速度取0.1 m/s；动态阻力转化速度取1.0 m/s。

3.1 速度分析

首先通过仿真计算分析齿轮系运动过程中达到动平衡时角速度大小随摩擦因数变化的关系。在主动轮1所在的输入轴上分步施加主动转矩250 N·m，从动轮4所在的输出轴上同步施加负载转矩为200 N·m。步长取0.000 1 s，仿真时间为10 s。考虑到齿面间摩擦力的影响，取静摩擦因数为0.3，动摩擦因数则取值μ1=0.05，μ2=0.10，μ3=0.15。所得到的关系变化如图4所示。

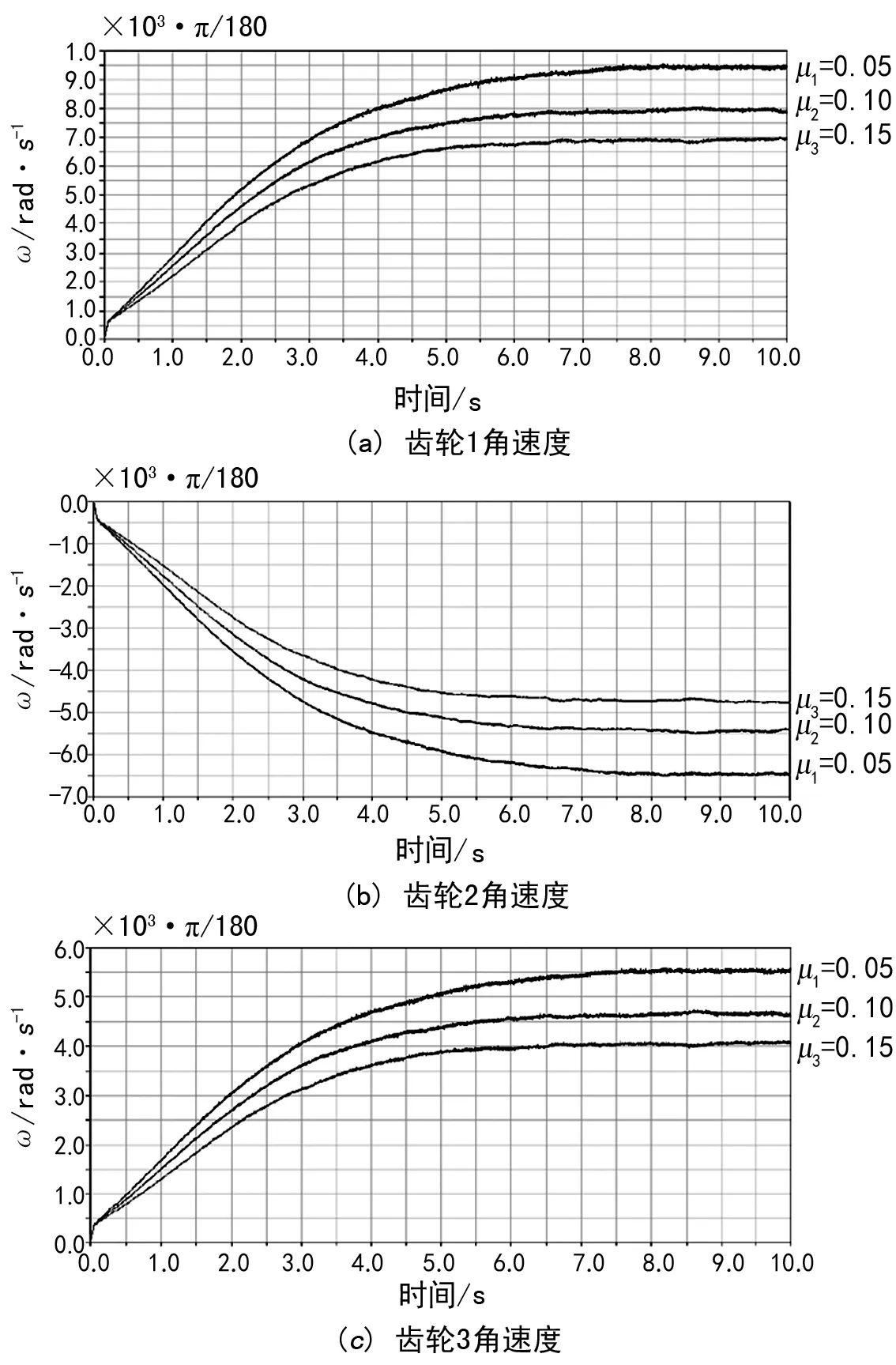
图4 齿轮角速度随摩擦因数变化曲线图

从图中可以看出，在启动初期，齿轮副受到的启动转矩较大，从而造成转速迅速增大。随着时间继续增加，在8s前，转速也随着转矩的增 加而相应增大。并且在整个过程中，随着摩擦因数的增大，各级齿轮的转速是减小的。而在8 s后，齿轮系的运动逐渐达到了平衡状态，转速保持恒定，这个平衡状态是动态的。对8 s后的曲线变化进行观察可知，各齿轮的转速是在一定范围内进行周期性波动，截取图1中μ1=0.05，8 s后的转速变化曲线进行放大如图5所示。

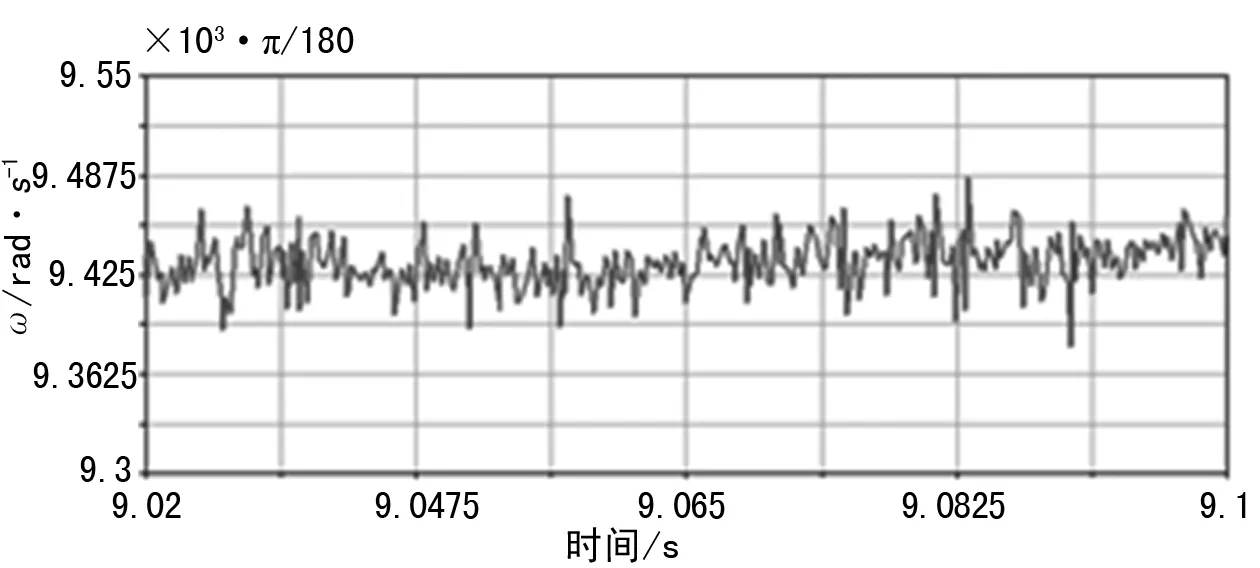
图5 平衡时齿轮1角速度变化曲线

图5可看出，齿轮的转速在一定范围内发生周期性波动，这主要是齿轮在传动过程中的振动与啮合冲击导致的。对于μ1=0.05的情况，在ADAMS软件中对齿轮在8 s后的转速计算平均值分别为164.5 rad/s,112.6 rad/s,96.5 rad/s，所得到的转速比符合传动比的要求。

3.2 啮合力仿真分析

其次针对齿轮系在不同摩擦因数条件下啮合力的变化情况。设置仿真条件为：输入功率为42 kW，在输入轴上施加转速为167.5 rad/s的驱动，并且在ADAMS中接触力step函数中设定在0.2 s内转速由0增加至167.5 rad/s。从动齿轮4所在的输出轴在0.05 s后施加一个大小为200 N·m的恒定转矩。仿真时间根据多次仿真试计算取0.3 s达到平衡，计算步长取0.000 1 s。考虑齿面间摩擦力的影响，取静摩擦因数为0.3，动摩擦因数选取齿轮系处于边界润滑状态下的值μ2=0.10。对0.3 s时间范围内齿轮系的转速变化情况进行仿真，所得结果如图6所示。

从图6中可以看出，在0.2 s前，各级齿轮的转速变化较为明显。在0.2 s后，运动达到平衡状态，输入端齿轮1的转速约为166.0 rad/s，中间轴齿轮2、3的转速约为-114.52 rad/s，输出端齿轮4的转速约为98.3 rad/s。通过计算可得，各级齿轮的转速与传动比的要求一致。

对齿轮系输入端与输出端啮合力作出时域和频域图，由于是在0.05 s后开始施加负载，故在0.05 s后才开始产生啮合力。如图7是输入端齿轮副啮合力的时域图和频域图，图8是输出端齿轮副啮合力的时域图和频域图。

图6 齿轮转速变化曲线图

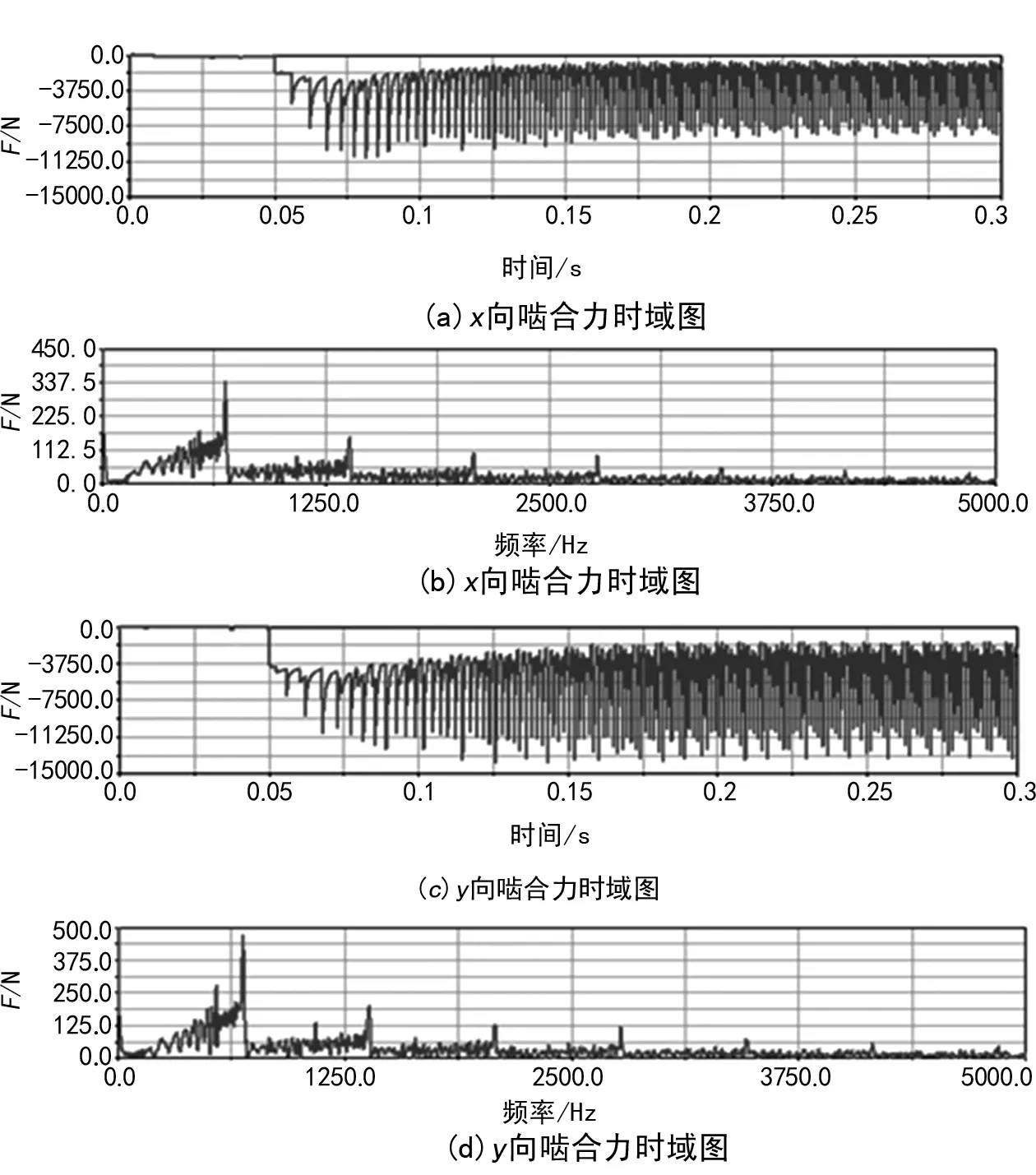
图7 输入端齿轮副啮合力时域频域图

从图8中可以看出，在0.005 s后，随着负载的增加，啮合力也开始增加，齿轮就有一定的初速度，并且在很短时间内产生一个较多的冲击。根据齿轮啮合运动的特点，在开始阶段，x向分力(径向力)逐渐增大，因此在图8(a)中表现为啮合力有一个很大的值。在0～0.2 s的过程中，径向力的周期由大变小，幅值也逐渐减小；在0.2 s后，波动趋于稳定。而对于y向分力(圆周力)，在0～0.2 s阶段，啮合力的周期由大变小，并且力的大小逐渐增加。在0.2 s后，波动趋于稳定。根据齿轮啮合过程中径向力和圆周力的理论计算公式，将算得的理论值与仿真值进行比较如表1所列。从表中可以看出，理论值与仿真值较为接近，证明仿真结果是准确的。

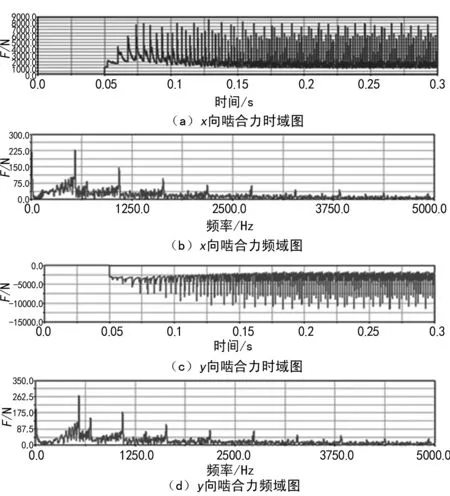
图8 输出端齿轮副啮合力时域频域图

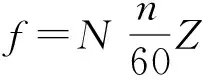
表1 啮合力数值比较

对齿轮系在不同摩擦因数的条件下，达到平衡转动时的啮合力进行仿真。如图9为齿轮在达到平衡时啮合力的曲线。从图中可以看出，轴向力和径向力都会随着齿面摩擦因数的变化而发生变化。摩擦因数越大，齿面的啮合力则相应增加。这主要是因为齿面摩擦力的方向与两齿面相对滑动速度方向相反，啮合力的大小受到摩擦因数的影响。

从图中分析可知，对于不同摩擦因数的啮合力曲线，x向啮合力偏差很小，而y向啮合力几乎重合。这说明在仿真过程中，由于齿面间磨损造成的能量损失较小，几乎可以忽略不计。而在实际啮合过程中，摩擦力所造成的摩擦损失往往会增加能量耗损，影响齿面的接触特性，从而使齿面的接触力变大。

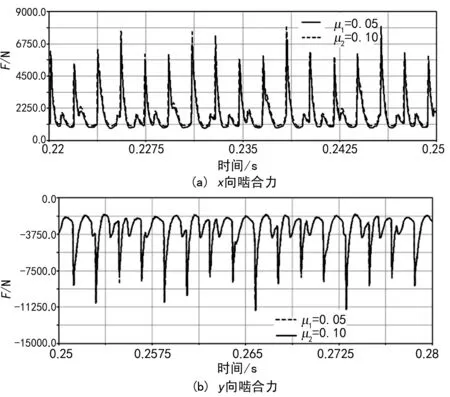
图9 输出端齿轮啮合力

5 结 论

通过对齿轮系摩擦学特征信息和动力学特征信息进行理论计算与分析，研究了两者之间的相关性，并通过ADMAS对齿轮系的动力学特征进行仿真。得到以下结论。

(1) 齿轮系的摩擦学特征信息与动力学特征信息之间存在着相关性，两者之间的特征能够对齿轮系的故障类型识别等提供基础。

(2) 齿轮啮合过程中的仿真结果表明，齿轮啮合力的仿真值与理论值之间的差值在误差范围内，并且在不同摩擦因数条件下啮合力的大小稍微发生变化，与理论计算基本一致。

(3) 通过仿真分析齿轮系摩擦磨损信息对振动的影响表明，齿轮摩擦学信息与动力学信息之间相互影响、相互渗透，在输出状态特征过程中表现出较强的耦合性。