基于有限元的动车组车体结构疲劳强度分析方法研究

韩 威，杨 杏，李 刚，马文瑞

(1.陕西铁路工程职业技术学院，陕西 渭南 714000； 2.兰州交通大学 机电工程学院，甘肃 兰州 730070；3.中车唐山机车车辆有限公司 产品研发中心，河北 唐山 063000)

0 引 言

随着动车组运行时速的提升，对车辆运行过程中的可靠性要求越来越高。车体作为动车组结构的核心部位，其强度是否符合要求直接关系着整个动车组的运行安全。

动车组在运行过程中其车体所承受的动态载荷复杂多变，保证动车组安全运行的关键是其车体结构疲劳强度满足设计要求。当动车组运行时速在200 km以上时，车体结构疲劳强度受机械载荷影响比重变得越来越小，受气动交变载荷的影响越来越大[1]。笔者通过对机械、气动交变载荷影响下的动车组车体结构强度的研究得出车体强度满足设计要求具有非常重要的意义。

1 头车车体的结构及其有限元模型

1.1 车体的几何模型

CRH3型动车组是由唐山轨道客车有限公司研发制造，其车体结构为焊接铝合金型材结构，型材厚度最低处约为1.5 mm，且长度最长可达十几米。在对车体进行有限元分析网格划分时需要将车体的每一部分划分为一个单元，这样做结果会导致铝合金车体结构网格划分过度细密，计算量过大。为此，在建立车体几何模型时选择将实际的中空结构等效为实体结构[2-3]，通过计算并验证保证等效厚度和实体厚度其强度和刚度等效。车体各个部位中空结构的实际厚度与等效后的实体厚度如表1所列，建立头车车体的三维实体几何模型如图1所列。

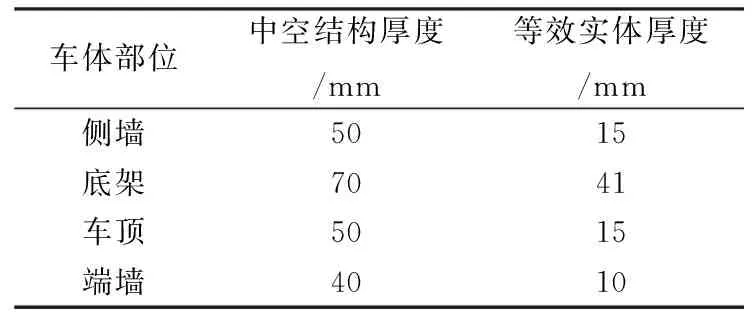
表1 车体实际厚度和等效厚度

1.2 车体的有限元模型

将已建立好的车体几何模型导入Workbench，并运用其网格划分Meshing工具对车体结构进行离散化处理。由于车体的装配体结构比较复杂，因此采用自动网格划分法，车体结构离散化得到的有限元模型如图2所示。

图1 CRH3头车车体三维模型

图2 头车车体的有限元模型

2 有限元仿真计算及车体结构疲劳强度分析

2.1 车体疲劳载荷工况的确定

欧洲标准EN12663：2000规定，在对车辆车体等进行强度分析时，不仅只对气动载荷进行分析，须综合考虑到牵引制动、轨道条件、轨缝处的轮轨冲击以及轨道变形引起的疲劳载荷，对车体的各方向震动疲劳载荷须取经验值[4]。因此车体纵向疲劳载荷fxd、横向疲劳载荷fyd和垂向疲劳载荷fzd计算公式如下：

fxd=fyd=fzd=0.15 mg

(1)

高速动车组在运行时在周围会产生强烈的空气波，尤其是当会车或通过隧道时，空气波会急剧加大，而会车时车体的会车一侧会产生极高的空气压力波载荷。车体疲劳载荷分析从明线会车、隧道通过和隧道会车三个工况来进行，此处以明线会车工况详细说明，另两种工况分析方法相同。

设定相向行驶的两辆动车组其线间距为4.4 m，车速为300 km/h，当两辆动车组明线会车时其头车车体所受压力波如图3所示。

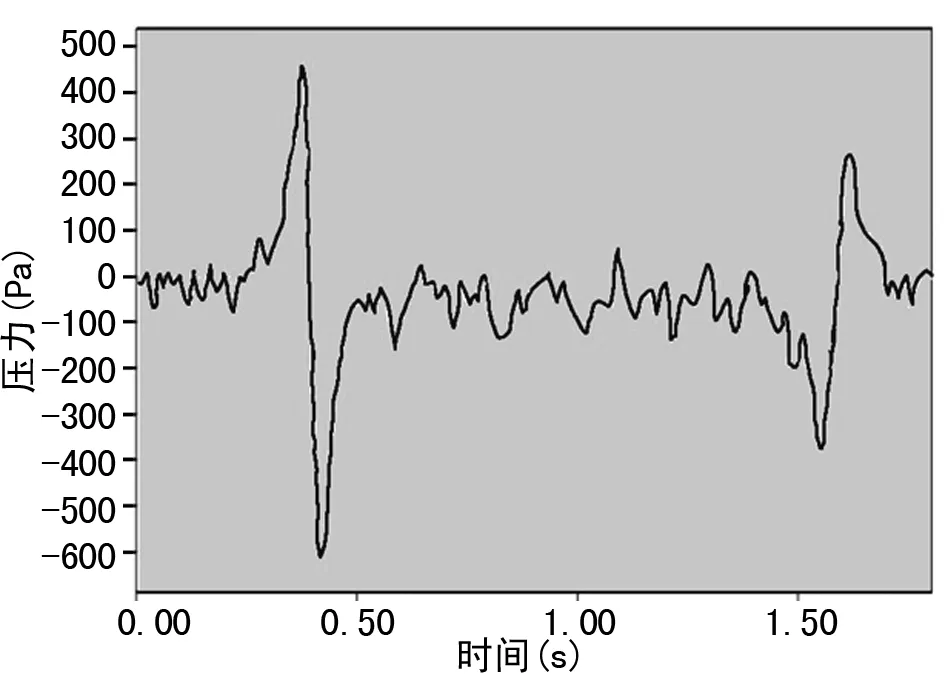
图3 明线会车时车体的压力波曲线图

为对压力波作用在车体上的实际过程进行仿真，可将车体沿车场方向分为6个区域，分别为6个分区。将图3中的车体压力波作用过程通过Workbench沿车长方向分别对6个分区做瞬态分析。具体分析过程为：会车前车体各分区均不受压力波载荷作用，此为时间步1；从0.25 s开始压力波到达分区1未达分区2，此时仅分区1承受压力波，为时间步2；接着0.28 s时压力波到达分区2，此时分区2开始承受分区1刚才所受压力波，而分区1则承受压力波曲线上下一时间点的压力波，其它分区压力波还未到达，为时间步3；然后压力波依次先后到达分区3～6，并同样扫掠过每一分区，直至压力波沿纵向扫掠过整个车体表面时结束，详细加载过程如表2所列。

表2 压力波加载时间步说明 /Pa

2.2 有限元仿真计算

在 Workbench的瞬态分析模块中，将表2中确定的气动疲劳载荷时间步和由公式(1)计算的机械疲劳载荷施加到已建立的车体有限元模型上。定义车体各部分主要材料的密度和力学性能参数如表3所列，设置求解时间和输出等控制，计算出车体在压力波作用过程中最大和最小主应力时间历程，计算结果如图4所示。

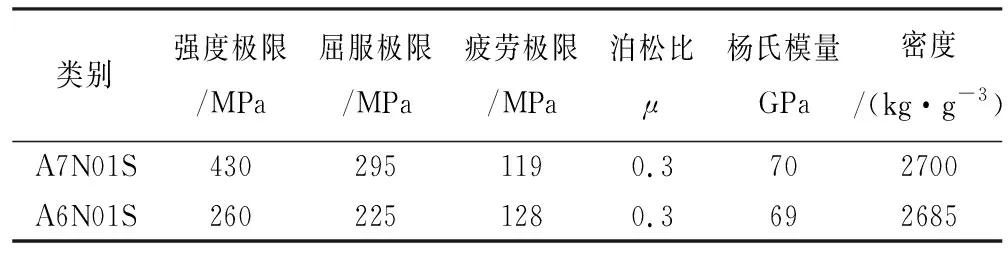
表3 车体材料性能参数

2.3 车体结构疲劳强度分析

根据我国《200 km/h及以上速度级铁道车辆强度设计及试验鉴定暂行规定》中要求，在对车体结构进行疲劳强度分析时，可选取Goodman疲劳极限图作为车体疲劳强度分析的评定根据[5]。由于动车组在运行过程中既受气动载荷的影响，还会受到制动摩擦、震动等交变机械载荷的影响，因此车体处在多轴应力状态，需将多轴应力转变为单轴应力。

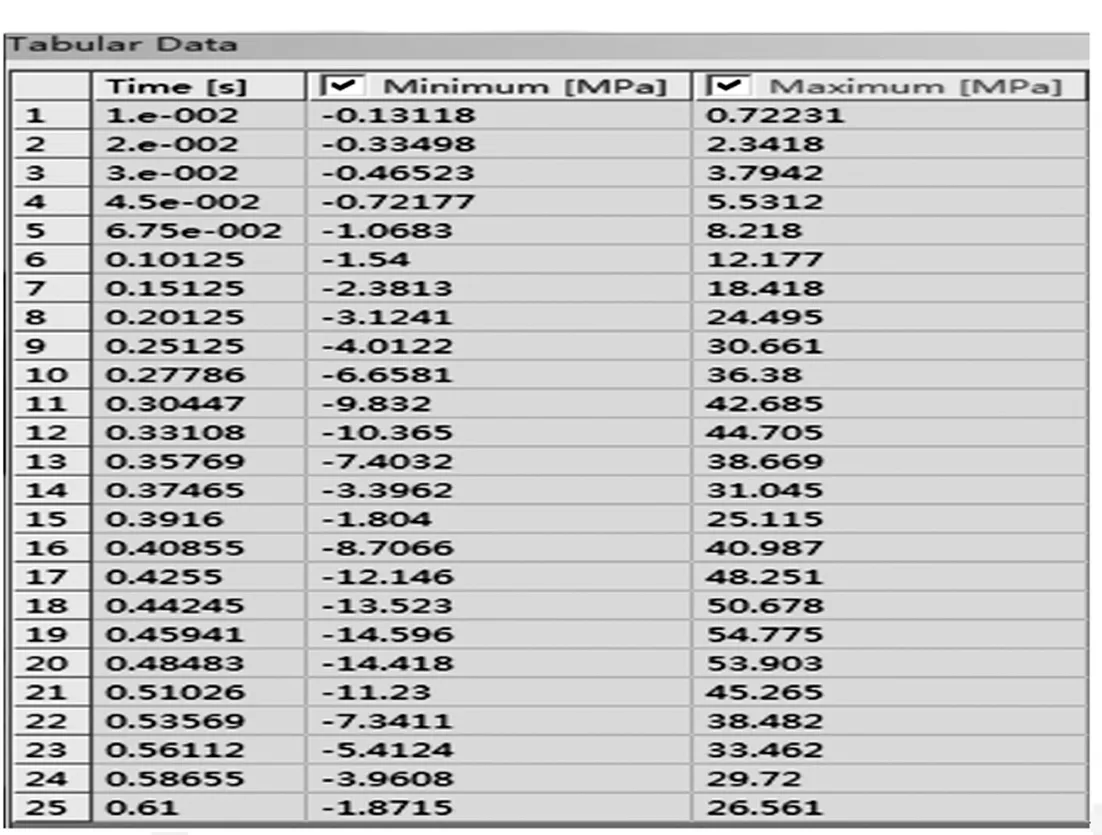
图4 车体最大和最小主应力时间历程截图

此处采用最大主应力法将多轴应力状态转变为单轴应力，具体方法为：分别对车体在受到不同载荷作用下的应力进行计算，选取应力最大时的应力方向确定为最大主应力方向，应力值为最大主应力σmax，将受到其它载荷作用的应力投射到最大主应力方向取其值为最小主应力σmin，后可确定应力幅值和应力均值为：

(2)

(3)

将图4中所有时间点的最大主应力σmax和最小主应力σmin带入到公式(2)和公式(3)中计算出应力幅值σamp和应力均值σmean，然后以每一时间点的σamp为纵坐标、σmean为横坐标在车体主要材料的Goodman疲劳极限图内描点，结果如图5所示。

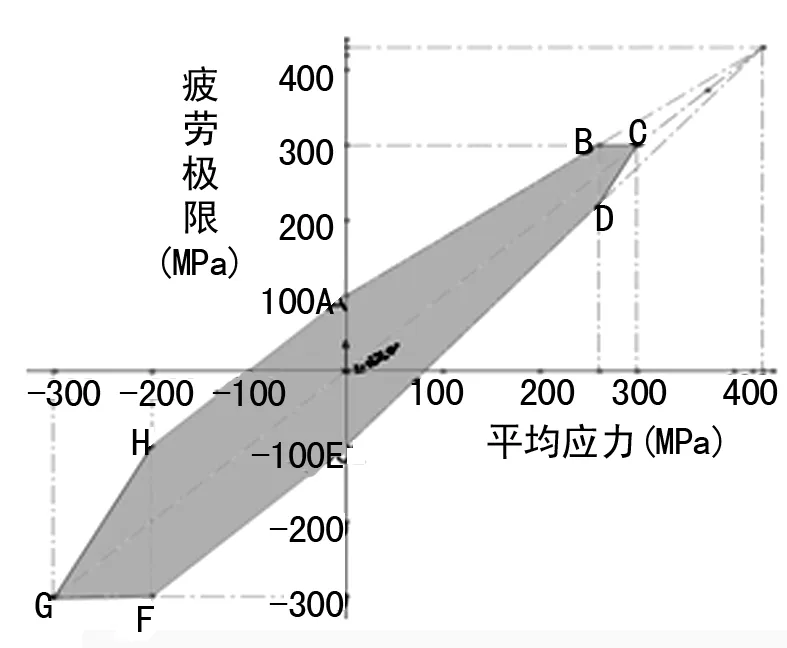
图5 明线会车时车体疲劳强度分析图

由图5可知，疲劳载荷作用过程中所有时间点的应力幅值σamp和应力均值σmean均在包络线ABCDEFGH的内部，因而车体的疲劳强度满足设计要求，车体结构在设计的使用寿命内不会发生疲劳破坏[6-7]。根据相同方法对隧道通过和隧道会车两种工况进行车体疲劳强度分析，分析结果如图6、7所示，从图中亦可以看出，疲劳载荷作用过程中的所有时间点其应力幅值和应力均值均在包络线内部，因此车体疲劳强度满足设计要求。

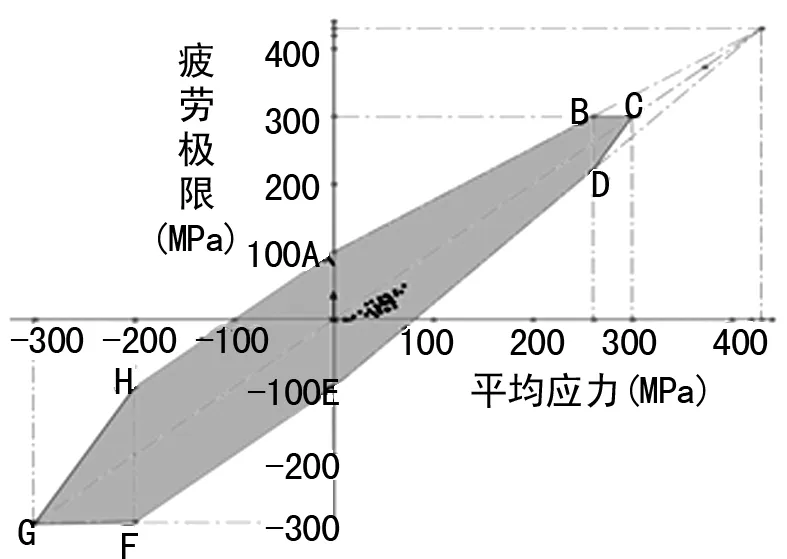
图6 隧道通过时车体疲劳强度分析图

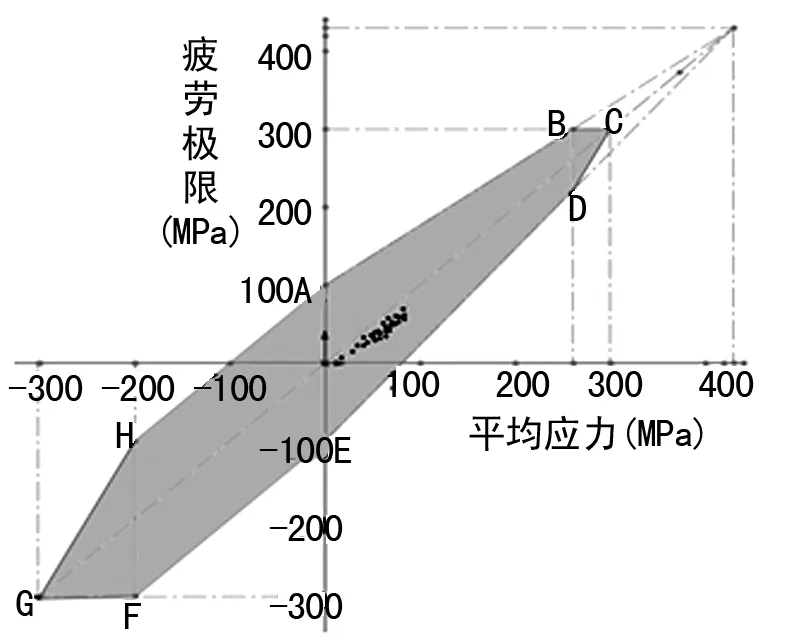
图7 隧道会车车体疲劳强度分析图

3 车体结构疲劳寿命预测

3.1 车体材料的S-N曲线

S-N曲线是描述一定循环条件下疲劳强度与疲劳寿命之间关系的曲线，是进行车体材料寿命估算的关键依据，在工程中常用来估算结构的疲劳寿命[8-9]。CRH3动车组车体主要材料为A7N01S和A6N01S，计算动车组车体主要材料的S-N曲线如图8所示，其中置信度为95%，存活率为99%。

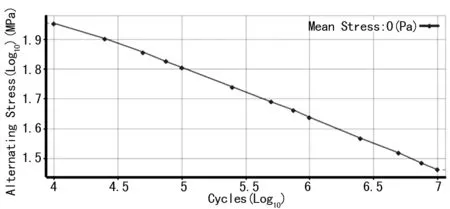
图8 动车组车体主要材料的S-N曲线

3.2 车体疲劳寿命的计算及结果

动车组车体疲劳寿命与其所受到应力幅值密切相关，且其疲劳过程属于高周疲劳，因此在进行疲劳寿命计算时选择基于应力的疲劳程序模块Stress Life[10-11]，疲劳强度因子设为0.8，具体设置如图9所示。通过有限元瞬态动力学分析，对车体的疲劳寿命(Life)、安全系数(Safety Factor)及疲劳损伤值(Damage)进行计算。

通过有限元计算得到的车体的疲劳寿命云图如图10所示，从图中可以看出，车体结构疲劳寿命的最小值为1.74e6，最大值为1e7，因此能够满足车体设计要求(安全运行20年)。计算车体的安全系数云图如图11所示，从图中可以看出车体的最小安全系数为1.15，大于标准值1，因此可确定车体的安全系数亦满足要求。计算车体的疲劳损伤云图结果如图12所示，从图中可以看出车体的最大疲劳损伤值为0.574，远小于标准值1，因此可确定车体在运行过程中不会发生疲劳破坏。

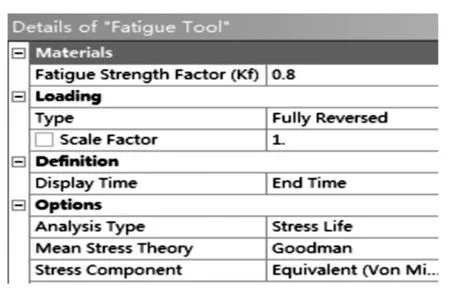
图9 疲劳寿命计算设置

图10 车体疲劳寿命云图

图11 车体安全系数云图

图12 车体疲劳损伤云图

4 结 语

以CRH3型车头车为原型建立车体几何模型，将模型导入到Workbench中，对明线会车、隧道通过、隧道会车三种工况进行疲劳强度分析，分析结果证明三种工况下疲劳载荷作用过程中的所有时间点，其应力幅值和应力均值均在包络线内部，车体疲劳强度满足设计要求。结合有限元仿真计算的结果，运用车体主要材料的Goodman疲劳极限图对车体结构的疲劳强度进行分析，并对车体安全使用寿命进行计算。仿真结果表明，车体各部位的安全系数均大于1，满足疲劳强度的要求，车体结构的疲劳寿命也满足设计要求。