农用柔性底盘前轮转向动力学研究
2022-03-14周福阳郭康权张新月贾祎涵舒成勇
周福阳 郭康权 张新月 贾祎涵 舒成勇
(西北农林科技大学机械与电子工程学院, 陕西杨凌 712100)
0 引言
农用柔性底盘通过偏置的轮毂电机驱动行进,省去了专用转向电机,通过偏置转向轴和电磁摩擦锁机构将轮毂电机驱动力转换为转向力矩实现转向,是一种四轮独立驱动、四轮独立转向底盘[1-11]。它可以实现前轮转向、四轮转向、原地回转、横行等运动模式,具有结构简单、转向灵活、无排放等优点,便于温室、仓库等狭小封闭环境运行作业。对于解决我国设施农业机械化水平低、动力机械缺乏等具有现实意义[12-14]。柔性底盘前轮转向过程中,受车体姿态与车速、各转向轮转向角匹配关系的影响。需要进行整车动力学分析,探明柔性底盘的转向特性,为控制策略的制定提供依据。
SONG等[9]基于试验台架对柔性底盘的动力学特性进行了仿真和试验;文献[10-11]对柔性底盘的四轮转向运动进行了建模和仿真试验,文献[10]的各轮转向角固定,文献[11]中直接设定转向角,没有考虑驱动力、电磁锁摩擦力等共同作用下的转向过程。文献[15-19]指出,线控转向系统存在系统参数不确定性以及轮胎非线性等问题,因此采用了模糊逻辑、神经网络、自适应和滑模等控制方法,确保对目标转向角的可靠、准确跟踪。相比普通线控转向系统,柔性底盘转向力矩来自于轮胎与地面之间的作用力;各转向轮的转向在机械上独立,前轮转向时需要对两转向轮的转向角进行关联控制,使之满足阿克曼转向几何关系。
本文通过动力学仿真对柔性底盘前轮转向特性进行研究,并进行实车验证,以期为两轮独立转向控制策略的制定提供仿真平台与理论依据。
1 柔性底盘动力学仿真模型建立
1.1 柔性底盘结构
柔性底盘主要由车架和4个相对独立的基于偏置转向轴的转向驱动单元组成(图1)。其中电磁摩擦锁定片、偏置转向轴与车架固连,电磁摩擦锁动片、偏置臂、减震机构及电动轮固连,构成一个转向驱动单元。偏置转向轴轴线与轮胎回转平面存在偏置距离,当摩擦锁锁紧时,驱动单元和车体之间的相对位置固定,车轮保持原有的转角;当电磁锁摩擦力矩小于转向力矩时,转向驱动单元转角相对车体变动,使车辆转向。

图1 柔性底盘实物图Fig.1 Prototype of flexible chassis1.偏置臂 2.电动轮 3.减震器 4.电磁摩擦锁动片 5.电磁摩擦锁定片 6.直流开关电源 7.电控系统 8.车架
1.2 运动学分析
柔性底盘行驶速度较低,忽略车体的侧倾与俯仰,忽略车轮的侧倾、振动、滑移,只考虑车辆的纵向、侧向和横摆运动,车辆运动简化为平行于地面的平面运动。
模型的坐标系包括1个固定的大地坐标系与4个随车运动的转向驱动单元坐标系。图2中点A、B、C、D为右前、左前、左后、右后偏置转向轴的中心,同时也是相应转向驱动单元的序号。大地坐标系OGXYZ固定于地面,坐标原点OG与车辆初始位置质心O重合。X轴平行于车辆初始位置时车体的纵向轴线,Z轴垂直地面向上,Y轴指向驾驶员左侧。转向驱动单元A(右前转向驱动单元)坐标系为OAwτnξ。其中OAw位于车轮中心,纵向τ指向车轮前进方向,垂向ξ垂直于地面向上,法向n指向车辆左侧。转向驱动单元B、C、D坐标系的定义与转向驱动单元A类似,具体如图2所示。

图2 柔性底盘坐标系与运动学分析Fig.2 Coordinate system definition and kinematic analysis of flexible chassis
一组广义坐标可以完整描述物体运动状态,其个数等于自由度。图2中,选择车辆质心坐标x、y以及车辆转动角θ,转向驱动单元A、B、C、D的转动角θA、θB、θC、θD为一组广义坐标(各转向驱动单元转动角等于相应车轮的转动角,所有转动以逆时针方向为正),即柔性底盘的自由度为7。根据广义坐标,通过速度与加速度合成方法,可以求得各转向中心、转向驱动单元质心及车轮中心在其横向与纵向的速度或加速度为
(1)
(2)
(3)
(4)
(5)
(6)
(7)
其中
(8)
式中viwn——车轮i中心横向速度,其中i分别表示A、B、C、D,下同
δi——车体对角线与转向驱动单元i横向的夹角
δ——车体对角线与车体横向的夹角
d——车体对角线长度的一半
viwτ——车轮i中心纵向速度
ain——转向中心i横向加速度
aiτ—— 转向中心i纵向加速度
aicn——转向驱动单元i质心横向加速度
aicτ——转向驱动单元i质心纵向加速度
Lc——转向驱动单元质心到其转向中心距离
εiw——车轮i轮胎滚动角加速度
L——偏置距离,转向中心到轮胎中心水平距离
R——轮胎滚动半径
各轮胎的侧偏角βiw为
βiw=arctan(viwn/viwτ)
(9)
1.3 动力学分析
1.3.1轮胎侧向力、纵向力与回正力矩
柔性底盘运动姿态、行驶方向的改变是轮胎与地面作用的结果,因而轮胎力学模型影响系统的性能。研究表明:车辆正常行驶,侧向加速度不超过3.92 m/s2,侧偏角不超过5°,轮胎侧偏特性处于线性范围[20],即轮胎的侧向力和回正力矩正比于轮胎侧偏角。根据轮胎线性模型,车轮i轮胎受到的侧向力Fiwn为
Fiwn=kβiw
(10)
式中k——轮胎侧向刚度,为负数
车轮i轮胎回正力矩Mia为
Mia=-Fiwne
(11)
式中e——轮胎拖距
当侧偏角较小,轮胎接地印迹后部没有滑移时,回正力矩与侧偏角呈线性关系,e不变,等于轮胎接地印迹长度的1/6[21]。
将车轮绕质心转动动量矩方程等式变换,即得到车轮i轮胎纵向力Fiwτ方程为
Fiwτ=(Miw-Jwεiw-Mwr)/R
(12)
式中Jw——车轮绕其质心的转动惯量
Miw——车轮i的驱动力矩,为控制量
Mwr——车轮滚动阻力矩
1.3.2转向驱动单元转动角加速度
根据各转向驱动单元绕其转向中心相对转动的动量矩公式(其转向驱动单元B的动力学分析如图3所示),经简单变换,得到各转向驱动单元转动角加速度方程为
(13)
式中Jg——转向驱动单元相对于转向中心的转动惯量
Mir——转向驱动单元i电磁锁实际摩擦阻力矩
mg——转向驱动单元质量
其中mgLcaiτ为转向中心加速度造成的附加转向力矩。
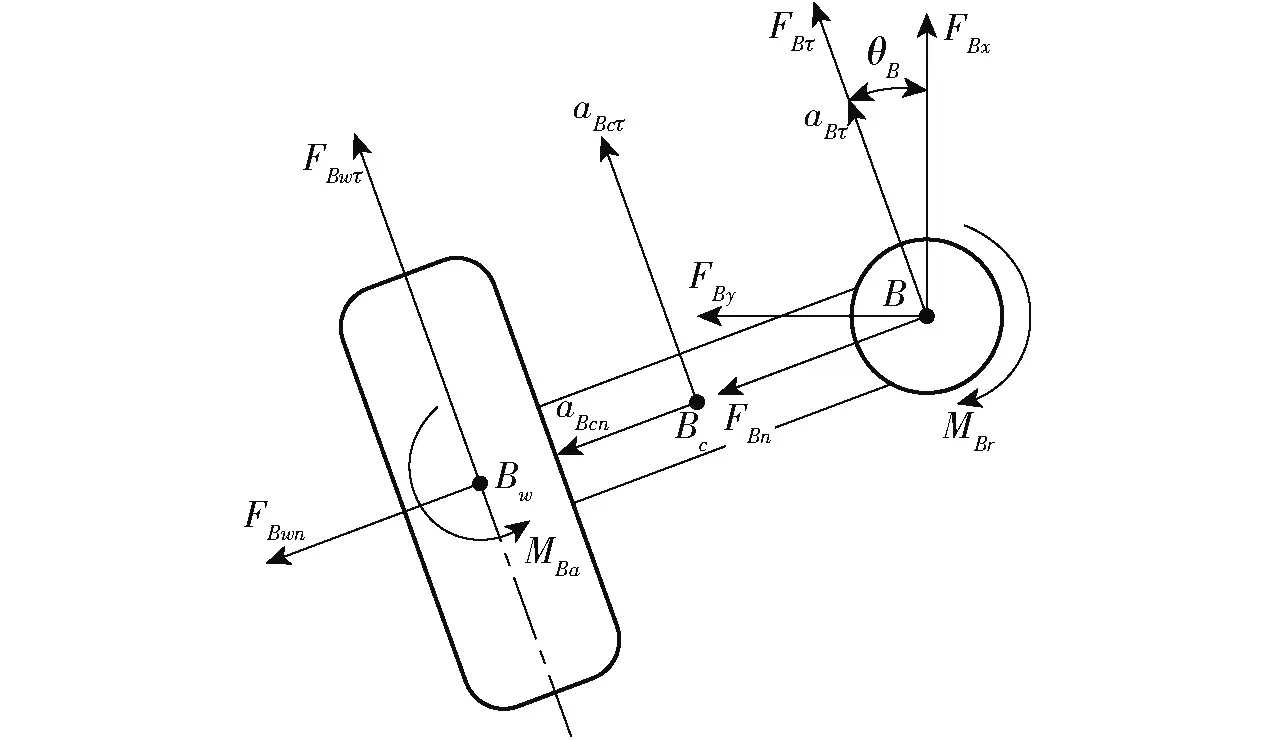
图3 转向驱动单元B和转向中心B的受力分析Fig.3 Force analysis of steering and driving unit B and steering center B
1.3.3转向中心受力
车体与转向驱动单元之间相互作用的力可以简化为作用在转向中心的2个力和1个力矩。根据各转向驱动单元沿其纵向与横向加速度方程(转向中心B受力分析如图3所示),求得车体作用在其转向中心处的纵向力Fiτ与横向力Fin为
Fiτ=mgaicτ-Fiwτ
(14)
Fin=mgaicn-Fiwn
(15)
车体受到的各转向驱动单元的反作用在其转向中心的X方向分力Fix与Y方向的力Fiy为
Fix=Finsinθi-Fiτcosθi
(16)
Fiy=-Fincosθi-Fiτsinθi
(17)
1.3.4车体动力学方程
车体受到的所有水平面上的力与力矩都来自于各转向中心,对车体进行动力学分析(图4),得
(18)
(19)

(20)
式中m——车体质量
J——车体绕质心的转动惯量

图4 车体动力学分析Fig.4 Kinetics analysis of vehicle body
通过电流可以调整电磁摩擦锁的最大摩擦力矩。根据文献[22-23],结合本文实际得到电磁锁摩擦阻力矩Mir方程为
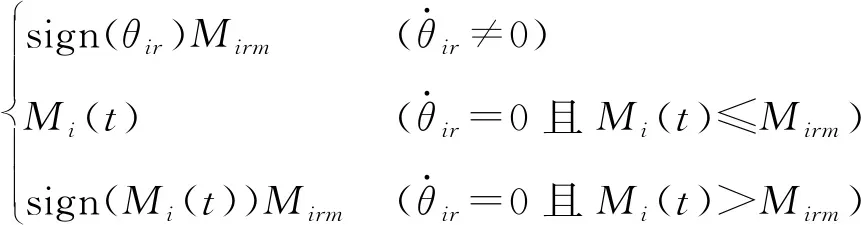
(21)
式中Mirm——电磁摩擦锁i的最大摩擦力矩,由电磁锁线圈电流控制
Mi(t)——t时刻转向驱动单元受到的其他所有转向力矩之和
θir——转向驱动单元i相对车体的转动角,即转向驱动单元转向角,它与车轮转向角相等,其值等于该轮转动角减车体转动角
1.4 仿真模型与仿真参数设置
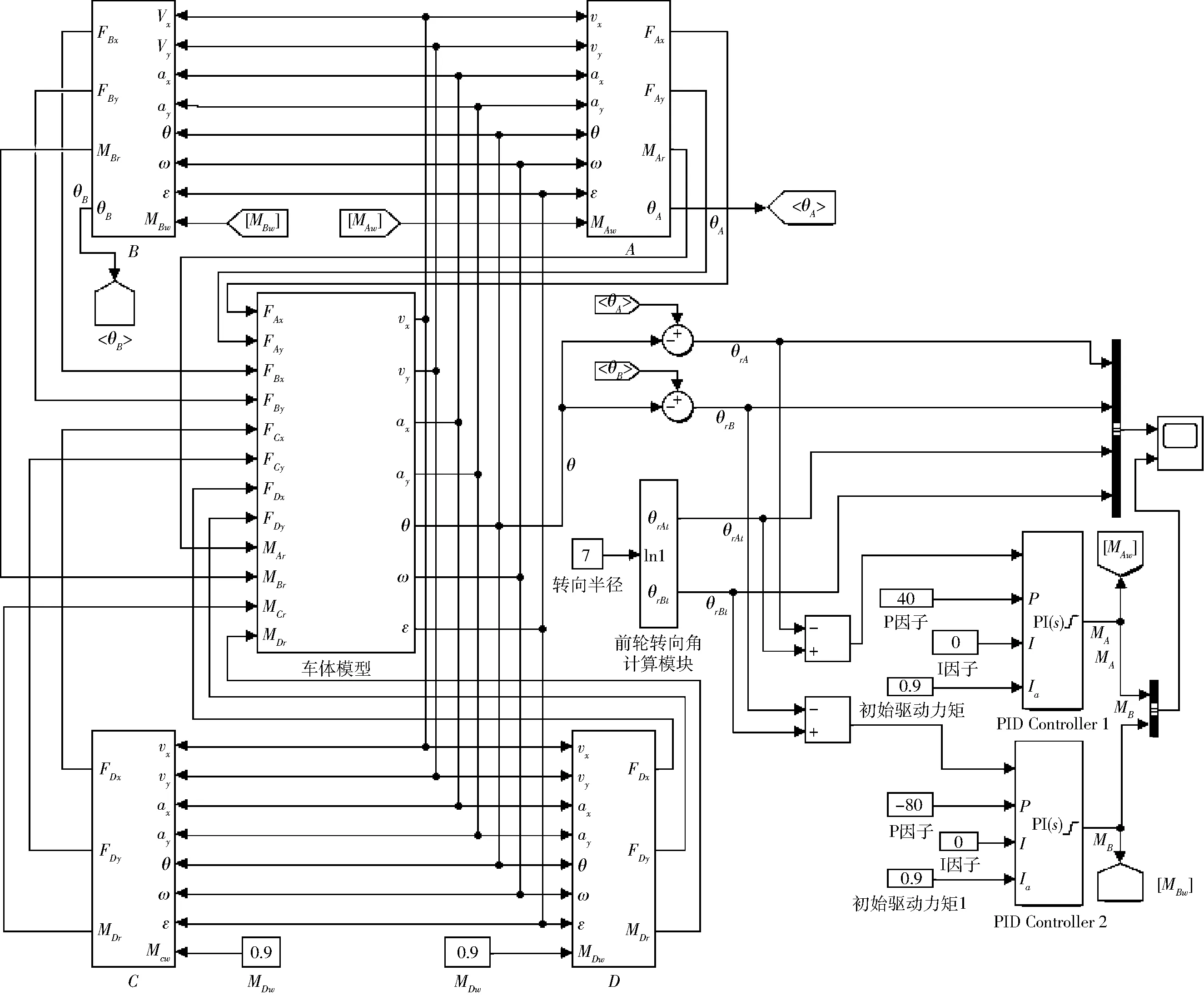
图5 基于Simulink的柔性底盘动力学仿真模型Fig.5 Dynamics simulation model of flexible chassis based on Simulink
式(1)~(21)为一组二阶微分代数方程组,构成了完整的柔性底盘整车动力学模型,输入各轮驱动力矩Miw与各电磁锁最大摩擦力矩Mirm,即可通过该方程组计算得到每一时刻柔性底盘各处的运动状态与受力情况。为求解方程组,使用Matlab/Simulink工具箱,根据式(1)~(21)建立柔性底盘动力学仿真模型(图5),从而对动力学模型进行数值计算。
仿真模型各参数和实车一致,其中转动惯量根据与实物质量相等的SolidWorks三维实体模型得到,侧偏刚度通过低速圆周实验法测得[24]。各参数如表1所示,l为车体长度,w为车体宽度。

表1 各仿真参数Tab.1 Value of each simulation parameter
1.5 控制系统
在仿真模型中,对各轮驱动力矩Miw与各电磁锁最大摩擦力矩Mirm进行控制,即可实现柔性底盘前轮或四轮转向等运动形式的仿真。
前轮转向时,可对非关键控制量的控制进行合理简化:不参与转向的两后轮驱动力矩为0.90 N·m,等于滚动阻力矩;后轮电磁摩擦锁定;前轮电磁锁解锁后其最大摩擦力矩设置为0.84 N·m(见3.4节)。主要对两前轮的驱动力矩进行控制。
柔性底盘前轮转向过程要保持顺畅,两前轮转向角应符合阿克曼转向几何关系(图6)。图中Rat为底盘瞬时转向中心到内侧后轮转向中心的距离,该距离和转向半径接近,称为近似转向半径。根据阿克曼转向几何,近似转向半径与两前轮转向角之间的关系为
(22)
(23)

图6 符合阿克曼转向几何的柔性底盘前轮转向过程Fig.6 Front wheel steering process of flexible chassis conforming to Ackerman steering geometry
前轮转向时将近似转向半径Rat设置为控制目标,由该值通过式(22)、(23)算出两前轮的转向角。仿真系统控制如图7所示,图中Ratt为近似转向半径目标值,θrAt与θrBt分别为通过Ratt计算的轮A与轮B转向角的目标值。控制器根据各前轮目标转向角与实际转向角的偏差,控制各自驱动力矩,使实际转向角趋近目标转向角。图7中控制器设置为PI控制器。

图7 柔性底盘仿真控制系统示意图Fig.7 Schematic of flexible chassis simulation control system
2 动力学仿真分析
根据式(13),可知推动转向驱动单元转动的因素包括轮胎纵向力力矩、回正力矩、转向中心加速度导致的附加力矩以及电磁锁摩擦阻力矩。根据式(12)可知纵向力力矩主要由驱动力矩决定。当底盘左转向时,左右轮都要向正向转向,根据式(13),要求右轮纵向力为正,而左轮纵向力为负,即前轮左转向过程中要求右轮为驱动,左轮为制动。右转向反之,即转向过程要求外前轮驱动,内前轮制动。
2.1 单轮驱动转向仿真
为了分析2个前转向轮之间的相互影响,研究仅一侧前轮被轮胎纵向力推动转向的情形。即仅增加单侧转向轮的驱动力矩,另一侧转向轮驱动力矩等于轮胎滚动阻力矩(不加减速时轮胎纵向力为零)。
仿真条件为:转向初始车速10 km/h;左前轮(轮B)驱动力矩等于滚动阻力矩,右前轮(轮A)驱动力矩保持3.9 N·m。仿真结果表明,虽然只有轮A被驱动着转向,但轮B也跟着转向,最终4.4 s后,轮A转向角稳定于7.6°,轮B转向角稳定于7.2°。


图8 单轮驱动转向仿真结果Fig.8 Simulation results of single-wheel drive steering
从图8可以看到,单轮驱动转向时出现了两轮交替转向的现象。这是因为仅轮A被推动转向时,造成相对于阿克曼转向角,轮A转向角超前,而轮B转向角落后,轮A与两后轮确定的瞬时转向半径小于轮B与两后轮确定的,真实的瞬时转向中心在各自确定的位置的中间,造成两轮都出现侧偏角,出现相应的回正力矩,其中轮A回正力矩阻止转向,轮B回正力矩推动转向,说明该回正力矩具有阻止两前轮转向角偏离阿克曼转向几何的作用。根据阿克曼转向几何,在图8a中绘出了与轮A转向角相匹配的轮B理论转向角,轮B理论转向角与实际转向角的差越大,两轮偏离阿克曼转向几何的程度越大。从图8b、8c可以看出,越偏离阿克曼转向几何,两轮的回正力矩越大,反之亦然。正是这种回正力矩导致了仅轮A被推动转向时出现两轮交替转向的现象。此外仅轮B通过制动推动转向时,也会发生这种交替转向的现象。
柔性底盘前轮转向系统是一个多输入多输出的控制系统,其单轮驱动转向仿真试验说明,作为输出量的转向角之间存在耦合作用。该作用会给转向角的精确控制带来困难,但也使得各轮的转角不能偏离阿克曼转向角太多。
从图8还可以看到,在仿真转向过程中与转向结束后,轮A回正力矩是负值,其侧向力推动转向,但轮B回正力矩一直都是正值,其侧向力阻止转向,这意味着单轮驱动转向过程中存在内部耗损,是一种不协调的转向方式。
2.2 车速对前轮转向的影响
2.2.1双轮比例控制转向
为分析车速对转向的影响,对不同车速下相同目标转向角的转向进行仿真对比。为使转向角趋近并稳定于目标转向角,且便于分析转向过程,选择P(比例)控制对两前轮的驱动力矩进行控制。
仿真目标Ratt设定为7 m,根据式(22)、(23),轮A与轮B的目标转向角分别为8.94°、9.73°;车速分别设置为10、20、30、40 km/h;只对两前轮的驱动力矩进行比例控制;其余参数设置与单轮驱动仿真时相同。仿真结果如表2所示,表中的P(比例系数)综合考虑静差与稳定时间,通过反复调节得到。从表2可以看到,随着车速增加,最优P增加,但静差及转向稳定后的回正力矩却还是增加。其中初始车速为10、40 km/h的转向过程如图9所示,图9a表明,车速10 km/h时转向过程快速稳定且准确,车速40 km/h时,转向出现很大震荡,且轮B静差达到8.7%。仿真表明柔性底盘前轮转向系统具有较强的非线性。主要是因为随着车速增加,转向过程中两转向驱动单元受到的回正力矩急剧增加,并且车速40 km/h时,转向稳定后的回正力矩还保持较大值,驱动力矩也要较大才能与之平衡(图9b、9c)。
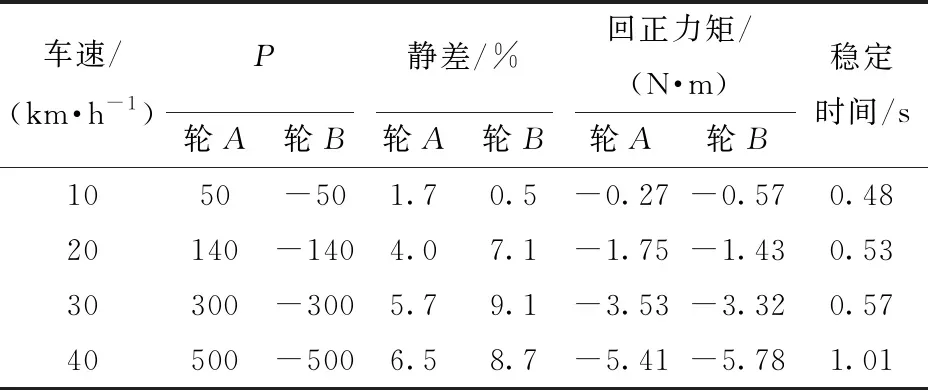
表2 不同车速下相同目标转向角的转向仿真结果Tab.2 Simulation results of the same target steering angle at different velocities

图9 相同目标转向角车速10、40 km/h时的转向仿真结果Fig.9 Steering simulation results at 10 km/h and 40 km/h of the same target steering angle
通过复杂的动力学方程组分析回正力矩急剧增加的原因比较困难,但可以对转向完成后的稳态状态进行近似分析。转向结束之后,转向角不变,底盘近似做匀速圆周运动;转向角较小,向心力近似等于4个车轮侧向力之和;车体转动角加速度为零,忽略较小的纵向力,则两前轮侧向力之和等于两后轮侧向力之和,因此可以得到轮胎侧向力近似公式为
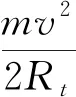
(24)
式中v——车轮质心速度,近似等于纵向车速
Rt——转向半径
根据式(11),式(24)可以变成
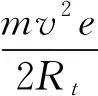
(25)
式(24)、(25)说明,转向稳定后的轮胎回正力矩由维持车辆转向的轮胎侧偏力导致,该回正力矩与整车质量、车速平方以及转向半径的倒数成正比。因此转向完成后两前轮回正力矩绝对值的和,在车速20、30、40 km/h时应该分别是10 km/h时的4、9、16倍。根据表2,实际分别为3.8、8.2、13.3倍。没有达到理论倍数是因为随着转速增加,实际转向角与目标转向角的静差变大。
可以将转向过程近似认为稳定转向状态的连续变化,因此转向过程中回正力矩也近似与车速的平方呈比例关系。轮胎纵向力力矩大于回正力矩才能推动转向,因此,转向过程中的驱动力矩也近似需要以与车速成平方的方式增加。
2.2.2单轮驱动转向
为分析车速对单轮驱动转向的影响,将初始车速分别设置为10、20、30、40 km/h,其余参数和控制量与2.1节相同,进行单轮驱动转向试验,结果如图10所示。由图10可知,同样的单轮恒定驱动力矩驱动转向,随着车速增加,转向角减小。这是由于同样转向角的回正力矩与车速平方成正比。车速增加后,该恒定驱动力矩只能与较小转向角的回正力矩平衡,即车速越大,稳定后的转向角越小。

图10 车速对单轮驱动转向影响的仿真结果Fig.10 Simulation results of influence of vehicle velocity on single-wheel drive steering
3 前轮转向试验
3.1 电子控制硬件与软件系统
电子控制硬件系统实物如图11a所示,原理图如图11b所示,原理图中只画出4组转向驱动单元中的一个。该电子控制硬件系统以主控制器为核心,它直接处理并识别遥控操纵信号与各轮转角、转速等传感器信号,输出PWM电压信号控制电动轮,并命令副控制器通过继电器控制电磁锁的开闭和电机的转动方向。主副控制器都采用STM32F103ZET6单片机。遥控手柄与信号接收器为富斯FS-i10型;转速传感器为杰特仕增量型光电旋转编码器(200P/R型);转角传感器为SAKAE公司22HP-10型精密多圈电位器(0~5 kΩ);电磁摩擦锁为KAIDE公司FBD050型;轮毂电机为富士达直流无刷轮毂电机(额定电压48 V,额定功率500 W);轮毂电机驱动控制器为芯动科技WX_WS4864型全智能无刷控制器,该控制器根据控制电压信号进行电机调速,根据开关信号控制电机转动方向。
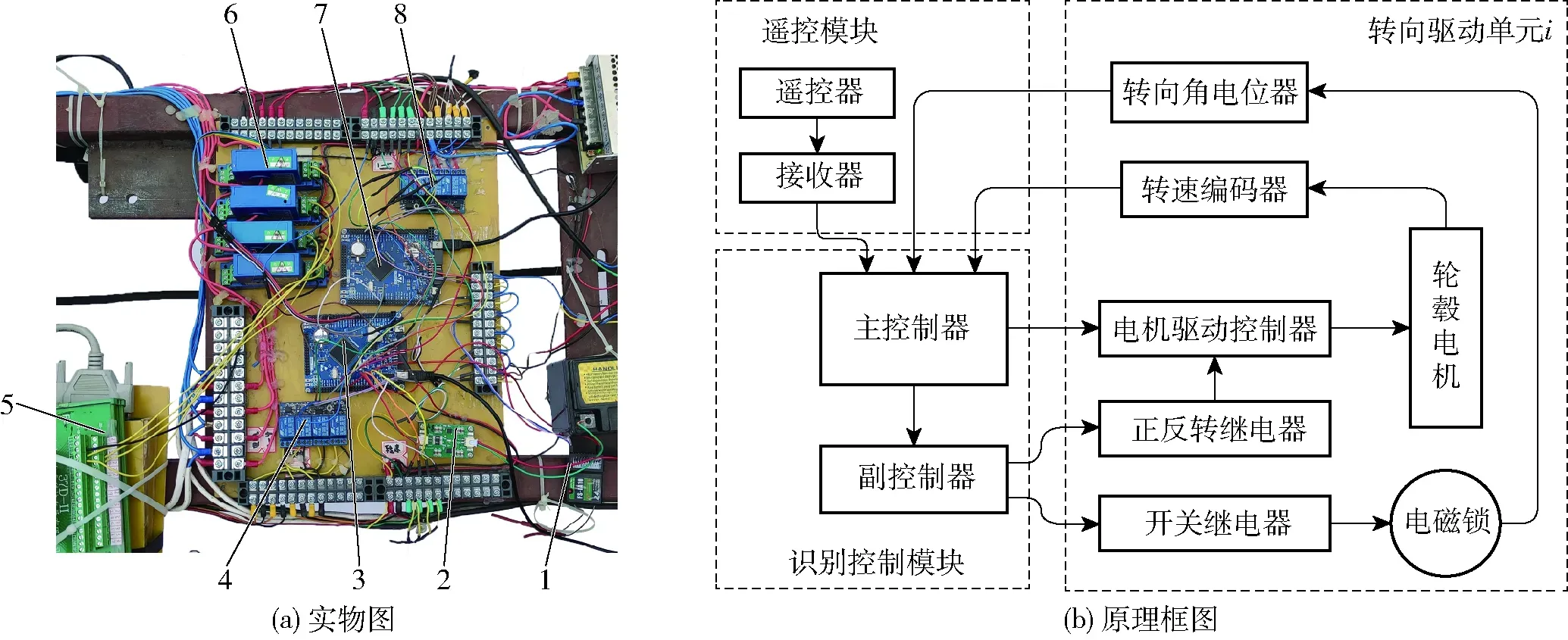
图11 柔性底盘电子控制硬件系统Fig.11 Hardware of flexible chassis electronic control system1.接收器 2.传感器用线性稳压降压模块 3.主控制器 4.电机转动方向控制继电器 5.采集卡 6.电流传感器 7.副控制器 8.电磁锁控制继电器
采用C语言在Keil uVision5环境下编写主、副控制器STM32F103ZET6单片机的控制软件。软件具有模块化、分层次的特点。对于操纵命令信号、传感器信号、控制输出及各种通信都建立对应的底层子程序进行识别与处理,主程序通过对底层子系统的调用实施控制。控制硬件系统与底层子程序具有通用性,通过改变主程序即可实现原地转向、前轮转向等各种运动模式的控制。
3.2 实车控制策略
轮毂电机驱动控制器根据输入的电压信号进行调速。通过电机台架试验发现,当控制电压信号不变时,随着车轮受到的转矩增加,转速降低;当转矩固定时,随着控制电压信号增加,转速增加。这与周勇等[25]的描述相似。
第2节分析表明,柔性底盘前轮转向过程中,要求外侧前轮驱动,内侧前轮一边向前滚动一边制动。但实际控制过程中,尚不能精确地控制刹车或电机能量回收的制动力矩。此外,车速越低,需要的转向力矩越小,因此当车速较低时,可以通过增加外侧车轮驱动力矩,而内侧车轮不驱动,靠滚动阻力带来的轮胎纵向力力矩与回正力矩推动转向的方式转向。
3.3 测试方法
各轮转角、转速、控制电压与电磁锁信号由主控制器发送到上位机,采集频率为20 Hz。轮毂电机母线电流通过华控兴业HKK-10I型直流电流变送器(量程0~20 A)测量,通过中泰研创USB7648B数据采集卡采集,采集频率10 000 Hz。
3.4 测试结果与分析
3.4.1最低车速转向试验
实车转向时目标近似转向半径Ratt=2 m,则右转向时,θrAt=-30.96°,θrBt=-24.53°。
调速PWM的高电平为3.3 V,占空比分辨率为0.1%,即平均电压的调节灵敏度为0.003 3 V。试验中发现,PWM占空比为48.7%,相应平均电压为1.607 V时车轮才开始转动,对应的车轮稳定转速为30.7 r/min,车速为0.69 m/s。在该最低车速时,通过测试发现,转向开始后两后轮保持PWM占空比不变,前轮电磁锁断电,外前轮PWM占空比增加2.8%,内前轮调速PWM占空比为零,可以实现近似半径2 m的转向。转向目标完成后电磁锁锁定,各轮PWM调速信号恢复直行时占空比。
实车转向过程如图12所示,实测结果如图13所示。图13a表明,初始车速为0.69 m/s时,通过增加外前轮驱动力矩,内侧车轮自由滚动,可以实现前轮转向,证明两轮之间存在较强的耦合关系。图13b、13c中,转向前与结束后虽然控制信号电压不变,但转速与电流发生变化,这是因为各轮转速由转向轮与瞬时转向中心的距离决定。图13a中,行进与转向过程中的各轮转角都出现较大跳动,可能是车体结构间隙引起的震动所致。

图12 实车转向过程Fig.12 Steering process of real vehicle

图13 实车转向试验测试结果Fig.13 Test results of steering
3.4.2仿真模型验证
为了对仿真模型进行验证,需要测得轮毂电机的驱动力矩。该值较难直接测量,可以通过台架测试轮毂电机输出转矩Md与转速n和母线电流I之间的关系,进行2阶多项式拟合得
Md=0.341+3.86I+6.28×10-4n-0.297I2-
2.26×10-3In-3.13×10-3n2
(26)
决定系数R2为0.992,均方根误差(RMSE)为0.339 N·m。测得转速与母线电流,即可求得驱动力矩。将式(26)引入仿真模型,反复调节断电后的前轮电磁锁最大摩擦力矩,当其值为0.84 N·m时,仿真转向结果与实测值最为接近。将转向开始作为0时刻,转向过程的仿真与实测结果如图14所示,两者趋近一致。证明仿真模型具有较高精度。
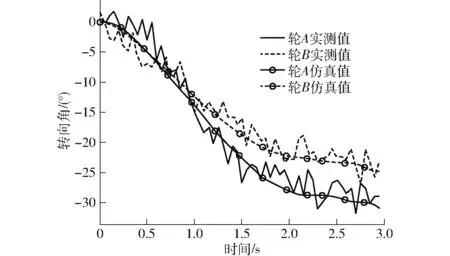
图14 转向过程仿真与实测结果对比Fig.14 Comparison of simulation and measured results of steering process
3.4.3不同车速转向试验
将PWM电压信号的占空比依次增加1.0个百分点,得到不同的车速,进行前轮转向试验。与最低车速转向试验相同,转向时外前轮调速PWM占空比增加2.8个百分点,内前轮占空比为零。与最低车速转向不同,车速增加后左右轮没有转到目标转向角,前轮电磁锁一直没有锁定。结果如表3所示,表中实车转向数据为5次重复试验的平均值。
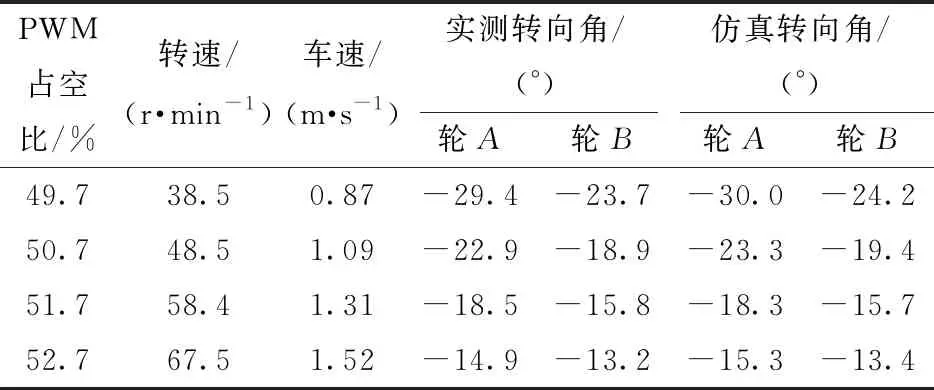
表3 不同车速下实车转向及其仿真结果Tab.3 Real vehicle steering and corresponding simulation results at different vehicle velocities
计算发现,转向过程中,各车速下驱动力矩的变化与最低车速时比较接近。但从表3可以看出,随着车速增加,最终转向角减小。证实了车速越高,转向过程中所需的车轮驱动力矩越大。
4 结论
(1)7自由度动力学仿真模型具有较高的准确度,可作为后续控制策略研究的虚拟仿真平台。
(2)柔性底盘前轮转向过程中,转向轮之间存在很强的耦合作用,耦合的关键因素是两转向轮转向角偏离阿克曼转向几何导致的轮胎回正力矩,该回正力矩阻止这种偏离,同时偏离程度越大,该回正力矩越大,反之亦然。
(3)柔性底盘前轮转向系统具有较强的非线性,造成非线性的主要原因是维持转向的轮胎侧偏力导致的轮胎回正力矩。转向稳定后,该回正力矩近似与整车质量、车速平方以及转向半径的倒数成正比。随着车速增加,转向角相同时,转向所需驱动力矩与速度的平方成正比。
(4)前轮转向过程中内侧车轮需要制动力矩,需进行结构或电机控制改进才能满足前轮转向的控制要求。
(5)柔性底盘前轮转向系统具有耦合性与非线性特点,因此经典的PID控制不适用,后续研究需要考虑通过滑膜控制等智能控制方法,实现不同车速、不同路面条件下的稳定与精确转向。
