不同形式锚泊系统对海洋资料浮标水动力性能的影响
2022-03-14路宽饶翔王花梅张倩
路宽, 饶翔, 王花梅, 张倩
(国家海洋技术中心, 天津 300112)
0 引言
海洋资料浮标是海洋环境长期、连续、实时监测的基本手段,是保障国家海洋安全、提高海洋科学研究水平、增强灾害预警能力的重要技术保障。从20世纪40年代末开始,国外就开始了海洋资料浮标的研发工作,美国国家资料浮标中心从创立开始至今,一直致力于浮标体、锚泊系统、传感器集成于通信等技术的研发工作。美国伍兹霍尔研究所作为海洋研究领域的领军者,也有着多年海洋浮标的研制经验。伴随着电子技术的进步,浮标的体积和质量不断减小,建造成本不断降低,而浮标测量及数据传输、可靠性的提高则加强了浮标连续工作的能力。浮标的研究重点也从优化结构转向优化浮标的内部系统。我国浮标研制工作起步于20世纪60年代,由单一参数测量浮标逐渐发展为多参数综合监测浮标,整体技术水平已接近世界先进水平,并拥有多种型号(直径分别为10 m、6 m、3 m、2.4 m和2 m等)和不同功能(水文气象监测、海洋动力环境监测、生态水质监测、应急核辐射监测等)的浮标,特别是10 m大型浮标和3 m小型浮标在国内海洋环境监测和海洋科学研究中发挥了重要的作用。
浮标在海上受到风、浪、流等作用时,不可避免地会发生摇荡,进而影响浮标上测量仪器设备的测量精度,同时在各种载荷作用下浮标会发生大范围位移,因此对其锚泊系统设计提出了更高要求。与其他海洋工程装备相比,浮标的锚泊系统所占比重较大,锚泊系统对标体的运动和受力影响较大,耦合效应明显,对其进行相关的水动力特性分析十分必要。因此,研究浮标及其锚泊系统的水动力特性,验证其能否在复杂海况下工作,提高观测要素的测量精度,一直是海洋资料浮标设计与研制的重点问题。
目前,对于浮标水动力特性研究的主要方法包括理论分析、数值模拟、物理模型试验和现场观测试验。其中理论分析需要建立理想的模型,对浮标系统进行各种简化处理,而浮标系统在海上风、浪、流等环境载荷作用下的运动与动力响应,属于一个较复杂的力学问题,因此理论分析的范围比较局限。现场观测试验虽然是海洋浮标最直接、准确的研究方法,但是试验成本较高。随着计算机技术及试验能力的提升,数值模拟与物理模型试验成为海洋浮标最主要的研究手段,在数值模拟方面,Fluent、AWQA、ADAMS、RecurDyn等数值模拟工具可很好地进行流体与固体耦合、多体动力学和锚泊系统的非线性等水动力学分析。在物理模型试验方面,多个大型多功能波浪水池的建立为浮标模型试验提供了完备的试验平台。尽管如此,我国对于海洋浮标系统的研究仍需要进一步深入,这是因为虽然我国浮标现场观测数据较为丰富,但对于数据准确性的验证手段仍需进一步提高。同时,我国采用数值模拟研究较多,而物理模型试验仍不够系统,二者之间的验证也不够充分。
本文针对威海海域水文情况,采用数值模拟与物理模型试验相结合的方法,对风浪作用下半拉紧式、倒s式和松弛式3种不同锚泊系统对海洋浮标水动力性能的影响进行研究与分析,所得研究结果对于国家海洋试验场海洋浮标的研制及其他浮标应用,具有重要参考意义。
1 威海海域情况与锚泊系统方案
山东威海北部褚岛海域,需要布置3 m多参数海洋综合浮标以长期、实时观测海域的水文气象等环境背景场情况,由于该海域需要建设国家海洋综合试验场,服务于我国海洋仪器设备科技创新、成果转化与业务化应用,对海域环境背景场数据的要求较高。该海域四季分明,与同纬度的内陆相比,具有雨水丰富、气温适中、气候温和的特点,属温带季风型气候。根据2008年威海气象台实测资料统计,全年平均风速4.1 m/s,全年各向风速大于5.4 m/s的概率为28.8%,风速大于8 m/s的概率为8.3%。2013年与2015年,国家海洋技术中心分别采用了松弛式与半拉紧的锚泊方式对海域进行了全年的波浪观测。其中2013年的观测数据按月份统计如表1所示。
锚泊系统的方案参照美国国家资料浮标中心规定,浮标锚泊系统根据布放水深不同,可以分为浅海 区、中等深度海区、深海区3种标准型式。在水深小于60 m浅海区,采用全锚链松弛式系留,锚泊系统深长比根据海流强弱来确定,一般为1∶3~1∶5;对于水深介于60~600 m中等深度海区,一般采用半拉紧式锚链与尼龙绳混合串接的系留方式,锚泊系统深长比为1∶0.9;水深600 m以上的海区,锚泊系统采用倒s式系统,采用锚链、浮球、聚丙烯缆等组成,深长比小于1∶1.25.考虑到由于该海域的水深约70 m,介于浅水与中等水深之间,因此有必要对风浪作用下,3个不同锚泊系统形式下的水动力性能进行研究与分析,以确定最佳方案。

表1 褚岛2013年实测波浪数据统计Tab.1 Measured wave data of Chu Island in 2013
2 数值模拟
2.1 模拟方法

图1 海洋资料浮标数值模型及网格划分Fig.1 Numerical model and mesh of ocean data buoy
海洋资料浮标的数值网格模型、网格划分及坐标系如图1所示,其中为模型坐标系,沿轴方向正向为风浪的进行方向。
利用ANSYS AQWA软件模块,对海洋资料浮标原型进行数值模拟计算,其主要环境参数与浮标原型尺寸如表2所示。

表2 主要环境参数与浮标原型尺寸Tab.2 Main enviromental parameters and buoy prototype sizes
对3种不同锚泊系统形式进行数值计算,其中,锚链的截面面积为0003 m,刚度为23×10N/m基于海上试验场当地水深为70 m,设置半拉紧式的锚链长度为72 m,悬链模型采用线性模型,单位宽度质量为5 kg/m;松弛式与倒s式的锚链长度取3倍水深,即210 m;悬链模型采用非线性模型,悬链微元420个,单位宽度质量为5 kg/m,其中浮力缆部分设为零浮力。
考虑到波浪对于浮标的作用力中流体黏性的影响相对较小,对运动和载荷的计算可以忽略,因此采用三维势流理论进行水动力计算,即假设流体是不可压缩、无黏性和无旋的。同时对时间项采用频域和时域两种计算方法,并考虑辐射阻尼的作用,对浮标水动力系数和运动响应进行数值计算分析。控制方程如(1)式所示:
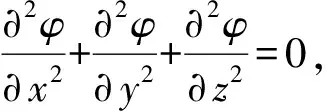
(1)
式中:为速度势,海表边界条件应满足:
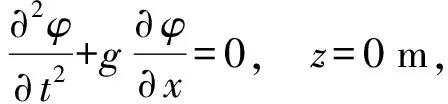
(2)
为重力加速度,海底边界条件应满足:
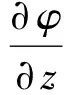
(3)
为水深。考虑静水回复力和波浪入射和绕射的作用下,1阶频域运动方程为
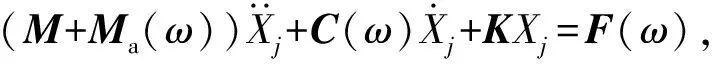
(4)
式中:为质量矩阵;为附加质量矩阵;为入射波频率;为浮标在6个自由度的位移,取1~6,分别对应纵荡、横荡、升沉、横摇、纵摇、艏摇;为辐射阻尼矩阵;为回复力矩阵;为1阶波浪力矩阵。
除了进行频域计算分析,还对浮标体在各种受力条件下时域运动状态进行计算,其中波浪荷载与风荷载是作用在浮标上的主要荷载。波浪荷载作用浮标时可利用莫里森公式计算:

(5)

风荷载主要作用在浮标水面以上的部分,以水平分量为主,垂直分量可忽略不计,其大小为
=0613,
(6)
式中:为风荷载;、分别表示浮标体受风构件的高度系数和形状系数,其中由于浮标在海面上高度低于153 m,故高度系数取10,形状系数中海面上浮标体部分取05,太阳能电池板取10,塔架杆件取13;为风速(m/s);为构件垂直于风向的正投影面积面积。
当风浪荷载耦合时产生了耦合运动,其时域耦合运动方程为

(7)
式中:、分别为线性和二次阻尼矩阵;为每个单元的矢量函数;为激振力矢量,主要包括风力、1阶波浪力、2阶波浪力和其他作用力等。
2.2 计算结果
采用频域计算模块对浮标的水动力性能进行了计算,浮标垂荡、纵摇的运动响应幅值算子(RAO)曲线分别如图2(a)、图2(b)所示。从垂荡RAO曲线可以看出:曲线逐渐接近于1,说明浮标在大周期的情况下随着波浪做等辐振动,随波性良好;波浪在常见波浪范围内,纵摇运动稳定且幅值较小,特别是长周期波浪纵摇非常小,浮标姿态比较稳定,纵摇固有周期为1.86 s.

图2 垂荡与纵摇RAOsFig.2 Heaving and pitching RAOs
采用时域模块,对风浪同时作用下3种不同锚泊系统的浮标姿态与锚链受力情况进行计算,重点比较横摇、纵摇与锚链拉力的情况,结果如图3~图5所示。从图3~图5中可以看出:半拉紧式的浮标横摇角与纵摇角最小,平均横摇角为0.8°,平均纵摇角为5.9°,倒s式的横摇角与纵摇角最大,平均横摇角为5.3°,平均纵摇角为6.3°,松弛式计算结果介于二者之间;倒s式锚链受拉力最小,平均值为550 N,半拉紧式锚链受拉力最大,平均值为2 360 N,前者是后者的23%.

图3 3种锚泊系统横摇对比Fig.3 Rolling comparison of three types of mooring systems
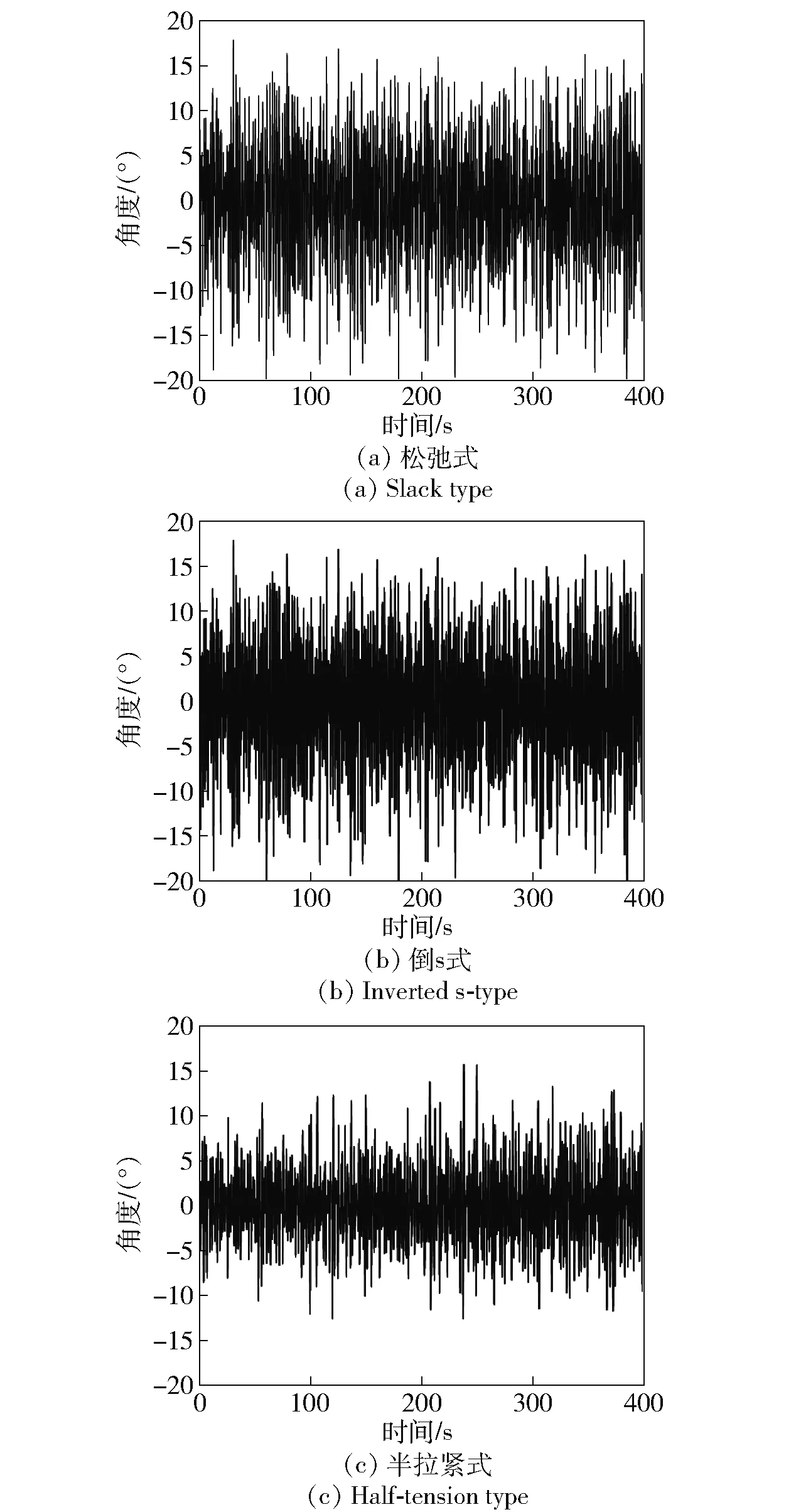
图4 3种锚泊系统纵摇对比Fig.4 Pitching comparison of three types of mooring systems

图5 3种锚泊系统拉力对比Fig.5 Tensile force comparison of three types of mooring systems
3 物理模型试验
3.1 试验系统及布局
试验在自然资源部国家海洋技术中心动力环境实验室中进行,本次海洋资料浮标的物理模型试验设施及设备包括:
1)多功能水池:长130 m,宽18 m,池深6 m,试验水深4.5 m.
2)造波机:自研制10单元伺服电机驱动式推板造波机,最大波高0.6 m,周期范围0.5~5.0 s,由上位机软件控制,可模拟产生规则波和不同谱型的不规则波。
3)造风系统:自研制,由16单元轴流风机组成,最大风速10 m/s.
4)双线性型BG-II波高传感器:量程0~1 m,精度0.2%.
5)Testo热敏风速仪405i:量程0~30 m/s,精度±0.1 m/s+测量值的5%。
6)DDEN水下拉力传感器:量程250 N,精度0.1%.
7)6自由度非接触姿态测量系统:自研制,三光学镜头组成,量程6 m×6 m,摇摆角误差±1.5°,水平位移误差1.5 mm,垂荡误差2 mm.
按照我国海洋行业标准HY/T 0299—2020 海洋观测仪器设备室内动力环境模型试验方法 总则规定进行试验布局。试验系统包括试验环境模拟装置、浮标模型与测量采集系统。其中,试验环境模拟装置包括造波机与造风机。前者为10单元伺服电机驱动式推板造波机,最大波高0.6 m,周期范围0.5~5.0 s,由上位机软件控制,可模拟产生规则波和不同谱型的不规则波,消波滩可消除90%的反射波。后者为16单元轴流风机组成的造风机,最大风速10 m/s,可由上位机软件控制不同的风速。浮标模型包括浮体及其锚泊系统,锚泊系统可进行更换。测量采集系统包括:波高仪、风速仪、6自由度姿态仪及拉力传感器。各测量传感器集成在数据采集系统中,保持数据的同步性。
浮标模型布放在距造波机30 m,距造风机20 m处,波高仪与风速仪布放在模型前5 m处,水下拉力传感器安装在模型与锚泊系统连接部位,6自由非接触姿态测量系统布置在模型背浪一侧的斜上方距离5 m附近,如图6所示。试验前需在模型上安装标志点,以满足测量需要。试验仪器均在计量有效期内,试验前也均进行了标定。

图6 试验布局Fig.6 Test layout
3.2 模型及相似准则
根据实验室试验能力与浮标原型尺寸,确定模型比尺为1∶5,设计时首先考虑满足几何相似,除几何相似外,浮标模型还满足了惯性矩和自摇周期相似,并且满足重力相似;其3种锚系结构的组成,除满足长度等几何相似外,还满足了质量和弹性相似。由于本次模型试验,水的黏滞力不是主要作用力,试验中并没有考虑雷诺数的影响。
试验前,首先进行压载调整,并通过调整压载分布调整质量、重心与转动惯量,使其达到目标值。模型考虑了上层结构及其搭载传感器等,以保证能够较合理的模拟原型的受风面积。模型主要参数如表3所示。

表3 模型主要参数Tab.3 Parameters of model
试验中采用3种锚系方案如图7所示,分别为松弛式、倒s式和半拉紧式。松弛式锚泊系统由锚链- 弹簧- 锚链组成,倒s式由锚链- 浮力缆- 普通缆- 锚链组成,半拉紧式由锚链- 普通缆- 锚链组成,锚块质量为20 kg,锚链质量与尺寸与原型保持相似。试验前对锚泊系统的水平刚度进行了验证。

图7 3种锚泊系统示意图(上)与模型(下)Fig.7 Sketch map (upper) and models (below) of three types of mooring systems
3.3 试验工况
威海海域四季分明,冬季受季风影响显著,风浪较大,春季季风转向,风浪逐渐减小,由于所在海域紧邻大陆,受夏季季风向影响的风浪无法成长,故夏季风浪较小。基于上述分析将海域海况按季节进行划分开展试验,同时对极值月(1月)作为单独工况进行试验,以验证其在恶劣海况下的水动力性能。原型实际海况如表4所示。
根据原型工作海况,按照缩尺比计算,得到试验工况如表5所示,3种锚泊系统方案、每组5个工况,共计15组工况。试验中,首先继续风场模拟,待风场稳定后,进行不规则波模拟。不规则波采用北海联合海浪计划谱,每组工况保证采集到波个数大于100.
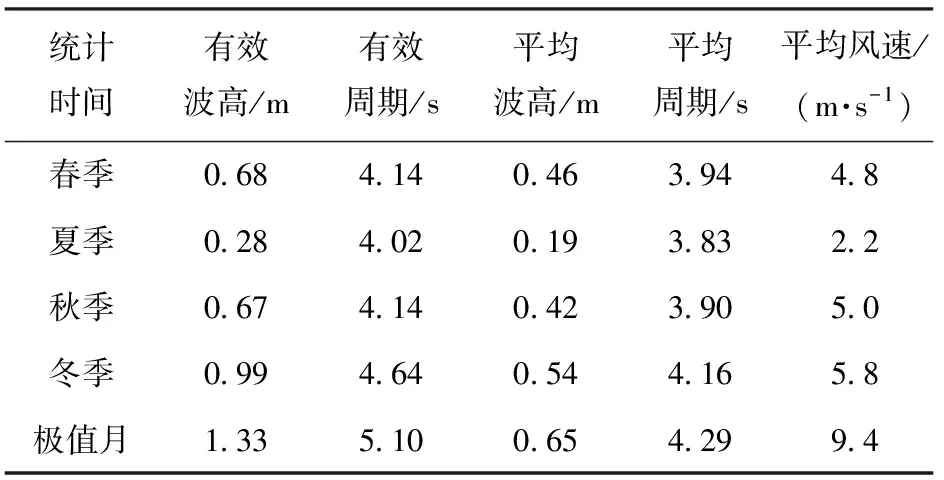
表4 原型实际海况Tab.4 Actual sea conditions of prototype
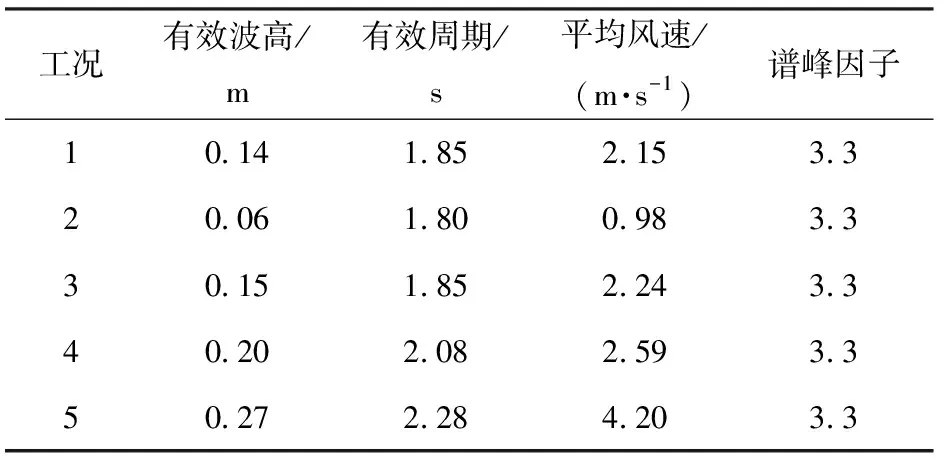
表5 模型试验工况Tab.5 Test conditions of model
3.4 试验过程与结果分析
采用最具代表性的极值月(工况5)试验结果,对3种锚泊系统下浮标模型的响应进行分析。首先,对于松弛式锚泊系统试验,结果如图8所示。由图8可见:锚链所受最大的瞬时拉力13.3 N(见图8(c));模型在原点0.2 m附近进行小幅度横荡运动(见图8(d));由于风的作用,模型首先产生了1.5 m的纵荡运动,当波浪作用于模型后,模型在1.0 m范围内进行较大范围的运动(见图8(e));模型的垂荡幅度与波幅相近,随波性良好;模型有较大的摇摆运动,最大纵摇角达到20°(见图8(h)),横摇运动不明显,维持在4°范围内(见图8(g));风的作用对初始艏摇角影响较大,稳定后,在风浪联合作用下,艏摇角维持在40°范围内(见图8(i))。

图8 松弛式锚泊系统模型试验结果Fig.8 Test results of slack type mooring system model
倒s式锚泊系统试验结果如图9所示。由图9可见:锚链所受最大的瞬时拉力仅为10 N(见图9(c));模型在原点1 m附近进行大幅度横荡运动(见图9(d));由于风的作用,模型首先产生了3 m左右的纵荡运动,当波浪作用于模型后,模型在1 m范围内进行较大范围的运动(见图9(e));模型的垂荡幅度同样与波幅相近,随波性良好;模型产生了显著的摇摆运动,最大横摇和纵摇角都达到了15°以上(见图9(g)与图9(h));艏摇角没有明显的稳定位置,在风浪联合作用下存在60°左右的运动范围(见图9(i))。
对于半拉紧式锚系试验,结果如图10所示。由图10可见:锚链所受最大瞬时拉力超过了80 N(见图10(c));浮标模型在较小的范围内做横荡与纵荡运动(见图10(d)与图10(e));模型的垂荡运动明显受到锚链拉力的影响,向水下方向的位移较大(见图10(f));模型的摇摆运动相对前两组的试验结果较小,其中横摇平均值为0.69°(见图10(g)),纵摇平均值为1.15°(见图10(h));风的作用对初始艏摇角影响较大,稳定后,在风浪联合作用下,艏摇角维持在20°范围内(见图10(i))。
将试验结果通过比尺换算,得到原型数据如表6所示。通过图3~图5与图8~图10对比来看,对于3种锚泊系统的定性结论是一致的:在松弛式、倒s式与半拉紧式3种锚泊系统方案中,采用半拉紧式锚泊系统,浮标模型的摇荡更小,可获取到更为准确的观测数据,但是锚链所受拉力最大;倒s式锚泊系统锚链所受拉力小、可靠性高,但是摇荡较大;松弛式锚泊系统的试验结果则介于半拉紧式和倒s式之间。如果定量来看,通过对比分析,数值计算与物理模型试验结果在拉力、横摇、纵摇有大约10%左右的偏差,造成偏差的原因有以下3个方面:1)计算软件的原因,ANSYS AQWA软件基于势流理论,在计算的过程中存在很多的假设;2)试验环境产生的误差,风场质量和反射波的影响都会对试验结果造成影响;3)试验过程中出现的不确定性因素,试验中,波高仪、风速仪、姿态仪、拉力计,都存在着系统误差,会对结果造成影响。
由表6可以看出:
1)倒s式锚泊系统的布放较方便,由于其系泊缆所受拉力较小,其抵抗极端环境的能力更强,维护周期更长。但其浮标在风浪作用下摇摆比较剧烈,因此观测数据的准确度会受到较大的影响,数据应采用相关算法进行修正后方可应用。
2)半拉紧式锚泊系统的定点观测效果最好,巡航半径较小,同时由于其在风浪作用下摇摆角更小,其内置的波浪传感器、搭载的风速传感器等获取的数据更为准确,但是其对锚泊系统要求较大,系泊缆所受瞬时拉力较大,长期使用会产生疲劳,应定期进行巡检和维护。
3)松弛式浮标工作姿态和锚泊系统可靠性介于半拉紧式和倒s式之间,在选择锚泊系统方式时,还应根据具体情况进行分析与判断。
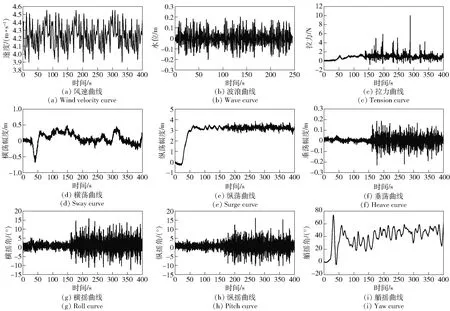
图9 倒s式锚泊系统模型试验结果Fig.9 Test results of inverted s-type mooring system model

表6 原型数据统计表

图10 半拉紧式锚泊系统模型试验结果Fig.10 Test results of half-tension type mooring system model
4 结论
本文采用数值模拟与物理模型试验研究的方法,针对3种典型不同锚泊系统方案,采用威海海域实测数据,对海洋浮标在风浪联合作用下的水动力性能进行研究与分析,通过试验不仅定性分析了不同方案的优缺点,而且得到了相对准确的定量分析结果,为今后类似研究提供了方法参考。得到如下主要结论:
1)在松弛式、倒s式与半拉紧式3种锚泊系统方案中,采用半拉紧的锚泊系统可获取到更为准确的观测数据,倒s式的锚泊系统可靠性则更高,松弛式的锚泊系统的性能则介于二者之间。
2)国家海洋综合试验场(威海)作为国家海洋仪器装备公共试验与测试平台,对海域背景数据的准确性要求较高。本文研究成果已应用在建立该试验场场区海洋环境背景场所需的浮标观测系统中,运行状态良好。
