大单元教学下正方体展开图的研究

杨霖锋

【摘  要】在小学数学教学中培养学生的空间建构能力十分重要，对正方体展开图的实践研究，能让学生从立体图向平面图的思维转化。基于此，本文就正方体展开图进行系统的分析和研究。

【关键词】展开图;空间模型;核心素养;大单元

在我国，发展学生的核心素养是在20世纪80年代提倡素质教育以及一些国家和组织研究核心素养的基础上提出来的，它可以使我国新时期的素质教育的目标更加清晰，内涵更加丰富，对基础教育课程改革和教学活动的开展更有指导性和可操作性。对中国学生核心素养的培养，将更加关注学生的自主学习;更加关注学生勇于探索、积极寻求有效解决问题的方法;更加关注学生的学习体验，注重对学生动手实践及创新意识的培养。

基于大单元教学的“项目性学习”，锻炼的是学生各方面的综合能力——质疑精神、严谨态度、合作能力、探究思想等。但它同时考验着学生的这些能力，考验着他们在这样的大环境下是否具备这样的能力发现问题，又能发挥每个人身上不同的能力合作解决问题？在这样的任务驱动下，又能否激发学生被隐藏的能力？实践出真知，实践一定会给予我们答案。更启发我们教师的是，在日常教学中，我们到底应该培养学生什么样的核心能力？我们到底应该如何改变自己的教育方式与理念？尤其小学数学教育，我们是否应该更多地放手，让学生自主探索？因为知识教给学生，一定比放在我们手上有更多的惊喜。下面结合正方体展开图的项目化教学对大单元教学进行探究。

一、问题缘起

人教版数学教材中在不同的学段体现对学生空间观念的培养，现结合正方体展开成平面图在一年级（下册）数学第一单元“认识图形（二）”（课本第7页第8题）和五年级（下册）第三单元“长方体和正方体”（课本第23页）的内容，分析在教学中教师的教和学生的学，发现未能达到新课程标准中对空间观念和几何直观两个方面的要求。表现为：教师在展开图的总结规律探究方面不充分，学生对正方体展开图空间模型的建构思维不足。

二、分析问题

1.正方体展开平面图是沿着某些棱剪开再展开的，空间思维无法建立，如何发展空间想象能力？

2.正方体展开图从几个层次和维度来研究？

三、研究方法

（一）实践探索建构模型法

1.实践操作

从正方体沿着某些棱剪开得到展开图是从三维空间逆向到二维平面的过程，很多学生在这一过程中不能建立思维模型，笔者认为不如以“怎样的平面图像能折叠成正方体”这一问题为切入点，这样就是由平面到立体过程，更容易使学生建构起空间模型。

准备工作：几十张完全一样的小正方形卡片（建议：边长为5cm的正方形，卡片用稍微硬一些的卡纸）;胶带（将正方形之间的边与边粘合）。

将每次实验成功的结果记录下来，共得到11种平面图形可以折叠成正方体。

2.分类整理

通过实验探索得到11种正方体展开图，并把它们进行分类，把这11种展开图分成四类：

3.建构模型

把这四类展开图进行模型化：

第一类属“141”模型：中间一行4个作侧面，上下一行各1个作上下底面。

第二类属“231”模型：中间3个作侧面。

第三类属“33”模型：两行只能有1个正方形相连。

第四类属“222”模型：每行之间只能有1个正方形相连。

4.口诀记忆

正方体展开图模型有11种，可分为4大类，4种模型，在记忆上很难记住每个模型的样子，所以提炼出一首口诀方便记忆。

口诀：正方体，也容易，平面展开别着急;

一四一，二三一，动一可得九变异;

两个三，中间串，制作飞件转得欢;

三个二，各错一，靠在墙边像楼梯;

旋转变换认真审，翻来覆去共十一。

（二）条件约束法

从11种正方體展开图中发现正方形的排列规律和约束条件：

1.行（列）数至多三行（列）;

2.最多的一行（列）正方形的个数至多4个且最多的一行（列）处于中间行（列）;

3.行与行之间只有一个正方形互相连接。

满足以上三个条件就一定能折叠成正方体。

（三）标数找对面法

正方体中若从一个面（a）只能有唯一一个对面（a′），从a面到a′面必须经过一个面，说明展开图后相对的两个正方形面之间必定隔了一个正方形，操作时将展开平面图的每个正方形标上1、2、3、4、5、6，观测哪两个数字之间隔了一个数字（说明这两个数字所在正方形是对面关系），若某个正方形不能直接观测出对面正方形，则需看上面、下面、左面、右面没有其他正方形，这个正方形便可向那个方向移动直至找到对面的正方形。如果一个面找到两个或者两个以上对面则产生矛盾，由于对面的唯一性，所以平面图不是正方体展开图，折叠不成正方体。

例1：

解析：

与数字3中间隔一个数字的有数字1和数字5，说明数字3的对面有两个正方形，这不符合正方体对面的唯一性，所以此图不能折叠成正方体，不是正方体展开图。

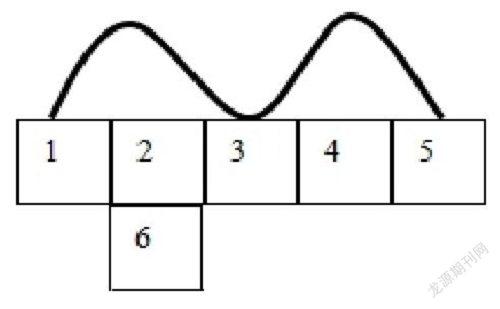
例2：

解析：

数字1的下方没有正方形阻挡着，故可以向下移动一格，则数字1和数学4中间隔了一个数字3，所以数字1和数字4是对面关系;

数字2的右方没有正方形阻挡着，故可以向右移动一格，则数字2和数学5中间隔了一个数字4，所以数字2和数字5是对面关系;

数字3的下方没有正方形阻挡着，故可以向下移动一格，则数字3和数学6中间隔了一个数字5，所以数字3和数字6是对面关系。

本文通过上述三种方法对正方体展开图进行了系统研究，教师把正方体展开图从三个维度去阐述给学生，有助于学生构建空间观念，培养学生在图形和几何方面的能力，教师应当将这种空间观念的培养贯穿数学教学的始终。

四、效果反馈

正方体的平面展开图种类繁多，形状各异。一个立体图形变换多种平面图形的问题，它实际上是一个立体图形转平面的问题，对学生来说有一定的难度，但它有一定的规律可循。可是若不能沿着一定的逻辑顺序去想、去记，就会显得繁琐、杂乱，无从下手。经过几年的教学尝试和实践，学生对正方体展开图的问题探讨和问题解决都有了新的高度。

总之，空间观念的培养是一个长期的过程，需要我们在平时的教学中持之以恒，遵循学生的年龄特点和认识规律，灵活运用课本资源，从低纬度到高规格地去探究规律方法，使学生在习得知识的同时，空间想象能力也得到有效提高。空间观念的建立是在关注学生数学学习结果的同时，更关注学生数学学习的过程，教师在其中扮演的角色也发生了很大变化，教师在教学过程中的作用应重新定位。

有问题，所以有思考;有思考，就有新方法。这样的大单元教学，就是一种新的教育方法，那么，未来的课堂定需要真正落实学生的全面发展，而不是让学生经不起磨炼;未来的教育方向定是培养学生的综合实践能力，而不只是“纸上谈兵”;未来的教师目标，定是让学生都爱上学习，让不同的学生得到不同的发展。