微穿孔板- 三聚氰胺吸音海绵- 空腔复合结构声学性能优化设计

王飞萌 王良模* 王 陶 王伟利 陈 威 姜统飞

(1.南京理工大学 机械工程学院， 南京 210094； 2.苏州江南航天机电工业有限公司， 苏州 215300)

引 言

微穿孔板是一种典型的共振吸声结构，最早由著名声学大师马大猷院士[1]在20世纪70年代提出。该结构在共振频段具有较好的吸声特性，在某些结构参数下甚至可以实现固定频率完美吸声，但是该结构的吸声带宽较窄且仅在低频段有效。

为了进一步拓展微穿孔板的吸声带宽，人们进行了大量研究。Herdtle等[2]研究了渐变形截面微孔的传递阻抗，将微孔切成厚度无限小且可以看作等截面的薄片，运用经典穿孔板理论进行积分，得到了锥形孔的声阻抗。马智慧[3]将突变型截面微孔等效为多个等截面微孔的串联并考虑权重因素，对每层穿孔板的声阻抗进行了修正。Ning等[4]对圆形孔、方形孔和三角孔的吸声性能进行了比较，结果表明，在截面面积相同的情况下三角孔的吸声性能最优，且在内切圆和外接圆半径不变的条件下，适当增加孔周长可以提升高频吸声效果和拓展吸声带宽。以上研究仅对孔形结构进行了简单的改变，很难获得理想的吸声带宽。

近年来，为了获得满意的吸声效果，人们研究了多种组合形式的微穿孔板结构以及微穿孔板- 吸声材料复合结构。田文昊等[5]采用传递函数法建立了双层串联微穿孔板吸声体的理论模型，分析了当两层微穿孔板参数及板后空腔改变时，结构整体吸音性能的变化。Cobo等[6]通过模拟退火算法优化了三层串联微穿孔板的参数，使其在某个规定的频带内具有最佳的吸声性能，并对单层和多层微穿孔板的理论模型和研究进展进行了综述。吴波波等[7]基于声电类比法研究了相同穿孔率、不等腔深的并联微穿孔板结构的吸声性能，发现吸声系数可以在3个倍频程范围内达到0.6以上。胡齐笑等[8]基于传递矩阵法研究了等腔深、不同穿孔率的并联微穿孔板结构的吸声特性，发现该结构比传统单层微穿孔板结构的吸声带宽大。刘志恩等[9]基于声电类比法研究了3种不同形式的混联复合微穿孔板结构(MPPAa、MPPAb、MPPAc)，结果表明这3种复合结构的吸声带宽均较大，优化后在500～3 600 Hz频段内MPPAc的平均吸声系数高达0.92。张丰辉等[10]基于传统的蜂窝夹层结构，在其内部引入波纹结构并且在面板和波纹上进行微穿孔，构成微穿孔蜂窝- 波纹复合结构，实现了优异的力学承载性能和低频段宽频吸声效果。Bravo等[11]研究了各向异性纤维材料支撑的微穿孔板的消声和吸声物理机制，为进一步进行参数或阻抗优化提供了指导。裴春明等[12]基于传递函数法研究了微穿孔板和吸声材料的几种组合方式，结果表明将吸声材料放置于穿孔板之前可以提高复合结构的吸声频带。尽管上述研究在拓展吸声结构的吸声带宽方面取得了一些进展，但仍存在一些不足：没有考虑实际应用中的安装空间，限制了其应用；在一定的约束条件下，对于一定的复合模型，获得最优参数的实用方法很少。

泡沫塑料等多孔材料用途广泛，可用于吸声结构[13-14]，可以通过改变工艺来控制多孔材料的孔隙率，从而有效调节其性能[15-17]。本文选用多孔材料三聚氰胺吸音海绵作为微穿孔板复合吸声结构的核心部分，在Johnson- Champoux- Allard(JCA)模型[18-19]和微穿孔板理论[1,20]的基础上，采用传递矩阵法建立了4种结构的吸声系数理论模型，研究了微穿孔板背腔中三聚氰胺吸音海绵的填充方式对吸声性能的影响；分析了微穿孔板的厚度、孔径、穿孔率及吸音海绵的厚度对微穿孔板- 三聚氰胺吸音海绵复合结构的吸声性能的影响；通过粒子群算法对其吸声系数进行了优化，并基于优化的微穿孔板参数研究了空气层厚度对微穿孔板- 三聚氰胺吸音海绵- 空腔复合结构的吸声性能的影响，最终得到综合性能较优的复合结构。

1 复合吸声结构的理论建模及仿真分析

1.1 复合结构

根据微穿孔板后三聚氰胺吸音海绵填充方式的不同，可以形成如图1所示的4种结构。图1(a)为微穿孔板- 空腔结构(结构a)，即微穿孔板背腔中没有填充三聚氰胺吸音海绵；图1(b)为微穿孔板- 三聚氰胺吸音海绵复合结构(复合结构b)，微穿孔板背腔中填满多孔材料；图1(c)为微穿孔板- 三聚氰胺吸音海绵- 空腔复合结构(复合结构c)，背腔中紧贴微穿孔板的一侧填充部分多孔材料；图1(d)为微穿孔板- 空腔- 三聚氰胺吸音海绵复合结构(复合结构d)，背腔中的多孔材料与微穿孔板被空气层隔开。

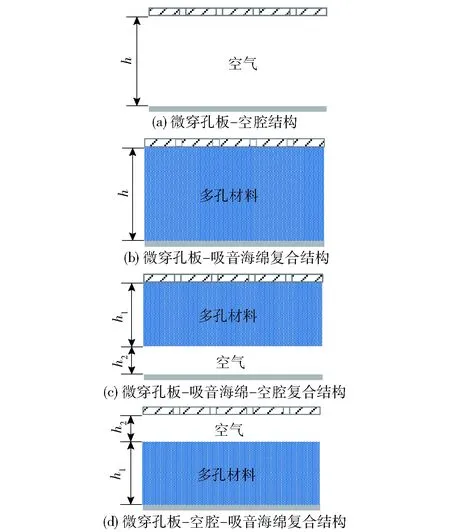
h为微穿孔板的背腔深度，mm；h1为多孔材料的厚度，mm；h2为空气层的厚度，mm。图1 不同多孔材料填充方式的吸声结构Fig.1 Sound-absorbing structures with different filling modes of porous materials

1.2 复合吸声结构理论建模

分别构建微穿孔板、空腔及三聚氰胺吸音海绵的传递矩阵，基于传递矩阵法建立图1中4种结构的吸声系数理论模型。

1.2.1微穿孔板的传递矩阵

微穿孔板的传递矩阵M可由式(1)求得。

(1)

式中，Zs为微穿孔板的声阻抗率，由实部R和虚部X组成，其公式如式(2)所示。其中，j为虚数单位，R和X可分别通过式(3)和式(4)计算。

Zs=R+jX

(2)

(3)

(4)

式中，μ为空气运动黏性系数，1.56×10-5m2/s；ρ为空气密度，1.21 kg/m3；t为微穿孔板的厚度，mm；p为微穿孔板的穿孔率；d为微穿孔板的孔径，mm；ω为角频率，ω=2πf(其中f为频率)；kr和km分别为声阻常数和声质量常数，其计算公式分别如式(5)和(6)所示。

(5)

(6)

(7)

式中k为微穿孔板常数。

1.2.2空腔的传递矩阵

空腔的传递矩阵C可由式(8)求得。

(8)

式中c为空气中的声速，340 m/s。

1.2.3多孔材料的传递矩阵

基于Johnson- Champoux- Allard等效流体模型[18-19]，三聚氰胺吸音海绵的传递矩阵P可由式(9)求得。

(9)

式中，kp为多孔材料中的波数，Zp为多孔材料的特性阻抗，其计算公式如式(10)和(11)所示。

(10)

(11)

式中，ρ(ω)为多孔材料的有效密度，可由公式(12)求得；K(ω)为多孔材料的有效体积模量，可通过公式(13)计算得到。

(12)

(13)

其中,

(14)

(15)

(16)

式中，α∞为曲折系数；σ为流阻；φ为多孔材料的孔隙率；γ为空气的比热比，1.40；P0为空气的静态压力，1.01×105Pa；B为空气的普朗特数，0.71；η为空气动力黏性系数，1.88×10-5m2/s；Λ和Λ′分别为黏性特征长度和热特征长度。三聚氰胺吸音海绵的相关参数见表1。

表1 三聚氰胺吸音海绵的参数

1.2.4复合结构吸声系数的理论模型

基于传递矩阵法将微穿孔板、空腔、多孔材料的传递矩阵按一定顺序相乘，可以得到全局的传递矩阵[21]。式(17)～(20)分别是图1中结构a～d的传递矩阵。

(17)

(18)

(19)

(20)

复合结构的表面声阻抗Zf为

(21)

反射系数β和吸声系数α分别为

(22)

α=1-|β|2

(23)

1.3 复合结构吸声性能分析及验证

为了分析多孔材料的填充方式对结构整体吸声性能的影响，设图1中4种结构的微穿孔板的几何参数为：孔径0.5 mm、板厚0.5 mm、穿孔率5%。结构a的空气层厚度为40 mm；结构b的多孔材料厚度为40 mm；结构c和d中空气层厚度为10 mm，多孔材料厚度为30 mm。设置计算频率为100～4 000 Hz，分别进行理论计算和有限元仿真。

图2是复合结构c的有限元模型图，该模型是使用COMSOL Multiphysics软件的压力声学模块搭建的。在该模型顶端设置完美匹配层边界来吸收由复合结构反射的平面波，其余边界设置为全反射边界。设置背景压力场以产生幅值为1 Pa的法向入射的平面波声场，使用内部穿孔板条件模拟微穿孔板结构，使用多孔介质声学中JCA模型模拟三聚氰胺吸音海绵，结构a、b和d的有限元模型可参考结构c搭建。

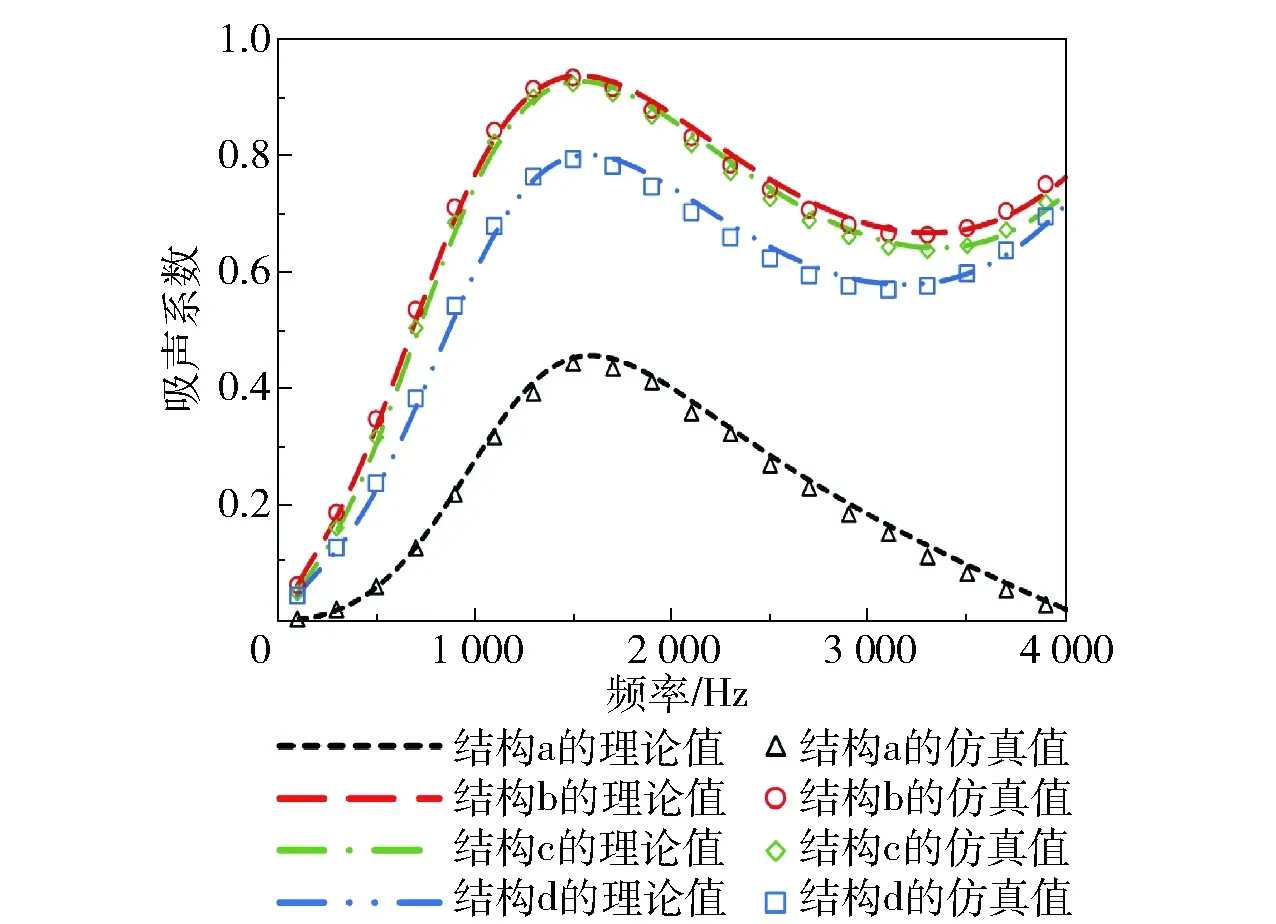
图3 4种结构的吸声系数- 频率响应曲线Fig.3 Sound absorption coefficient- frequency response curves of four structures

图3为4种结构的吸声系数的理论结果和有限元仿真结果。可以看出：(1)4种结构的吸声系数的理论值和有限元仿真的计算结果一致性较好，可以验证理论计算的正确性；(2)填充吸声材料三聚氰胺吸音海绵可以改善吸声效果。填满吸声材料的复合结构b具有最佳的吸声效果，填充部分吸声材料的复合结构d的吸声性能与复合结构b相比明显降低，填充部分吸声材料的复合结构c与复合结构b的吸声系数基本相同，因此下文针对复合结构b和c进行分析。

表2是4种结构的吸声系数共振频率、吸声系数峰值及吸声系数带宽。可以看出，4种结构的吸声系数共振频率相近，这是因为共振频率主要由微穿孔板的结构参数及背腔决定，三聚氰胺吸音海绵对共振频率的影响较小。在背腔中填充吸声材料时，吸声系数峰值和吸声系数带宽都比单纯微穿孔板结构大。这是因为吸声材料的填充将会改变背腔的声抗，主要等效为背腔深度的改变，因此在背腔中填充吸声材料可以在同等的空间内提高微穿孔板共振结构的吸声系数[22]。

表2 4种结构的吸声性能

2 几何参数对微穿孔板- 三聚氰胺吸音海绵复合结构吸声性能的影响

基于1.2节建立的理论模型，分析微穿孔板的孔径、厚度、穿孔率以及三聚氰胺吸音海绵厚度对复合结构b的吸声性能的影响。

2.1 微穿孔板孔径

为了分析微穿孔板孔径对复合结构b的吸声系数的影响，设定t=1 mm、p=5%、h=h1=30 mm保持不变，孔径d分别为0.5、1、1.5、2 mm，计算结果如图4所示。可以看出随着微穿孔板孔径的增大，复合结构b的吸声系数峰值逐渐降低，共振频率逐渐向低频方向移动并且吸声系数带宽也在逐渐变窄。在低频段，孔径对复合结构的吸声系数的影响很小并且吸声系数均低于基本吸声系数0.2；在中高频段，随着孔径的减小，吸声系数明显变大。

图4 不同微穿孔板孔径的复合结构b的吸声系数- 频率响应曲线Fig.4 Sound absorption coefficient- frequency response curves of the composite structure b with different apertures

图5 不同微穿孔板厚度的复合结构b的吸声系数- 频率响应曲线Fig.5 Sound absorption coefficient- frequency response curves of the composite structure b with different panel thicknesses

2.2 微穿孔板厚度

保持d=0.5 mm、p=5%、h=h1=30 mm不变，分别对微穿孔板厚度t为0.5、1、1.5、2 mm的复合结构b进行吸声系数计算，结果如图5所示。可以看出，随着微穿孔板厚度的增加，复合结构的吸声系数峰值明显增加，共振频率逐渐向低频方向移动并且吸声系数带宽逐渐变窄。在低频段，复合结构b的吸声系数随着微穿孔板厚度的增加而增加，吸声系数曲线的变化趋势逐渐变陡；在高频段，吸声系数随微穿孔板厚度的增大而大幅降低。

2.3 微穿孔板穿孔率

保持d=0.5 mm、t=1 mm、h=h1=30 mm不变，分别对微穿孔板穿孔率p为2%、4%、6%和8%的复合结构b进行吸声系数计算，结果如图6所示。可以看出，随着微穿孔板穿孔率的增加，复合结构的吸声系数峰值明显减小，共振频率逐渐向高频方向移动，吸声系数带宽得到了大幅度的增加。在低频段，随着穿孔率的增加，复合结构的吸声系数明显降低；在高频段，穿孔率的增加提高了吸声效果并且吸声系数曲线的变化趋势逐渐变缓。

图6 不同微穿孔板穿孔率的复合结构b的吸声系数- 频率响应曲线Fig.6 Sound absorption coefficient- frequency response curves of the composite structure b with different perforation rates

2.4 三聚氰胺吸音海绵厚度

保持d=0.5 mm、t=1 mm、p=5%不变，分别对多孔材料厚度h1为10、20、30、40 mm的复合结构b进行吸声系数计算，结果如图7所示。可以看出，随着多孔材料厚度的增加，复合结构的吸声系数峰值增加，共振频率逐渐向低频方向移动且吸声系数带宽也随之增加，这一特点在其他多孔材料如泡沫镍的研究中也有体现[23-24]。在低频段，随着多孔材料厚度的增加，复合结构的吸声系数明显提高，吸声系数曲线的变化趋势逐渐变陡；在高频段，复合结构b的吸声系数随着吸音材料厚度的减小而增大，但这只局限在一定频段内。实际上由曲线的变化趋势可知，多孔材料厚度的增加在总体上有利于提高复合结构的吸声效果。

图7 不同吸音材料厚度的复合结构b的吸声系数- 频率响应曲线Fig.7 Sound absorption coefficient- frequency response curves of composite structure b with different material thickness

3 基于粒子群算法的复合结构吸声性能优化设计

前文基于材料几何参数对复合结构b的吸声性能的影响因素进行分析，本节利用粒子群算法对某车载方舱内部复合结构的吸声性能进行优化设计。

3.1 粒子群算法

粒子群算法是由Kennedy等[25]提出的一种基于随机群体的优化算法。该算法的灵感来源于动物的集体行为，如鸟群的觅食行为。其基本思想是：在可行解空间随机生成一组粒子，每个粒子即为优化问题的一个可行解。通过定义适应度函数来衡量每个粒子的优越程度，每个粒子可获得各自的全局最优解gbest和局部最优解pbest，并通过式(24)和(25)在搜索空间移动以获得最优解。

(24)

(25)

(26)

式中，wmin和wmax分别表示最小和最大惯性权重系数，kmax表示最大迭代次数。本文取c1=c2=1.5，wmin=0.1，wmax=0.9。粒子群算法的实现步骤如下：

(1)初始化粒子群；

(2)建立适应度函数并计算每个粒子的适应度；

(3)比较每个粒子当前适应度值和个体历史最优适应度值，取最优值为pbest；

(4)比较每个粒子当前适应度值和群体历史最优适应度值，取最优值为gbest；

(5)根据式(24)和(25)更新每个粒子的位置和速度，其中w由式(26)得出；

(6)如果达到设定的迭代次数或者全局最优值已经收敛，则输出结果；否则返回步骤(2)。

3.2 微穿孔板- 三聚氰胺吸音海绵结构的优化

针对微穿孔板- 三聚氰胺吸音海绵复合结构b，采用粒子群优化算法优化其吸声性能。

(1)设计变量及优化目标 选取微穿孔板的孔径d、厚度t、穿孔率p以及吸声材料的厚度为设计变量，从提高复合结构全频段吸声性能的角度出发，取平均吸声系数αaverage为优化目标。所研究的复合结构主要有两个约束条件：(a)复合结构中多孔材料的厚度，这主要取决于安装空间，本文取40 mm；(b)微穿孔板的结构参数，这取决于设计要求和实际应用。由此，建立了单目标数学优化模型。

s.t.d∈[0.2 mm，2 mm]

t∈[0.1 mm，2 mm]

p∈[0，10%]

h1∈[0 mm，40 mm]

(27)

式中，f1为计算下限频率，Hz；f2为计算上限频率，Hz；α(f)为复合结构的吸声系数- 频率响应曲线。

(2)粒子群优化结果 基于粒子群优化算法对上述优化模型进行求解，设定迭代次数为100，种群中的粒子数为100。最终得到的微穿孔板参数为：孔径0.2 mm、厚度0.6 mm、穿孔率10%，三聚氰胺吸音海绵厚度40 mm，复合结构的平均吸声系数为0.765 3。

3.3 微穿孔板- 三聚氰胺吸音海绵- 空腔复合结构的优化

由1.3节的分析可知，复合结构c和复合结构b的吸声性能几乎相同，但复合结构c可以减少部分吸声材料，这样在保持吸声性能的同时实现轻量化。

3.3.1空气层厚度优化

采用上述粒子群算法优化得到的微穿孔板结构参数，分析复合结构c中不同空气层厚度对平均吸声系数的影响，结果如图8所示。可以看出随着空气层厚度的增加，平均吸声系数逐渐减小且下降曲线越来越陡。为了兼顾吸声效果和轻量化，选取平均吸声系数大于0.74且空气层厚度尽量大的结构作为最终设计方案，即空气层厚度为12 mm的复合结构c。

图8 复合结构c中空气层厚度对平均吸声系数的影响Fig.8 Influence of air layer thickness in the composite structure c on the average sound absorption coefficient

3.3.2优化方案对比

表3为优化前后复合结构的平均吸声系数，图9为优化前后复合结构的吸声系数- 频率响应曲线。为了体现三聚氰胺吸音海绵在复合结构中的吸声效果，将优化后复合结构b中的多孔材料层替换成空气层，形成结构a。由结果可以看出：与结构a相比，优化后复合结构c的平均吸声系数提升了0.380 4；与优化前的复合结构b相比，优化后的复合结构c不仅吸声峰值有所增加，而且平均吸声系数从0.565 4提升到0.751 9，在全频段都有良好的吸声效果；与优化后的复合结构b相比，优化后的复合结构c的平均吸声系数仅降低了0.013 4，但吸声材料厚度减少了30%。

表3 优化前后复合结构的平均吸声系数

图9 优化前后复合结构的吸声系数- 频率响应曲线Fig.9 Sound absorption coefficient- frequency response curves of the composite structure before and after optimization

4 结论

(1)与不填充三聚氰胺吸音海绵的单层微穿孔板结构a相比，填充吸音海绵可以改善复合结构的吸声效果；吸音海绵的填充方式对复合结构的吸声效果有影响：微穿孔板- 吸音海绵- 空腔复合结构c比微穿孔板- 空腔- 吸音海绵复合结构d的吸声性能好，与填满吸音海绵的微穿孔板- 吸音海绵复合结构b的吸声性能基本相同。

(2)对于复合结构b：微穿孔板的孔径越小，复合结构在中高频段的吸声效果越好；微穿孔板的厚度越大，复合结构在高频段的吸声性能越低；穿孔率越大，复合结构在低频段的吸声性能越低；吸音海绵厚度的增加在总体上有利于提高复合结构的吸声效果。

(3)经粒子群算法优化后的复合结构c与优化前的复合结构b相比，其平均吸声系数从0.565 4提升至0.751 9；与优化后的复合结构b相比，其吸声性能几乎不变，但吸声材料厚度减少了30%，在保持良好吸声性能的同时实现了轻量化。