循环射流混合槽内油- 水两相流复杂动力学特性分析

禹言芳 孔令敏 刘振江 陈雅鑫 孟辉波 吴剑华

(沈阳化工大学 辽宁省高效化工混合技术重点实验室， 沈阳 110142)

引 言

化学工业是国民经济的支柱产业，在由原来的高污染、高能耗、高排放的发展方式向节能减排降耗和可持续发展转型的升级过程中面临巨大压力[1]。化工过程强化在降低能耗、提高生产效率、减少污染等方面发挥着重要作用，因此成为人们关注的热点[2]。

射流混合器作为一种化工过程强化操作单元，因其结构简单、零部件不易损坏等优点而得到广泛应用[3-4]。针对射流混合器的研究最初由Fossett等[5]提出，他们分析了单孔倾斜侧面射流的圆柱形罐内四乙基铅与汽油的两相流动特性，总结了几种典型射流混合器内的混合时间关联式。Zughbi等[6]利用实验和数值模拟方法对射流搅拌槽内不同位置分布的射流进行研究，发现非对称射流比对称射流的混合效果更好。到目前为止，与射流混合相关的研究已经涉及到多相流混合领域，包括气固混合、液液混合、气液混合等。蓝敏乐等[7]对管内管型混合澄清槽内的液- 液两相流进行数值计算，发现降低分散相含量和进料油水比能够提高混合性能。黎义斌等[8]利用数值模拟的方法研究了直叶片与推进叶片对搅拌釜内流动结构及气液两相混合性能的影响，发现直叶片可以提高釜内涡耗散速度，缩短涡从产生到消失的周期。

化工设备混合效率多与内部流场的涡结构、涡强度及涡分布状态有关。Meftah等[9]研究了密集圆形射流孔垂直浸没射流时的混合过程，测量得到的流场证实了射流截面内上升和下降阶段反向旋转涡对的形成。Helmholtz[10]提出了涡丝的概念，将涡量Ω定义为涡的强度，对流动中的涡进行描述，被称为第一代涡。随着研究的不断发展，先后有学者提出以Q判据[11]、λ方法[12]、Δ判据[13]和λci判据[14]为代表的第二代涡判别方法，此类变量基本都是由速度梯度矩阵的特征值唯一确定，对流动状态中涡结构的识别能力更强。但是该类方法本身没有清晰的物理意义，对涡强度的判别模糊，其阈值判断法也容易过滤掉细小的涡结构。刘超群课题组[15-17]针对第二代涡判别方法存在的缺陷提出了第三代涡系列判别方法即Liutex判别法，对流体动力学的发展产生了一定程度的影响。

本课题组前期设计了利用多级离心泵驱动流体来实现流体的流动与混合的新型循环射流混合槽(CJT)[18]，对循环射流混合槽的射流孔和降液管形状等几何参数进行研究，发现射流孔形状为三角形时以及降液管为对称矩形时的流动特性较好[19-20]；通过实验与数值模拟的方法对槽内各个位置处的压力波动进行分析，并描述了流场内部的流动特性，发现循环射流混合槽脉动序列具有相关性和非周期性，且瞬态流动具有复杂的动力学特性及湍流特性[21-23]。

到目前为止，关于循环射流混合槽的研究主要集中在单相流流动特性及结构优化等方面，对槽内的液液两相流流动特性及其瞬态涡结构的演化分析较少。本文选取水和二甲基硅油(C6H18OSi2)作为介质，采用Eulerian- Eulerian方法对CJT内两相流流动进行建模；在Re=3 173～12 962和相含率αd=1.80%～6.00%条件下对水相的射流孔速度自相似性、平均涡量分布以及剪切速率等参数进行分析，并对Ω、Q与Liutex这3种涡结构判别方法进行比较。

1 数值模型

1.1 物理模型

循环射流混合槽内部结构较为复杂，由含有动量源的4根提升管和1根中心降液管组成，导流板在提升管与降液管之间将流场分为两个区域，含有提升管的区域为射流混合区，含有降液管的区域为中心混合区。为提高循环射流混合槽混合与搅拌的均匀性，4根提升管上沿轴向均匀分布9个射流孔，从下到上依次为jet1～jet9，其结构见图1。降液管出口尺寸、射流孔直径和导流板长度等参数见表1。

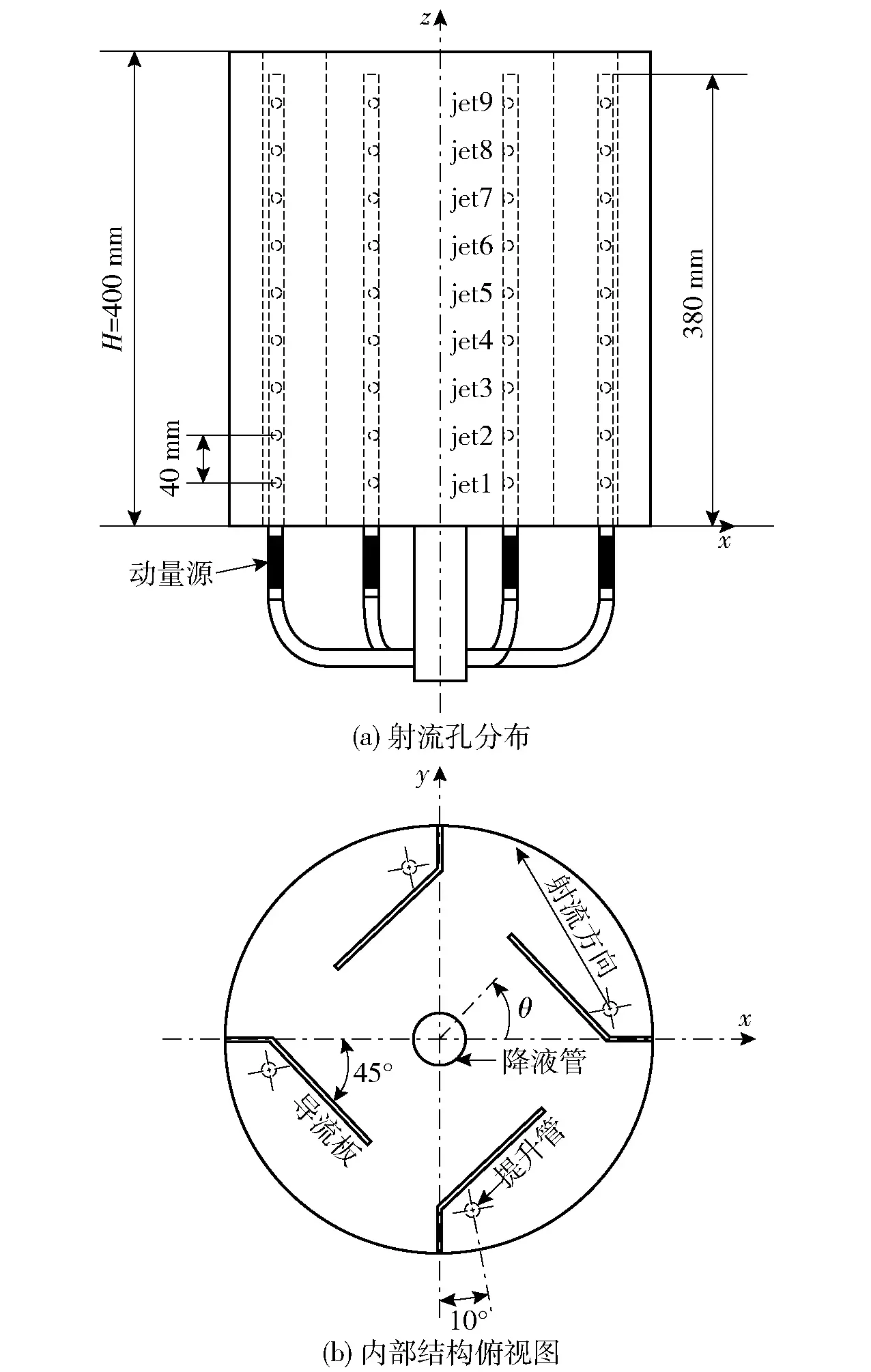
图1 循环射流混合槽几何结构模型Fig.1 Geometric structure model of the circulating jet mixing tank

在动量源的作用下，流体通过提升管的射流孔高速喷射进入槽体内部，与周围低速流体相互掺混，再经降液管到达动量源形成循环回路。流动工质为油- 水两相，其中连续相为水，分散相为二甲基硅油，其相关物性参数见表2。

表1 循环射流混合槽结构参数

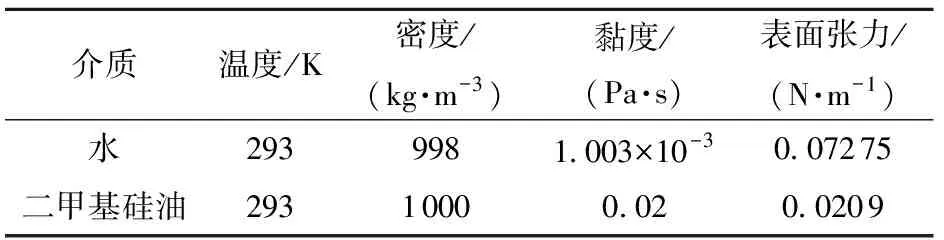
表2 介质物性参数

1.2 数值模型

采用有限体积法软件ANSYS FLUENT V16.1进行三维非定常不可压缩Navier- Stokes(N- S)方程的求解；多相流模型选取Eulerian- Eulerian模型[24]。Hosseini等[25]认为剪切应力输运(SST)k-ω湍流模型能很好地描述强剪切流体的流动状态，本课题组在前期工作中也发现该湍流模型能更好地预测CJT内的流动状态并准确捕捉流场信息[19,21]，因此本文选取SSTk-ω湍流模型对油水两相的流动混合特性进行模拟。

连续性方程为

(1)

动量方程为

(2)

式中，ρm为第m相密度，其中m=1、2，1表示连续相水，2表示分散相二甲基硅油；vm为第m相速度矢量；g为重力加速度矢量；p为压力；F为相界面合力，包括曳力、升力、湍流分散力、虚拟质量力及壁面润滑力，由于曳力的量级通常为其余作用力的100倍以上[26]，故本文只考虑曳力作用。

曳力Fdrag的表达式为

(3)

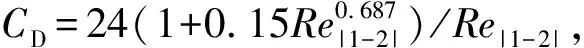
湍动能k方程和湍流耗散率ω方程分别为

(4)

(5)

式中，μm为第m相流体黏度；σk为湍动能普朗特数；σω为湍流耗散率普朗特数；μt为湍流黏度；Gk为湍动能的产生项；Gω为湍流耗散率的产生项；Sk为湍动能的源项；Sω为湍流耗散率的源项；Yk为湍动能的耗散率；Yω为湍流引起的ω的耗散；Dω为交叉扩散项。

1.3 边界条件

循环射流混合槽壁面采用无滑移边界条件，在提升管下部加入4个动量源来实现循环射流。采用求解压力耦合方程的半隐方法进行数值计算，动量、湍动能和耗散率方程均采用二阶迎风格式，梯度插值方案采用基于单元体的最小二乘法插值。以水为工质，在动量源体积流量Qv为1～4 m3/h (Re=3 173～12 692)的条件下进行稳态计算，Re的计算公式为[19]

(6)

式中，dj为特征直径即射流喷嘴的直径；v1为特征速度，其计算公式为

(7)

式中，N0为射流喷嘴的数量。

当内部流场达到稳定循环后，利用FLUENT中的patch功能在循环射流混合槽顶部添加不同体积的二甲基硅油(相含率αd分别为1.80%、2.86%和6.00%)，再进行油- 水两相非稳态流场计算。收敛极限均低于10-4，时间步长为0.005 s，在Re=3 173、6 346、9 519、12 692的条件下，库朗数(Courant)分别为0.168、0.342、0.506、0.682，满足库朗数小于1的要求[28]。

1.4 网格策略

利用ICEM软件通过两种方案对循环射流混合槽进行网格划分：方案一采用六面体结构化网格对整体进行划分；方案二对中心混合区采用多面体非结构化网格进行划分，射流混合区域仍然使用六面体结构化网格划分。基于方案二的轴截面混合网格示意图如图2所示。

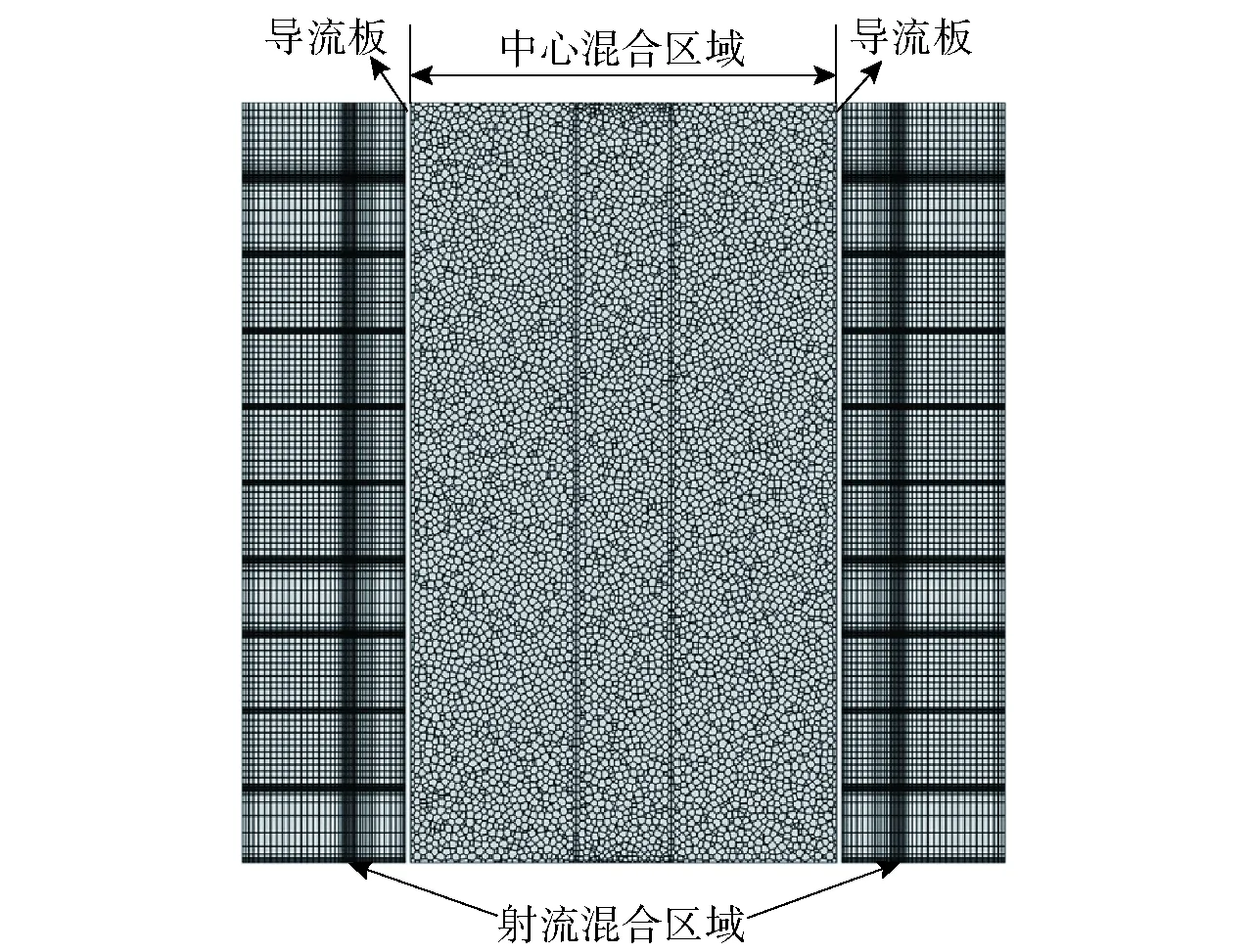
图2 循环射流混合槽内部截面网格Fig.2 Internal cross-section grid of the circulating jet mixing tank

1.5 模型有效性与网格无关性验证

以本课题组前期的压力波动实验结果[21]为依据，通过SSTk-ω湍流模型对两种网格进行数值计算，并将计算结果与实验值对比。图3为模型有效性验证对比结果，其中横坐标z/H表示无量纲高度。可以发现两种网格方案利用SSTk-ω湍流模型计算得到的数值结果与实验结果的误差范围均小于10%。其中，方案一的误差范围为4.95%～9.42%，方案二的误差范围为2.01%～7.48%，故选择方案二的网格划分方法进行数值模拟计算。

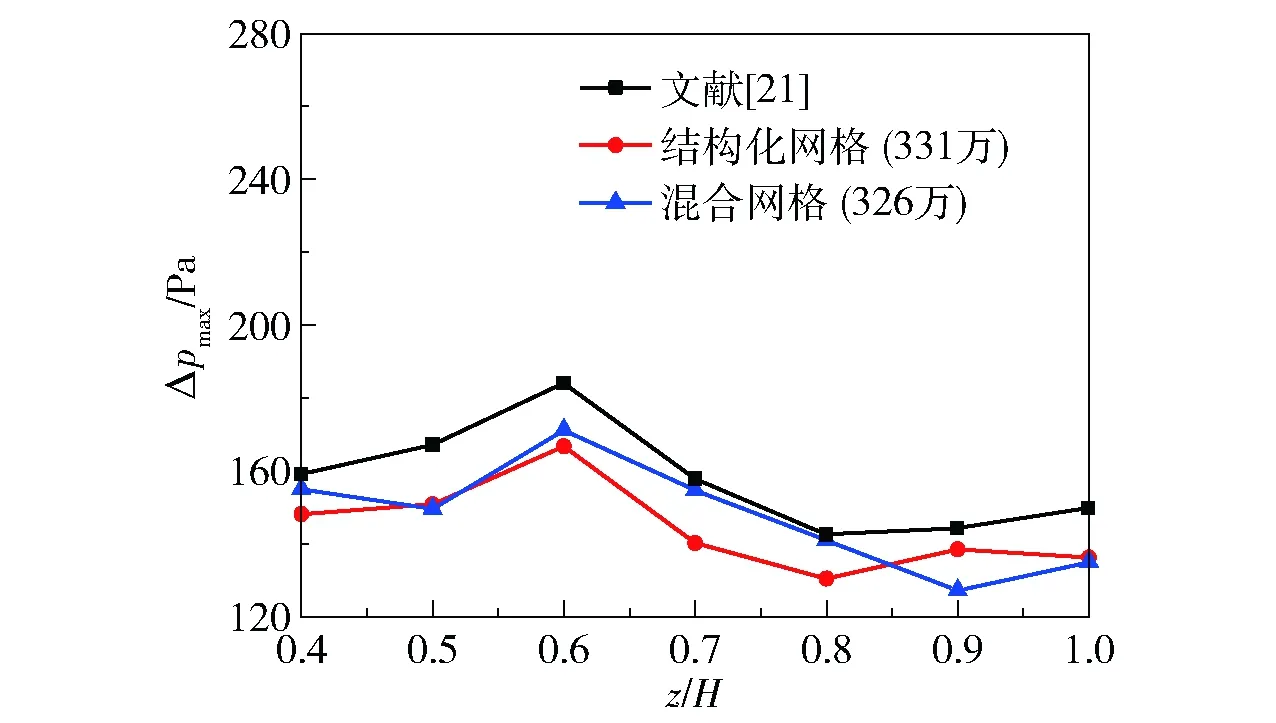
图3 数值模型有效性验证Fig.3 Validation of the numerical model

在Re=6 346的条件下，选择网格数量分别为160万、247万、326万、401万和460万的5种网格模型进行计算。前期研究工作表明，在数量为160万、247万、326万、401万的网格模型中，z/H=0.7处连续相在射流中心线上的速度与460万网格模型的预测结果相比，偏差分别为27%、26%、4.2%及4.8%，网格数量为326万时的偏差值最小(4.2%)[23]。综合考虑计算精度与计算效率两个因素，最终选取非结构网格数量为44.6万、结构化网格数量为281.4万即总数量为326万的混合网格模型对循环射流混合槽内油- 水两相进行数值计算。

2 结果与讨论

2.1 射流速度自相似性

对循环射流槽内流体的流动特性进行分析，考虑到9个射流孔的对称性，选取jet4、jet5和jet6进行研究。图4为射流方向无量纲速度的自相似性分布，其中l为射流中心线上某点到射流孔的长度，s为射流孔沿射流中心线到槽体壁面的长度，Um为水连续相在射流中心线方向上的合速度，U0为射流出口位置水连续相的初始速度，Um/U0为无量纲速度，H为循环射流混合槽高度。

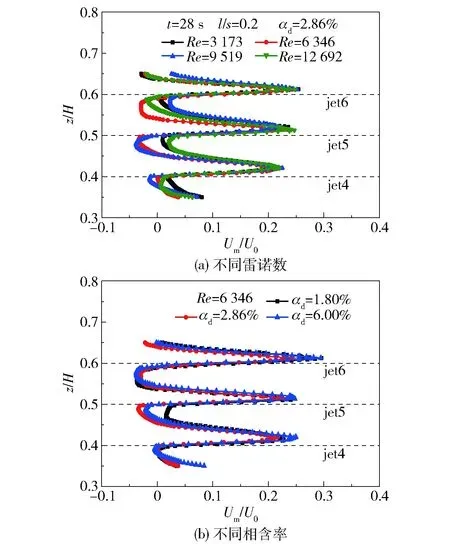
图4 射流方向无量纲速度的自相似性分布Fig.4 Self-similarity distribution of the dimensionless velocity in the jet direction

图4(a)为当t=28 s、l/s=0.2和αd=2.86%时，不同雷诺数条件下的射流自相似性。可以看出jet4、jet5和jet6的无量纲射流中心线速度具有较好的自相似性，受升力及多股射流间的卷吸作用，射流中心线均向上偏移，在z/H=0.45～0.5及z/H=0.55～0.6位置处出现回流，形成强制涡。在前期的研究工作中已比较过不同Re与不同相含率条件下两股射流间强制涡的湍动能，发现相含率对湍动能分布的影响较小，而雷诺数对湍动能的影响较大[23]：随雷诺数增加涡的湍动能会急剧增大，Re=6 346、9 519、12 692时强制涡的湍动能比Re=3 173时增加了10.6倍、16.4倍和32.8倍。

图4(b)为不同相含率条件下无量纲射流中心线速度的自相似性，其变化趋势与不同雷诺数条件下无量纲射流中心线速度的变化趋势相似，相比之下不同相含率条件下的自相似性更好。

2.2 涡结构判别方法比较

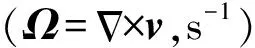
用平均涡量〈Ω〉对循环射流混合槽内流场轴向位置、径向位置和周向位置的涡量变化进行分析。平均涡量计算公式如式(8)所示[21]。

(8)

平均涡量〈Ω〉的正负可以表示涡量的主体方向：〈Ω〉为正，主体涡为正向涡；〈Ω〉为负，主体涡为反向涡。i、j分别为x、y方向上的离散点个数；Ωi,j为x，y方向上的涡量。

图6为〈Ω〉在轴向、径向、周向3个方向上的空间分布特性。图6(a)为不同轴向位置截面的平均涡量，整体上〈Ω〉大部分为正值，说明流场区域内流体正向涡占主导地位。在z/H=0.1即jet1附近，受槽体底部浮升力及周围射流卷吸的影响反向涡占主导地位，〈Ω〉出现负值。随着Re的增加，〈Ω〉值不断增大。z/H=0.9处，Re=6 346、9 519和12 692时的〈Ω〉比Re=3 173时的分别增大了118.3%、253.7%和373.4%。图6(b)为不同径向位置截面的平均涡量。由于受高速射流的影响，射流两边出现反向对涡(CVP)，故r/R=0.82附近〈Ω〉出现峰值，且峰值方向相反。在r/R=0.81处，与Re=3 173时的〈Ω〉相比，Re=6 346、9 519和12 692时的〈Ω〉分别增大101.7%、204.6%和306.4%。

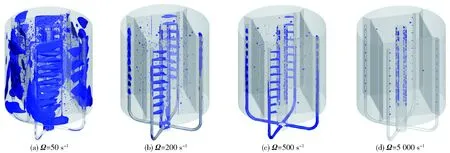
图5 Re=6 346下CJT内的涡量等值面Fig.5 Vorticity isosurfaces in Re=6 346

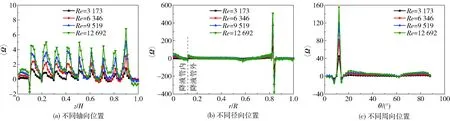
图6 αd=2.86%和t=28 s时不同位置处的〈Ω〉空间分布特性Fig.6 The spatial distribution characteristics of 〈Ω〉 at different locations when αd=2.86% and t=28 s

图6(c)为不同周向位置截面的平均涡量。受到射流初始速度影响在θ=12°即射流出口位置附近〈Ω〉出现峰值，与Re=3 173时相比Re=6 346、9 519和12 692时的〈Ω〉值分别增大81.3%、163.7%和243.8%。

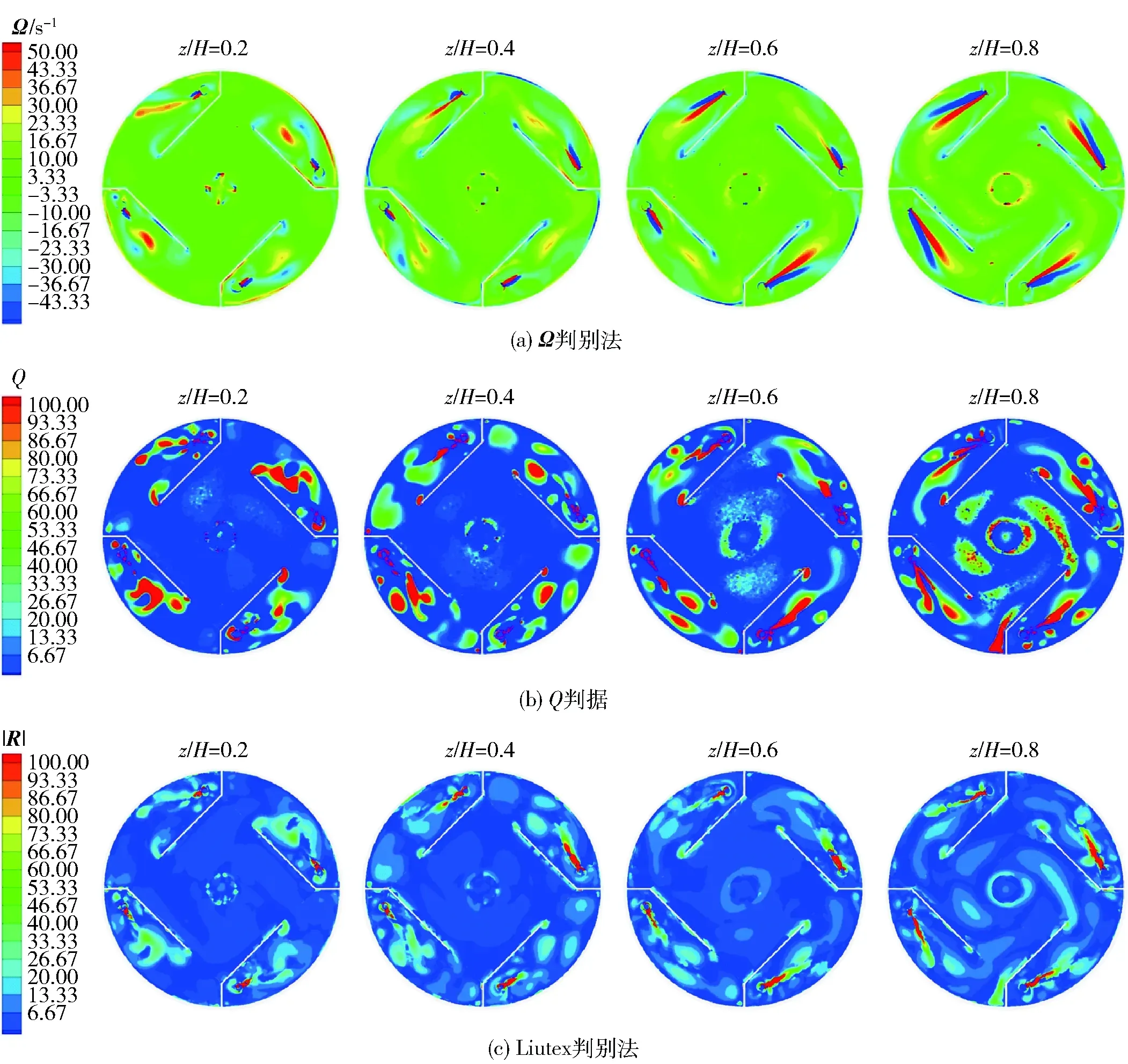
图7 不同轴向位置处3种涡结构判别方法的比较Fig.7 Comparison of three vortex structure identification methods at different axial positions

图7为不同轴向位置处涡结构的3种判别方式比较，即基于涡量计算的第一代涡判别法Ω、关注超出应变率大小涡量的第二代涡判别法—Q判据与考虑流场中当地流体运动的刚性转动部分的第三代Liutex判别法。可以看出，这3种判别法均能清晰地揭示CJT内射流中心线两侧的反向对涡以及导流板与降液管位置处的大尺度涡结构；在中心主体混合区域涡量存在，但部分涡结构不存在，说明Ω判别法认为涡量存在等同于涡存在的理论与实际有偏差；Q判据基于第一代涡判别法进行优化，明确了射流区域及中心主体混合区域的涡结构，但由于旋转和剪切的抵消作用对细小涡结构的判别易出现误差；Liutex在较大涡结构的判断中与Q判据相似，但在较小涡结构的判断中存在差别，如在主体流动区域降液管附近位置和导流板两侧，Liutex判别法更容易识别较小的涡结构。由此表明，Liutex涡结构判别与前两代涡结构的判别方法相比有较大改善，对于流场中涡结构的判断更加准确和细致。

2.3 剪切速率

剪切速率ζ常用来衡量混合器中液滴和气泡的破碎能力。剪切速率与变形速率密切相关，可以由式(9)计算得到[11,29]

(9)

式中变形速率张量D的计算公式为

(10)

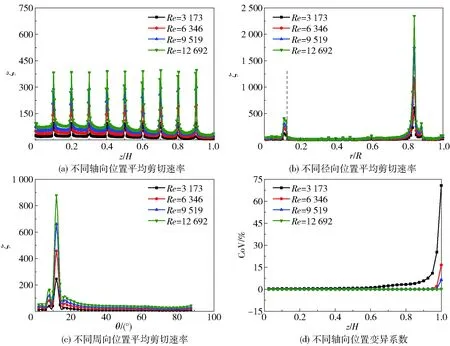
图8 αd=2.86%和t=28 s条件下不同位置处的混合性能Fig.8 The mixing performance at different locations when αd=2.86% and t=28 s

图8为轴向、径向、周向3个方向上的ζ空间分布特性。从图8(a)可以看出CJT喷嘴位置处的剪切速率与其他位置相比较大，jet1～jet9范围内平均剪切速率呈周期性波动，ζ在射流孔位置处出现峰值，说明喷嘴位置附近流体剪切能力较强。不同截面处的ζ随Re的增大而增大，在z/H=0.9处Re=6 346、9 519和12 692时的平均剪切速率与Re=3 173相比分别增大107.7%、216.6%和317.3%，表明Re的增加可有效提高对分散相液滴的破碎能力，提升混合效率。图8(b)为不同径向位置平均剪切速率受射流孔位置的影响。可以看出与其他位置相比，r/R=0.845处的ζ较大；在r/R=0.11即降液管壁面位置，与Re=3 173时相比，Re=6 346、9 519和12 692时的ζ分别增大94%、156%和240%，Re的增加使得降液管壁面处流体的扰动增强，剪切速率呈倍数增加；在r/R=0.83处，与Re=3 173时相比，Re=6 346、9 519和12 692时的ζ分别增大93%、191%和289%。从图8(c)中可以看出不同周向位置处ζ的变化趋势，在θ=12°即射流孔附近位置，射流孔初始射流速度、卷吸和掺混的共同作用使得ζ达到峰值，与Re=3 173相比，Re=6 346、9 519和12 692时的ζ分别增大86.2%、169.1%和257.7%。Re越大则射流速度越大，射流对周围流体的剪切作用也变强，从而剪切速率越大。

变异系数ICoV(CoV)可以体现流体的混合程度，其值越趋近于0表示混合程度越好，ICoV≤5%即表示流场达到混合状态[20]，其计算公式为

(11)

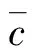
图8(d)为CoV沿轴向位置的变化趋势。由图可以看出，随着Re的增加流场混合程度提高，Re=12 692时的CoV均小于5%，表明流场内部混合基本完成。Re越小，接近于槽体顶部的流体混合程度越差，这是因为初始射流速度越小，射流对槽体顶部液体的扰动能力越差，对分散相的破碎能力也越弱。

3 结论

(1)在不同雷诺数及不同分散相相含率的条件下，射流无量纲速度具有自相似性；受两股高速射流的影响，在z/H=0.45～0.5及z/H=0.55～0.6位置处出现回流，形成强制涡。

(2)在CJT喷嘴位置处出现涡管，随〈Ω〉的增大涡管逐渐消失；受高速射流的影响在射流中心线两侧出现4对反向对涡；不同轴向位置处的〈Ω〉在射流孔位置处呈周期性波动，在z/H=0.9处，Re=6 346、9 519和12 692时的〈Ω〉与Re=3 173相比分别增大118.3%、253.7%和373.4%；与Ω、Q准则相比Liutex判别法对于CJT内细小涡结构的识别更准确。

(3)剪切速率随Re的增大而增大，在z/H=0.9处Re=6 346、9 519和12 692时的剪切速率比Re=3 173时的分别增大107.7%、216.6%和317.3%。