基于深度特征提取神经网络的滚动轴承故障诊断
2022-03-13丁春嵘周雨轩
丁春嵘 周雨轩 胡 浩 唐 刚*
(1.神华铁路装备有限责任公司, 沧州 061113; 2.北京化工大学 机电工程学院, 北京 100029)
引 言
随着我国工业化水平的不断推进,机械装备正朝着集成化、现代化和智能化的方向不断发展[1]。在众多机械设备中,旋转机械在诸如航空航天、石油化工等领域发挥着至关重要的作用,因而也对旋转机械运行的安全性和可靠性提出了更高的要求。滚动轴承作为旋转机械的重要组成部分,对其进行状态监测与故障诊断受到广泛关注[2-3]。常用的滚动轴承故障诊断方法有油液分析法、温度监测法、声发射法以及振动信号分析法等。伴随着计算机科学技术水平的显著提升以及对设备智能化要求的提高,近年来在故障诊断领域涌现出许多智能化的故障诊断方法,如专家诊断系统、模式识别诊断、灰色系统理论诊断和人工神经网络等方法[4]。其中,人工神经网络由于具有并行处理与自适应学习能力,以及较好的鲁棒性等特点,在机械设备的状态监测和故障诊断领域成为研究热点[5]。
在许多基于人工神经网络的故障诊断方法中,卷积神经网络(convolutional neural networks, CNN)是一种使用卷积运算处理网络输入且可具有深层结构的前馈型神经网络,是深度学习领域具有代表性的网络模型之一。长短时记忆网络(long short term memory network, LSTM)是循环神经网络(recurrent neural network, RNN)一种改进后的网络模型,主要用于处理长时连续信号,可有效提取其中的时序特征信息。这两类网络模型在机械设备的状态监测及故障诊断中具有较为广泛的应用。周林春等[6]将测得的滚动轴承振动信号变换为时频复数矩阵作为模型的输入,将卷积神经网络应用到复数域中,提高了滚动轴承故障诊断的准确率。闫佳瑛等[7]将滚动轴承信号经变分模态分解后,筛选出模态分量和原始信号,再将其重构成特征矩阵作为卷积神经网络的输入,使故障识别的准确率得以提升。张建付等[8]基于长短时记忆网络结合小波包变换提出一种网络模型,实现了对风电机组滚动轴承的故障诊断。杜小磊等[9]基于自编码器和长短时记忆网络模型提出一种滚动轴承故障诊断方法,可有效识别出多种故障类型及故障程度。陈伟等[10]将随机搜索算法融入到长短时记忆网络模型中,不仅提高了滚动轴承故障诊断的精度,且所提方法具有较高的鲁棒性。
滚动轴承出现故障后,随着时间的推移继续运行,故障也会不断演化。因此可以认为在测得的连续振动信号中含有丰富的时序信息,而先前常用的一些基于卷积神经网络的滚动轴承故障诊断方法无法充分提取到这些时序信息,使得诊断效果受到一定条件的制约。对于故障诊断而言,测得的滚动轴承连续振动信号中并非全部是有效信号,部分信号甚至会对诊断精度有负面效果,而常用的一些基于循环神经网络的滚动轴承故障诊断方法又无法有效识别出这些有效信息,并且当数据集较大时,时序信息过长会导致循环神经网络的计算效率降低,甚至出现模型失效。上述原因均严重制约着滚动轴承智能故障诊断方法的实际应用。
为了解决这一问题,基于卷积神经网络和长短时记忆网络这两类故障诊断网络模型的优势,本文提出一种多重特征提取的深度网络模型用于滚动轴承的故障诊断。将滚动轴承的原始振动信号作为网络模型的输入,通过多层卷积与长短时记忆层提取信号中的深层与时序故障特征信息,有效完成了多种故障模式的识别,实现了滚动轴承的智能故障诊断。
1 深度特征提取网络
1.1 卷积神经网络
卷积神经网络最先应用于计算机视觉领域,二维卷积神经网络多用于图像分类问题,通过多层卷积运算提取输入图像的特征,最终输出一组可以表征图像内容的分类概率。卷积神经网络包含3个基本组成部分:卷积层,用于提取局部特征;池化层,用于数据降维;全连接层,用于输出模型的结果。卷积神经网络可以具有较为深层的网络结构,这也就决定了其可以在特征提取时提取到数据中更为深层的特征,为后续的故障诊断提供有力帮助。卷积神经网络在故障诊断领域中的应用多存在两种形式:一是基于最初计算机视觉方向的二维应用,将一维振动信号通过分段重组的信号处理方法或是一些时频变换方法转换为二维矩阵作为网络模型的输入,提取其中的故障特征信息进而完成故障诊断;二是一维卷积神经网络,其网络的输入是一个向量和一个卷积核,输出也是一个向量,可以计算信号中的延迟积累。以滚动轴承的振动信号为例,这是一种包含时序信息的信号。在采集振动信号的过程中,当出现故障后随着时间的推移故障也会不断演化,测得的振动信号中也会包含更多的故障特征信息,利用一维卷积神经网络可以有效提取此类时序信息,得到较高的诊断精度。
卷积神经网络的特征提取过程是将卷积层和池化层交替排列逐层进行的。假设输入卷积神经网络的滚动轴承信号为X,则信号在卷积层内的特征映射可以表示为
(1)
数据经卷积层运算后,输入到池化层中。该步骤的主要作用一是将经卷积获得的高维特征降维处理,提高运算效率且可避免后续运算的过拟合;二是获得特征不变性,有效提高了模型的泛化能力。
1.2 长短时记忆网络
循环神经网络常用于处理包含时序信息的数据,其一不足是受神经元短时记忆的影响较大,即当处理一条较长的时间序列数据时,很难将数据信息从较早的时间步向后传递。为了解决“短时记忆”这一问题,人们提出了长短时记忆网络,在该网络模型内部具有被称为“门”的运算机制,可以调节网络在传递过程中的信息流。这种“门”的运算机制可以选择性地保留时序数据中的重要信息。长短时记忆网络主要包含3个部分:遗忘门层,用于选择忽略部分传递过来的长期信息;输入门层,用于传递当前状态中的长期状态给下一个同层节点;输出门层,用于输出网络模型结果。长短时记忆网络最早应用于计算机领域中的语音识别、语音合成及生成文本方面,鉴于前文提到在测得的滚动轴承振动信号中包含丰富的故障数据时序特征信息,因此使用长短时记忆网络处理滚动轴承故障信号,可以提取相对更多的故障特征信息。图1为长短时记忆网络的内部结构单元简图,其基本结构包括遗忘门、输入门及输出门。

图1 长短时记忆网络内部结构Fig.1 Internal structure of the LSTM
首先,数据经过遗忘门。数据输入到长短时记忆网络模型中后,先经过遗忘门,这一机制的作用是筛选上一时刻的单元状态,选择性地保留信息至当前单元,其数学公式描述为
ft=σ(wxf·xt+whfht-1+bf)
(2)
其次,数据经过输入门。数据经遗忘门选择性地筛选后,保留下来的信息继续向下传递至输入门,在输入门中通过激活函数运算来更新当前的单元状态,此步骤决定要保留输入数据的哪些信息,其数学公式描述为
it=σ(wxi·xt+whi·ht-1+bi)
(3)
最后,数据经过输出门。输出门用于控制数据经选择后的最终输出,输出门及单元输出的数学描述为
ot=σ(wxo·xt+who·ht-1+bo)
(4)
ht=ot·tanh(ct)
(5)
式中,遗忘门、输入门和输出门的权值参数σ均在0到1之间,wxf、whf为遗忘门变量参数,wxi、whi为输入门变量参数,wxo、who为输出门变量参数,ht-1为上一时刻从门中的输出,ct为单元状态,xt为当前单元的输入,bf、bi、bo分别为遗忘门、输入门和输出门的偏置数值。
1.3 深度特征提取神经网络模型
本文提出一种多重特征提取的网络模型用于滚动轴承的故障诊断,该网络模型的具体结构参数如图2所示。

图2 深度特征提取网络信号处理流程Fig.2 Flowchart of the deep feature extraction network
多重特征提取网络结合了卷积神经网络和长短时记忆网络模型各自的优点,除了可以提取滚动轴承的深层特征信息之外,还能够提取到输入数据中更加丰富的时序信息。在卷积层中使用分组卷积代替普通卷积,相较于常见的CNN卷积特征提取过程,可以有效避免冗余特征信息的干扰,使得模型在较少的参数下就可以提取到更多的特征信息。此外,采用分组卷积的全局加权池化,可以有效保留LSTM层提取到的时序特征信息,为后续故障样本分类提供较多的判据。
使用交叉熵函数作为智能诊断网络模型的损失函数,将损失值作为优化目标,通过多次迭代获得具有较高诊断精度的分类模型,交叉熵函数的数学公式表示为
(6)
式中,p(xi)表示真实概率分布,q(xi)表示预测概率分布。
将原始的滚动轴承信号划分样本后作为网络模型的输入,先输入至卷积层中进行深度特征提取,然后输入至长短时记忆网络运算单元用以捕捉振动信号中的动态时序信息,最后经归一化指数函数(Softmax函数)进行数据多分类进而完成滚动轴承故障诊断过程。
2 实验与结果分析
2.1 滚动轴承故障实验台
图3为凯斯西储大学的滚动轴承故障实验台示意图,实验台主要由驱动电机、扭矩传感器/编码器、测功机、加速度传感器以及控制电子设备组成。测试轴承用于支撑电机轴。实验所使用轴承型号为6205-2RS JEM SKF,轴承外径52 mm,滚动体直径7.9 mm,节圆直径39 mm。

图3 滚动轴承故障实验台Fig.3 Rolling bearing fault test bench
2.2 滚动轴承故障实验
在图3所示的实验装置上进行滚动轴承故障实验,通过电火花加工的方式生成实验轴承单点故障,在滚动轴承的内圈、滚动体及外圈的不同角度分别加工出损伤。本文实验设置加工出的故障直径分别为0.18 mm、0.36 mm、0.53 mm,故障实验的采样频率为12 kHz,转速为1 797 r/min,加载条件为0 HP,共采集到9类故障信号和1类正常运行状态下的驱动端轴承振动信号。
经滚动轴承故障实验测得的10种健康状态的信道状态信息如图4所示。由图可知在测得的振动信号中信道状态信息存在交叉现象,除少数数据点外,大部分数据的分布具有相似性,这为后续的分类诊断任务增加了难度。

图4 信道状态信息图(10种健康状态)Fig.4 Channel state information diagram (10 health states)
将凯斯西储大学轴承故障实验中测得的10种健康状态的滚动轴承振动信号划分训练样本,之后输入到网络模型中进行预训练,确定最佳的超参数值,再将全部数据以1 024个点为一个原始数据向量进行样本集划分,进而输入到网络模型中。输入数据经卷积层和长短时记忆网络门单元特征提取后,提取到的不同健康类别的特征信息再输入到Softmax函数中完成10分类任务。设置的迭代次数为50次,网络学习率为0.01,批次大小为128。样本总数为500个,其中训练集350个样本,测试集150个样本。整个过程使用的深度学习框架为谷歌公司开发的端到端开源机器学习平台。
2.3 深度特征提取网络分类结果分析
模型对振动信号分类的损失率与准确率结果分别如图5、6所示。图5表示的是将数据输入到网络模型后,模型的损失率随着迭代次数的变化情况。图6表示的是将振动信号划分训练集与测试集样本输入到模型中后,其10分类精度随迭代次数的变化过程。由图可知模型进行15次迭代即可获得较低的分类损失率与较高的分类精度,表明本文模型具有较好的收敛效果,且模型稳定后的分类准确率达到了100%。
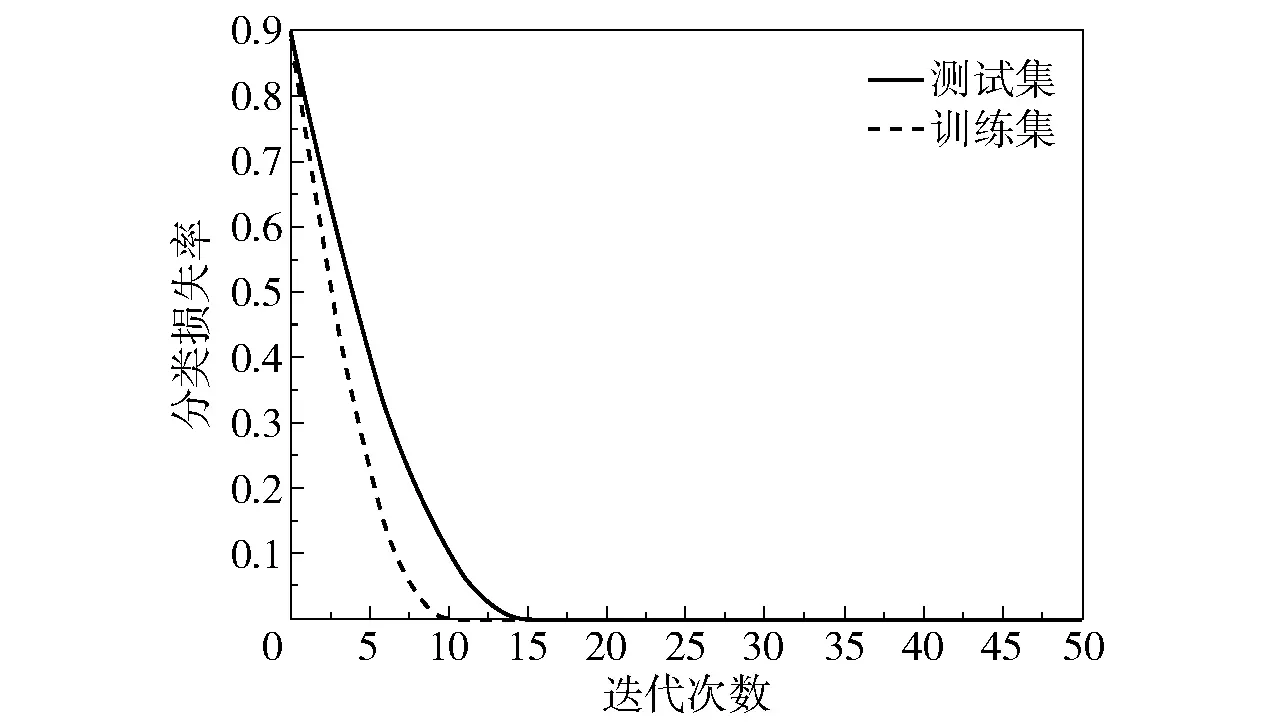
图5 模型损失率随迭代次数的变化Fig.5 Model loss ratio with different epochs

图6 模型分类精度随迭代次数的变化Fig.6 Classification accuracy with different epochs
分析图5和图6的训练结果可知,所提的深度特征提取神经网络模型具有较好的收敛效率,且分类精度较高。由图可以看到当迭代次数达到10次时,模型已基本完成了收敛,当迭代次数达到15次时模型就首次达到100%的10分类准确率,当迭代次数达到30次时,所提方法的多分类准确率稳定在100%。此外,当模型学习迭代到20~30次时,其分类准确率有轻微下降,约为0.97。出现这种现象可能是由模型首次获得了某种健康状态下的振动数据导致,但随着迭代次数的增加,这一问题会自行消失。值得一提的是本文的预训练及10分类任务均是在笔记本电脑上完成,训练一个批次的样本耗时均在10s以内,进一步说明了方法的简便性,为未来扩大应用范围与使用场景奠定了基础。
2.4 方法对比
小波分析是滚动轴承振动信号处理领域中常用的一种时频分析方法,使用小波变换来处理振动信号时其时频域的分辨率取决于分解尺度,因此可以得到振动信号中更细微的时频特征,该方法在机械振动信号故障诊断领域也有较为广泛的应用[11-12]。胶囊网络是近年来提出的一种新型网络结构,由于该网络结构具有平移同变性,在提取深度特征的同时还可以保留提取特征的相位信息,因此越来越多的研究者将其应用在滚动轴承的故障诊断领域[13-14]。有学者结合这两种方法各自的优势提出一种基于时频域改进的胶囊网络用于处理滚动轴承振动信号,进而实现故障诊断[15]。
将小波时频胶囊网络模型用于本文的故障诊断任务,并与所提模型进行对比。将测得的振动信号经小波变换时频分析处理后用作胶囊网络的输入,所得分类精度如图7所示。由图可知,该方法的稳定分类精度约为0.75,且模型精度在训练初期有较大的波动。因此在本文涉及的分类任务中,相较于本文所提方法,该方法在精度及模型的鲁棒性方面表现欠佳。

图7 小波时频胶囊网络模型分类精度Fig.7 Classification accuracy of the wavelet time frequency capsule network

图8 CNN与LSTM方法的分类精度Fig.8 Classification accuracies of CNN and LSTM
为了进一步说明所提方法的有效性,分别对CNN和LSTM进行了对比实验,两种方法在训练集和测试集上的表现如图8所示。可以看出,图8(a)中的CNN网络模型经过约45次迭代后可以获得接近100%的分类精度,然而对比图6,与本文方法相比达到同样的精度CNN故障诊断模型需要更多的迭代次数,这意味着在进行故障诊断时需要更长的时间。图8(b)中的LSTM网络模型经过约50次迭代后可以获得0.95左右的分类精度。从上述模型达到稳定精度所需的迭代次数以及最终的分类精度值来看,本文方法的效果更好。
3 结论
本文基于卷积神经网络可自动识别提取深层特征和长短时记忆网络模型可识别长连续信号中时序特征信息的优点,提出一种深度特征提取网络,实现了滚动轴承振动信号中故障信息的提取,避免了手动特征提取过程,提高了方法的时效性,并且在滚动轴承故障特征提取过程中,除了提取振动信号中的深层特征,还提取了其中的时序故障特征作为后续诊断的判据。以凯斯西储大学的滚动轴承故障数据作为方法验证,实验数据包括3种不同程度的故障数据用以模拟现实中的故障演化过程,将其中的10种健康状态数据一同作为所提网络模型的输入,在经过30次左右的迭代训练后获得了100%的分类精度,表明本文方法具有优异的故障诊断性能,且有效降低了智能故障诊断模型的复杂度。
