复习匀变速直线运动的“54321”
2022-03-12成金德
成金德
(浙江省义乌市第二中学 322000)
匀变速直线运动是运动学中最典型最基本的运动,有关匀变速直线运动的知识是运动学奠基性的内容之一,其重要性不言而喻.如何有效复习和熟练掌握相关的匀变速直线运动的知识和方法,我们认为必须紧紧抓住以下的“54321”.
1 把握五大公式
匀变速直线运动是运动学中最为典型的运动,描述匀变速直线运动规律的五大公式是运动中最为重要的关系式.
1.1 速度公式
速度公式v=v0+at是描述做匀变速直线运动的物体其速度随时间的变化规律,它涉及末速度v,初速度v0,加速度a,时间t等物理量,速度公式是一个矢量式.
例1汽车以15m/s的速度在水平路面上匀速前进,紧急制动后做匀减速直线运动,加速度大小为3m/s2,则刹车后4s时汽车的速度为( ).
A. 27m/s B. 3m/s C. 10m/s D. 0
分析由速度公式得:
v=v0+at=15m/s-3×4m/s=3m/s
可见,选项B正确.
1.2 位移公式

例2一辆汽车匀速行驶,然后以1m/s2的加速度加速行驶,从加速行驶开始,经12s行驶了180m,则汽车开始加速时的初速度为多大?

所以,汽车开始加速时的初速度为9m/s.
1.3 速度-位移关系式
例3某航母跑道长200 m,飞机在航母上滑行的最大加速度为6 m/s2,起飞需要的最低速度为50 m/s.那么,飞机在滑行前,需要借助弹射系统获得的最小初速度为( ).
A.5 m/s B.10 m/s C.15 m/s D.20 m/s

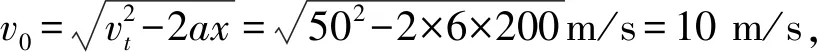
1.4 平均速度公式
例4一物体做匀加速直线运动,通过一段位移Δx所用的时间为t1,紧接着通过下一段位移Δx所用的时间为t2.则物体运动的加速度为 ( ).


1.5 推论
由匀变速直线运动的规律可推出xm-xn=(m-n)aT2.此公式是处理纸带的理论依据.
例5质点做匀加速直线运动,由A到B和由B到C所用时间均是2s,且前2s和后2s位移分别为24m和60m,求该质点运动的加速度.
分析由推论得:x2-x1=(2-1)aT2
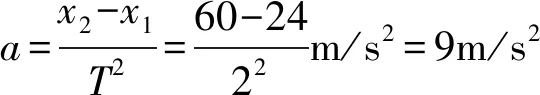
在五大公式中,共涉及v0、vt、a、t、x等五个物理量,其中每个公式中都含有四个物理量,只要知道三个物理量就可求出另外一个物理量.在运用五大公式解题时,务必注意公式的矢量性和适用性,务必注意解题的结果必须与实际问题相符合.
2 熟悉四种方法
2.1 图像法
有些问题用公式法求解会遇到麻烦,甚至无法解答,但如果使用图像法反而轻而易举.
例6某物体以一定的初速度从A点冲上固定的光滑斜面,到达斜面最高点C时速度恰为零,如图1所示,已知物体运动到斜面长度3/4处的B点时,所用的时间为t,求物体从B滑到C所用的时间.
分析先作出物体运动过程的v-t图像,如图2所示.
由数学知识可知,相似三角形面积之比等于对应边平方比,即:

图1 图2
在v-t图像中,图线与坐标轴围成的面积表示物体的位移,则S△AOC=4S△BDC
而OD=t,OC=t+tBC,将这些条件代入上式得:
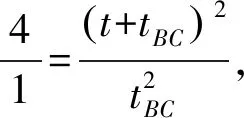
2.2 逆推法
有些问题顺着研究比较麻烦,倒过来解答就比较容易,比如解决匀减速至速度为零的运动,逆向过程就是初速度为零的匀加速运动,用逆推法解决起来更容易.
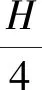

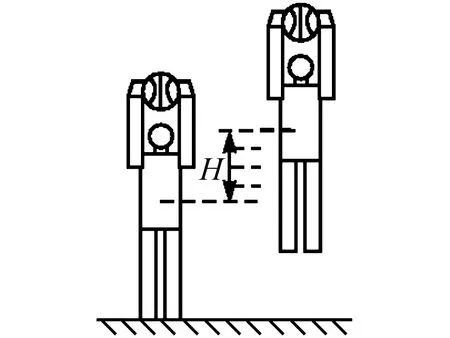
图3

2.3 相对法
取不同的参考系,有时对一些特定问题的解答会有意想不到的效果.
例8火车以速率v1向前行驶,司机突然发现在前方同一轨道上距车为s处有另一辆火车,它正沿相同的方向以较小的速率v2做匀速运动,于是司机立即使车做匀减速运动,该加速度大小为a,则要使两车不相撞,加速度a应满足的关系为( ).
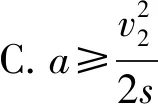

(v1-v2)2=2as
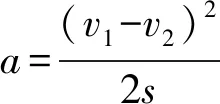
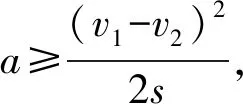
2.4 全程法
全程法是指对于某几个小过程在加速度不变的情况下,可以取全程进行研究,有时反而可以简化解题的繁琐.
例9物体在恒力F1作用下,从A点由静止开始运动,经时间t到达B点.这时突然撤去F1,改为恒力F2作用,又经过时间2t物体回到A点.求F1、F2大小之比.
分析物体在恒力F1作用下,根据牛顿第二定律得:F1=ma1
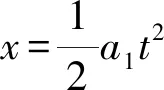
接着,物体在恒力F2作用下,先做匀减速运动,直至速度减为零,然后,物体开始返回做匀加速运动,最后回到出发点,取全程运动进行研究.
根据牛顿第二定律得:
F2=ma2
此时物体的位移为-x,由位移公式得:
由于后一过程的初速度等于前一过程的末速度,即:
v=a1t
解以上五式得:F1∶F2=4∶5
3 理解三个物理量
在运动学里,有三个重要的物理量,即位移x、速度v和加速度a.
(1)位移.描述物体位置变化的物理量,位移是矢量,用初位置指向末位置的有向线段来表示.
(2)速度.描述运动快慢的物理量,速度是矢量,用位移与发生这个位移所用时间的比值来表示.平均速度是描述某段时间(或位移)内的运动快慢,瞬时速度是描述某时刻(或某位置)的运动快慢.
(3)加速度.描述速度变化快慢的物理量,用速度的变化与对应的时间的比值来表示.加速度是矢量.
例10以下说法正确的是( ).
A.位移的大小与路程总是相等
B.速度的大小与位移的大小成正比
C.加速度的大小与速度的大小有关
D.加速度描述速度变化的快慢,但加速度的大小与速度的大小无关
分析位移和路程是两个不同的概念,只有在物体做方向不变的直线运动时,物体的位移大小才与路程相等,选项A错误;速度是描述物体位置改变快慢的物理量,速度的大小与位移的大小并无直接关系,则选项B错误;加速度的大小与速度的大小无关,选项C错误,选项D正确.
例11某物体做匀减速直线运动,其初速度为v0=20m/s,经时间t=5s,末速度vt=5m/s,方向与初速度方向相反,求:
(1)加速度多大?
(2)物体的位移多大?
(3)这段时间内物体的平均速度?
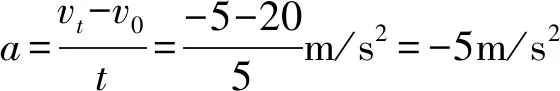
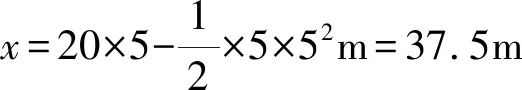
4 关注二个注意点
4.1 矢量性
由于五大公式都是矢量式,使用时必须规定正方向,与正方向一致的物理量应取正,与正方向相反的物理量应取负,在解题时务必牢记.
例12某同学将手中的“溜溜球”沿竖直方向向上抛出,已知其出手时的速度是5m/s,经过3s,该球落到抛出点下某处,速度为25m/s,已知该球在运动过程中加速度不变,则该球的加速度大小为( ).
A.6.67m/s2B.10m/s2C.8m/s2D.9m/s2
错解已知初速度v0=5m/s,末速度vt=25m/s,由速度公式v=v0+at得:
则选项A正确.
正解选取竖直向上的方向为正方向,则物体的初速度为v0=5m/s,末速度vt=-25m/s,由速度公式v=v0+at得:
加速度为负,表示加速度的方向与正方向相反,即加速度a的方向沿竖直向下方向,故选项B正确.
4.2 相符性
应用五大公式解决一些实际问题时,要注意解题的结果应与实际情况相符合.
例13汽车以15m/s的速度在水平路面上匀速前进,紧急制动后做匀减速直线运动,加速度大小为3m/s2,则刹车后6s时汽车的速度大小为( ).
A. 3m/s B. 2m/s C. 1m/s D. 0
错解由速度公式v=v0+at得:v=15m/s-3×6m/s=-3m/s,可见刹车后6s时汽车的速度大小为3m/s,选项A正确.
正解由速度公式v=v0+at可求得汽车速度减小为零的时间为:
由此可知汽车刹车5s后速度已经减小到零,第6s汽车处于静止状态,因此,刹车后6s时汽车的速度大小为零,故选项D正确.
5 处理一条纸带
利用打点计时器打出的纸带求出物体的速度和加速度是力学实验中的关键环节.
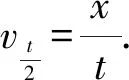
(2)求加速度.最典型的纸带是具有6段位移(共有7个计数点,这里的位移是指相邻的二个计数点间的距离)的情形,由推论xm-xn=(m-n)aT2可得:
则物体的加速度为:
例14某同学研究小车的匀变速直线运动.实验时,他将打点计时器接到频率为50HZ的交流电源上,得到一条纸带,打出的部分计数点如图4所示(每相邻两个计数点间还有4个点,图中未画出).s1=3.59 cm,s2=4.41 cm,s3=5.19 cm,s4=5.97 cm,s5=6.78 cm,s6=7.64 cm.则小车的加速度a=____m/s2(要求充分利用测量的数据),打点计时器在打B点时小车的速度vB=____m/s.(结果均保留两位有效数字)

图4
分析由于两相邻计数点间的时间间隔T=0.1 s;
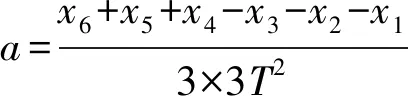
可得:
=0.80m/s2
打点计时器在打B点时小车的速度
=0.40 m/s.
总之,在复习和学习匀变速直线运动时,必须牢牢把握“54321”,注意弄清概念,理解规律,掌握方法,提高能力,以达到高效复习的目的.
