UNBOUNDED COMPLEX SYMMETRIC TOEPLITZ OPERATORS*
2022-03-12KaikaiHAN韩凯凯
Kaikai HAN (韩凯凯)
School of Mathematics and Statistics,Wuhan University,Wuhan 430072,Cnina School of Mathematics and Statistics,Hebei University of Economics and Business,Shijiazhuang 050061,China E-mail:kkhan.math@whu.edu.cn
Maofa WANG (王茂发) Qi WU (吴奇)
School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China E-mail:mfwang.math@whu.edu.cn;whuqwu@whu.edu.cn
Abstract In this paper,we study unbounded complex symmetric Toeplitz operators on the Hardy space H2(D) and the Fock space F2.The technique used to investigate the complex symmetry of unbounded Toeplitz operators is different from that used to investigate the complex symmetry of bounded Toeplitz operators.
Key words Toeplitz operator;Hardy space;Fock space;complex symmetry
1 Introduction
Guo and Zhu[2]raised the following challenge:
Characterize a complex symmetric Toeplitz operator on the Hardy space H2of the unit disk.
In recent years,bounded complex symmetric Toeplitz operators acting on classical Hilbert spaces of analytic functions have been extensively studied (see[5,6,8,10]).In this paper,we study unbounded complex symmetric Toeplitz operators.
Let H be a separable complex Hilbert space.Throughout this paper,by a linear operator on H we understand a linear mapping T:D (T)→H defined on a linear subspace D (T) of H.D (T) is called the domain of T.Let T:D (T)→H be a linear operator.We say that T is closed when the graph G (T) of T is closed,where G (T)={(x,Tx):x∈D (T)}.T is referred to as densely defined if D (T) is a dense subspace of H.For two unbounded linear operators T0and T,we say that T0is an extension of T,and write T⊂T0when D (T)⊆D (T0) and T0x=Tx for each x in D (T).If the closure of G (T) is the graph of a linear operator,clearlyis the“smallest”closed extension of T.In this case,we say that T is preclosed and refer toas the closure of T.Letting T be a closed linear operator,we say that a linear subspace D of H is a core for T if D⊆D (T) and the closure of G (T|D) is G (T).
A conjugation on a separable complex Hilbert space H is an antilinear operator C:H→H which satisfies〈Cx,Cy〉H=〈y,x〉Hfor all x,y∈H and C2=IH,where IHis the identity operator on H.Let T:D (T)→H be a closed,densely defined linear operator and let C be a conjugation on H.We say that T is C-symmetric if T⊂CT*C or,equivalently,if
〈CTx,y〉H=〈CTy,x〉H
for all x,y in D (T).T is called C-selfadjoint if T=CT*C (see[1]).
The outline of this paper is as follows:in Section 2,we collect some materials and give some lemmas that will be used in the sequel.Section 3 is devoted to investigating the complex symmetry of unbounded Toeplitz operators on the Hardy space.Section 4 deals with the complex symmetry of unbounded Toeplitz operators on the Fock space.
2 Preliminaries
2.1 Unbounded Toeplitz operators on the Hardy space
Let L2(T) be the Lebesgue (Hilbert) space on the unit circle T,and let L∞(T) be the Banach space of all essentially bounded functions on T.It is well-known thatis an orthonormal basis for L2(T).If φ∈L2(T),then the function φ is expressed as φ=,wheredenotes the n-th Fourier coefficient of φ.The Hilbert Hardy space,denoted by H2(D),consists of all functions f analytic on the open unit disk D with the power series representation

or equivalently,with

It is clear that H2(D)=span{zn:n=0,1,2,···}.For λ∈D,the reproducing kernel Kλfor H2(D) is given by Kλ(z):=and〈f,Kλ〉=f (λ) for all f∈H2(D).A function in H2(D) will be identified notationally with its boundary function.
The Cauchy integral of a function f in L1(T) is the function K f defined in D by
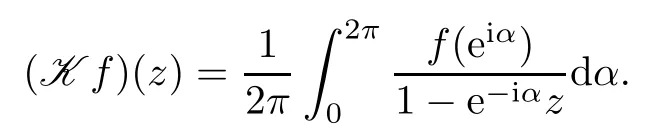
If f is in L2(T),then K f=Pf,where P is the orthogonal projection of L2(T) onto H2(D).The map fK f is continuous relative to the weak topology of L1(T) and the topology of locally uniform convergence of H (D),where H (D) denotes the space of functions analytic in D.
For φ a function in L2(T),the Toeplitz operator Tφon H2(D) is defined by Tφf=K (φf),with domain D (Tφ)={f∈H2(D):K (φf)∈H2(D)};it is a closed,densely defined linear operator,bounded if and only if φ is bounded.The domain D (Tφ) always contains H∞(D);for more details,see[11].
2.2 Unbounded Toeplitz operators on the Fock space
Let L2(μ) be the Hilbert space of all complex Lebesgue measurable functions on C which are square integrable with respect to the Gaussian measure μ defined by dμ(z)=,where dV is the Lebesgue measure on C.L2(μ) is equipped with the usual norm.Denote by F2the Fock space of all entire functions which belong to L2(μ).The canonical orthonormal basis{fn:n∈N}of F2is given by fn(z)=,z∈C,n∈N.Denote by P the set of all polynomials.
Given a Lebesgue measurable function φ on C,by a Toeplitz operator with the symbol φ we mean the linear operator Tφdefined on F2by:
D (Tφ)={f∈F2:φf∈L2(μ)},Tφf=Q (φf),f∈D (Tφ).
Here Q is the orthogonal projection of L2(μ) onto F2.
Lemma 2.1Suppose that p and q are polynomials.The following assertions are true:

Proof(i) Invoking[4,Theorem 3.2(i)],we get thatis closed.Then the conclusion directly follows from[4,Proposition 2.2,Theorem 3.2(iii)].

2.3 Some lemmas
We give some lemmas that will be used in the sequel.The following lemma is simple but basic,so we omit its proof:
Lemma 2.2Let T:D (T)→H be a closed linear operator and C a conjugation.Then CTC is a closed linear operator on H.
Lemma 2.3Let T:D (T)→H be a preclosed linear operator and C a conjugation.Then D (CTC) is a core for.
ProofIt follows from Lemma 2.2 thatis a closed linear operator.For any,it follows that Cx∈and.Then there exists a sequence (yn) in D (T) such that
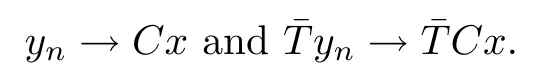
Hence,we get that Cyn∈D (CTC),Cyn→x and. □
3 Complex Symmetry of Unbounded Toeplitz Operators on the Hardy Space
Some properties of unbounded Toeplitz operators on the Hardy space were studied in[11].In this section,we investigate the complex symmetry of unbounded Toeplitz operators on the Hardy space.For φ a function in L2(T),let Ωφ:={T:T⊂Tφand T is densely defined}and we get the following result:
Lemma 3.1Let φ∈L2(T) and T∈Ωφ.Then,for every z∈D,we have Kz∈D (T*),and

Moreover,T**⊂Tφ.
ProofSince φ∈L2(T),it is clear that∈L2(T).For any z∈D,invoking[9,Corollary 1.1.29],we get that Kz∈L∞(T).A direct calculation implies that·Kz∈L2(T).
For every f∈D (T) and z∈D,it follows that

Thus,Kz∈D (T*) and T*Kz=.
Since D (T*) is dense in H2(D),it follows that T is preclosed and T**=.T∈Ωφimplies that T**⊂Tφ. □
Letting φ∈L2(T),it follows from Lemma 3.1 thatis preclosed.Then,we define Tφ,∞as the closure of.It is clear that Tφ,∞is a closed,densely defined linear operator.Moreover,(Tφ,∞)*=.
Proposition 3.2If φ∈L2(T),then⊂(Tφ,∞)*.
ProofFor every f,g∈H∞(D),we have
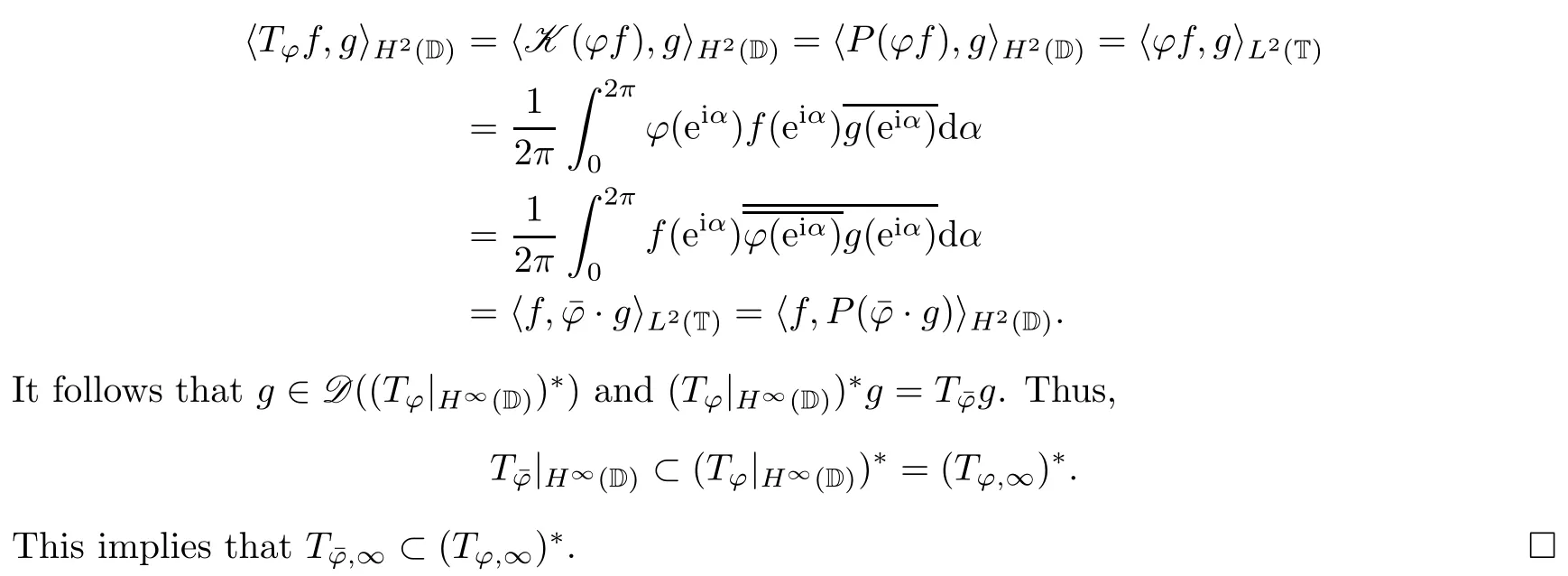
For every ξ,θ∈[0,2π],it was proved in[6]that the map Cξ,θ:H2(D)→H2(D),f (z)is a conjugation.
Proposition 3.3Let φ∈L2(T) with φ=and T∈Ωφ.If

ProofTake,arbitrarily,z,w∈D.On the one hand,

On the other hand,it follows from Lemma 3.1 that

Proposition 3.4Let φ∈L2(T) with,∀n∈Z,then the following conclusions hold:

Proof(i) It is clear that=H∞(D)=.For any g∈H∞(D),let g (w)=.For any w∈D,a calculation shows that

The following result provides a characterization of φ when the linear operator Tφ,∞is Cξ,θ-symmetric:
Theorem 3.5Let φ∈L2(T) with φ=.Then Tφ,∞is Cξ,θ-symmetric if and only if,∀n∈Z.
ProofThe proof of the necessity of this follows directly from Proposition 3.3.Conversely,let,∀n∈Z.Proposition 3.4 implies that Tφ,∞=.Invoking Proposition 3.2,we get that Tφ,∞⊂Cξ,θ(Tφ,∞)*Cξ,θ.This completes the proof. □
4 Complex Symmetry of Unbounded Toeplitz Operators on the Fock Space
Motivated by[3,4],in this section,we investigate the complex symmetry of unbounded Toeplitz operators on the Fock space F2.For every ξ,θ∈[0,2π],note that the map Cξ,θ:F2→F2,f (z)is also a conjugation.
Lemma 4.1Let φ(z)=p (z)+,where

with deg p=N,deg q=M and M,N∈N+.Then

for any z∈C.
ProofObserve that P⊆D (Tφ).Invoking[3,Corollary 1.5],we get that
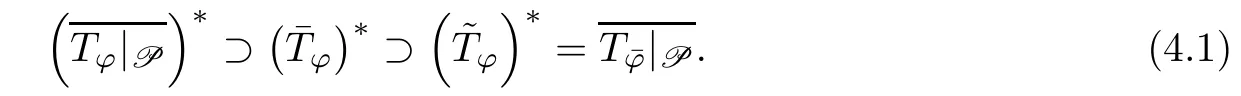
For any z∈C,by[7,Lemma 2.4]and (4.1),we get that

This completes the proof. □
Proposition 4.2Let φ(z)=p (z)+,where

with deg p=N,deg q=M and M,N∈N+.Suppose that

ProofFor any z∈C,by[7,Lemma 2.4],we get that
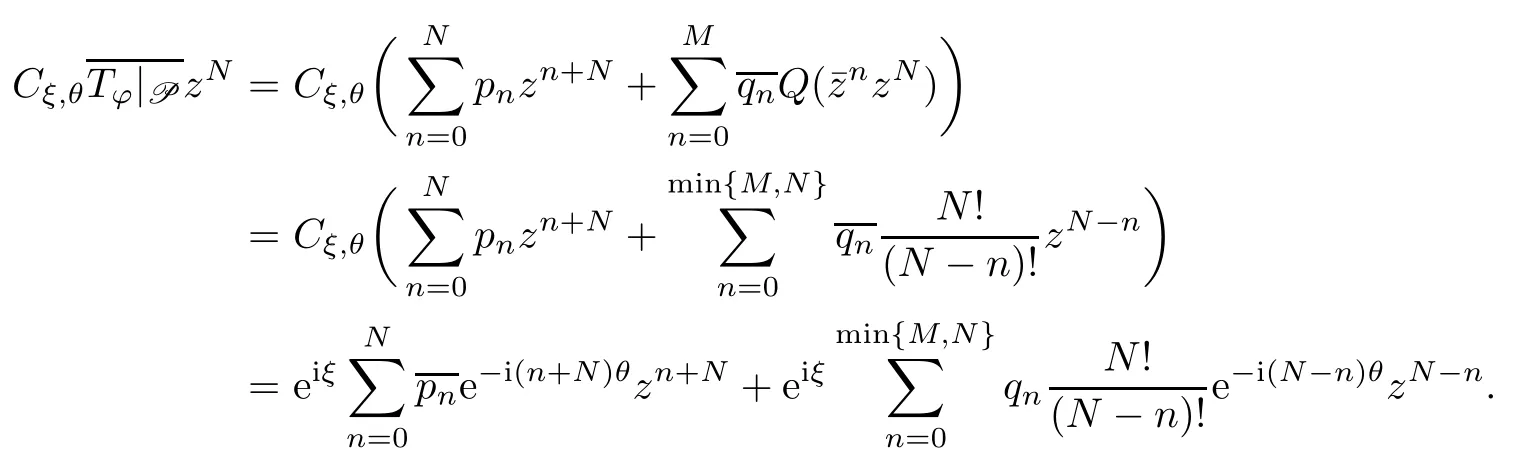
It follows from Lemma 4.1 that

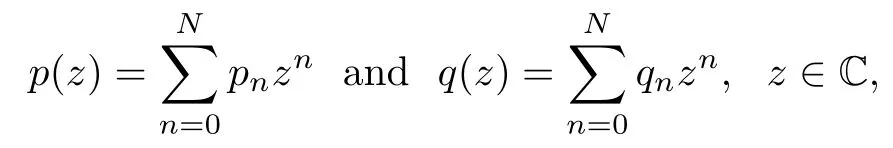
Proposition 4.3Let φ(z)=p (z)+,where=qneinθfor each 1≤n≤N,then the following conclusions hold:

Proof(i) It is easy to check that D (Cξ,θTφ|PCξ,θ)=P=.For any z∈C and k∈N,if k<N,we get that

(ii) Since Tφ|Pis preclosed,it follows from Lemma 2.3 that D (Cξ,θTφ|PCξ,θ)=P is a core for.Observing that

we get that the closure of Cξ,θTφ|PCξ,θis.Then (i) completes the proof. □
The following result characterizes the necessary and sufficient conditions for the Cξ,θsymmetry of linear operatorswith some symbol φ in the class of functions p+with polynomials p and q:
Theorem 4.4Let φ(z)=p (z)+,where

with deg p=deg q=N,N∈N+.Then Tφ|Pis Cξ,θ-symmetric if and only if=qneinθfor each 1≤n≤N.
ProofThe proof of the necessity of this follows directly from Proposition 4.2.Conversely,let=qneinθfor each 1≤n≤N.Invoking Proposition 4.3,we get that.Thus,.It follows from the proof of Lemma 4.1 that.This implies that
Our last result characterizes Cξ,θ-selfadjoint Toeplitz operators Tφwith some symbol φ in the class of functionswith special polynomials p and q.To this end,the following two propositions are needed:
Proposition 4.5Let φ(z)=,where
p (z)=pmzm+pNzN,q (z)=qmzm+qNzN,z∈C,
with 0≤m<N.Suppose that
Cξ,θTφzk=(Tφ)*Cξ,θzk,∀z∈C,∀k∈N.
ProofFor any z∈C and k∈N with k≥N-m,by Lemma 2.1 and[7,Lemma 2.4],we get that

Similarily,for any z∈C and k∈N with k<N-m,it follows from Lemma 2.1 and[7,Lemma 2.4]that

Proposition 4.6Let φ(z)=,where

Theorem 4.7Let φ(z)=,where
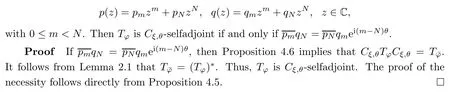
杂志排行
Acta Mathematica Scientia(English Series)的其它文章
- OPERATOR NORM AND LOWER BOUND OF FOUR-DIMENSIONAL GENERALIZED HAUSDORFF MATRICES*
- HYBRID REGULARIZED CONE-BEAM RECONSTRUCTION FOR AXIALLY SYMMETRIC OBJECT TOMOGRAPHY*
- A SPECTRAL METHOD FOR A WEAKLY SINGULAR VOLTERRA INTEGRO-DIFFERENTIAL EQUATION WITH PANTOGRAPH DELAY*
- TOEPLITZ OPERATORS FROM HARDY SPACES TO WEIGHTED BERGMAN SPACES IN THE UNIT BALL OF Cn*
- THE EXPONENTIAL PROPERTY OF SOLUTIONS BOUNDED FROM BELOW TO DEGENERATE EQUATIONS IN UNBOUNDED DOMAINS*
- ANISOTROPIC (p,q)-EQUATIONS WITH COMPETITION PHENOMENA*
