TOEPLITZ OPERATORS FROM HARDY SPACES TO WEIGHTED BERGMAN SPACES IN THE UNIT BALL OF Cn*

Ru PENG (彭茹) Yaqing FAN (范亚庆)

Department of Mathematics，Wuhan University of Technology，Wuhan 430070，China E-mail:pengru79@163.com;15071224302@163.com

Abstract We study Toeplitz operators from Hardy spaces to weighted Bergman spaces in the unit ball of Cn.Toeplitz operators are closely related to many classical mappings，such as composition operators，the Volterra type integration operators and Carleson embeddings.We characterize the boundedness and compactness of Toeplitz operators from Hardy spaces Hp to weighted Bergman spaces for the different values of p and q in the unit ball.

Key words Toeplitz operators;Hardy spaces;Bergman spaces;Carleson measure

1 Introduction

Let B={z∈Cn:|z|＜1}be the unit ball of Cn(n＞1) and S={z∈Cn:|z|=1}be its boundary.Let dυ denote the normalized Lebesgue measure of B，that is，υ(B)=1，and let dσ denote the normalized rotation invariant Lebesgue measure of S satisfying σ(S)=1.

For 0＜p＜∞，the Hardy space Hp(B) consists of those holomorphic functions f in B with

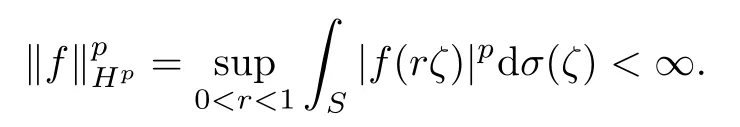
For 0＜p＜∞and α＞-1，the weighted Bergman spaceconsists of those holomorphic functions f on B with

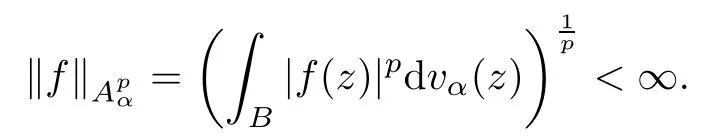
Here，dvα(z)=cα(1-|z|2)αdv (z)，where cαis a positive constant chosen so that vα(B)=1.

Let μ be a positive Borel measure on B.For λ＞0 and α＞-1 we say that μ is a (λ，α)-Bergman Carleson measure if for any two positive numbers p and q with q/p=λ there is a positive constant C＞0 such that

Given β＞-1 and a positive Borel measure μ on B，define the Toeplitz operatoras follows:

Toeplitz operators have been studied by many authors，which are closely related to many classical mappings，such as composition operators，the Volterra type integration operators and Carleson embeddings.Recently，Pau and Zhao characterized bounded and compact Toeplitz operators between weighted Bergman spaces on the unit ball in[18].Subsequently，in[21]，Pau and Perälä completely characterized the boundedness and compactness of Qμ:Hp→Hqfor the full range 1＜p，q＜∞，where

This paper is devoted to studying the boundedness and compactness of Toeplitz operators from Hardy spaces Hpto weighted Bergman spacesfor the different values of p and q in the unit ball.The proofs of this paper are inspired by the work of Pau and Zhao in[18].

Our main results are the following two theorems:

Theorem 1.1Let 0＜p，q＜∞，α＞-1.Suppose that

Let μ be a positive Borel measure on B.Then，

Theorem 1.2Let 0＜p，q＜∞，α＞-1.Suppose that

Let μ be a positive Borel measure on B.For any ε＞0，if the measure μ is a (λ，γ+ε)-Bergman Carleson measure，thenis bounded from Hpto.

Throughout this paper，C and M denote positive constants which are not necessarily the same at each appearance.The expression A≈B means that there exists a positive C such that C-1B≤A≤CB.

2 Preliminaries

In this section we introduce some notations and recall some well known results that will be used throughout the paper.

We denote the class of all holomorphic functions on B by H (B).For f∈H (B)，z∈B，the complex gradient and radial derivative are defined as

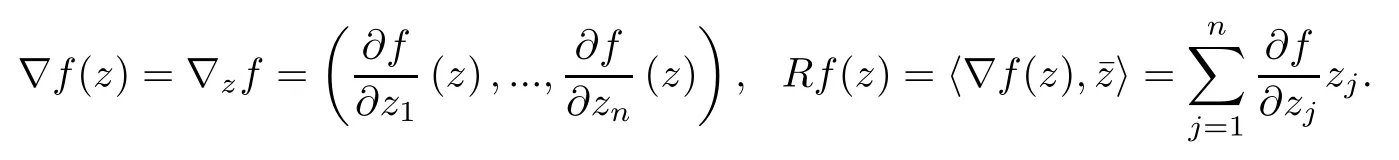
For z，w∈B，the pseudo-hyperbolic distance between z and w is defined by

ρ(z，w)=|φz(w)|，

and the hyperbolic distance on B between z and w induced by the Bergman metric is given by

For z∈B，and r＞0，the Bergman metric ball at z is given by

D (z，r)={w∈B:β(z，w)＜r}.

It is known that，for a fixed r＞0，the weighted volume is

vα(D (z，r))≈(1-|z|2)n+1+α.

We refer to[31]for the above facts.

For ξ∈S and δ＞0，let Qδ(ξ)={z∈B:|1-〈z，ξ〉|＜δ|}.For a positive Borel measure μ on B，if

then we call μ a p-Carleson measure，and if

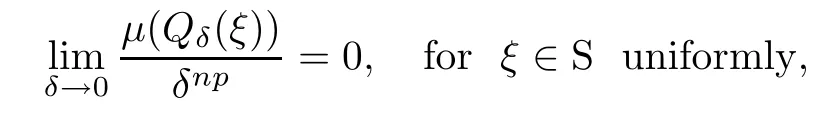
then we call μ a vanishing p-Carleson measure.

We cite two results for Bergman Carleson measures which justify the fact that a Bergman Carleson measure depends only on α and the ratio λ=q/p.The first result was obtained by several authors and can be found，for example，in[30，Theorem 50]and the references therein.

Theorem AFor a positive Borel measure μ on B，0＜p≤q＜∞，and-1＜α＜∞，the following statements are equivalent:

(i) There is a constant C1＞0 such that for any f∈，

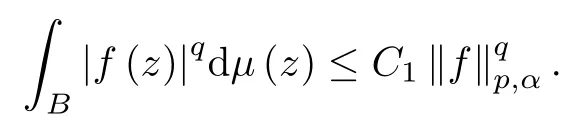
(ii) There is a constant C2＞0 such that，for any real number r with 0＜r＜1 and any z∈B，

μ(D (z，r))≤C2(1-|z|2)(n+1+α) q/p.

(iii) There is a constant C3＞0 such that，for some (every) t＞0，

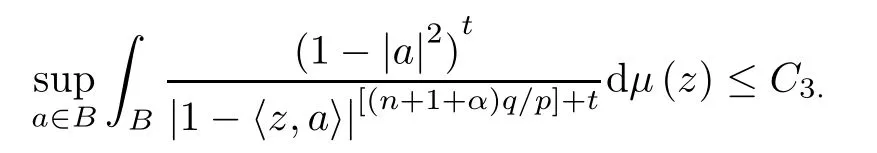
Furthermore，the constants C1，C2and C3are all comparable to‖μ‖λ，αwith λ=q/p.

Remarklet λ=q/p.Then the above result states that a positive Borel measure μ on B is a (λ，α)-Bergman Carleson measure if and only if

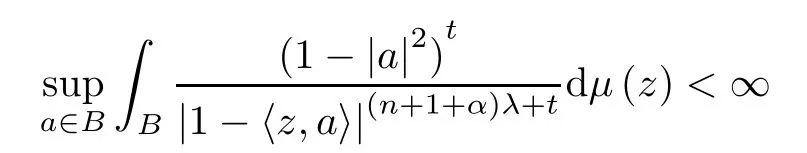
for some (every) t＞0.

For the case 0＜q＜p＜∞，we need a well-known result on the decomposition of the unit ball B.A sequence{ak}of points in B is called a separated sequence (in the Bergman metric) if there exists a positive constant δ＞0 such that β(zi，zj)＞δ for any ij.The following result is Theorem 2.23 in[31].

Lemma AThere exists a positive integer N such that for any 0＜r＜1 we can find a sequence{ak}in B with the following properties:

(i) B=∪kD (ak，r).

(ii) The sets D (ak，r/4) are mutually disjoint.

(iii) Each point z∈B belongs to at most N of the sets D (ak，4r).

Any sequence{ak}satisfying the conditions of the above lemma is called a lattice (or an r-lattice if one wants to stress the dependence on r) in the Bergman metric.Obviously any r-lattice is separated.For convenience，we will denote by Dk=D (ak，r) and=D (ak，4r).Then Lemma A says that B=and there is a positive integer N such that every point z in B belongs to at most N of sets.

The following result is essentially due to Luecking ([11]and[13])，for the case α=0(note that the discrete form (iii) is actually given in Luecking’s proof).For-1＜α＜∞，the result can be similarly proved as in[13].The condition in part (iv) first appeared in[3](see also[30，Theorem 54])，where it was used for the embedding of harmonic Bergman spaces into Lebesgue spaces.

Theorem BFor a positive Borel measure μ on B，0＜q＜p＜∞，and-1＜α＜∞，the following statements are equivalent:

(i) There is a constant C1＞0 such that for any f∈，

(ii) The function

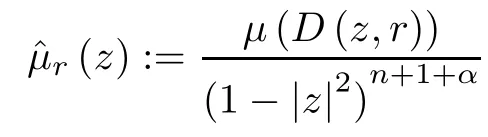
is in Lp/(p-q)，αfor any (some) fixed r∈(0，1).

(iii) For any r-lattice{ak}and Dkas in Lemma A，the sequence

belongs to lp/(p-q)for any (some) fixed r∈(0，1).

(iv) For any s＞0，the Berezin-type transform Bs，α(μ) belongs to Lp/(p-q)，α.Furthermore，with λ=q/p，one has

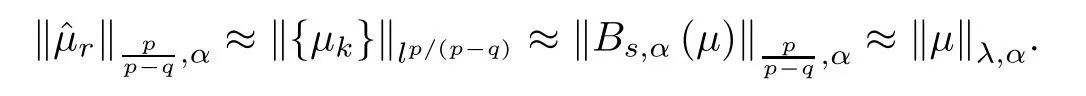
Here，for a positive measure ν，the Berezin-type transform Bs，α(ν) is

As a consequence of the previous stated result，for 0＜r＜1，a positive Borel measure μ on B is a (λ，α)-Bergman Carleson measure if and only if

for any (some) fixed r∈(0，1).

The following integral estimate (see[31，Theorem 1.12]) has become indispensable in this area of analysis，and will be used several times in this paper.

Lemma BSuppose that z∈B，c＞0 and t＞-1.The integral

is comparable to (1-|z|2)-c.

Consider a sequence of Rademacher functions rk(t)(see[5，Appendix A]).For almost every t∈(0，1)，the sequence{rk(t)}consists of signs±1.We state first the classical Khinchine’s inequality (see[5，Appendix A]for example).

Khinchine’s inequalityLet 0＜p＜∞.Then for any sequence{ck}of complex numbers，we have

With all these preparations now we are ready to prove the main results.

3 Boundedness

3.1 Proof of Theorem 1.1

Proof(i) When 0＜p≤q＜∞，we notice that λ≥1.Fix a∈B and let

fa(z)=(1-〈z，a〉)-(n+1+β).

By Theorem 1.12 of[31]，it is easy to check that fa∈Hpwith

We obtain

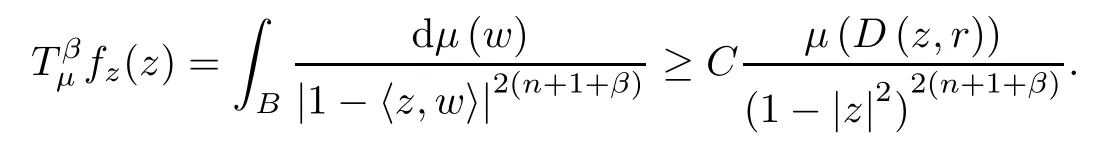
By Theorem 2.1 of[31]，together with the boundedness of the Toeplitz operator，we can get that

By Theorem A，this means that μ is a (λ，γ)-Bergman Carleson measure with

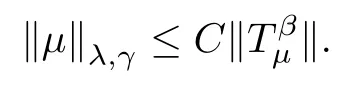
(ii) When 0＜q＜p≤2，we notice that 0＜λ＜1.Let rk(t) be a sequence of Rademacher functions and{ak}be any r-lattice on B.Since

n+1+β＞nmax{1，1/p}，

we know from Theorem 4.42 in[31]that，when 0＜p≤2，for any sequence of real numbers{λk}∈lp，the function

is in Hpwithfor almost every t in (0，1).Denote by

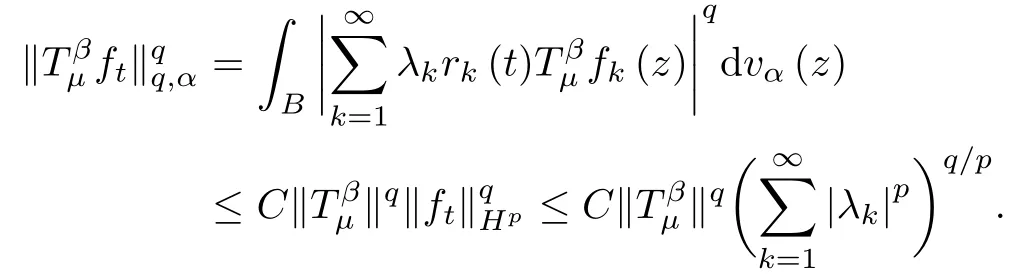
Integrating both sides with respect to t from 0 to 1，and using Fubini’s Theorem and Khinchine’s inequality，we get that

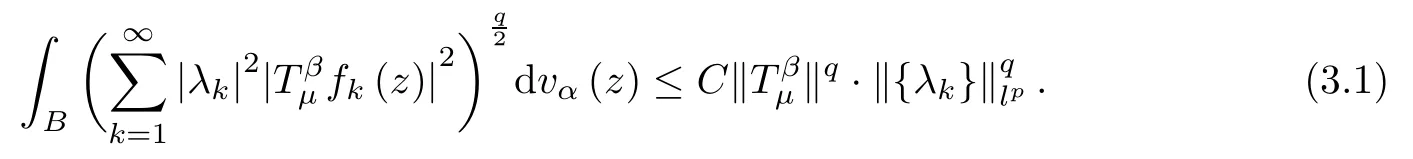
Let{Dk}be the associated sets to the lattice{ak}in Lemma A.Then

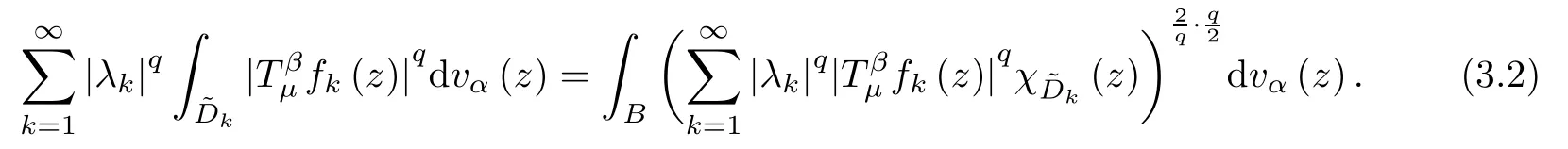
Since 0＜q＜p≤2，we can get that 2/q＞1.Thus，from (3.2) and Hölder’s inequality，we have

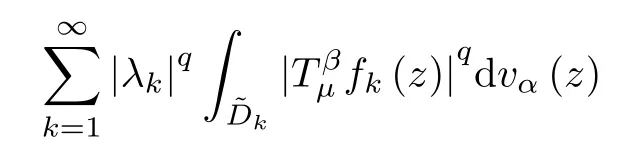
since any point z belongs to at most N of the sets.Combining the above two inequalities，and applying (3.1)，we obtain

Since，by subharmonicity (see[31，Lemma 2.24])，we have that

we get that

Now，notice that

Therefore，

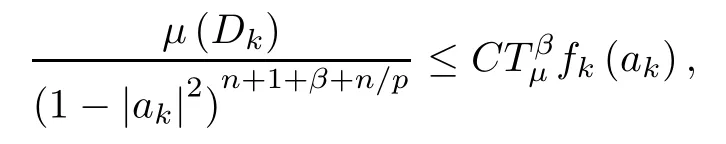
and putting this into (3.3)，we get that

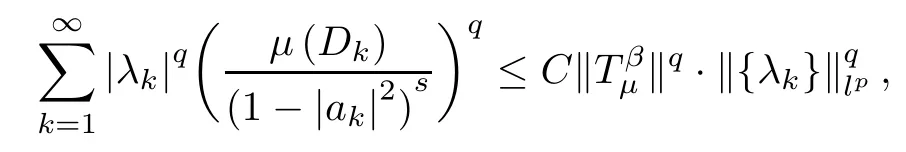
with

Since the conjugate exponent of (p/q) is (p/q)′=p/(p-q)，by duality，we know that

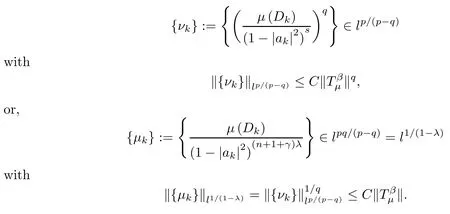
By Theorem B，this means that μ is a (λ，γ)-Bergman Carleson measure with

3.2 Proof of Theorem 1.2

ProofNow suppose that for any ε＞0，the measure μ is a (λ，γ+ε)-Bergman Carleson measure，we will prove thatis bounded.We divide the proof into three cases.

Case 1q＞1.For this case，let q′and α′be two numbers satisfying

since β＞(1+α)/q-1.By a duality result due to Luecking (see Theorem 2.12 of[31])，we know thatunder the integral pairing

Let f∈Hpand h∈，then.An easy computation using Fubini’s theorem and the reproducing formula for Bergman spaces shows that

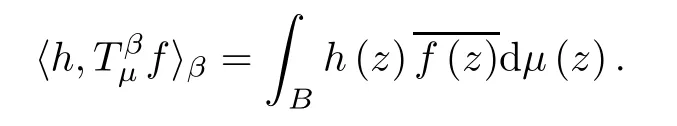
The conditions for λ and γ in the Theorem are equivalent to

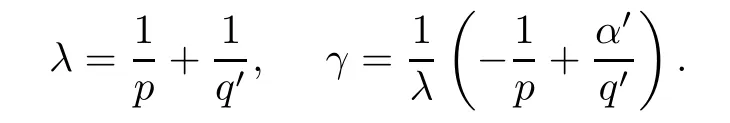
Using Hölder’s inequality，we can get that

The following inequality is well-known，and can be easily obtained by using integration by polar coordinate (see，for example，Lemma 1.8 in[31]).

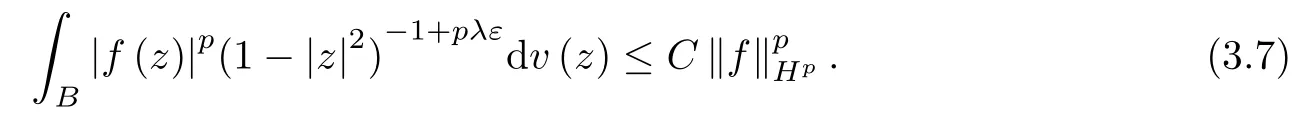
Combining (3.6) and (3.7)，we obtain that

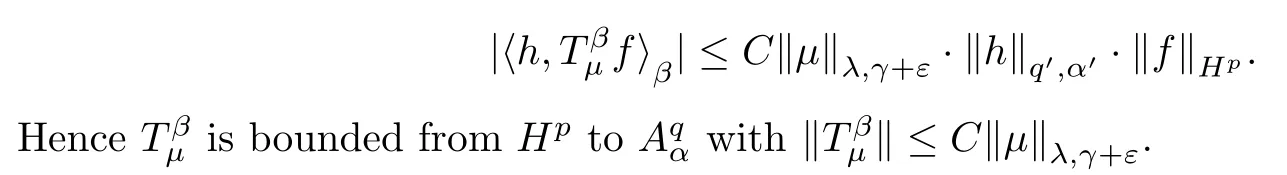
Case 2q=1.Let f∈Hp.For this case，since β＞(1+α)/1-1=α，by Fubini’s theorem and Lemma B，we have that

Let ν be the measure defined by dν(w)=(1-|w|2)α-βdμ(w).Since μ is a (λ，γ+ε)-Bergman Carleson measure，using Theorems A and B，it is easy to see that ν is a (1/p，-1+ε)-Bergman Carleson measure，and moreover，

Thus，for any f∈Hp，we have that

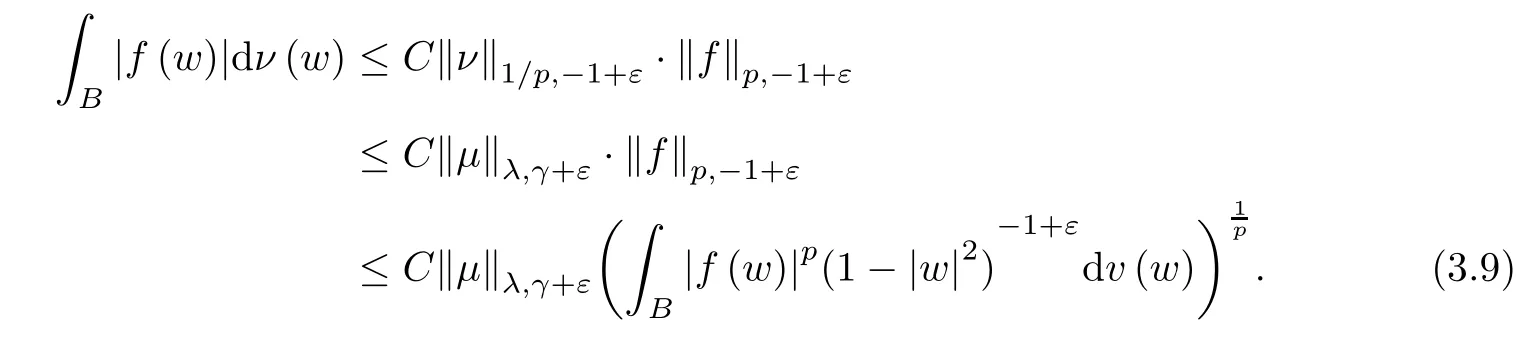
Same as in (3.7)，we have

Combining (3.8)，(3.9) and (3.10)，we obtain

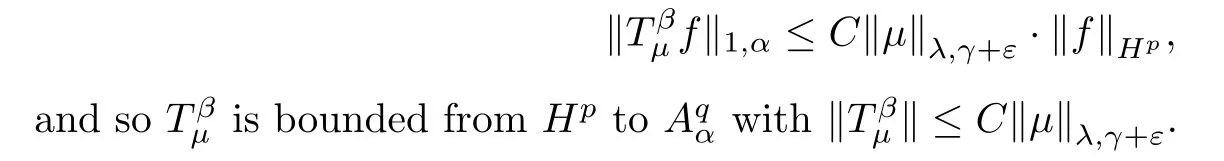
Case 30＜q＜1.Let{ak}be an r-lattice of B in the Bergman metric and let{Dk}be the corresponding sets as in Lemma A.Then we know that B=，and there is a positive integer N such that each point in B belongs to at most N of sets.Then

Now，for w∈Dk，one has that

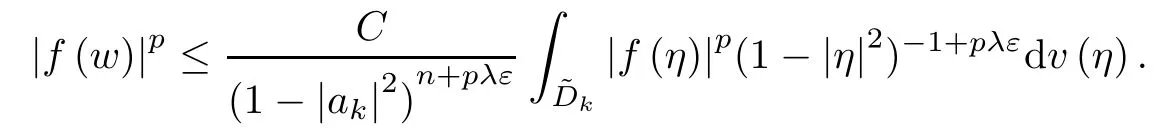
From this we get that

Since 0＜q＜1，this implies

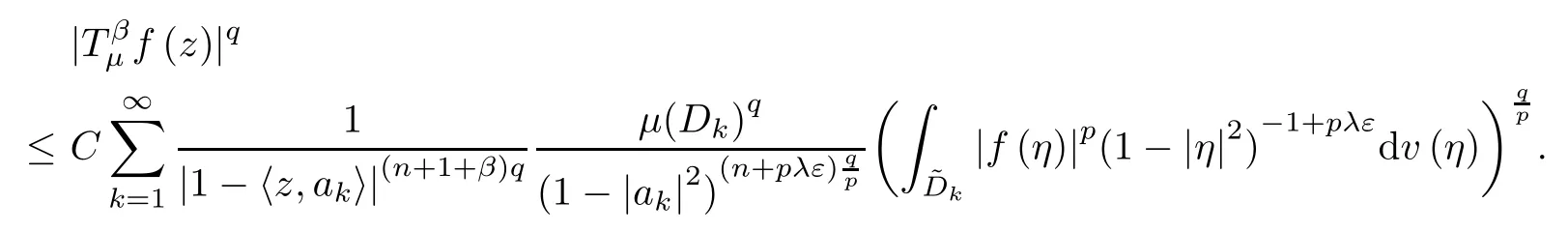
Therefore，since (n+1+β) q＞n+1+α，we can apply Lemma B to obtain

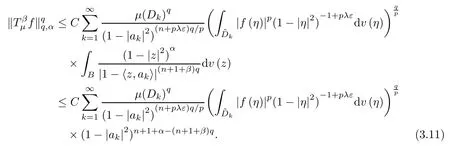
First，assume that λ≥1.Since μ is a (λ，γ+ε)-Bergman Carleson measure，by Theorem A we get that

μ(Dk)≤C‖μ‖λ，γ+ε(1-|ak|2)(n+1+γ+ε)λ.

Bearing in mind (3.4)，this together with (3.11) and the fact that q≥p (due to the assumption λ≥1)，yields

By (3.7)，we have that

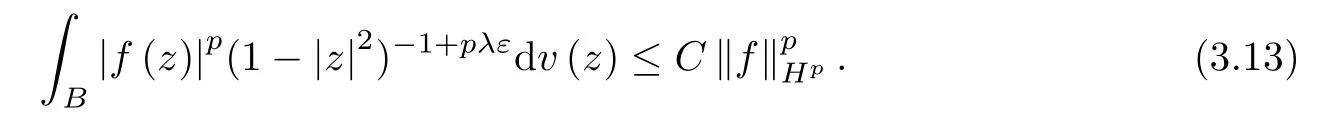
Combining (3.12) and (3.13)，we obtain

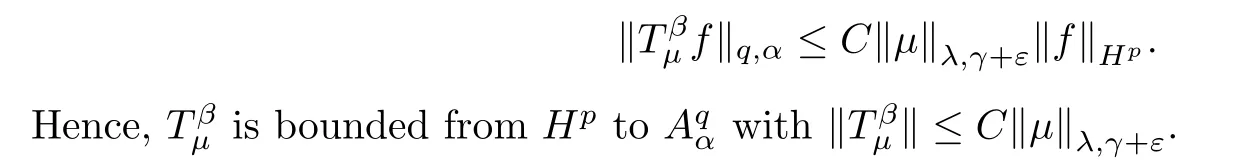
Next，assume that 0＜λ＜1.Then p＞q，and using Hölder’s inequality in (3.11)，we get that

Since μ is a (λ，γ+ε)-Bergman Carleson measure，by Theorem B，we get that

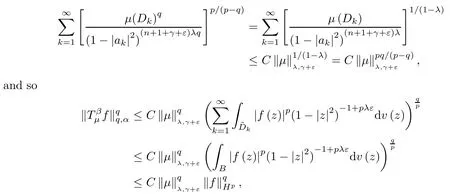
the last inequality is according to (3.13).Hence，is bounded from Hptowith

4 Compactness

We say that μ is a vanishing (λ，α)-Bergman Carleson measure if for any two positive numbers p and q satisfying q/p=λ and any sequence{fk}inwith≤1 and fk(z)→0 uniformly on any compact subset of B，

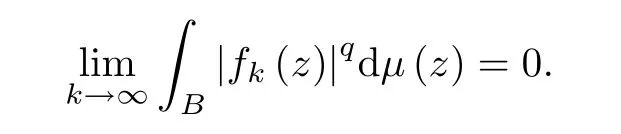
It is well-known that，for λ≥1，μ is a vanishing (λ，α)-Bergman Carleson measure if and only if

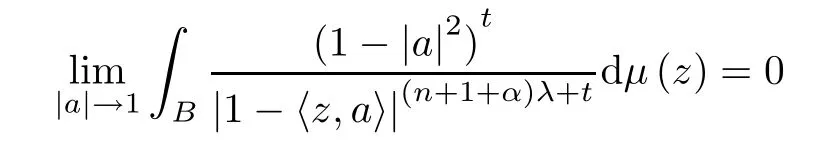
for some (any) t＞0.It is also well-known that，for 0＜λ＜1，μ is a vanishing (λ，α)-Bergman Carleson measure if and only if it is a (λ，α)-Bergman Carleson measure.We refer to[30]for the above facts.

Theorem 4.1Let 0＜p，q＜∞，α＞-1.Suppose that

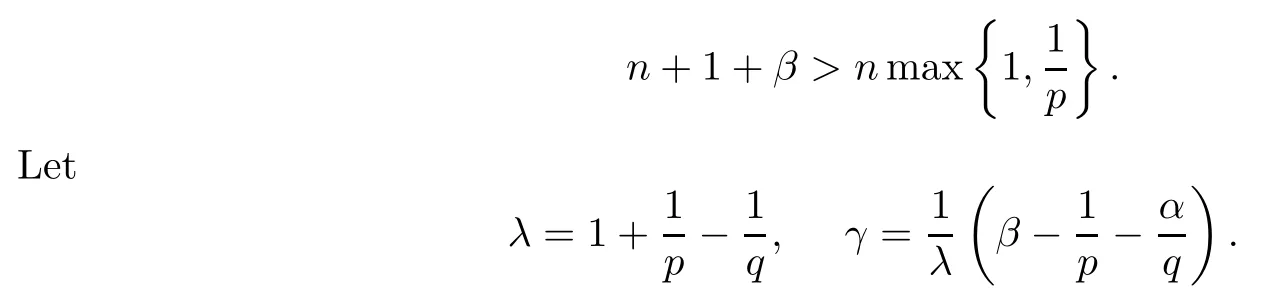
Let μ be a positive Borel measure on B.Then，

Proof(i) If 0＜p≤q＜∞，then λ≥1.Ifis compact，then→0 for any bounded sequence{fk}in Hpconverging to zero uniformly on compact subsets of B.Let{ak}⊂B with|ak|→1-and consider the functions

Thus，by[30，p.71]，the measure μ is a vanishing (λ，γ)-Bergman Carleson measure.

(ii) If 0＜q＜p≤2，then 0＜λ＜1.Sinceis compact from Hpto，it is clear thatis bounded from Hpto.By Theorem 1.1(ii)，when 0＜q＜p≤2，the measure μ is a (λ，γ)-Bergman Carleson measure.By the remark preceding Theorem 4.1，for 0＜λ＜1，μ is a vanishing (λ，γ)-Bergman Carleson measure if and only if it is a (λ，γ)-Bergman Carleson measure. □

Theorem 4.2Let 0＜p，q＜∞，α＞-1.Suppose that

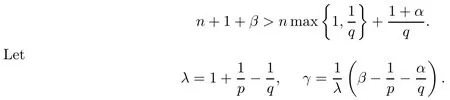
Let μ be a positive Borel measure on B.Then，

(i) when q＞1，for any ε＞0，if the measure μ is a vanishing (λ，γ+ε)-Bergman Carleson measure，is compact from Hpto;

(ii) when 0＜p≤q≤1，for any ε＞0，if the measure μ is a vanishing (λ，γ+ε)-Bergman Carleson measure，is compact from Hpto.

ProofLet μ be a vanishing (λ，γ+ε)-Bergman Carleson measure.To prove thatis compact，we must show that→0 for any bounded sequence{fk}in Hpconverging to zero uniformly on compact subsets of B.

(i) When q＞1，for this case，as the proof of Theorem 1.2，by duality we have (the numbers q′and α′are the ones defined by (3.5))

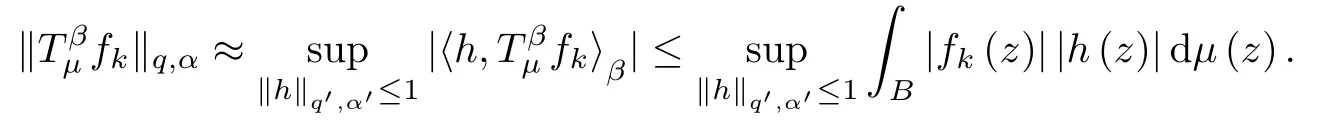
Let μr=，where Dr={z∈B，|z|＜r}.Then μris also a (λ，γ+ε)-Bergman Carleson measure，and

(see，p.130 of[4]).Similarly to the proof of (3.6)，we have that

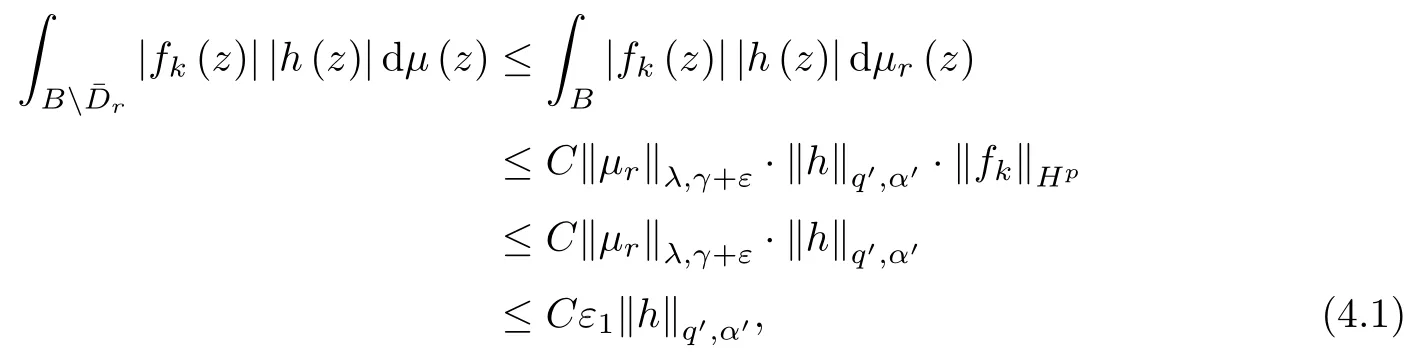
as r sufficiently close to 1.Fix such an r.Since{fk}converges to 0 uniformly in compact subsets of B，there is a constant K＞0 such that for any k＞K，|fk(z)|＜ε1for any z∈.

Therefore，by Hölder’s inequality，we can get that

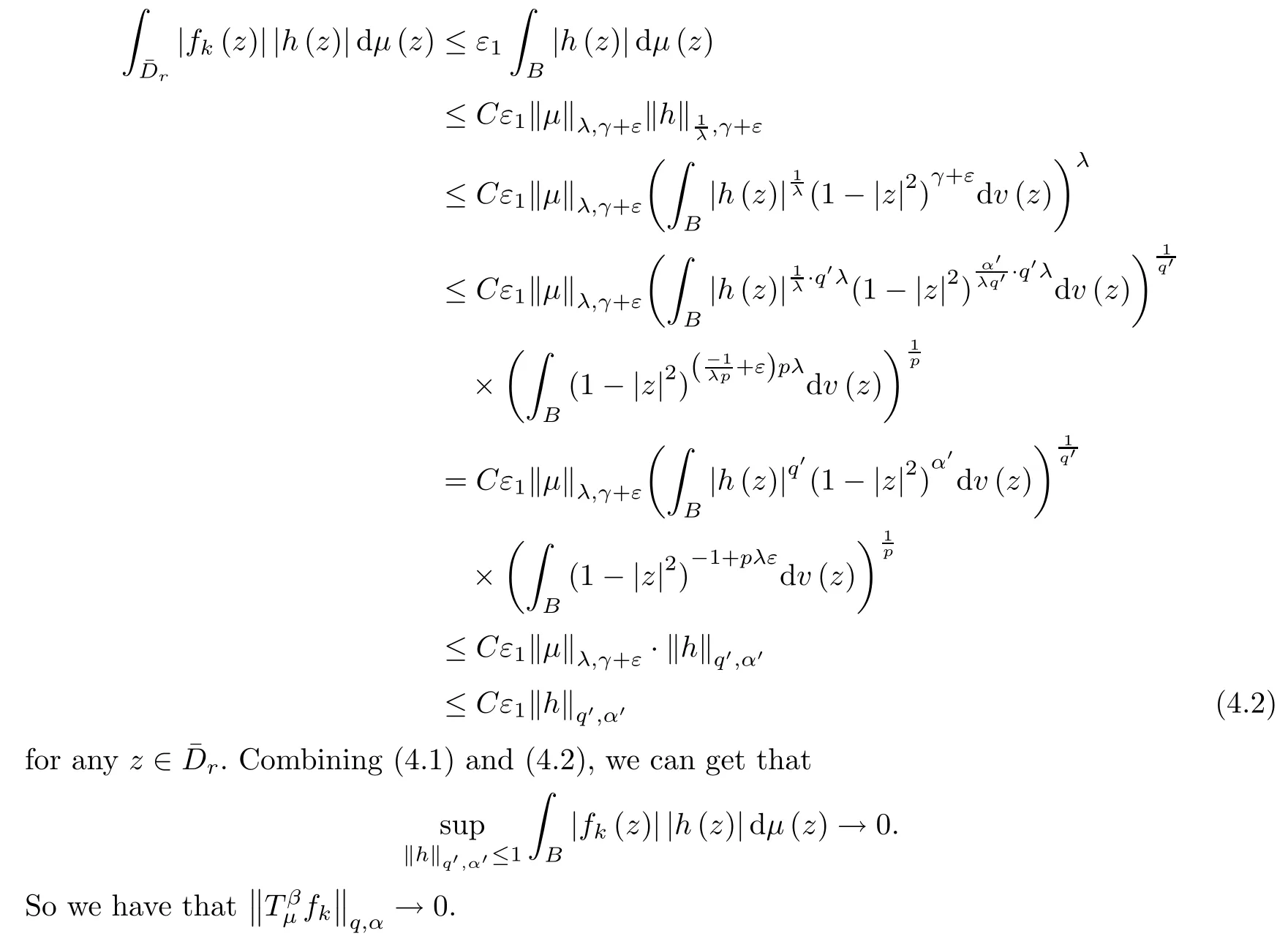
(ii) When 0＜p≤q≤1，from the estimates obtained in the proof of Theorem 1.2(see (3.11)) it follows that，for any lattice{aj}，we have that

We notice that the condition p≤q is equivalent to λ≥1.Let ε1＞0.Since μ is a vanishing (λ，γ+ε)-Bergman Carleson measure，due to[30，p.71]，there is 0＜r0＜1 such that

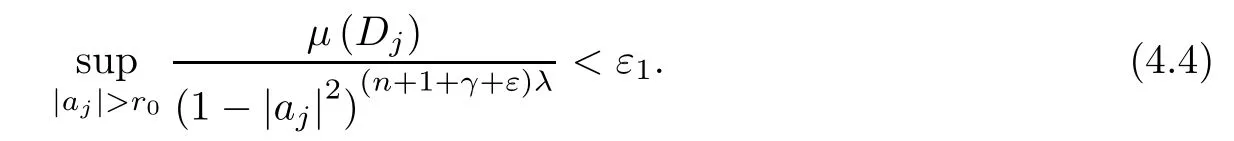
Split the sum appearing in (4.3) into two parts:one over the points ajwith|aj|≤r0，and the other over the points with|aj|＞r0.Since{fk}converges to zero uniformly on compact subsets of B，it is clear that the sum over the points ajwith|aj|≤r0(a finite sum) goes to zero as k goes to infinity.On the other hand，by (4.4)，and since q≥p，we have that

The last inequality is due to (3.13).Thus，→0，finishing the proof. □