ANISOTROPIC (p，q)-EQUATIONS WITH COMPETITION PHENOMENA*

Zhenhai LIU (刘振海)

Guangxi Colleges and Universities Key Laboratory of Complex System Optimization and Big Data Processing，Yulin Normal University，Yulin 537000，China Guangxi Key Laboratory of Hybrid Computation and IC Design Analysis，Guangxi University for Nationalities，Nanning 530006，China E-mail:zhhliu@hotmail.com

Nikolaos S.PAPAGEORGIOU

Department of Mathematics，National Technical University，Zografou Campus，15780 Athens，Greece E-mail:npapg@math.ntua.gr

Abstract We consider a nonlinear Robin problem driven by the anisotropic (p，q)-Laplacian and with a reaction exhibiting the competing effects of a parametric sublinear (concave) term and of a superlinear (convex) term.We prove a bifurcation-type theorem describing the changes in the set of positive solutions as the parameter varies.We also prove the existence of a minimal positive solution and determine the monotonicity and continuity properties of the minimal solution map.

Key words concave-convex nonlinearities;anisotropic operators;regularity theory;maximum principle;minimal positive solution

1 Introduction

Let Ω⊆RNbe a bounded domain with a C2-boundary∂Ω.In this paper we study the following anisotropic (p，q)-Robin problem:

In this problem the variable exponents p (·) and q (·) of the two differential operators are Lipschitz continuous on，that is，p，q∈.Then the two operators are defined by

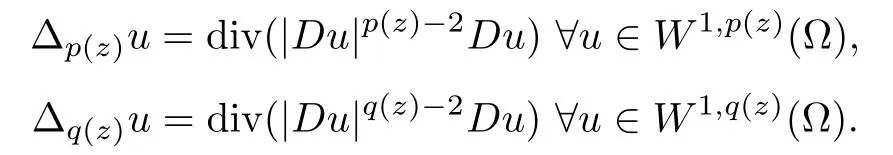
Recall that，by Rademacher’s theorem，a Lipschitz continuous function is differentiable almost everywhere (see Gasinski-Papageorgiou[13，p.56]).

In problem (pλ) the potential function ξ∈L∞(Ω) and ξ(z)≥0 for a.a.z∈Ω.In the reaction (right hand side of (pλ))，we have two terms which exhibit different asymptotic behavior as x→+∞(competing nonlinearities).One is the parametric term x→λxτ(z)-1for x≥0，with τ∈and we assume that 1＜τ(z)＜q (z)＜p (z) for all z∈.So this term is (p (z)-1)-sublinear in the sense that=0 uniformly for a.a z∈Ω(“concave”term).On the other hand，the perturbation f (z，x) is a Caratheodory function (that is，for every x∈R z→f (z，x) is measurable and for a.a z∈Ω x→f (z，x) is continuous)，which is (p (z)-1)-superlinear as x→+∞，in the sense that=+∞uniformly for a.a z∈Ω(“convex”term).To express this superlinearity of f (z，·)，we do not use the Ambrosetti-Rabinowitz condition (the“AR-condition”for short)，which is common in the literature when treating superlinear problems.Instead we assume a less restrictive condition which permits the incorporation in our framework of superlinear perturbations with“slower”growth as x→+∞，which fails to satisfy the AR-condition.In the boundary conditiondenotes the conormal derivative of u corresponding to the anisotropic (p，q)-differential operator and it is interpreted using the nonlinear Green’s identity.We mention that our conditions on the exponents p (·) and q (·) imply that

Thus，using the results of Fan[10]on boundary trace embedding theorems for variable exponent Sobolev spaces，we see that the nonlinear Green’s identity of Casas-Fernandez[4](see also Kenmochi[16]) remains valid in the present anisotropic setting.Moreover，if u∈，then

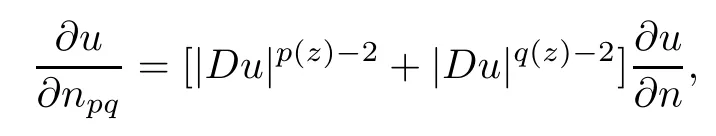
with n (·) being the outward unit normal on∂Ω.

Therefore，problem (pλ) exhibits the effects of two nonlinearities of distinct nature.One is sublinear (concave) and the other is superlinear (convex).Hence (pλ) is an anisotropic version of the classical“concave-convex problem”with Robin boundary condition.

The study of concave-convex problems was initiated with the work of Ambrosetti-Brezis-Cerami[1]，who studied semilinear Dirichlet problems driven by the Laplacian.Their work was extended to elliptic equations involving a general operator in divergence form by Molica Bisci-Radulescu-Servadei[23]and to Dirichlet equations driven by the p-Laplacian by Garcia Azorero-Manfredi-Peral Alonso[12].In the aforementioned works，the reaction has the special form

x→λxq-1+xr-1，∀x≥0，with 1＜q＜p＜r＜p*.

Extensions of these works with more general reactions and boundary conditions，can be found in the papers of Chen-Yang[5]，Leonardi-Papageorgiou[17]，Marano-Marino-Papageorgiou[19]，Motreanu-Motreanu-Papageorgiou[21]，Papageorgiou-Repovs-Vetro[28]，Papageorgiou-Zhang[31]，Papageorgiou-Vetro-Vetro[29].Of the aforementioned works，[21]studies Neumann problems driven by the p-Laplacian，while the others consider equations driven by nonhomogeneous differential operators.A common feature of all these works is that the perturbation of the concave term is nonnegative (it can not change sign).Here we remove this restriction.In the book of Motreanu-Motreanu-Papageorgiou[22]，the interested reader can find more about isotropic Dirichlet and Neumann elliptic boundary value problems.

For anisotropic problems，there is only the recent work of Papageorgiou-Radulescu-Repovs[27]on Dirichlet equations driven by the p (z)-Laplacian plus an indefinite potential.

We mention that equations driven by a combination of differential operators of different nature (such as (p，q)-equations) arise in many mathematical models of physical processes.We mention the works of Bahrouni-Radulescu-Repovs[2](transonic flow problems)，Benci-D’Avenia-Fortunato-Pisani[3](quantum physics)，Cher fils-Ilyasov[6](reaction-diffusion systems) and Zhikov[37](elasticity problems).We also refer to the two survey papers by Marano-Mosconi[20](isotropic problems) and Radulescu[32](isotropic and anisotropic problems).

Our aim in this paper is to obtain positive solutions for problem (pλ) and to determine the precise dependence on the parameter λ＞0 of the set of positive solutions of (pλ).Eventually we prove a bifurcation-type result describing the changes in the set of positive solutions as the parameter λ＞0 moves on=(0，+∞).We also show the existence of a minimal positive solutionand establish the monotonicity and continuity properties of the map λ→.

2 Mathematical Background-Hypotheses

The study of anisotropic boundary value problems uses Lebesgue and Sobolev spaces with variable exponents.A comprehensive presentation of these spaces can be found in the book of Diening-Harjulehto-Hasto-Ruzicka[8].

By M (Ω) we denote the space of all functions u:Ω→R which are Lebesgue measurable.As usual，we identify two such functions which differ only on a Lebesgue-null subset of Ω.Given any r∈，we define

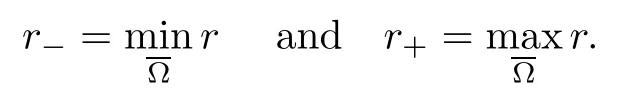
Let E1={r∈:1＜r-}.Given r∈E1，the variable exponent Lebesgue space Lr (z)(Ω) is defined by

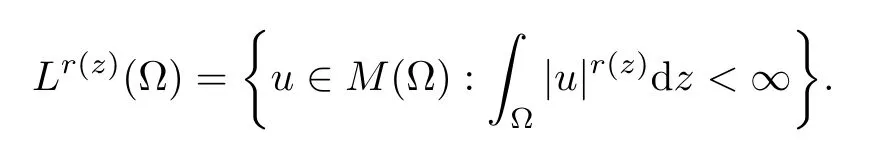
We furnish Lr (z)(Ω) with the so-called“Luxemburg norm”given by

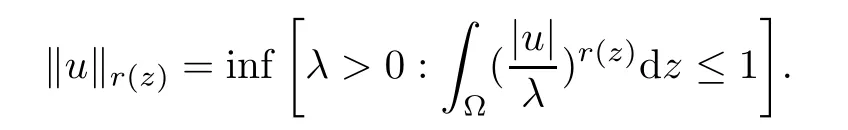
The space Lr (z)(Ω) equipped with this norm is a separable and reflexive Banach space (actually Lr (z)(Ω) is uniformly convex).Let r′∈E1be defined by=1 for all z∈.Then Lr (z)(Ω)*=，and we have the following Hölder-type inequality:

If r1，r2∈E1and r1(z)≤r2(z) for all z∈，then

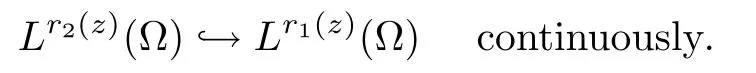
Having the variable exponent Lebesgue spaces，we can define in a natural way the variable exponent Sobolev spaces.Let r∈E1，we define

W1，r (z)(Ω)={u∈Lr (z)(Ω):|Du|∈Lr (z)(Ω)}，

with the gradient of u defined in the weak sense.

We furnish W1，r (z)(Ω) with the norm

‖u‖1，r (z)=‖u‖r (z)+‖|Du|‖r (z)，∀u∈W1，r (z)(Ω).

In the sequel，for notational simplicity，we write‖Du‖r (z)=‖|Du|‖r (z).For r∈E1，the critical Sobolev exponent corresponding to r (·) is given by

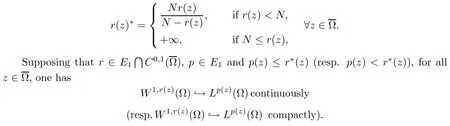
Important in the study of these variable exponent spaces is the following modular function:

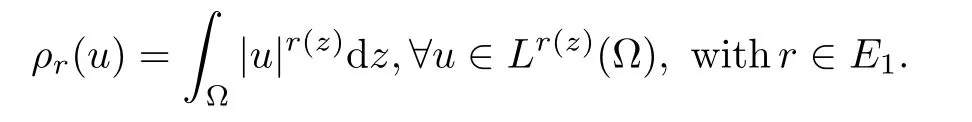
We write ρr(Du)=ρr(|Du|).The next proposition shows that there is a close relation between this modular function and the Luxemburg norm‖·‖r (z).As always，r∈E1.

Proposition 2.1(a)‖u‖r (z)=λ=1 for all u∈Lr (z)(Ω)，u0.

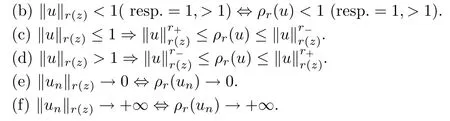
On∂Ω we consider the (N-1) dimensional Hausdorff (surface) measure σ.Using this measure，we can define as above the“boundary”variable exponent Lebesgue spaces Lr (z)(∂Ω) with r∈E1(∂Ω)=.From Fan[10]，we know that there exists a unique，linear，compact map γ0:W1，p (z)(Ω)→Lp (z)(∂Ω)(the“trace map”) such that γ0(u)=u|∂Ωfor all u∈W1，p (z)(Ω)∩.In the sequel，for the sake of notational simplicity，we drop the use of γ0(·).All restrictions of the Sobolev functions on∂Ω are understood in the sense of traces.

For r∈E1∩，we consider the nonlinear map Ar (z):W1，r (z)(Ω)→W1，r (z)(Ω)*defined by

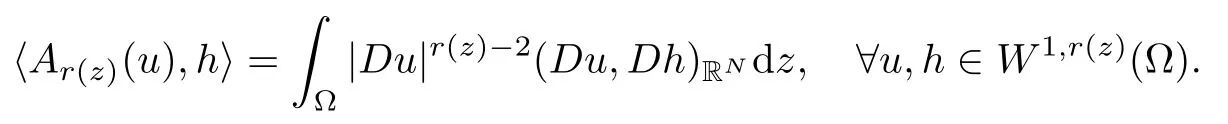
This map has the following propertics (see Gasinski-Papageongiou[14，Proposition 2.5]and Radulescu-Repovs[33，p.40]):

Proposition 2.2The map Ar (z):W1，r (z)(Ω)→W1，r (z)(Ω)*is bounded (that is，it maps bounded sets to bounded sets)，continuous，monotone (hence maximal monotone too) and of type (S)+，that is，it has the following property:

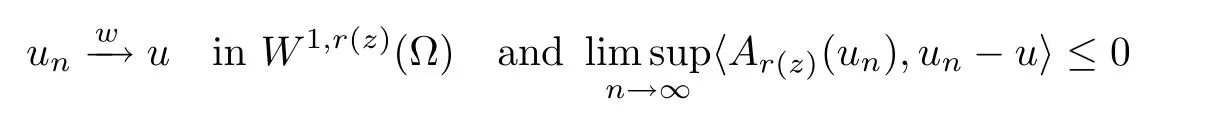
imply that

un→uin W1，r (z)(Ω).

We will also use the Banach space.This is an ordered Banach space with positive (order) cone C+=.This cone has a nonempty interior given by

We will also use another open cone in，namely the cone

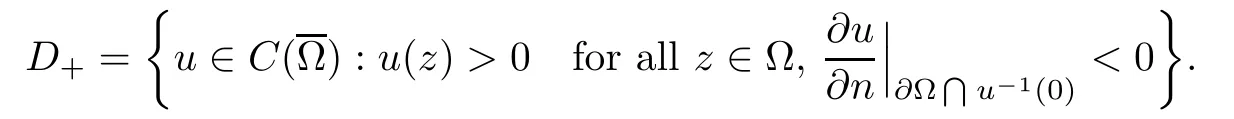
As before，n (·) is the outward unit normal on∂Ω.

If u，v∈W1，r (z)(Ω) with u≤v，we define

[u，v]={h∈W1，r (z)(Ω):u (z)≤h (z)≤v (z) for a.a z∈Ω}，

[u)={h∈W1，r (z)(Ω):u (z)≤h (z) for a.a z∈Ω}.

A set S⊆W1，r (z)(Ω) is said to be downward directed if，for every pair (u1，u2)∈S×S，we can find u∈S such that u≤u1，u≤u2.

In the sequel，for notational economy，by‖·‖we denote the norm of W1，p (z)(Ω).So

‖u‖=‖u‖p (z)+‖Du‖p (z)for all u∈W1，p (z)(Ω).

Let X be a Banach space and φ∈C1(X).We define

Kφ={u∈X:φ′(u)=0}(the critical set of φ).

We say that φ(·) satisfies the“C-condition”if it has the following property:

Every sequence{un}n≥1⊆X such that{φ(un)}n≥1⊆R is bounded and

(1+‖un‖X)φ′(un)→0 in X*as n→∞

admits a strongly convergent subsequence.

Finally，given any u∈W1，p (z)(Ω)，we define

u+=max{u，0}and u-=max{-u，0}.

We know that

u±∈W1，p (z)(Ω)，u=u+-u-，|u|=u++u-.

Next，we introduce the conditions on the data of problem (pλ).

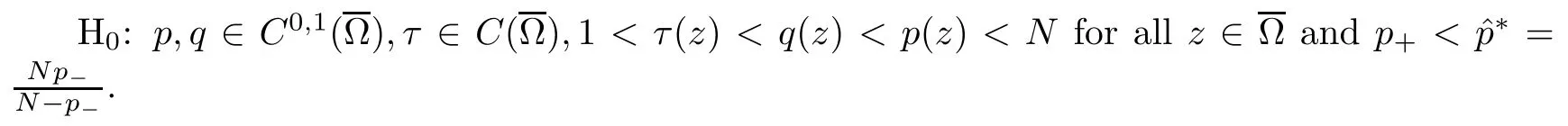
H1:ξ∈L∞(Ω)，ξ(z)≥0 for a.a.z∈Ω，β∈C0，α(∂Ω) with α∈(0，1)，β(z)≥0 for all z∈∂Ω and.

Remark 2.3This hypothesis incorporates in our framework the Neumann problem (β≡0).

H2:f:Ω×R→R is a Caratheodory function such that f (z，0)=0 for a.a.z∈Ω and

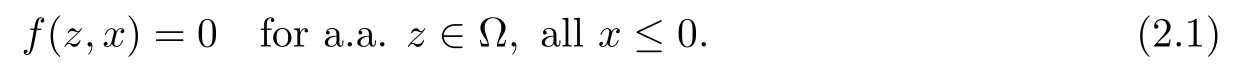
Hypotheses H2(ii)，(iii) imply that

Thus，the perturbation f (z，·) is (p+-1)-superlinear.However，this superlinearity hypothesis on f (z，·) is not formulated in terms of the AR-condition，which is common in the literature (see for example Deng[7]).Recall that the AR-condition says that there exist μ＞p+and M＞0 such that

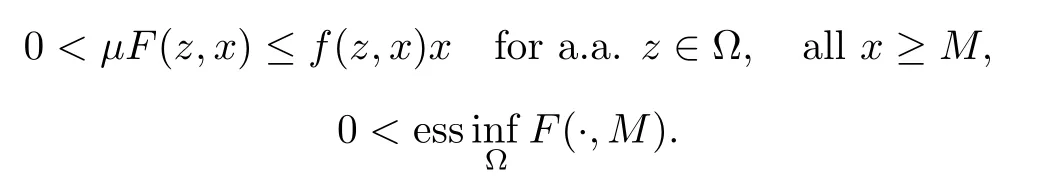
In fact，this is a unilateral version of the AR-condition due to (2.1).Integrating the first inequality and using the second，we obtain the weaker condition

This excludes from consideration nonlinearities f (z，·) with growth slower than the (μ-1)-polynomial one.For example，consider the function

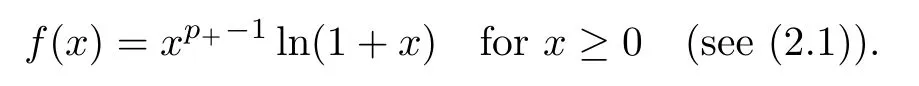
This function satisfies our hypotheses H2，but fails to satisfy the AR-condition.

Hypothesis H2(iv) says that f (z，·) is (p+-1)-sublinear near zero.Finally，hypothesis H2(v) is satisfied if，for example，f (z，·) is differentiable and for every ρ＞0，we can find＞0 such that

For ξ∈L∞(Ω) with ξ(z)≥0 for a.a.z∈Ω，ξ0，we introduce the seminorm:Lp (z)(Ω)→R defined by

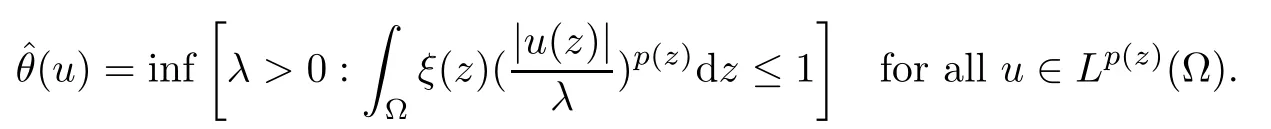
Proposition 2.5If p∈E1，ξ∈L∞(Ω)，ξ(z)≥0 for a.a.z∈Ω，ξ0，then‖·‖and|·|are equivalent norms on W1，p (z)(Ω).

ProofIt is clear from the definition of the two norms that

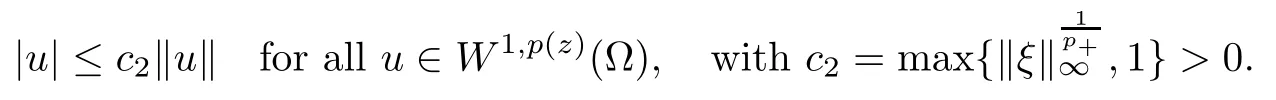
ClaimThere exists c3＞0 such that‖u‖p (z)≤c3|u|for all u∈W1，p (z)(Ω).

We argue indirectly.Suppose that the Claim is not true.Then we can find{un}n≥1⊆W1，p (z)(Ω) such that

‖un‖p (z)＞n|un|for all n∈N.

Normalizing in Lp (z)(Ω)，we see that

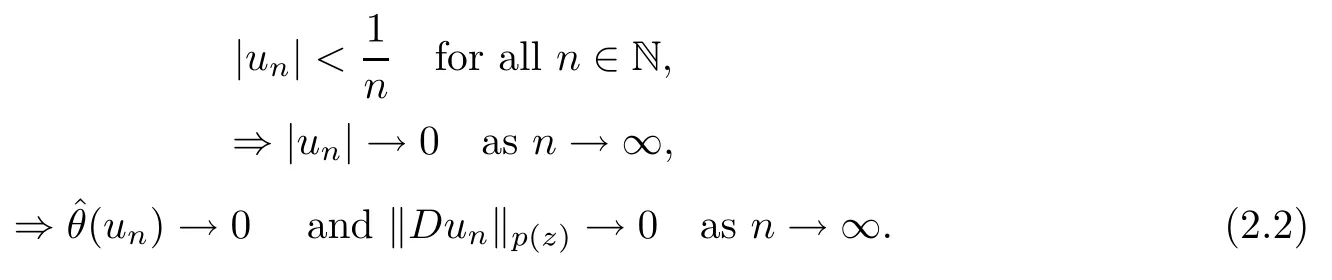
We have that

{un}n≥1⊆W1，p (z)(Ω) is bounded (recall‖un‖p (z)=1，n∈N)，

so，by passing to a subsequence if necessary，we may assume that

From (2.2) and (2.3) we have that

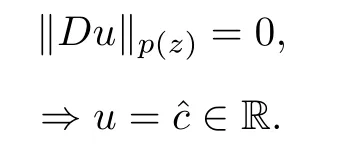
We have

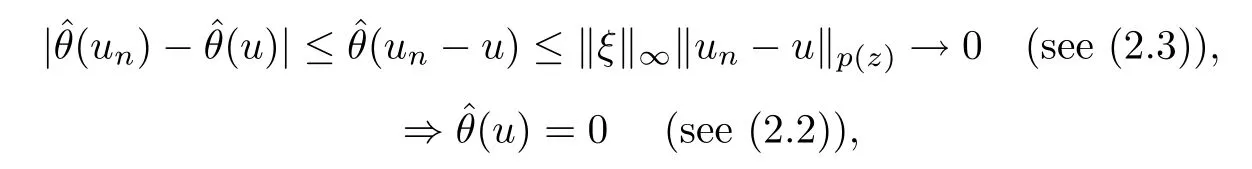
so we get

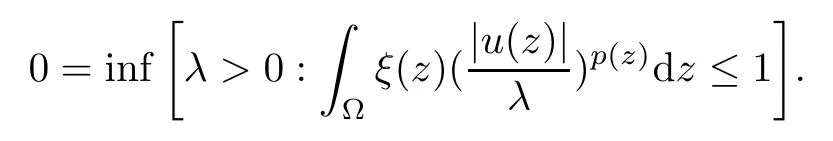
For λ∈(0，1)，we have

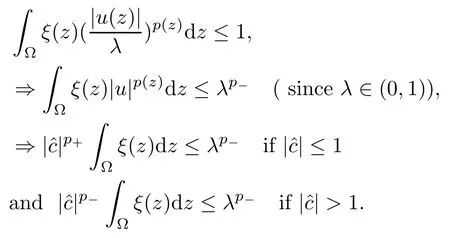
Since λ∈(0，1) is arbitrary，we let λ→0+and obtain that

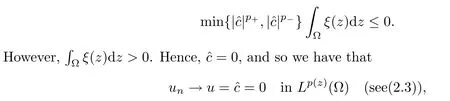
which leads to a contradiction，since by normalization in Lp (z)(Ω)，we have‖un‖p (z)=1 for all n∈N. □

Corollary 2.6If p∈E1，ξ∈L∞(Ω)，ξ(z)≥0 for a.a.z∈Ω，ξ0，then

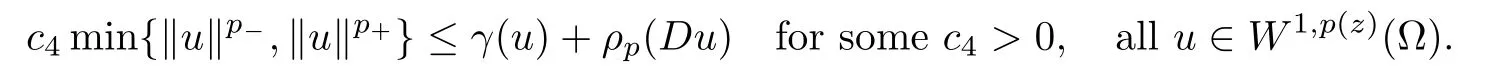
Next，let β∈L∞(∂Ω)，β(z)≥0 for σ-a.a.z∈∂Ω，β0，and introduce the seminorm η:Lp (z)(∂Ω)→R defined by

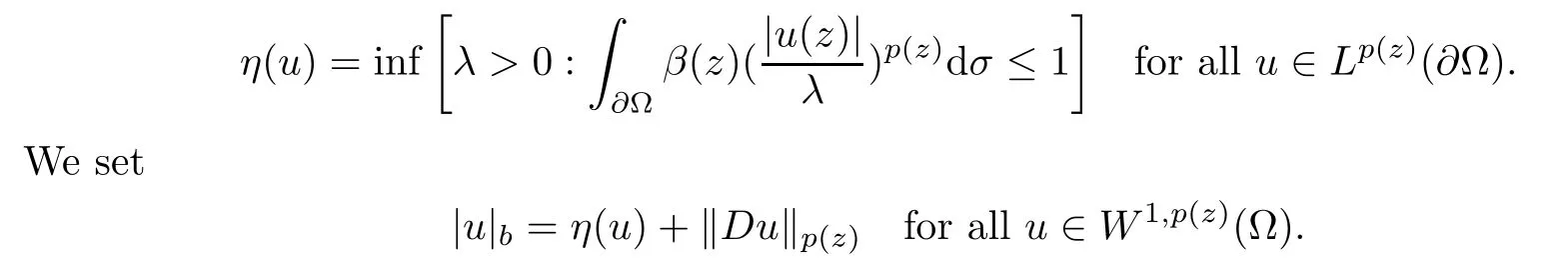
Again we easily see that this is a norm on W1，p (z)(Ω).

Proposition 2.7If p∈E1，β∈L∞(∂Ω)，β(z)≥0 for σ-a.a.z∈∂Ω and β0，then‖·‖and|·|bare equivalent norms on W1，p (z)(Ω).

ProofFrom the (compact) embedding of W1，p (z)(Ω) into Lp (z)(∂Ω)(via the trace map)，we see that

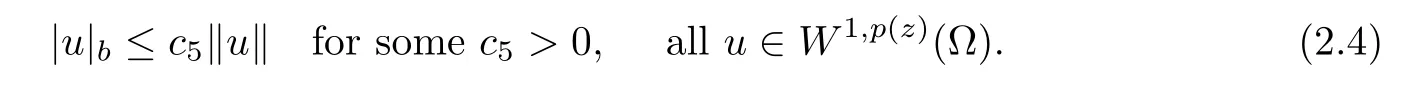
Also，via a contradiction argument as in the“Claim”in the proof of Proposition 2.5，we show that

Then，from (2.4) and (2.5)，we conclude that‖·‖and|·|bare equivalent norms on W1，p (z)(Ω). □

Corollary 2.8If p∈E1，β∈L∞(∂Ω) and β(z)≥0 for σ-a.a.z∈∂Ω and β0，then

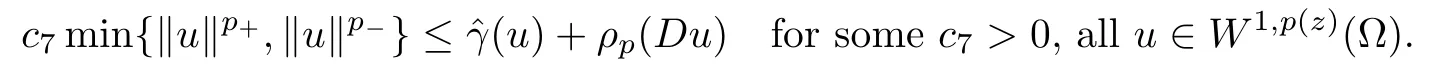
Combining Corollaries 2.6 and 2.8，we can state the following proposition:

Proposition 2.9If p∈E1and hypotheses H1hold，then

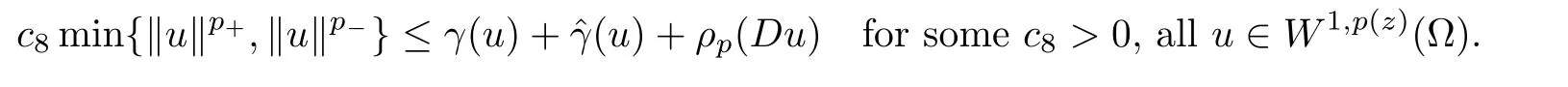
3 Existence and Multiplicity of Positive Solutions

We introduce the following two sets:

In the next proposition，we establish the nonemptiness of L and determine the regularity properties of the elements of the solution set Sλ.

Proposition 3.1If hypotheses H0，H1，H2hold，then Lφ and for all λ＞0，Sλ⊆intC+.

ProofFor η∈(0，1]we consider the following anisotropic Robin problem

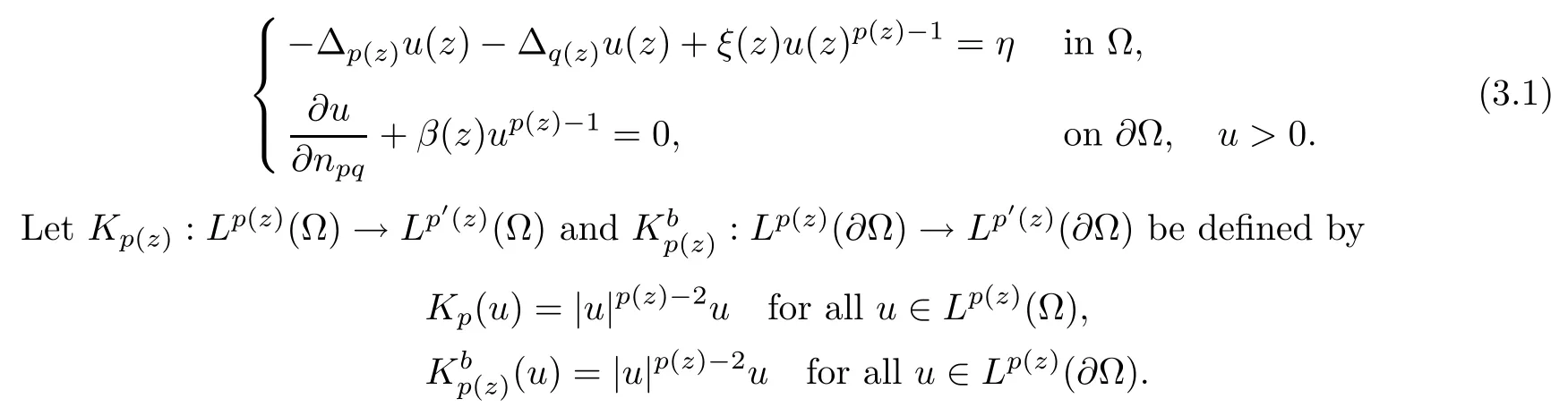
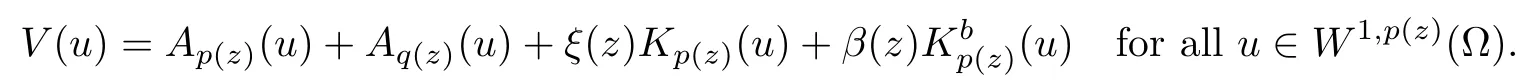
Evidently，this map is bounded (that is，it maps bounded sets to bounded sets)，continuous，monotone (see Proposition 2.2)，and thus maximal monotone.Also，for all u∈W1，p (z)(Ω)，we have that

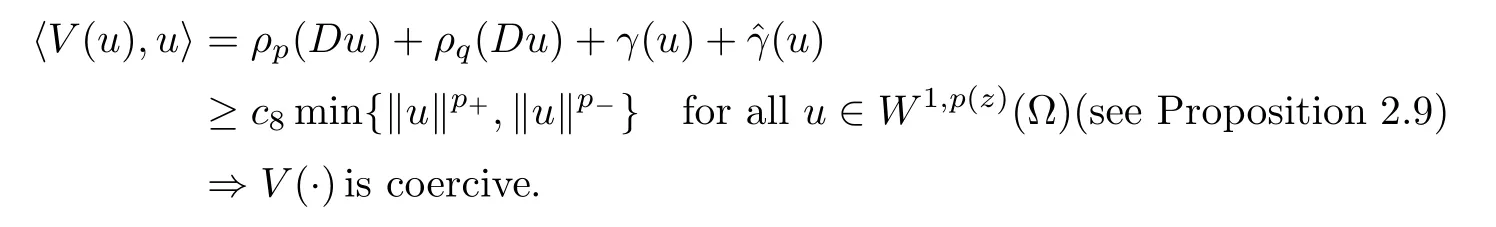
We know that a maximal monotone，coercive operator is surjective (see Papageorgiou-Radulescu-Repovs[26，p.135])，so we can findsuch that

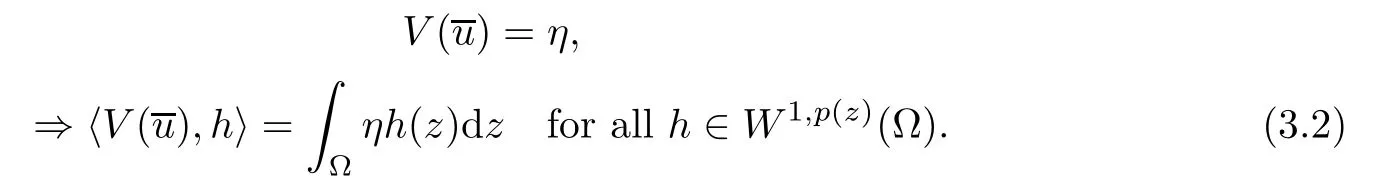
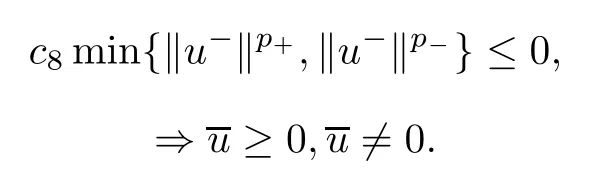
From (3.2) and the nonlinear Green’s identity (see also Papageorgiou-Radulescu-Repovs[26，p.35]，we have

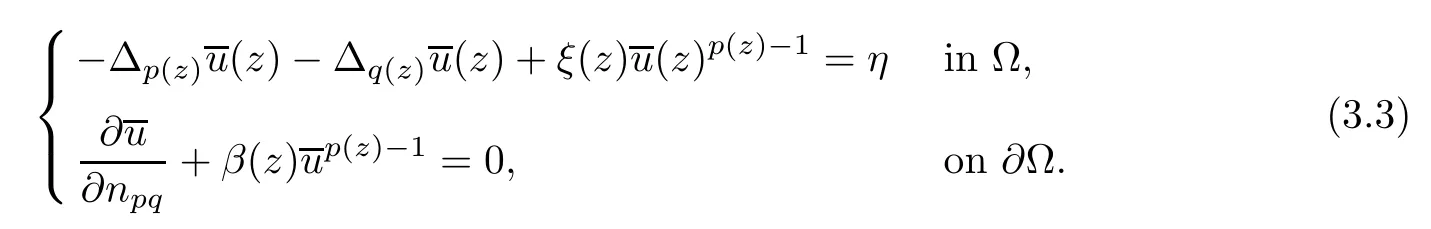
From the anisotropic regularity theory (see Fan[9]and Tan-Fang[35]and for isotropic equations Lieberman[18])，we have∈C+{0}.From (3.3) and the maximum principle of Papageorgiou-Qin-Radulescu[24](see also Zhang[36])，we have for η∈(0，1]small

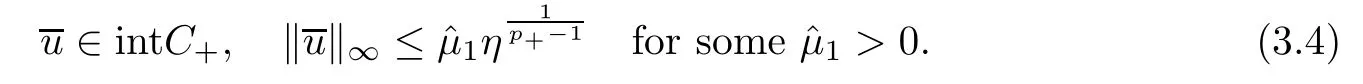
Next we show the uniqueness of this solution.To this end，we consider the integral functional j:L1(Ω)→=R∪{+∞}defined by

By Theorem 2.2 of Takač-Giacomoni[34]，the functional j (·) is convex.Let domj={u∈L1(Ω):j (u)＜+∞}(the effective domain of j (·)).

From (3.4)，(3.5) and Proposition 4.1.22(p.274) of Papageorgiou-Radulescu-Repovs[26]，we have∈L∞(Ω).Thus，if h=，then for|t|＜1 small，we have that

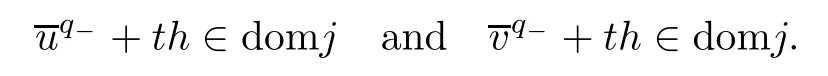
Then，on account of the convexity of j (·)，it is Gateaux differentiable atand atin the direction h，and using the nonlinear Green’s identity and the chain rule，we have that

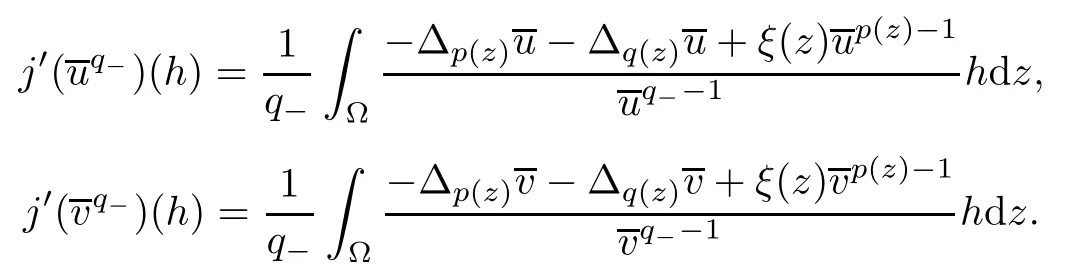
The convexity of j (·) implies the monotonicity of j′(·)，so，we have

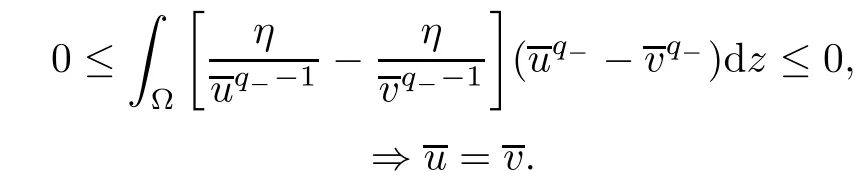
This proves the uniqueness of the solution∈intC+of (3.3).

On account of hypotheses H2(i)，(iv)，given∈∈(see (3.4))，we can find＞0 such that

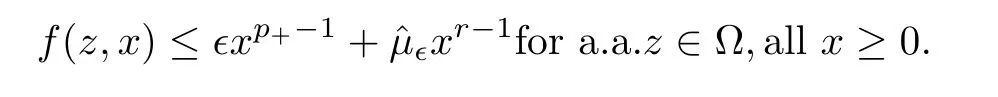
Then we have

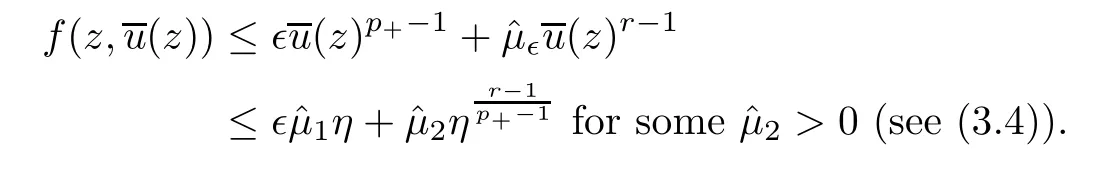
Recall that p+＜r.Then，choosing η∈(0，1]small，we can have that

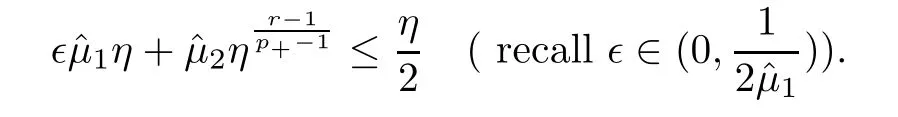
Also note that for all η∈(0，1]，for some＞0(see (3.4)).Let λ0＞0 be such that

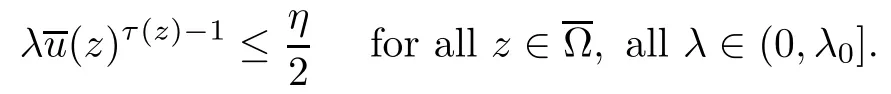
Thus，we finally have

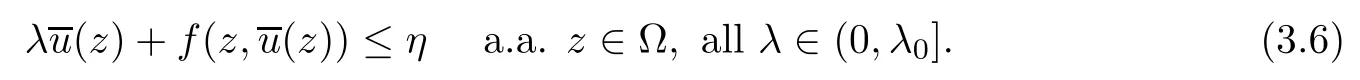
Then we have

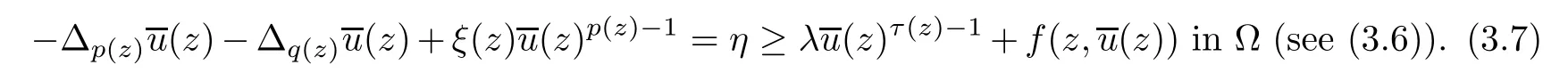
We consider the following truncation of the reaction in problem (pλ):

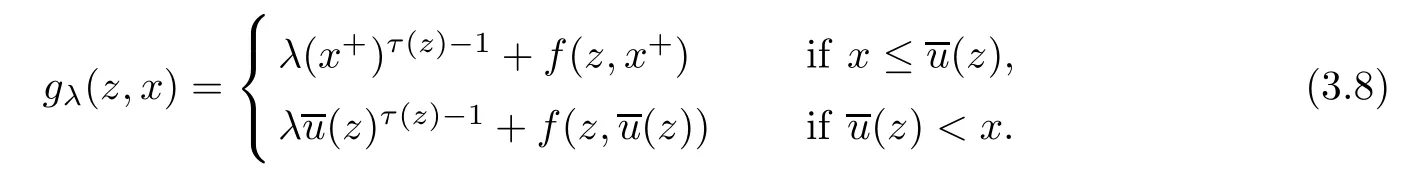
This is a Caratheodory function.We set Gλ(z，x)=and introduce the C1-functional ψλ:W1，p (z)(Ω)→R，0＜λ≤λ0defined by

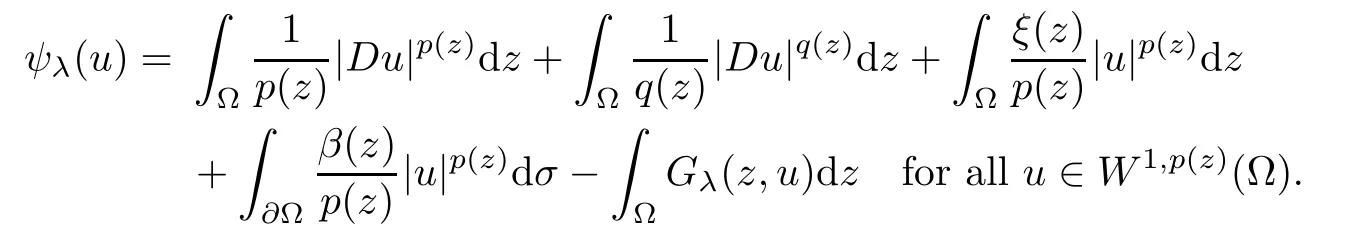
Using Proposition 2.9 and (3.8)，we see that

ψλ(·) is coercive.

Also，the compact embedding of W1，p (z)(Ω) into Lp (z)(Ω) and the compactness of the trace map imply that

ψλ(·) is sequentially weakly lower semicontinuous.

Therefore，by the Weierstrass-Tonelli theorem，we can find uλ∈W1，p (z)(Ω) such that

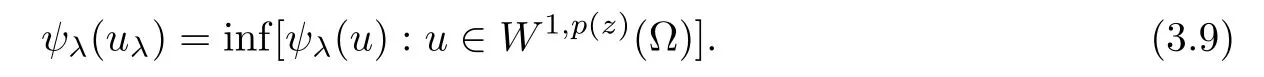
Let u∈intC+and pick t∈(0，1) small such that tu≤(see[26，p.274]，and recall that∈inf C+).Using (3.8) and hypotheses H2(i)，we have that

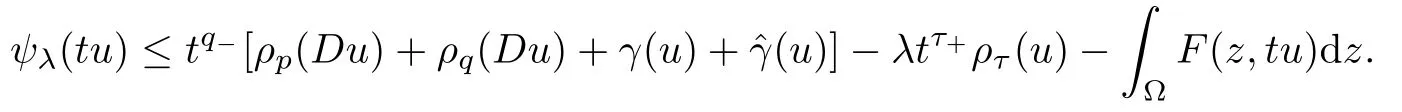
We know that τ+＜q-(see hypotheses H0)，so，using hypothesis H2(iv) and choosing t∈(0，1) even smaller if necessary，we have that

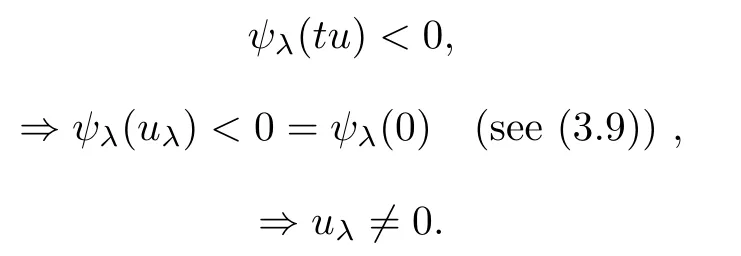
From (3.9)，we have that

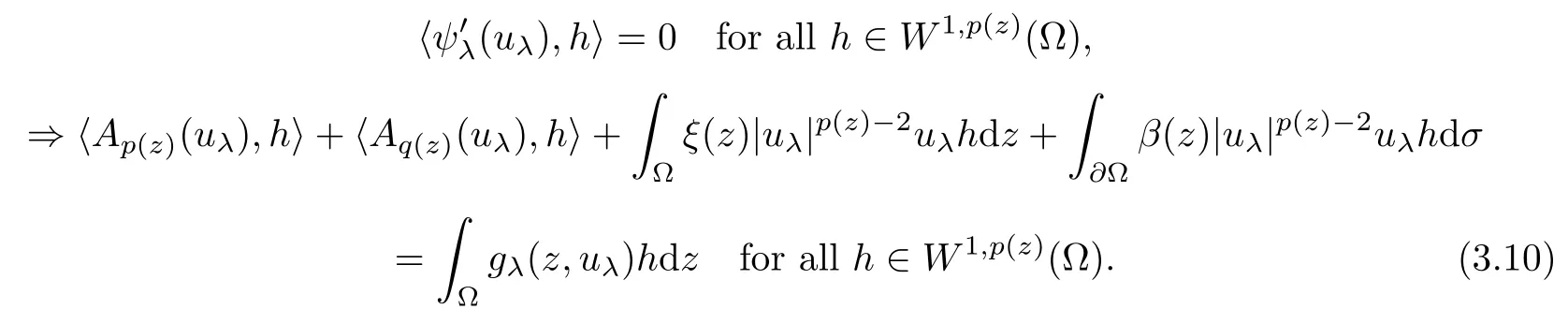
In (3.10) first we choose h=∈W1，p (z)(Ω).We obtain

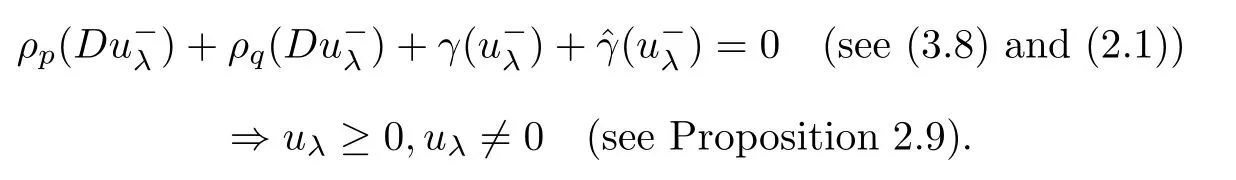
Thus，we have proved that

From (3.11)，(3.8) and (3.10)，we see that

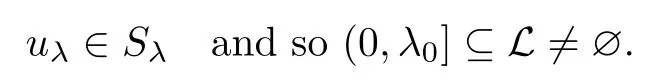
Moreover，as before，the regularity theory and the maximum principle imply Sλ⊆intC+for all λ＞0. □

Next we prove a structural property L;namely，we show that L is connected (an interval).

Proposition 3.2If hypotheses H0，H1and H2hold，and λ∈L and 0＜μ＜λ，then μ∈L.

ProofSince λ∈L，we can find uλ∈Sλ⊆intC+.Then we introduce the following truncation of the reaction in problem (pμ):

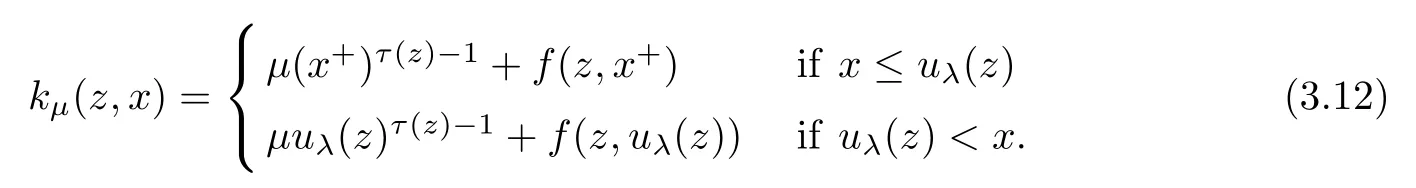
This is a Caratheodory function.We set Kμ(z，x)=and consider the C1-functional:W1，p (z)(Ω)→R defined by

As in the proof of Proposition 3.1，sinceis coercive (see (3.12) and Proposition 2.9) and sequentially weakly lower semicontinuous，we can find uμ∈W1，p (z)(Ω) such that

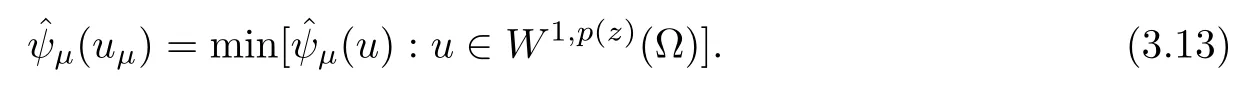
Since τ+＜q-(see hypotheses H0)，as before (see the proof of Proposition 3.1)，we show that

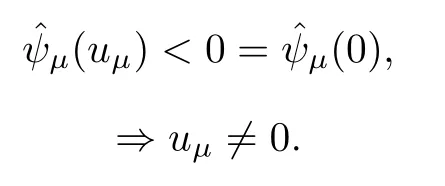
From (3.13) we have that

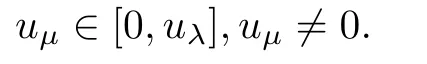
Therefore，uμ∈Sμ⊆intC+and μ∈L. □

In the above proof，in addition to showing that μ∈L，we have also proved that if uλ∈Sλ⊆intC+，we can find uμ∈Sμ⊆intC+such that uμ≤uλ.We can improve this conclusion as follows:

Proposition 3.3If hypotheses H0，H1and H2hold，and λ∈L，uλ∈Sλ⊆intC+and 0＜μ＜λ，then μ∈L，and we can find uμ∈Sμ⊆intC+such that

uλ-uμ∈D+.

ProofFrom Proposition 3.2 and its proof，we know that μ∈L，and we can find uμ∈Sμ⊆intC+such that

Let ρ=‖uλ‖∞and let＞0 be as postulated by hypothesis H2(v).We have

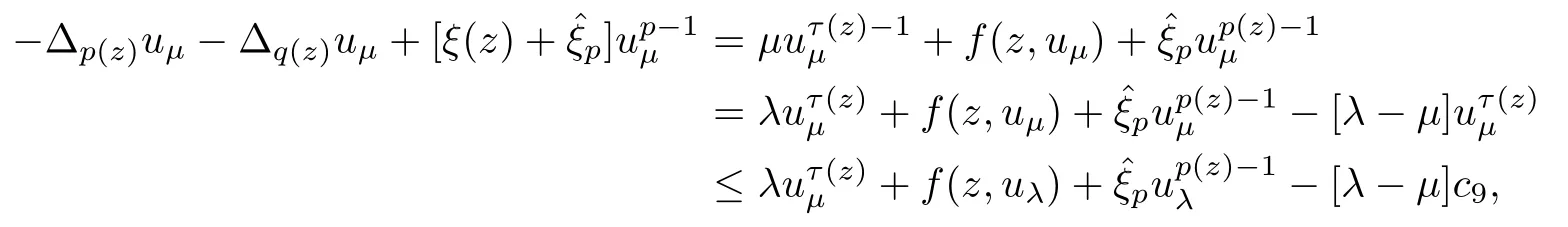
with c9=＞0，mμ=＞0 since uμ∈intC+(see (3.14)，and use hypothesis H2(v))

Since[λ-μ]c9＞0，from Papageorgiou-Qin-Radulescu[20](Proposition 5)，we infer that uλ-uμ∈D+. □

Let λ*=supL.Then we have

Proposition 3.4If hypotheses H0，H1and H2hold，then λ*＜∞.

ProofSince τ+＜q-，and using hypotheses H2(ii)，(iii) and (iv)，we see that we can find＞0 big such that

For all 0＜δ≤δ0≤1，we will have

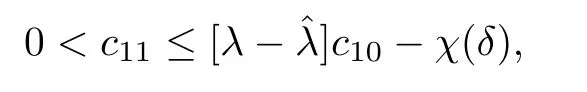
so，from (3.16) and Papageorgiou-Qin-Radulescu[20](Proposition 5)，we have

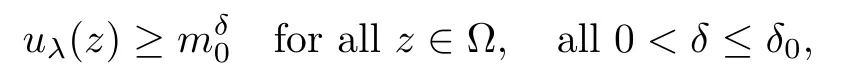
which is a contradiction.Therefore 0＜λ*≤＜∞. □

Next，we prove a multiplicity result for λ∈(0，λ*).

Proposition 3.5If hypotheses H0，H1and H2hold and λ∈(0，λ*)，then problem (pλ) admits at least two positive solutions:

ProofLet η∈(λ，λ*).We know that η，λ∈L (see Proposition 3.2).Moreover，from Proposition 3.3，we know that we can find uη∈Sηand u0∈Sλsuch that uη-u0∈intC+.We introduce the Caratheodory function eλ(z，x) defined by

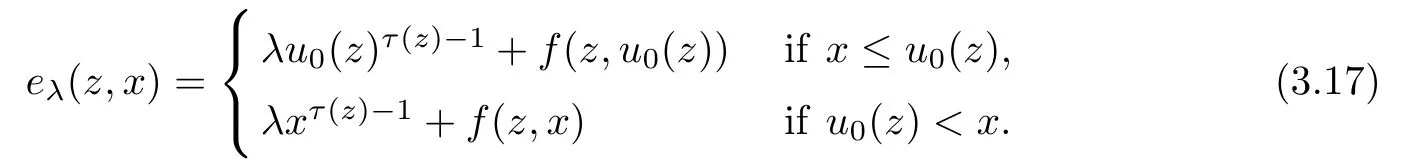
We set Eλ(z，x)=and consider the C1-functional μλ:W1，p (z)(Ω)→R defined by

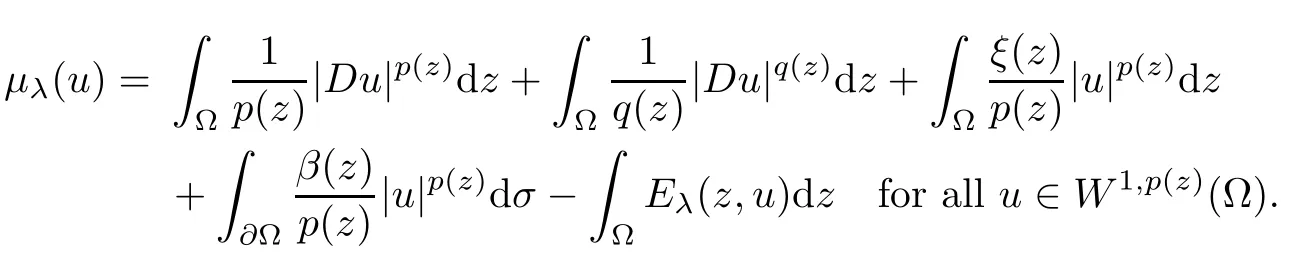
Also，we introduce the following truncation of eλ(z，·):

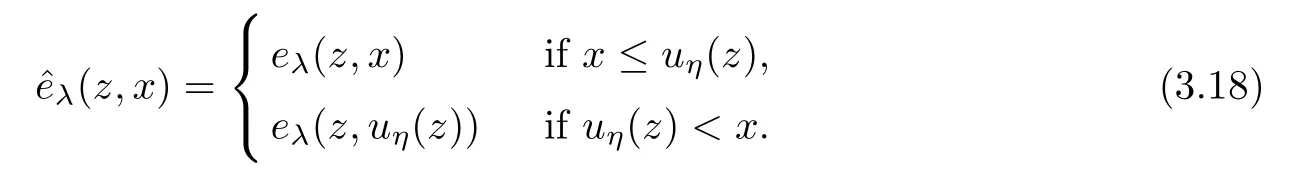
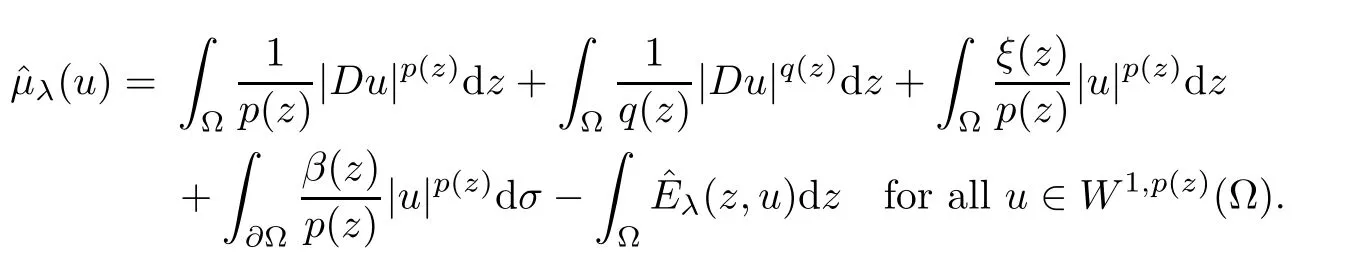
From (3.17) and (3.18) we see that

Moreover，using (3.17) and (3.18)，we easily check that

Then，on account of (3.20) and (3.21)，we infer that，without any loss of generality，we may assume that

Otherwise，we already have a second positive smooth solution bigger than u0，and so we are done.

From Proposition 3.2 and (3.18) it is clear thatis coercive，and also that it is sequentially weakly lower semicontinuous.Thus，we can find∈W1，p (z)(Ω) such that

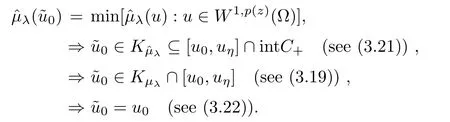
Recalling that uη-u0∈D+，it follows that

(see Gasinski-Papageorgiou[14，Proposition 3.3]and Tan-Fang[35，Theorem 3.2]).

On account of (3.20) and (3.17)，we may assume that

Otherwise，we already have an infinity of positive smooth solutions all bigger than u0and so we are done.From (3.23)，(3.24) and Theorem 5.7.6 of Papageorgiou-Radulescu-Repovs[26，p.449]，we know that we can find ρ∈(0，1) small such that

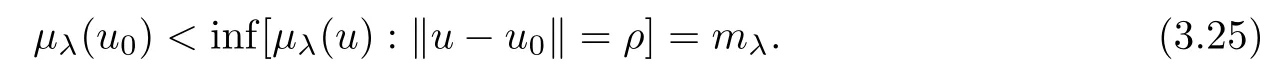
From hypothesis H2(ii) and (3.17)，we see that，if u∈intC+，then

Claimμλ(·) satisfies the C-condition.

Let{un}n≥1⊆W1，p (z)(Ω) such that

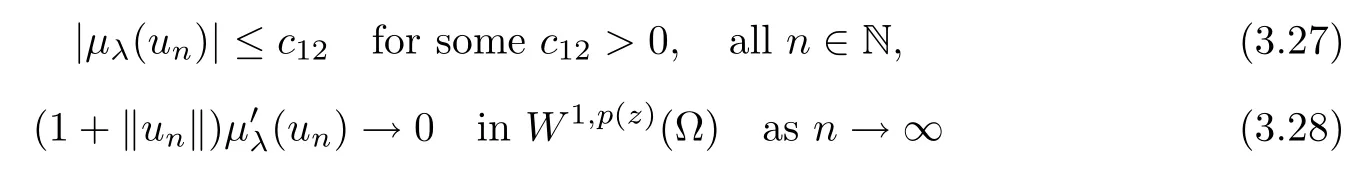
From (3.28) we have that

Then，from (3.27) and (3.30)，it follows that

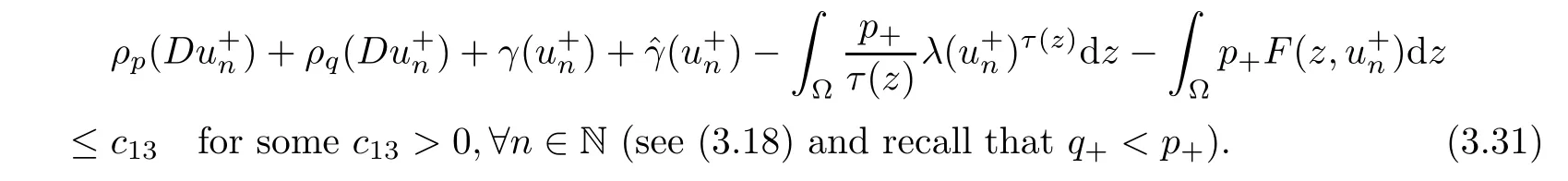
On the other hand，from (3.29)，with h=∈W1，p (z)(Ω)，we have that

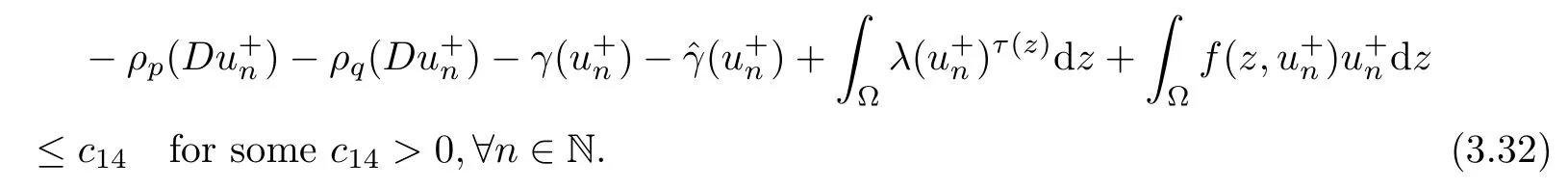
We add (3.31) and (3.32) and obtain

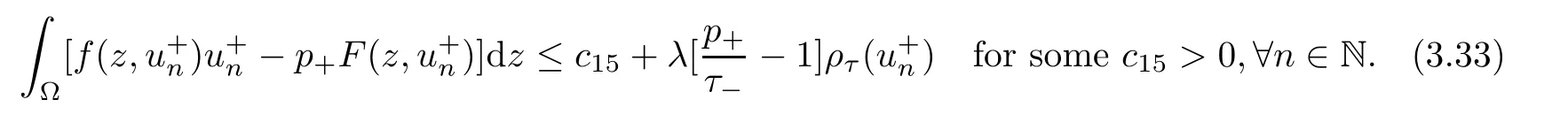
Hypotheses H2(i)，(iii) imply that we can find c16＞0 such that

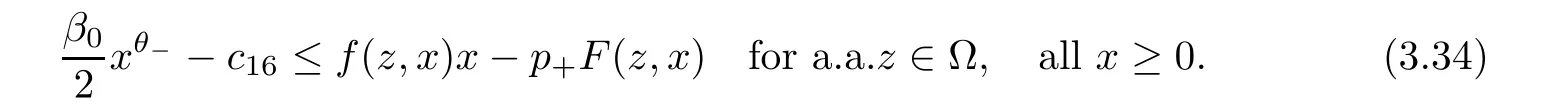
Using (3.34) in (3.33)，we obtain

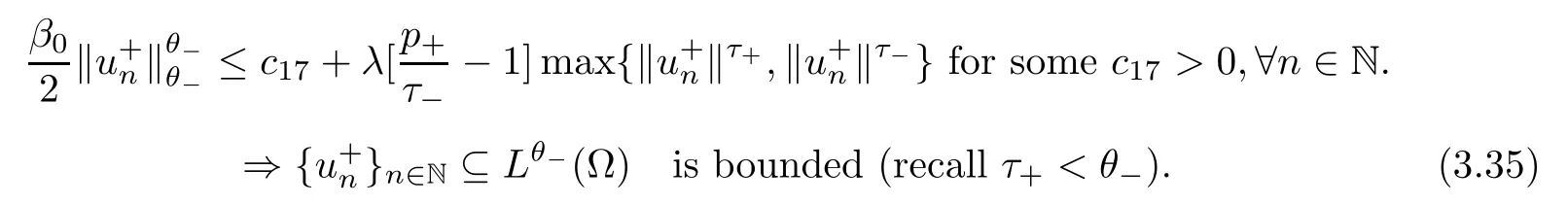
From hypothesis H2(iii)，we see that we may always assume that θ-＜r＜.Let t∈(0，1) such that

Invoking the interpolation inequality (see，for example，Papageorgiou-Winkert[30，p.116]，we have that

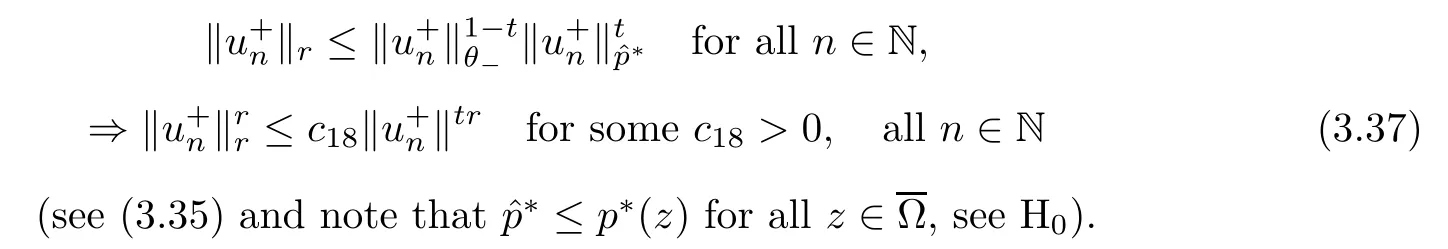
From hypothesis H2(i)，we have that

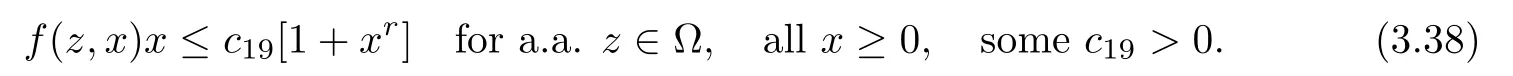
Since our goal is to show the boundedness of⊆W1，p (z)(Ω)，there is no loss of generality in assuming that≥1 for all n∈N.In (3.29) we choose h=∈W1，p (z)(Ω) and using (3.37)，(3.38)，(3.17) and Proposition 2.9，we have that

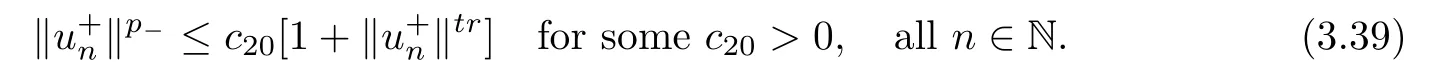
From (3.36) we have that

From (3.30) and (3.40) it follows that

{un}n≥1⊆W1，p (z)(Ω) is bounded，

so we may assume that

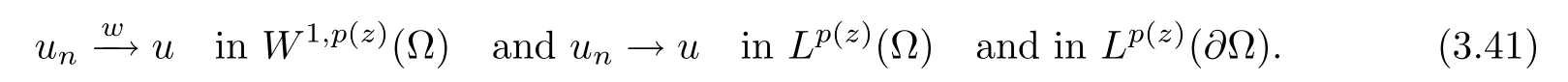
In (3.29) we choose h=un-u∈W1，p (z)(Ω)，pass to the limit as n→∞，and use (3.41).We obtain

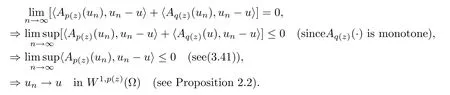
Therefore μλ(·) satisfies the C-condition.This proves the Claim.

Then (3.25)，(3.26) and the Claim permit the use of the mountain pass theorem.Thus，we can find∈W1，p (z)(Ω) such that

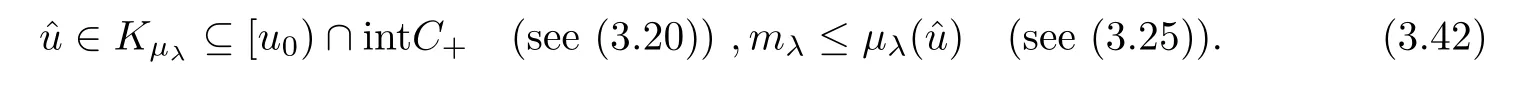
From (3.42)，(3.17) and (3.29)，we infer that

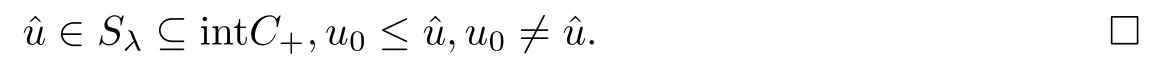
Finally，it remains to decide whether the critical parameter value λ*＞0 is admissible (that is，if λ*∈L).To do this，we need to do some preliminary work，which will also be useful in Section 4.

From hypotheses H2(i)，(iv)，we see that we can find c21＞0 such that

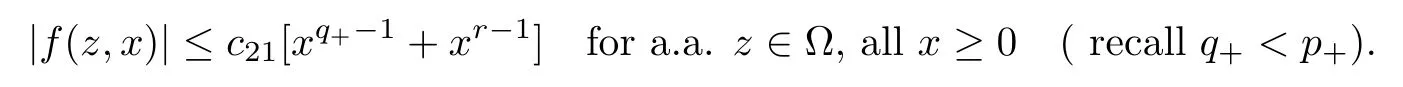
Therefore we have

Motivated by this unilateral growth estimate for the reaction of problem (pλ)，we consider the following auxliary anisotropic Robin problem:

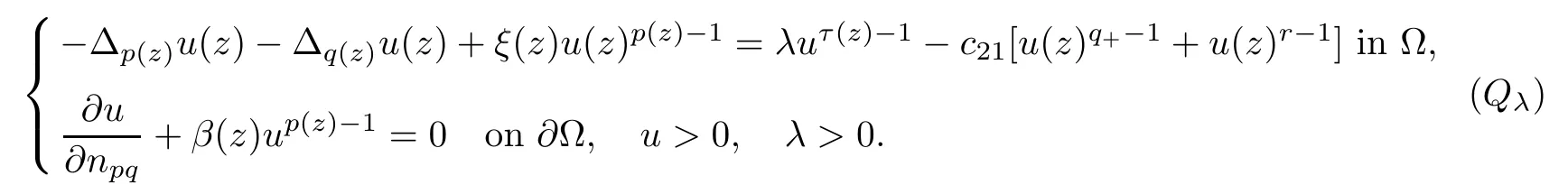
Proposition 3.6If hypotheses H0，H1hold and λ＞0，then problem (Qλ) admits a unique positive solution∈inf C+，and the map λ→frominto C+is nondecresing，that is，

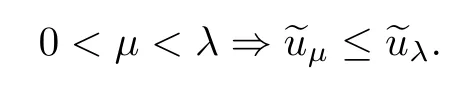
ProofFirst we show the existence of a positive solution for problem (Qλ).To this end，we consider the C1-functional ξλ:W1，p (z)(Ω)→R defined by

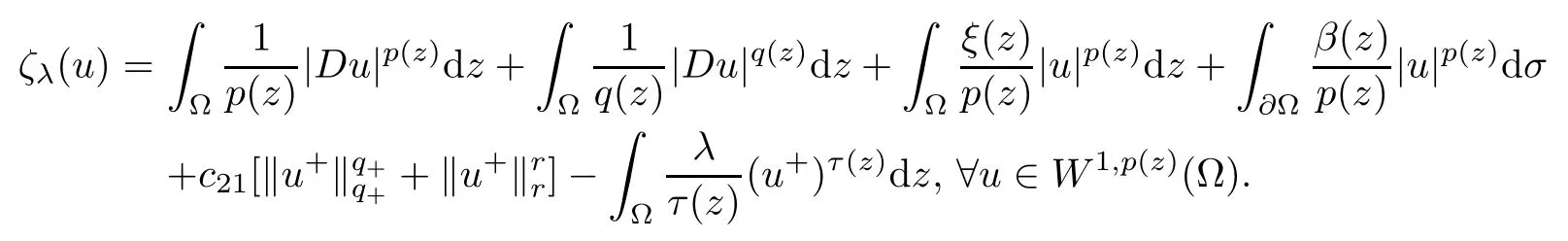
Since τ+＜q-≤q+＜p+，and using Proposition 2.9，we see that

ζλ(·) is coercive.

Also，ζλ(·) is sequentially weakly lower semicontinuous.Thus，we can find∈W1，p (z)(Ω) such that

In addition，the regularity theory and the maximum principle imply that

Using the integral functional j (·) from the proof of Proposition 3.1，we show，exactly as in that proof，that the positive solution∈intC+is unique.

Finally we show the monotonicity of the solution map λ→.

We set Bμ(z，x)=and consider the C1-functional dμ:W1，p (z)(Ω)→R defined by

Evidently，dμ(·) is coercive (see (3.44)) and sequentially weakly lower semicontinuous.Therefore，we can find∈W1，p (z)(Ω) such that

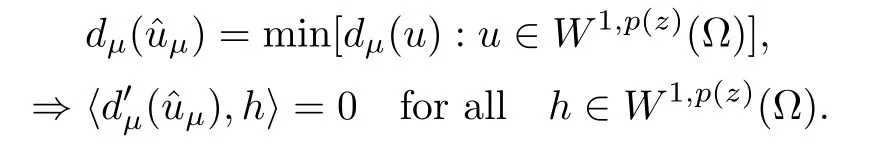
The unique positive solution∈intC+of (Qλ) provides a lower bound for the elements of Sλ.

Proposition 3.7If hypotheses H0，H1and H2hold and λ∈L，then

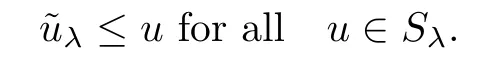
ProofLet u∈Sλ⊆intC+and consider the continuous on×R function wλ(z，x) defined by

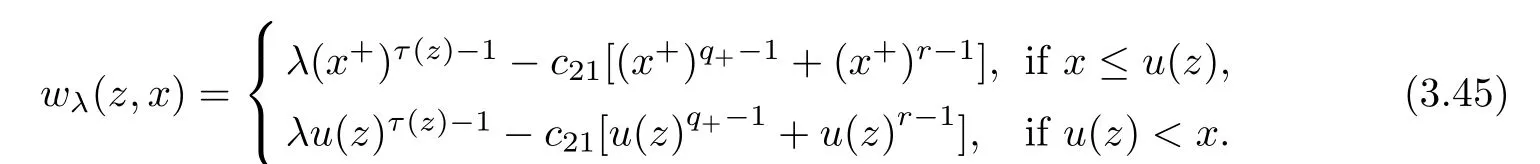
We set Wλ(z，x)=and consider the C1-functional iλ:W1，p (z)(Ω)→R defined by

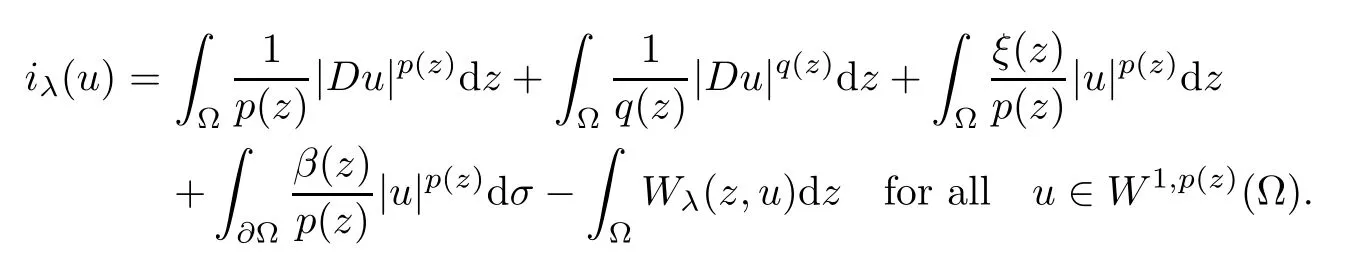
The functional is coercive and sequentially weakly lower semicontinuous，so we can find∈W1，p (z)(Ω) such that

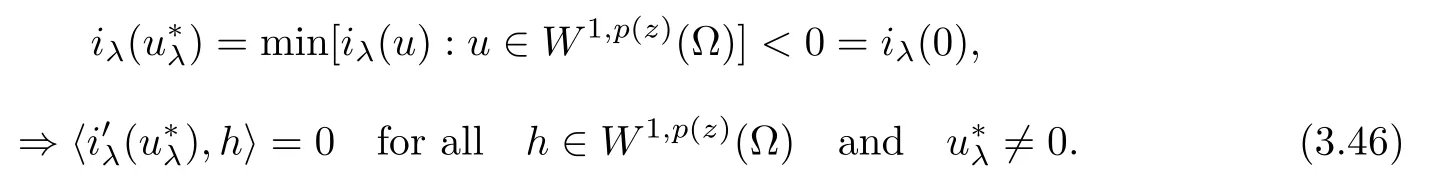
In (3.46)，first we choose h=∈W1，p (z)(Ω)，and using (3.45) we show that≥0，0.Next，in (3.46)，we choose h=∈W1，p (z)(Ω).Then

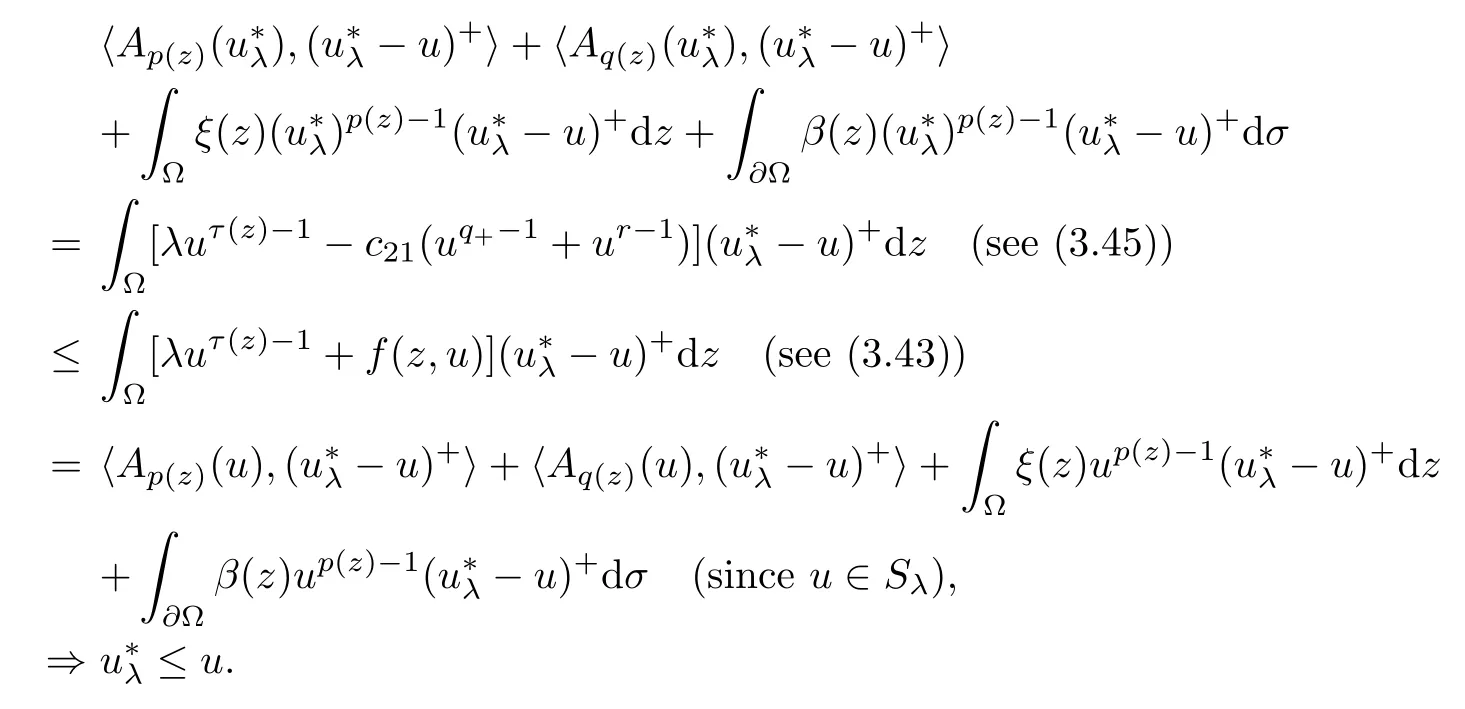
Thus，we have proved that

From (3.47)，(3.45) and (3.46)，we infer that

Now we are ready to prove the admissibility of the critical parameter λ*＞0.In what follows by φλ:W1，p (z)(Ω)→R，we denote the C1-energy functinonal of problem (pλ) defined by

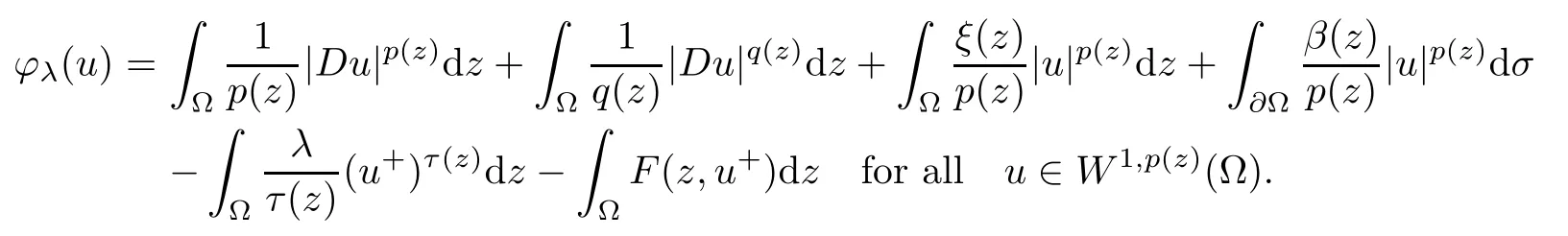
Proposition 3.8If hypotheses H0，H1and H2hold，then λ*∈L.

ProofLet λn∈(0，λ*)⊆L such that λn↑λ*and un∈⊆intC+，n∈N.From the proof of Proposition 3.2，we know that we can have

Using (3.48)(3.49)，and reasoning as in the Claim in the proof of Proposition 3.5，we obtain that

From (3.49)，in the limit as n→∞，we have that

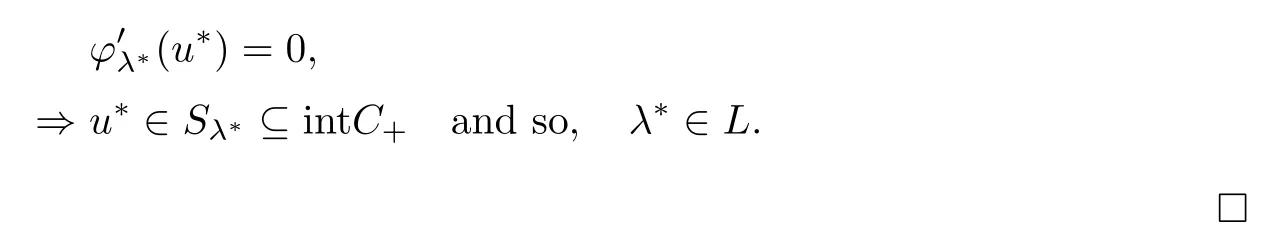
Therefore，we have established that

L=(0，λ*].

Summarizing our findings in this section，we can formulate the following bifurcation-type theorem，describing the dependence of the set of positive solutions on the parameter λ＞0:

Theorem 3.9If hypotheses H0，H1and H2hold，then there exists a critical parameter value λ*＞0 such that

(a) for every λ∈(0，λ*)，problem (pλ) has at least two positive solutions:

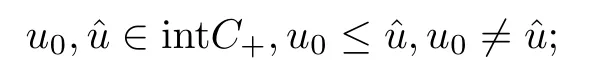
(b) for λ=λ*，problem (pλ) has at least one positive solution:

u*∈intC+;

(c) for every λ＞λ*，problem (pλ) has no positive solution.

Remark 3.10Note that in the multiplicity result (that is，for λ∈(0，λ*))，the two solutions are ordered.

4 Minimal Positive Solutions

In this section we show that for every λ∈L=(0，λ*]，problem (pλ) has a smallest positive solution∈intC+(minimal positive solution)，and we determine the monotonicity and continuity properties of the map L∋λ→uλ∈C+.

From Papageorgiou-Radulescu-Repovs[25](see the proof of Proposition 2.9)，we know that the set Sλis downward directed.

Proposition 4.1If hypotheses H0，H1，H2hold，and λ∈L=(0，λ*]，then the problem (pλ) has a smallest positive solution∈intC+.

ProofFrom Lemma 3.10 of Hu-Papageorgiou[15，p.178]，we know that we can find a decreasing sequence{un}n≥1⊆Sλsuch that

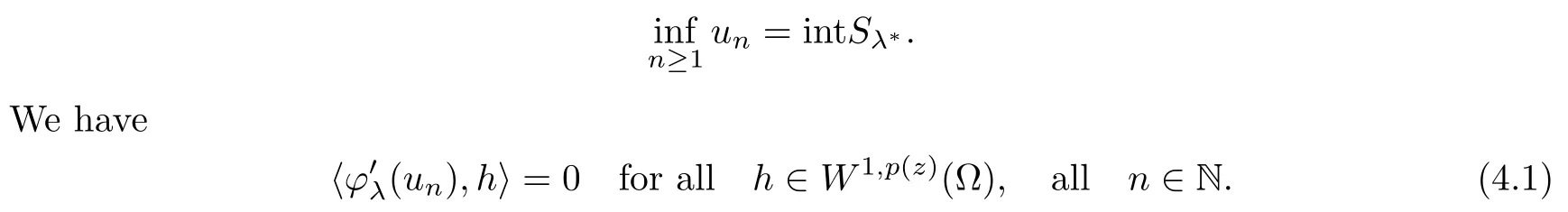
{un}n≥1⊆W1，p (z)(Ω) is bounded.

Thus we may assume that

In (4.1) we use that test function h=un-∈W1，p (z)(Ω)，pass to the limit as n→∞，and use (4.2).Then

Proposition 4.2If hypotheses H0，H1and H2hold，then the minimal solution map λ→from L=(0，λ*]intohas the following properties:

(a) it is strictly increasing，that is，if 0＜μ＜λ≤λ*，then

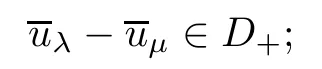
(b) it is left continuous.

Proof(a) Suppose that 0＜μ＜λ≤λ*.According to Proposition 3.3，we can find uμ∈Sμ⊆inf C+such that

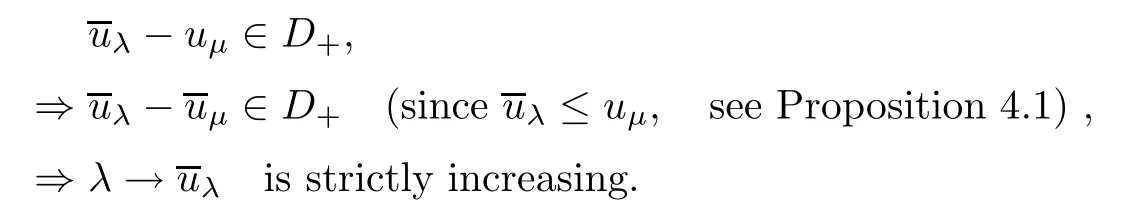
(b) Let λn→λ-with λn∈L for all n∈N.Then λ∈L，and we have that

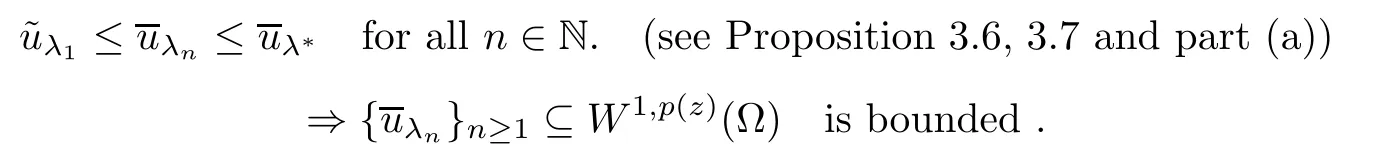
Then，from Fan-Zhao[11，Theorem 4.1](see also Gasinski-Papageorgiou[14，Proposition 3.3]and Tan-Fang[35，Theorem 3.1]，we have that

Then the anisotropic regularity theory (see Tan-Fang[35]) implies that there exist α∈(0，1) and c23＞0 such that

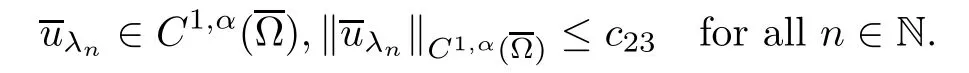
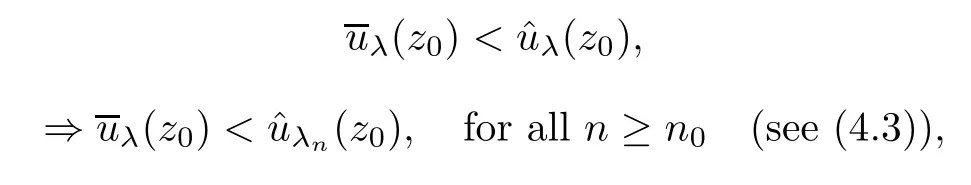
which contradicts (a).

Summarizing our findings in this section，we can state the following theorem:

Theorem 4.3If hypotheses H0，H1and H2hold，then for every λ∈L=(0，λ*]，problem (pλ) has a smallest positive solution∈intC+，and the map λ→from L intois strictly increasing in the sense that 0＜μ＜λ≤λ*⇒∈D+，and is left continuous.