FURTHER EXTENSIONS OF SOME TRUNCATED HECKE TYPE IDENTITIES*

Helen W.J.ZHANG (张文静)

School of Mathematics，Hunan University，Changsha 410082，China E-mail:helenzhang@hnu.edu.cn

Abstract The main purpose of this paper is to generalize the study of the Hecke-Rogers type series，which are the extensions of truncated theorems obtained by Andrews，Merca，Wang and Yee.Our proofs rely heavily on the theory of Bailey pairs.

Key words theta functions;truncated series;Bailey pair;Bailey transform

1 Introduction

Here and throughout this paper，we adopt the following common notation:

where a and q are complex numbers with|q|＜1.

Andrews and Merca in[3]proved the following truncated theorem on Euler’s identity:for m≥1，

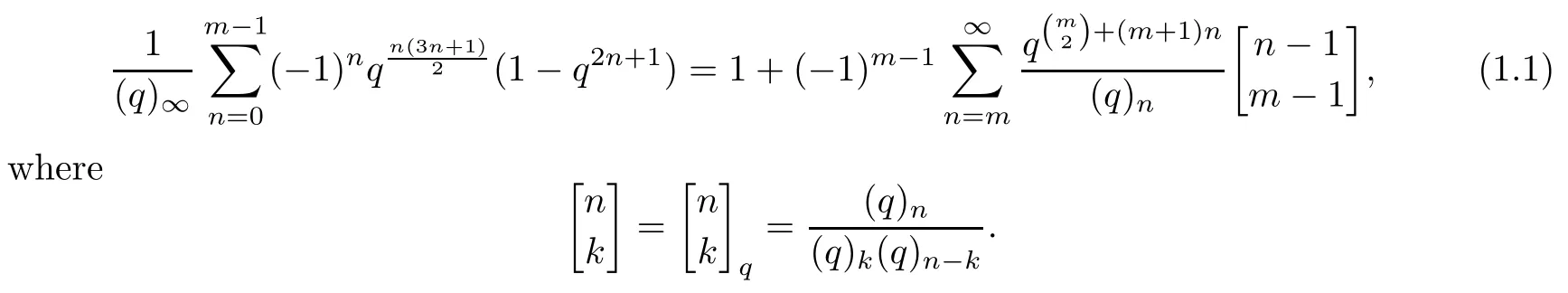
Recall that a partition of a positive integer n is a finite nonincreasing sequence of positive integers λ1，λ2，···，λrsuch thatP=n.The function p (n) is the number of partitions of n.Andrews and Merca also proved that，for N，m≥1，

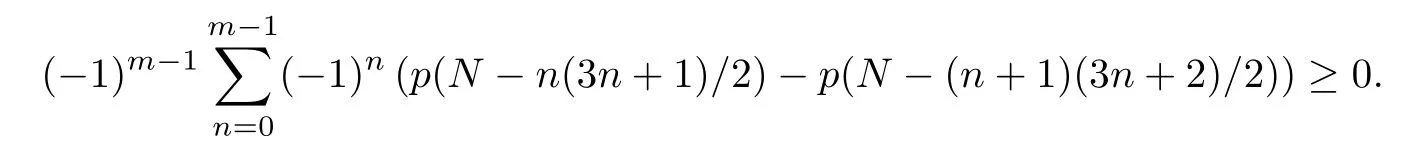
Guo and Zeng in[9]showed truncated theorems on the following well-known identities of Gauss[1]:

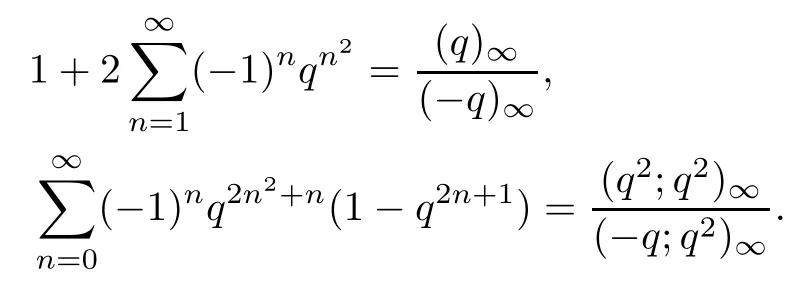
Recall that an overpartition of n is a partition of n in which the first occurrence of a number can be overlined.Letdenote the number of overpartitions of n and let pod (n) denote the number of partitions of n wherein odd parts are distinct.Guo and Zeng mentioned that for N，m≥1，

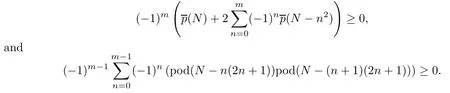
Quite recently，Wang and Yee[14]reproved the results of Guo and Zeng.To be more specific，for m≥0，

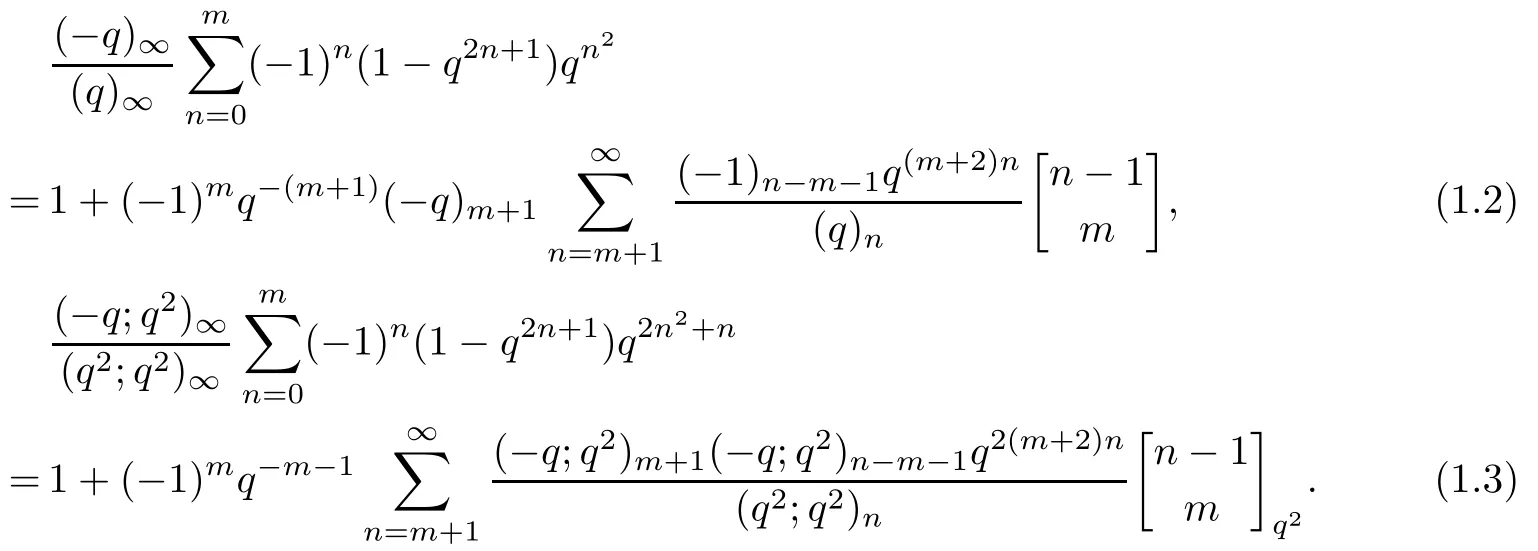
Moreover，Wang and Yee[14]also mentioned the following truncated Hecke-Rogers type double series:

Since then，there has been a great deal of work on truncated series，see，for example，[4，6，7，15].

In this paper，motivated by the works of Andrews and Merca[3]，Guo and Zeng[9]，and Wang and Yee[14]，we study extensions of the truncated theorems (1.1)-(1.6).

Theorem 1.1We have

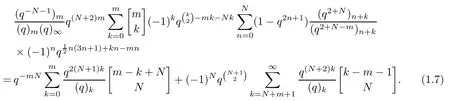
Theorem 1.2We have

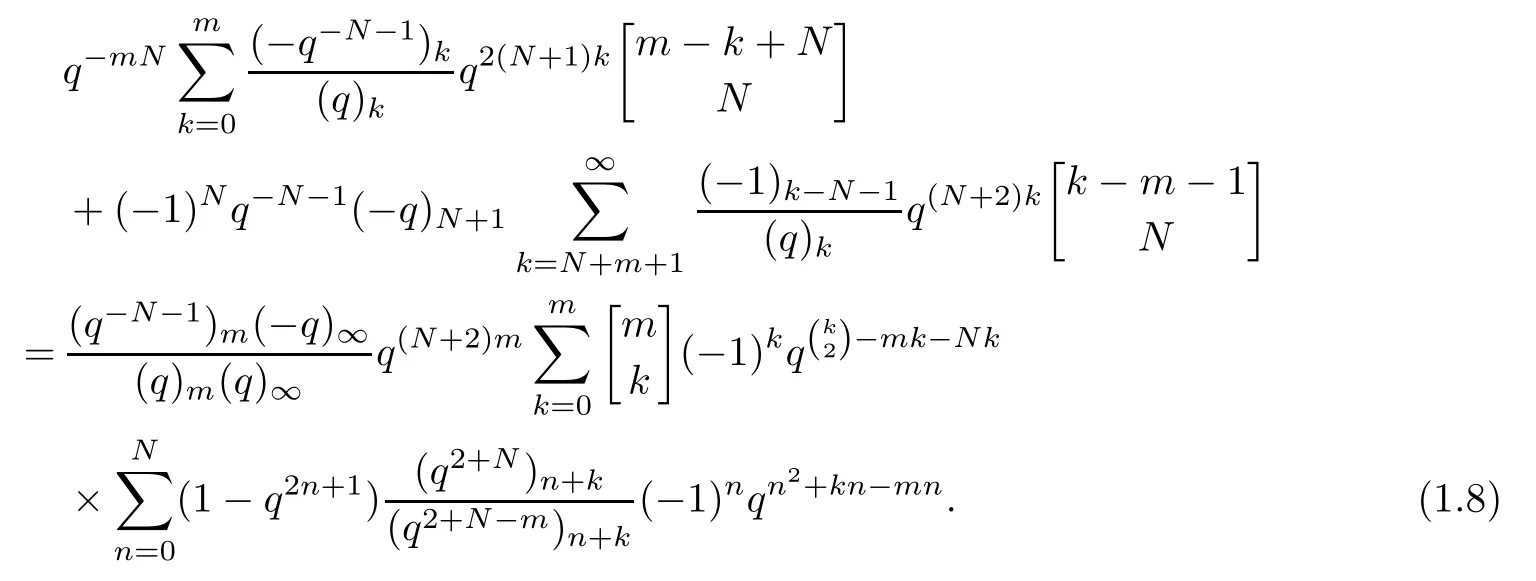
Theorem 1.3We have

Theorem 1.4We have

Theorem 1.5We have

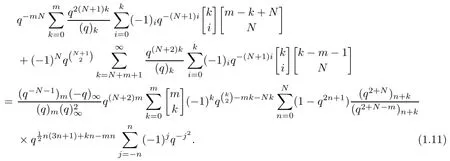
Theorem 1.6We have

Remark 1.7Equations (1.1)-(1.6) can be obtained by setting m=0 in Theorems 1.1-1.6，respectively.

The approaches in the papers dealing with these themes are similar:they proceed by choosing different complex sequences in certain q-hypergeometric transformations.However，Wang and Yee directly utilized a transform due to Z.-G.Liu，while we show a new transform using Bailey pairs so that Liu’s transform is indeed generalized.

This paper is organized as follows:in Section 2，we state the general transformation formula for the q-series，which plays a key role in the proofs of the main theorems.We then establish several truncated Hecke-Rogers type series by choosing different Anin the transformation formula in Section 3.Moreover，extensions of the truncated theorems of Andrews-Merca and Guo-Zeng are discussed.Finally，in Section 4，we display several truncated Hecke-Rogers type double series.

2 Preliminaries

In this section，we use a Bailey pair to set up the general transformation formula for the q-series.We now recall the following lemma，which is due to[13]:

Lemma 2.1Let m be a nonnegative integer.Then，for|c/ab|＜1，we have

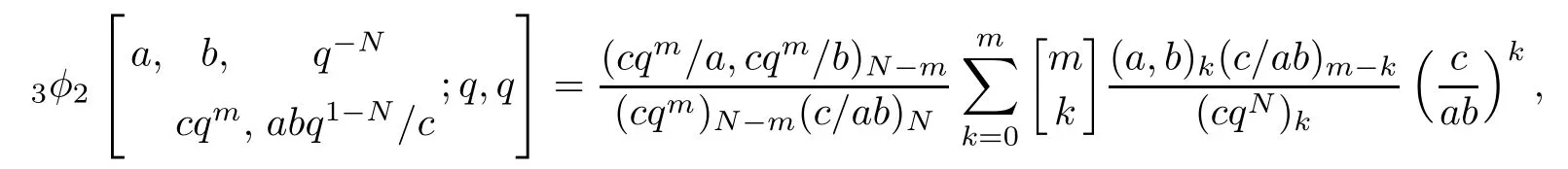
where

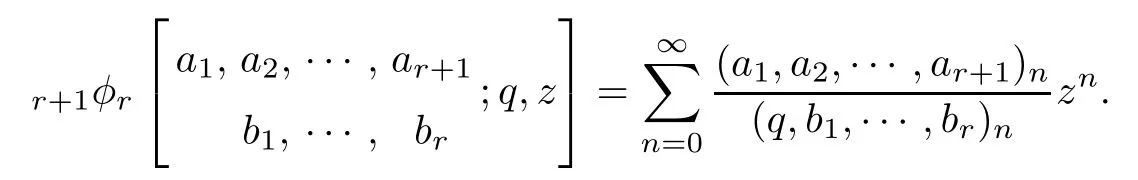
Recall that (αn，βn) is said to be a Bailey pair relative to a if

Moreover，if only the βnis given，then αncan be determined using Bailey inversion (see[2]) as follows:

The pair (γn，δn) is said to be a conjugate Bailey pair with respect to a if the two sequences satisfy (see[5])

Then，under suitable convergence conditions，

where αnand δnare arbitrarily chosen sequences of n alone.For more details we refer to the reviews[16].

Theorem 2.2Let m be a nonnegative integer.If{An}is a complex sequence，then under suitable convergence conditions，we have

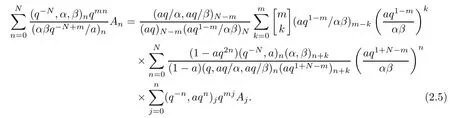
ProofIn (2.3)，setting

we have

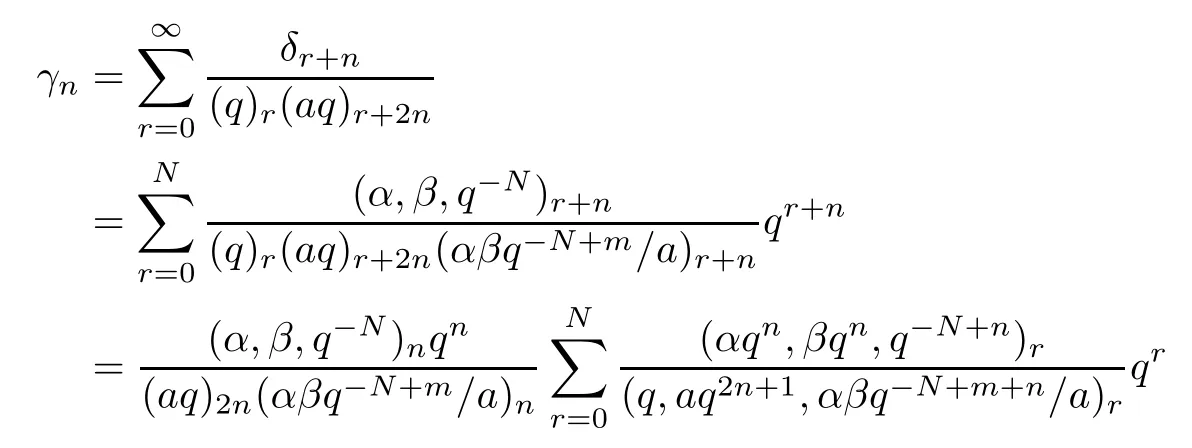
Replacing a，b and c by αqn，βqnand aq2n+1-min Lemma 2.1，respectively，we obtain

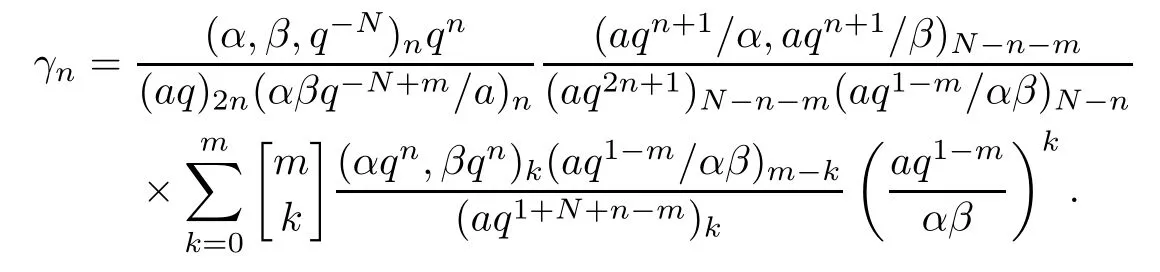
Substituting this into (2.4)，we have

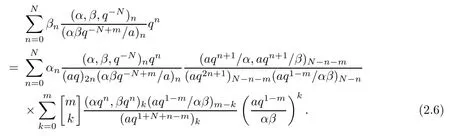
De fine α(a，n) to be

Hence，(α(a，n)，q(m-1) nAn/(α，β)n) forms a Bailey pair.Inserting this Bailey pair into (2.6) yields

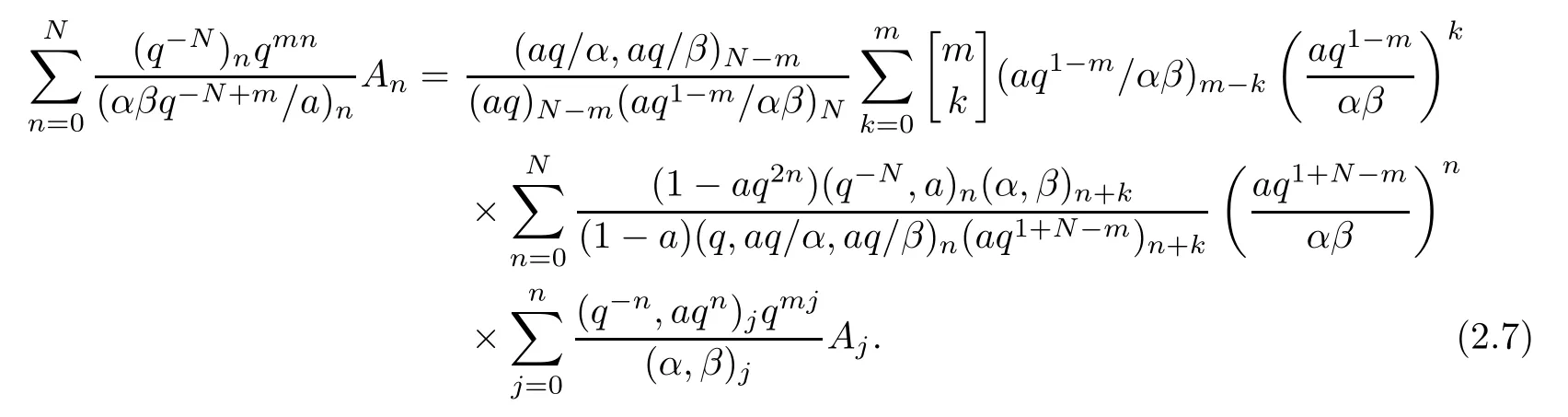
Replacing Ajby (α，β)jAj，we prove the theorem.

Remark 2.3When m=0，Theorem 2.2 becomes Theorem 9.2 in[12].

In the next lemma，a special case of Theorem 2.2 will be treated.

Lemma 2.4We have

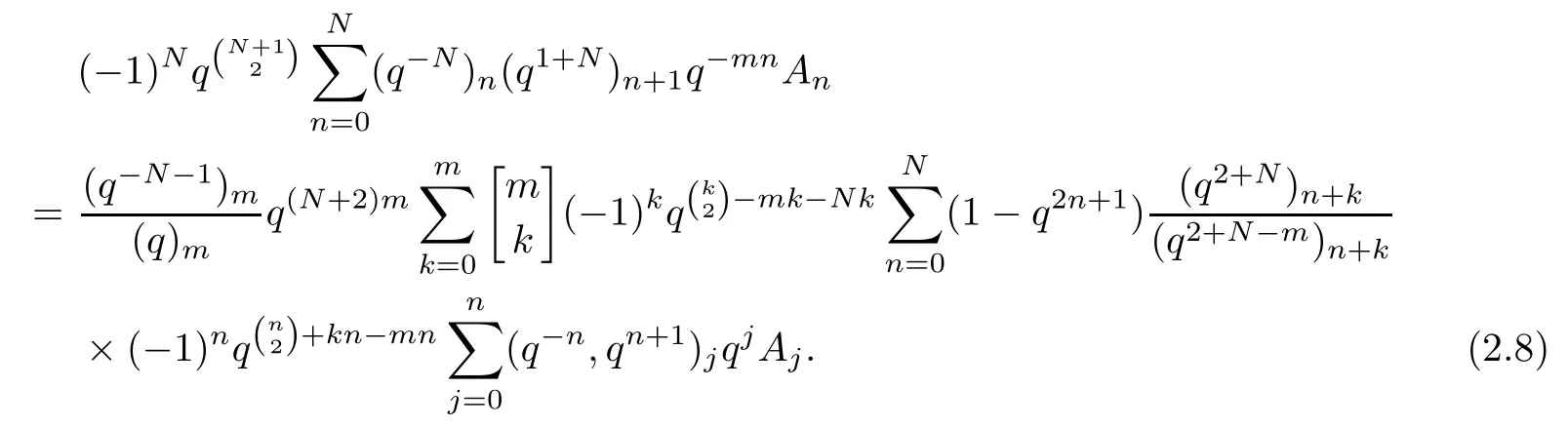
ProofTaking α→q1+Na in Theorem 2.2，then letting a→q and β→∞，we have

Employing the identity

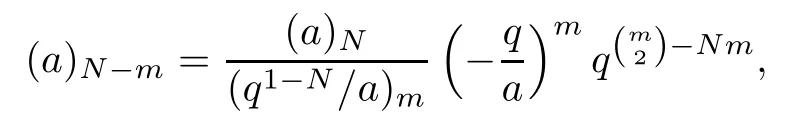
we infer that

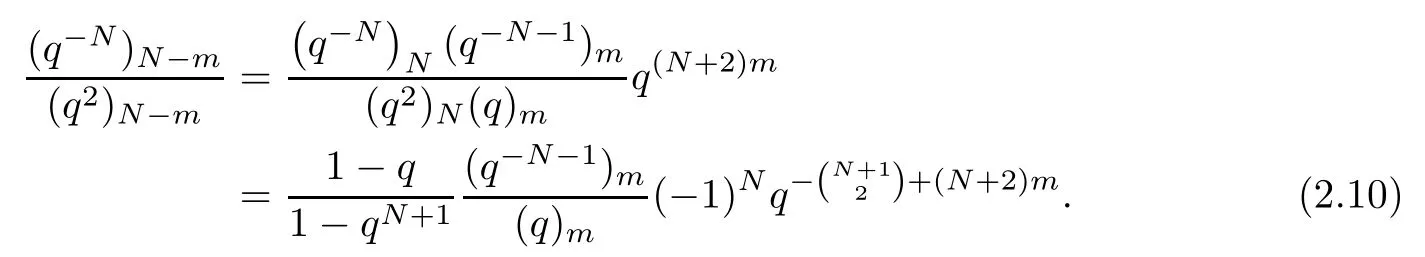
Plugging (2.10) into (2.9)，and replacing Anby q-mn+nAn，we complete the proof.

3 Truncated Hecke-Rogers Type Series

In this section，we prove Theorems 1.1，1.2 and 1.3.

Proposition 3.1We have

ProofReplacing Anbyin Lemma 2.4，we get

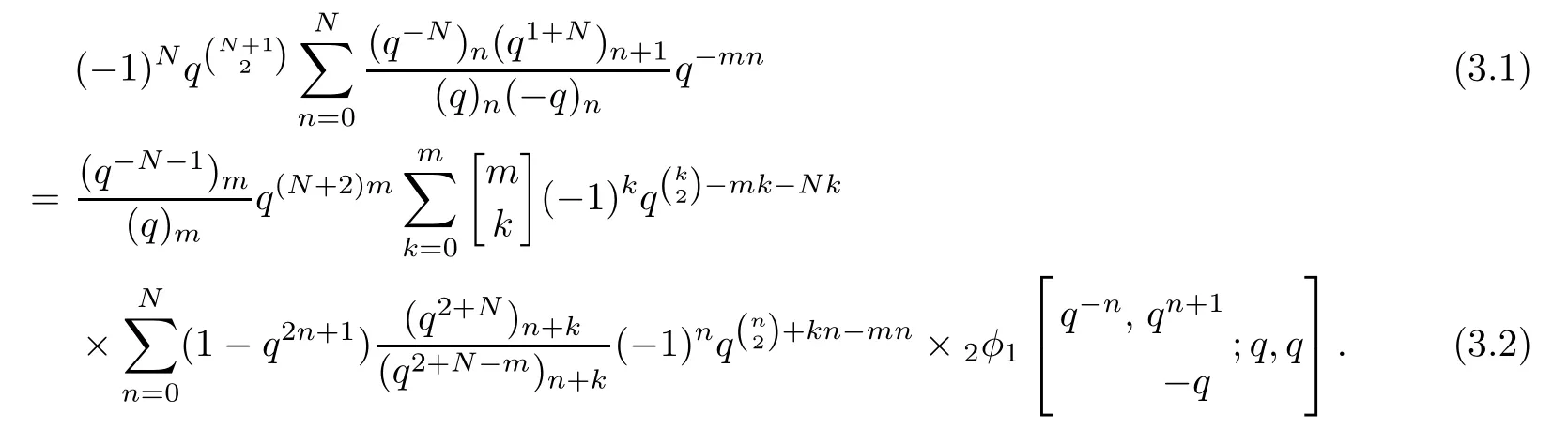
Employing the q-Vandermonde summation formula in[8]，that is，

we infer that

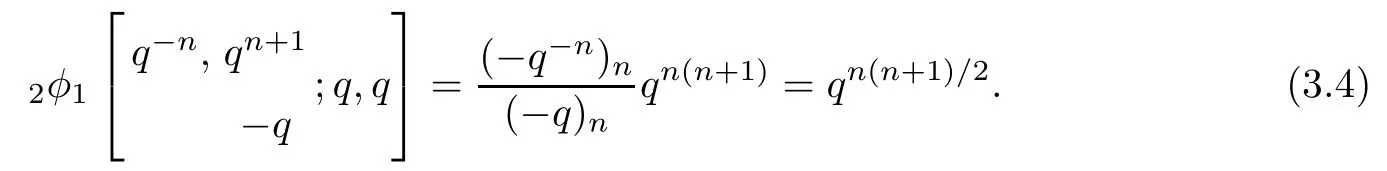
The proof can be completed by substituting (3.4) into (3.1).

3.1 Proof of Theorem 1.1

Taking An=1/(q)nin Lemma 2.4，we have

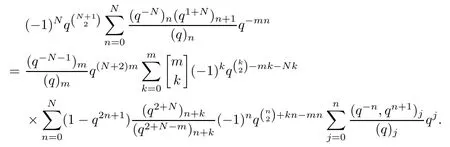
Applying the following identity in[11，Lemma 4.1]:

3. Fountain: In some versions of the story, the fountain is a well. Traditionally, good spirits live in wells, and from thence came the tradition of throwing coins into wells in hopes of having a wish come true (Philip 1997).Return to place in story.

we infer that

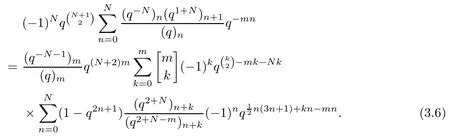
Multiplying both sides of (3.6) by，we have

Denote the term on the left-hand side of the above equation by L1.Then we obtain that

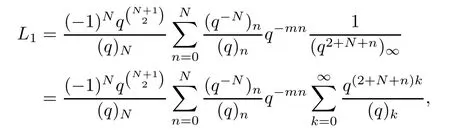
where for the last equality，we apply the equation

Then，we have

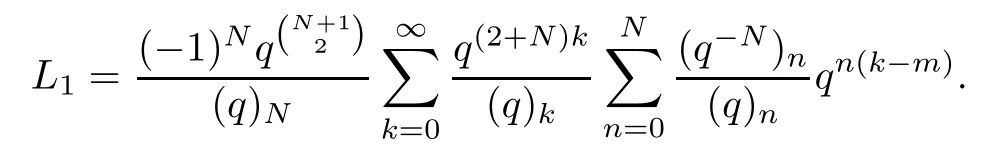
Substituting z by qk-min the following identity from[8]:

we have

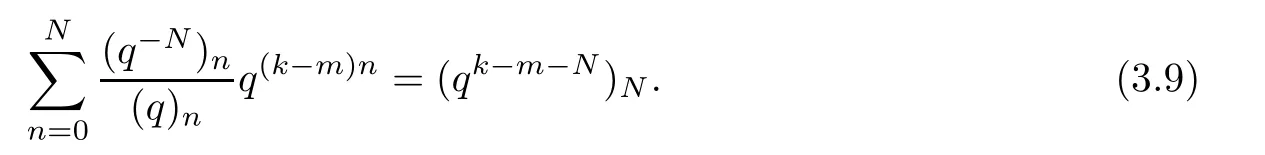
Then，L1can be rewritten as

Since

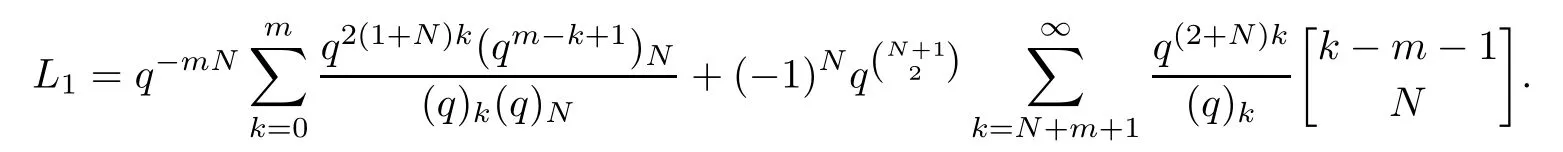
This completes the proof of Theorem 1.1.

The following corollary can be deduced by setting m=1 in Theorem 1.1:

Corollary 3.2We have

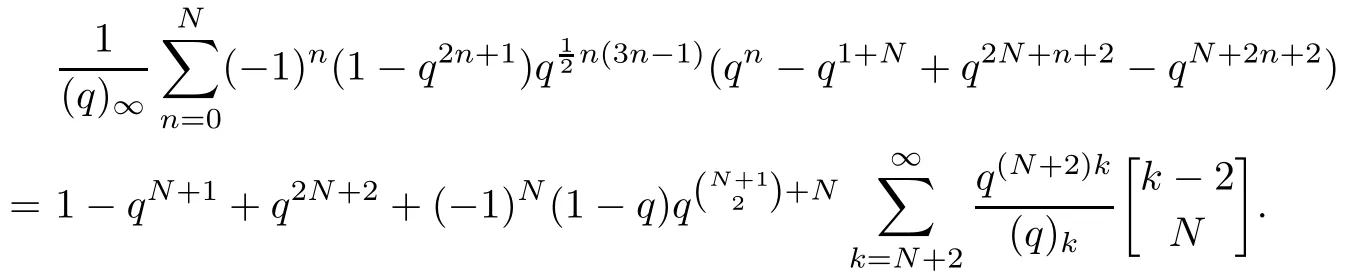
3.2 Proof of Theorem 1.2

Multiplying both sides of Proposition 3.1 by (-q)∞/(q)∞，we have

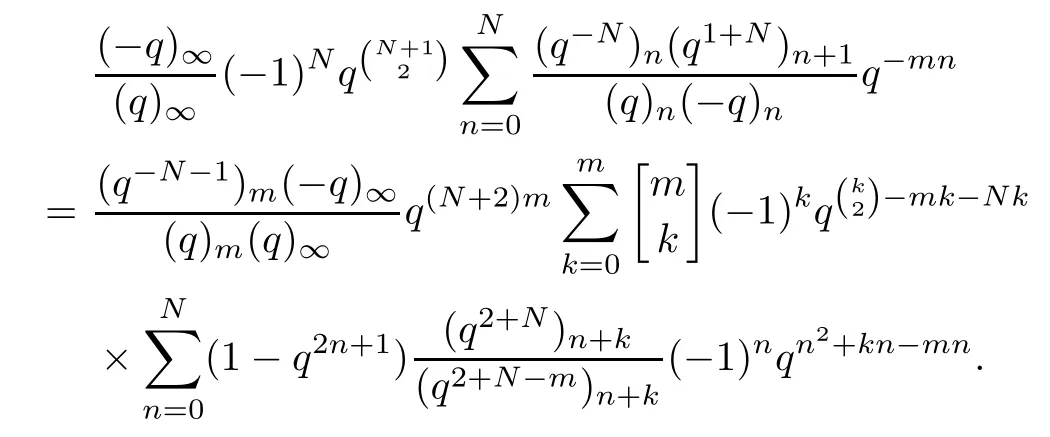
Denote the term on the left-hand side of the above equation by L2.Then we obtain that

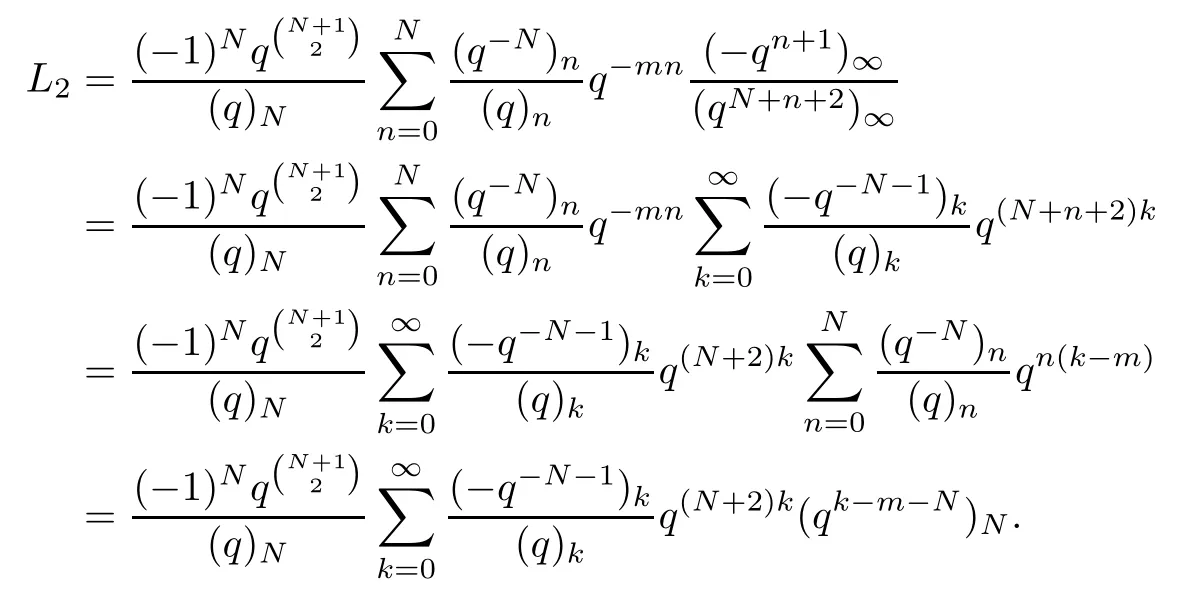
By (3.10)，L2is equal to

This completes the proof of Theorem 1.2.

Taking m=1 in Theorem 1.2，we obtain the following equation:

Corollary 3.3We have

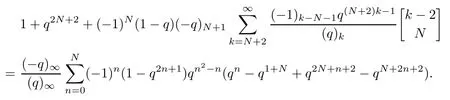
3.3 Proof of Theorem 1.3

In Lemma 2.4，replacing q by q2，then taking

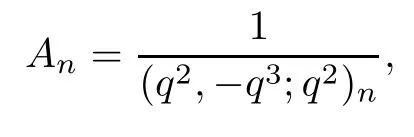
we obtain

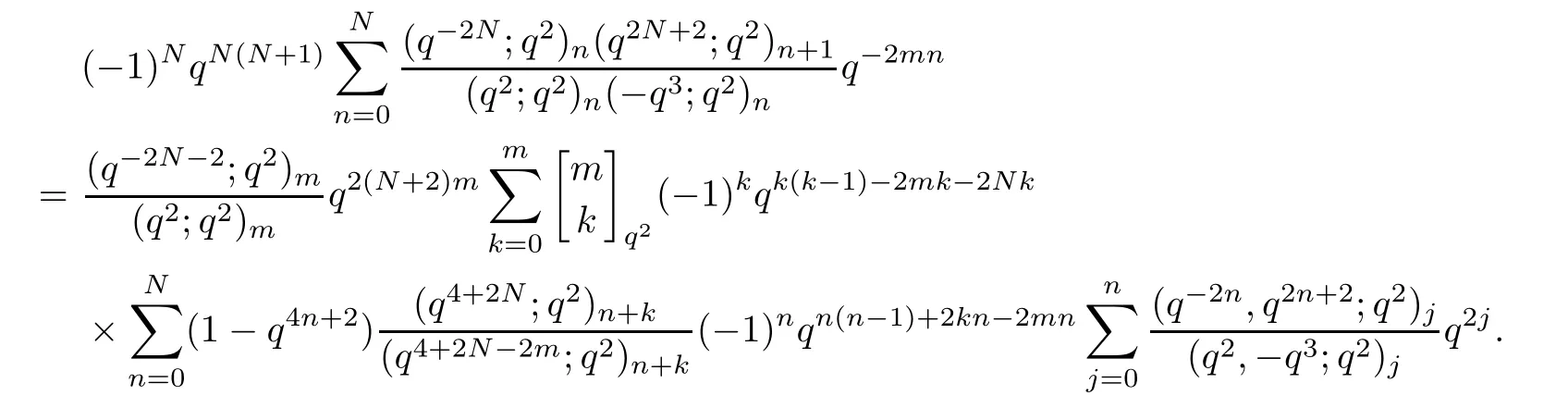
By (3.3)，

so we have

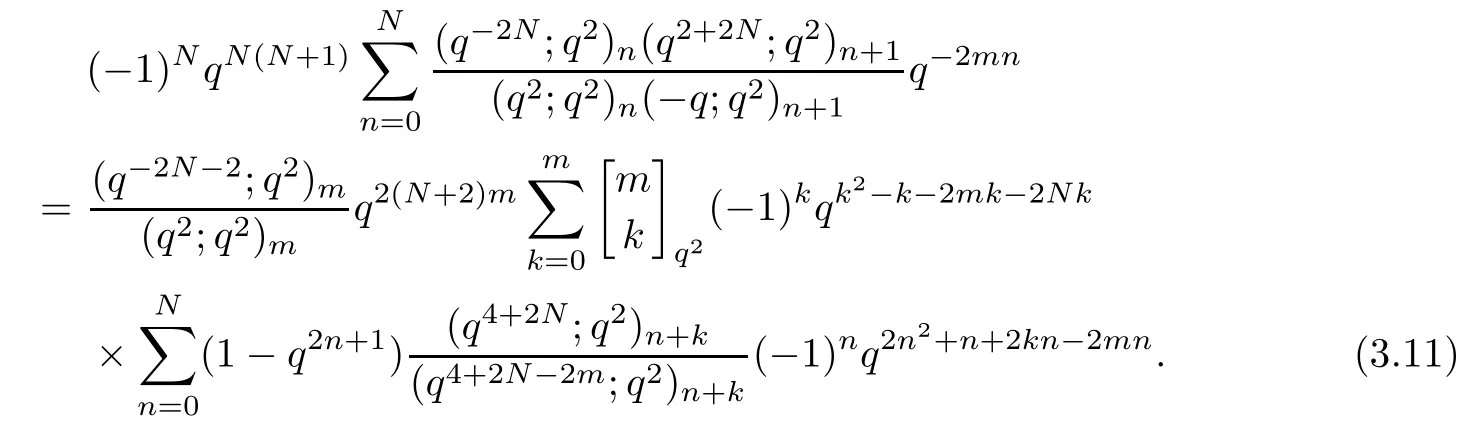
Multiplying both sides of (3.11) by (-q;q2)∞/(q2;q2)∞，we get

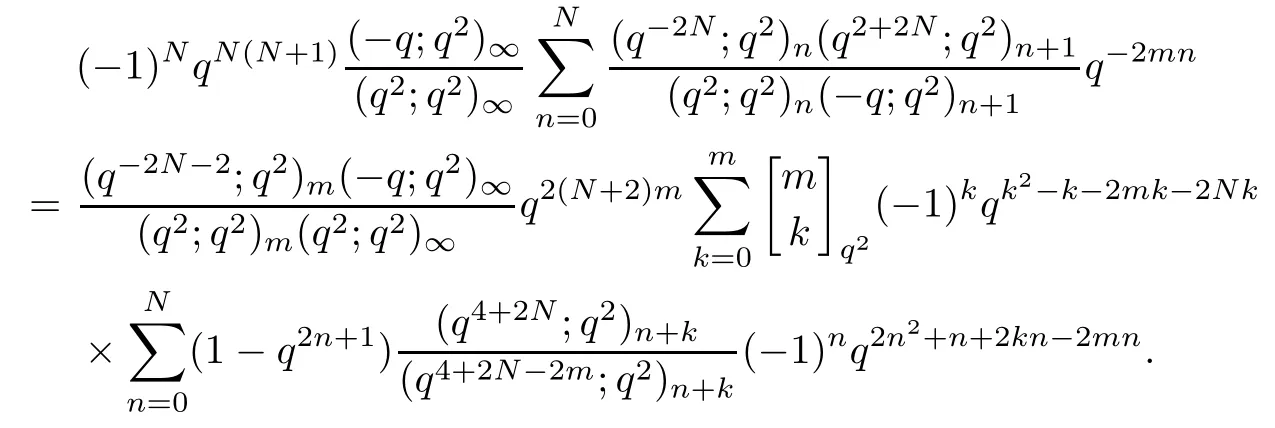
Denote the term on the left-hand side of above equation by L3.Then we obtain that

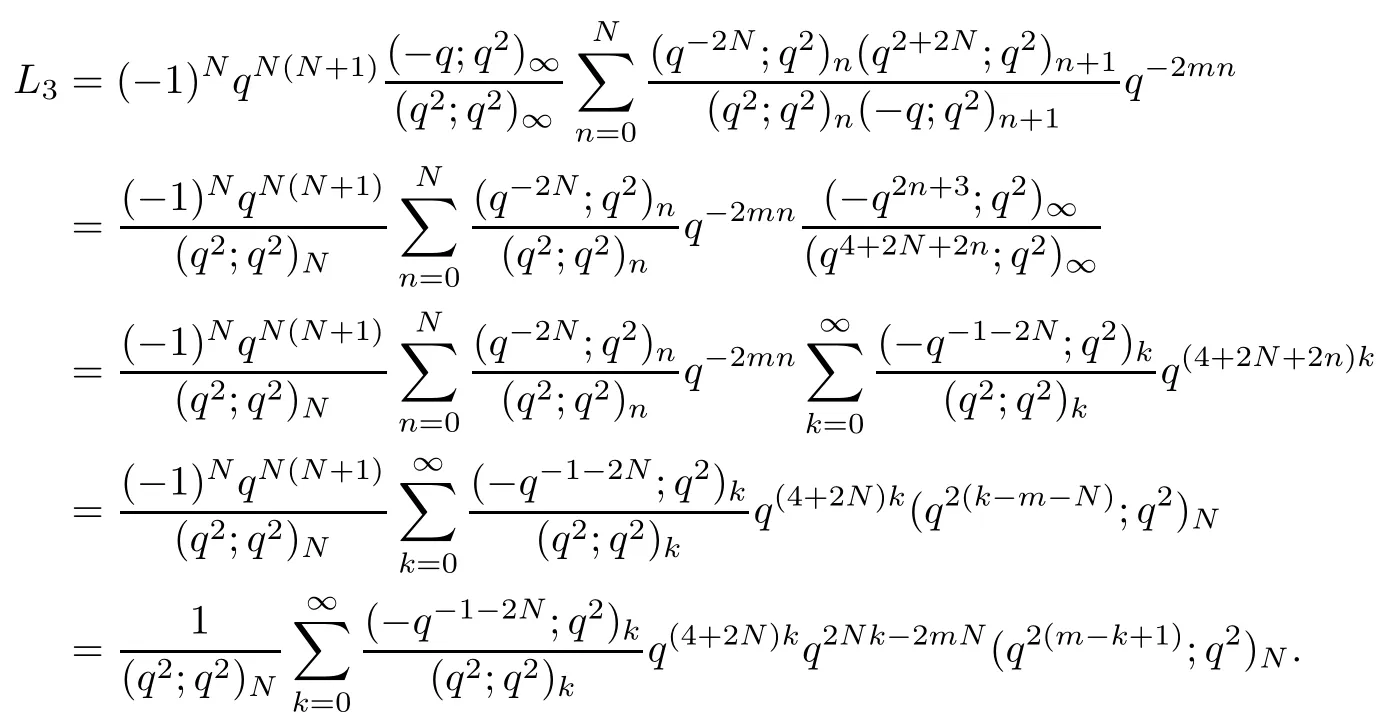
Splitting the summation of k into two sums，we have

This completes the proof of Theorem 1.3.

Taking m=1 in Theorem 1.3，we have the following corollary:

Corollary 3.4We have

4 Truncated Hecke-Rogers Type Double Series

In this section，we provide several truncated Hecke-Rogers type identities by taking different An’s in Lemma 2.4.

Proposition 4.1We have

ProofTaking An=1/(cq)nin Lemma 2.4，we get

Applying (3.5) with a=q in the above identity，we derive (4.1)，which completes the proof.

4.1 Proof of Theorem 1.4

Setting c→0 in (4.1) and multiplying both sides by，we have

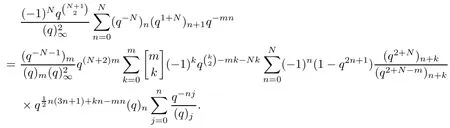
Using the following identity from[10，(7.10)]:

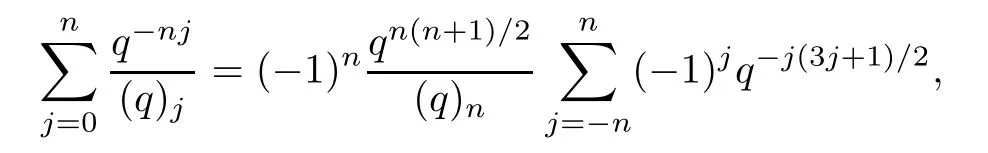
we arrive at

Denote the term on the left-hand side of (4.2) by L4.Then it can be rewritten as

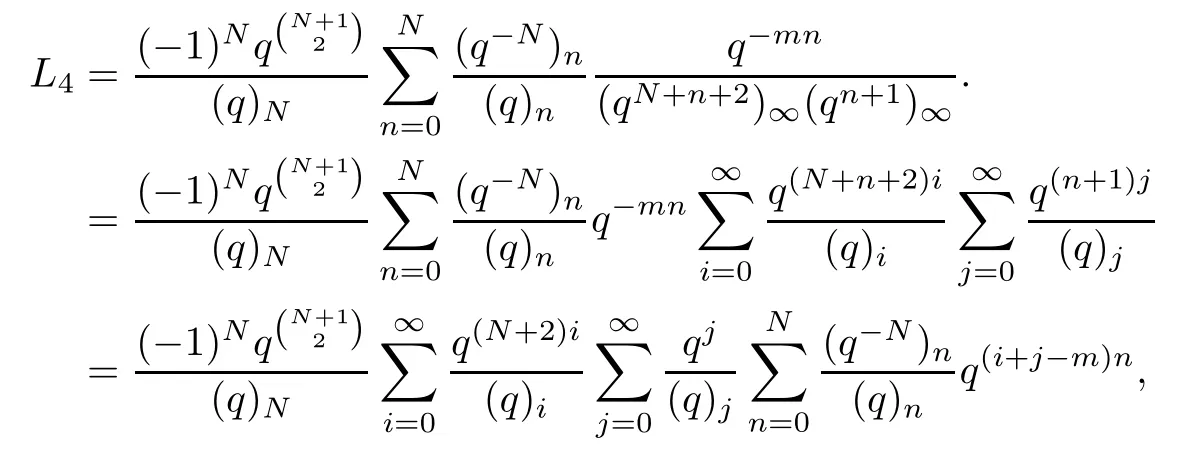
where the penultimate equality is due to (3.7).

Using (3.8)，we have

Splitting the above summation of k into two sums yields

Substituting the above equation into (4.2)，we finish the proof of Theorem 1.4.

The following is a special case of Theorem 1.4 by taking m=1:

Corollary 4.2We have

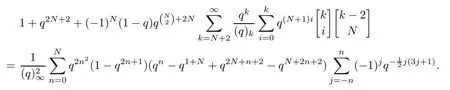
4.2 Proof of Theorem 1.5

Replacing c by-1 in (4.1)，multiplying both sides by，and applying the following identity from[10，(7.5)]:

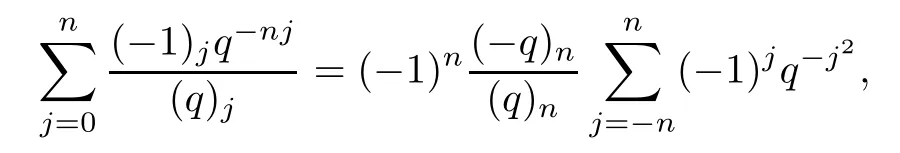
we deduce that

Denote the term on the left-hand side of (4.3) by L5.Then the calculations of L5are similar to those of L4in Theorem 1.4;that is，

Similarly，splitting the summation of k into two sums，we have

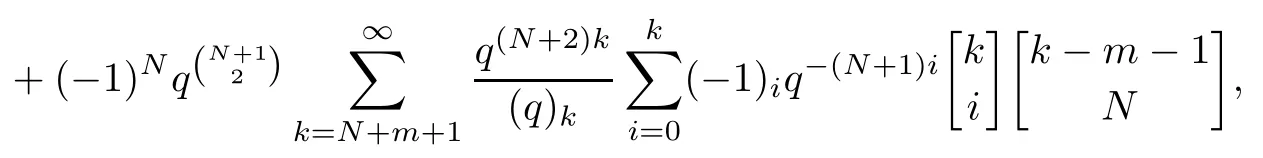
as desired.This completes the proof of Theorem 1.5.

The following is a direct consequence of Theorem 1.5，and it achieved by setting m=1:

Corollary 4.3We have

4.3 Proof of Theorem 1.6

Setting q→-q in the following equation from[10，(7.15)]:

we infer that

Replacing q and c by q2and-q in (4.1)，respectively，and applying (4.4)，we obtain

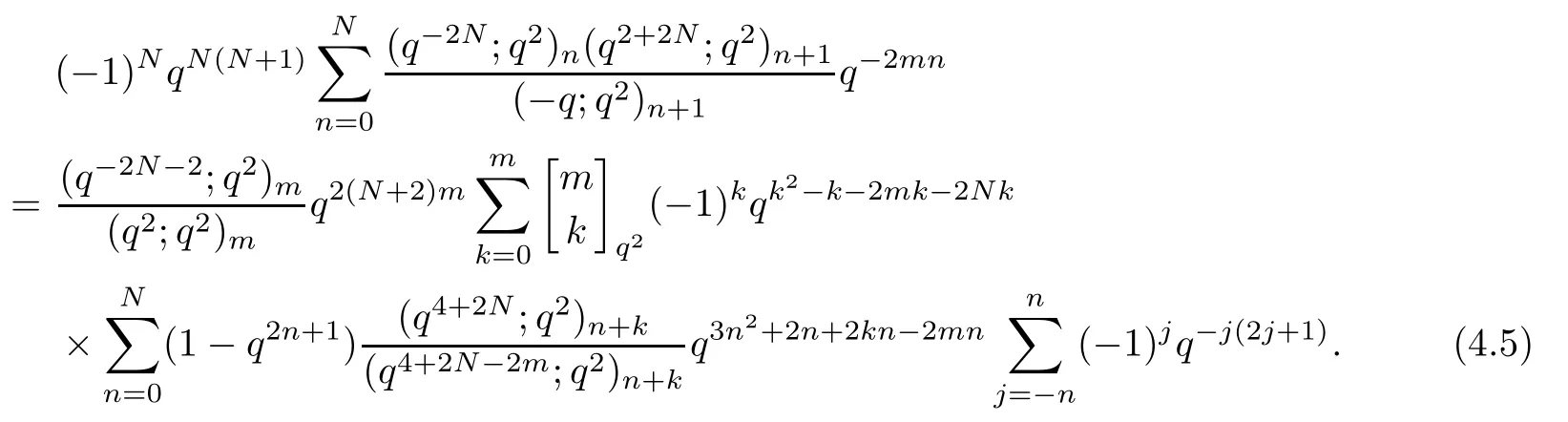
Multiplying both sides of (4.5) by (-q;q2)∞/，we obtain

Denote the term on the left-hand side of the above equation by L6.Then we have

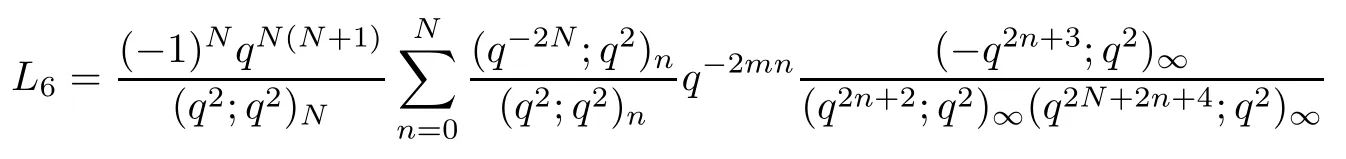
Splitting the summation of k into two sums，we arrive at

as desired.This completes the proof of Theorem 1.6.

Replacing m by 1 in Theorem 1.6，we obtain the following corollary:

Corollary 4.4We have

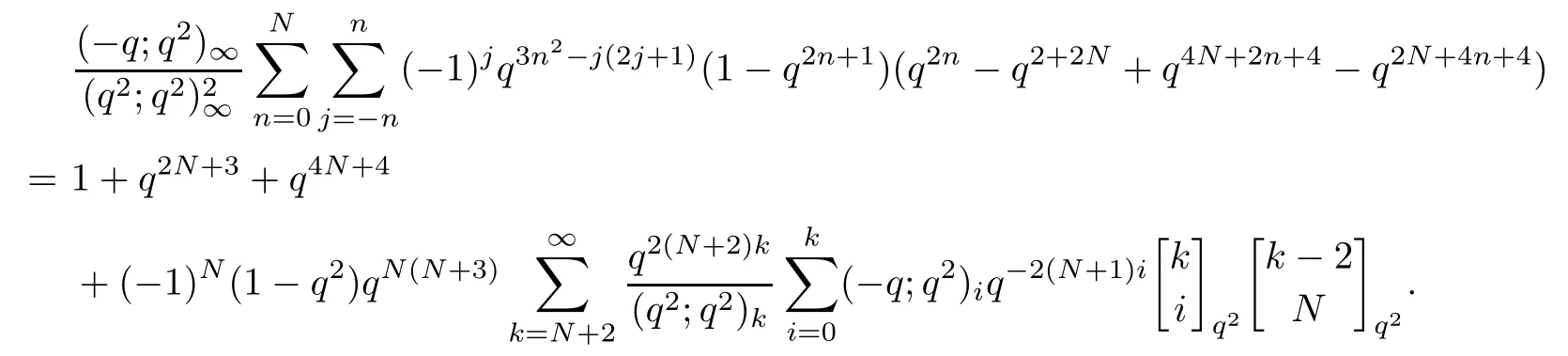
4.4 Truncated theorem on cubic partitions

We present another instance of truncated series identities which is related to the extension of the truncated series of (q)∞(q2;q2)∞.

Theorem 4.5We have

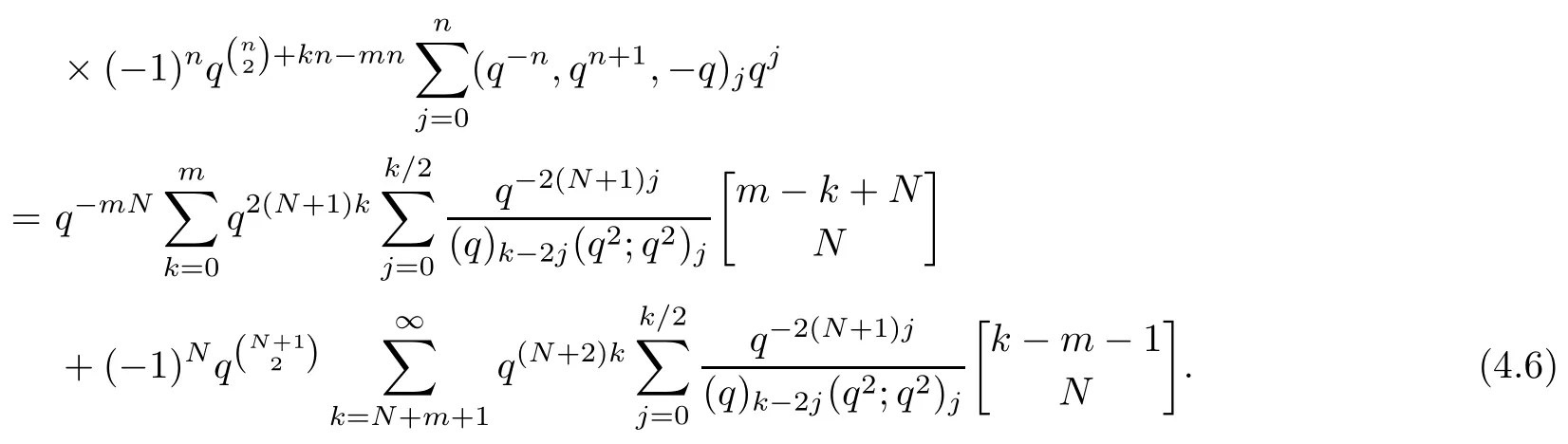
ProofTaking An=(-q)nin Lemma 2.4 and multiplying both sides by，we have

Denote the term on the left-hand side of the above equation by L7.Then we infer that

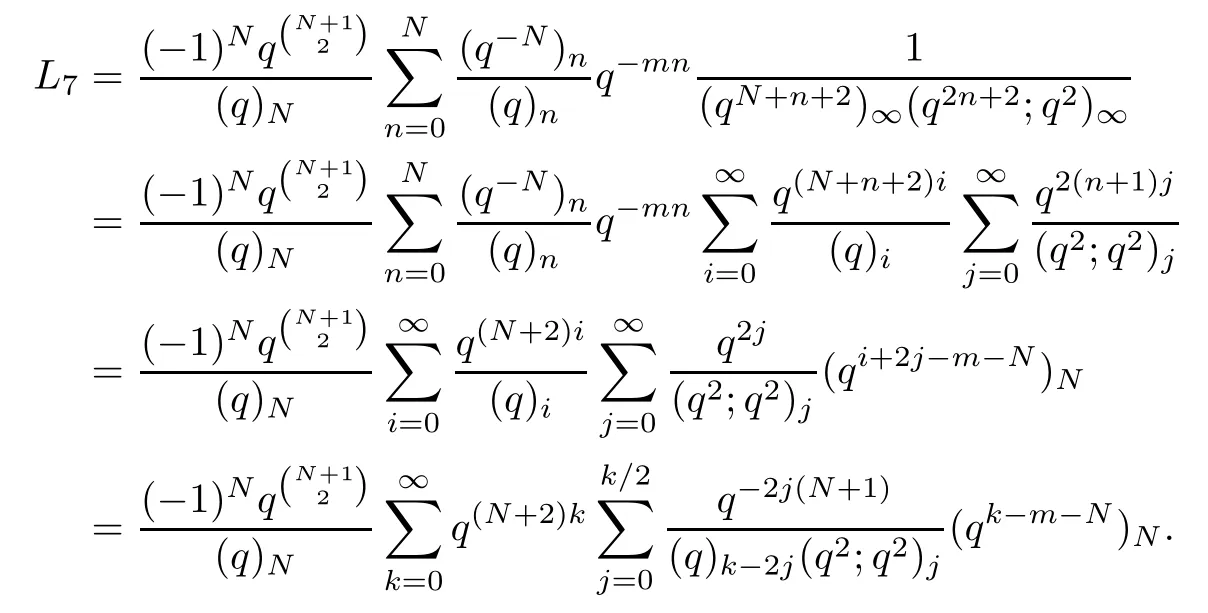
Splitting the summation of k into two sums as usual，we get that

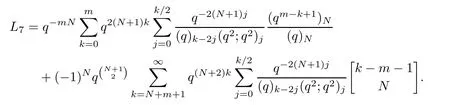
This completes the proof.

Taking m=0，1 in Theorem 4.5，we obtain the following results:

Corollary 4.6We have

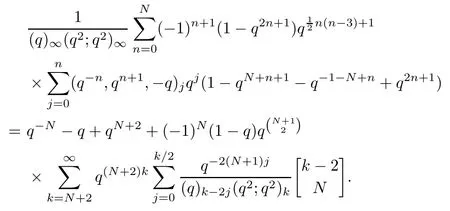
Remark 4.7The equation (4.8) is equivalent to Theorem 5.3 in[14].

We end this article with the following question arising from this project:

Question 4.8Can one give the combinatorial interpretations of Theorems 1.1-1.6?